Atkinson K. An Introduction to Numerical Analysis
Подождите немного. Документ загружается.


AITKEN EXTRAPOLATION FOR LINEARLY CONVERGENT SEQUENCES
85
Table
2.8
Iteration (2.6.6)
Estimate
n
xn
Xn-
Xn-I
An
a -
Xn
(2.6.5)
0 6.0000000
1.55E-
2
1
6.0005845
5.845E-
4
1.49E-
2
2
6.0011458
5.613E-
4
.9603
1.44E-
2
1.36E-
2
3
6.0016848
5.390E-
4
.9604
1.38E-
2
1.31E-
2
4
6.0022026
5.178E-
4
.9606
1.33E-
2
L26E-
2
5
6.0027001
4.974E-
4
.9607
1.28E-
2
1.22E-
2
6
6.0031780
4.780E-
4
.9609
1.23E-
2
1.17E-
2
7
6.0036374
4.593E-
4
.9610
USE-
2
1.13E-
2
Example
Consider the iteration
Xn+l
= 6.28 + sin
(xn)
n~O
(2.6.6)"
The true root
is
a
~
6.01550307297. The results of the iteration are given in
Table
2.8, along-with the-values of
An,
a-
xn,
xn
-
xn-l•
and the error estimate
(2.6.5). The values of
An
are converging to
g'( a)
=cos
(a)
~
.9644
and the estimate (2.6.5) is an accurate indicator
of
the true error. The size of
g'(
a)
also shows that the iterates
will
converge very slowly, and in this case,
xn+l
- xn
is
not an accurate indicator of
a-
xn.
Aitken's
extrapolation formula
is
simply (2.6.5), rewritten
as
an estimate of
a:
(2.6.7)
We denote this right side by
xn•'
for n
~
2.
By
substituting (2.6.3) into (2.6.7), the
formula for
x can be rewritten
as
n~2
(2.6.8)
which
is
the formula given in many texts.
Example
Use the results in Table 2.8 for iteration (2.6.6). With n = 7, using
either
(2.6.7) or (2.6.8),
x
7
= 6.0149518
a-
x
7
=
5.51E-
4
Thus the extrapolate x
7
is
significantly more accurate than x
7
•

86 ROOTFINDING FOR NONLINEAR EQUATIONS
We now combine linear iteration and Aitken extrapolation in a simpleminded
algorithm.
Algorithm Aitken (g, x
0
,
£,root)·
l.
Remark: It
is
assurried that lg'(a:)l < 1 and that ordinary linear
iteration using
x
0
will
converge·to
a:.
2.
3.
5.
Set
Xo
:=
x2
and
go
to step
2.
This algorithm will usually converge, provided the assumptions of step 1 are
satisfied.
Example
To
illustrate algorithm Aitken,
we
repeat the previous example (2.6.6).
The
numerical results are
given
in Table 2.9. The values x
3
,
x
6
,
and x
9
are the
Aitken extrapolates defined
by
(2.6.7). The values of
An
are given for only the
cases
n =
2,
5,
and
8,
since only then do the errors a -
xn,
a -
xn_
1
,
and
a-
xn-l
decrease linearly,
as
is
needed for
An~
g'(a).
Extrapolation
is
often used with slowly convergent linear iteration methods for
solving large systems of simultaneous linear equations. The actual methods used
are different from that previously described, but they also are based on the
general idea of finding the qualitative behavior of the error,
as
in (2.6.1), and of
then using that to produce an improved estimate of the answer. This idea
is
also
pursued in developing numerical methods for integration, solving differential
equations, and other mathematical problems.
Table
2.9
Algorithm Aitken applied to (2.6.6)
n
xn
An
a - xn
0 6.000000000000
1.55E-
2
1
6.000584501801
1.49E-
2
2
6.001145770761
.96025
1.44E-
2
3
6.014705147543
7.98E-
4
4
6.014733648720
7.69E-
4
5
6.014761128955
.96418
7.42E-
4
6
6.015500802060
2.27E-
6
7
6.015500882935
2.19E-
6
8
6.015500960931 .96439
2.11E-
6
9
6.015503072947
2.05E-
11
THE
NUMERICAL EVALUATION
OF
MULTIPLE ROOTS
87
2.
7 The Numerical Evaluation of Multiple Roots
We
say
that
the function
f(x)
has a
root
a of multiplicity p > 1
if
f(x)
=
(x-
aYh(x)
(2.7.1)
with
h(a)
* 0
and
h(x)
continuous
at
x
=a.
We
restrict p to be a positive
integer, although some
of
the following is equally valid for nonintegral values.
If
h(x)
is sufficiently differentiable
at
x =
a,
then (2.7.1) is equivalent to
/{a)
=/'{a)=···
=/(p-l)(a)
= 0
(2.7.2}
When finding a root
of
any function on a computer, there is always an interval
of
uncertainty
about
the root,
and
this is made worse when the root
is
multiple.
To
see this more clearly, consider evaluating
the
two functions /
1
(x)
= x
2
- 3
and
f
2
(x)
= 9 + x
2
(x
2
-
6).
Then
a =
f3
has multiplicity one as a root
of
/
1
and
multiplicity two as a root of /
2
•
Using four-digit decimal arithmetic,
/
1
(x)
< 0 for x
~
1.731, /
1
(1.732) = 0, and /
1
(x)
> 0 for x > 1.733. But /
2
(x)
= 0 for 1.726
~
x
~
1.738, thus limiting the
amount
of
accuracy that can be
attained
in
finding a root
of
/
2
(x).
A second example
of
the
etl"ect
of
noise in the
evaluation
of
a multipleorooLisillustrated for
f(x)
=
(x-
1)
3
in Figures 1.1 and
1.2
of
Section 1.3
of
Chapter
1.
For
a final example, consider the following
example.
Example Evaluate
f(x)
=
(x-
1.1)
3
{x-
2.1)
= x
4
-
5.4x
3
+ 10.56x
2
-
8.954x + 2.7951
(2.7.3)
on
an
IBM
PC
microcomputer using double precision arithmetic (in BASIC).
The
coefficients will not enter exactly because they
do
not have finite binary expan-
sions (except for the x
4
term).
The
polynomial
f(
x)
was evaluated in its
expanded form (2.7.3)
and
also using the nested multiplication scheme
f(x)
= 2.7951 +
x(
-8.954
+
x(10.56
+
x(
-5.4
+
x)))
Table 2.10 Evaluation of
.f(x)
=
(x-
1.1)
3
(x-
2.1)
x
f(x):
(2.7.3)
f(x):
(2.7.4)
1.099992
1.099994
1.099996
1.099998
1.100000
1.100002
1.100004
1.100006
1.100008
3.86E-
16
3.86E-
16
2.76E-
16
-5.55E-
17
5.55E-
17
5.55E-
17
-5.55E-
17
-1.67E-
16
-6.11E-
16
5.55E-
16
2.76E-
16
0.0
l.llE-
16
0.0
5.55E-
17
0.0
-1.67E-
16
-5.00E-
16
(2.7 .4)
88
ROOTFINDING
FOR NONLINEAR EQUATIONS
.Y
y = [(x!
Simple
root
Double
root
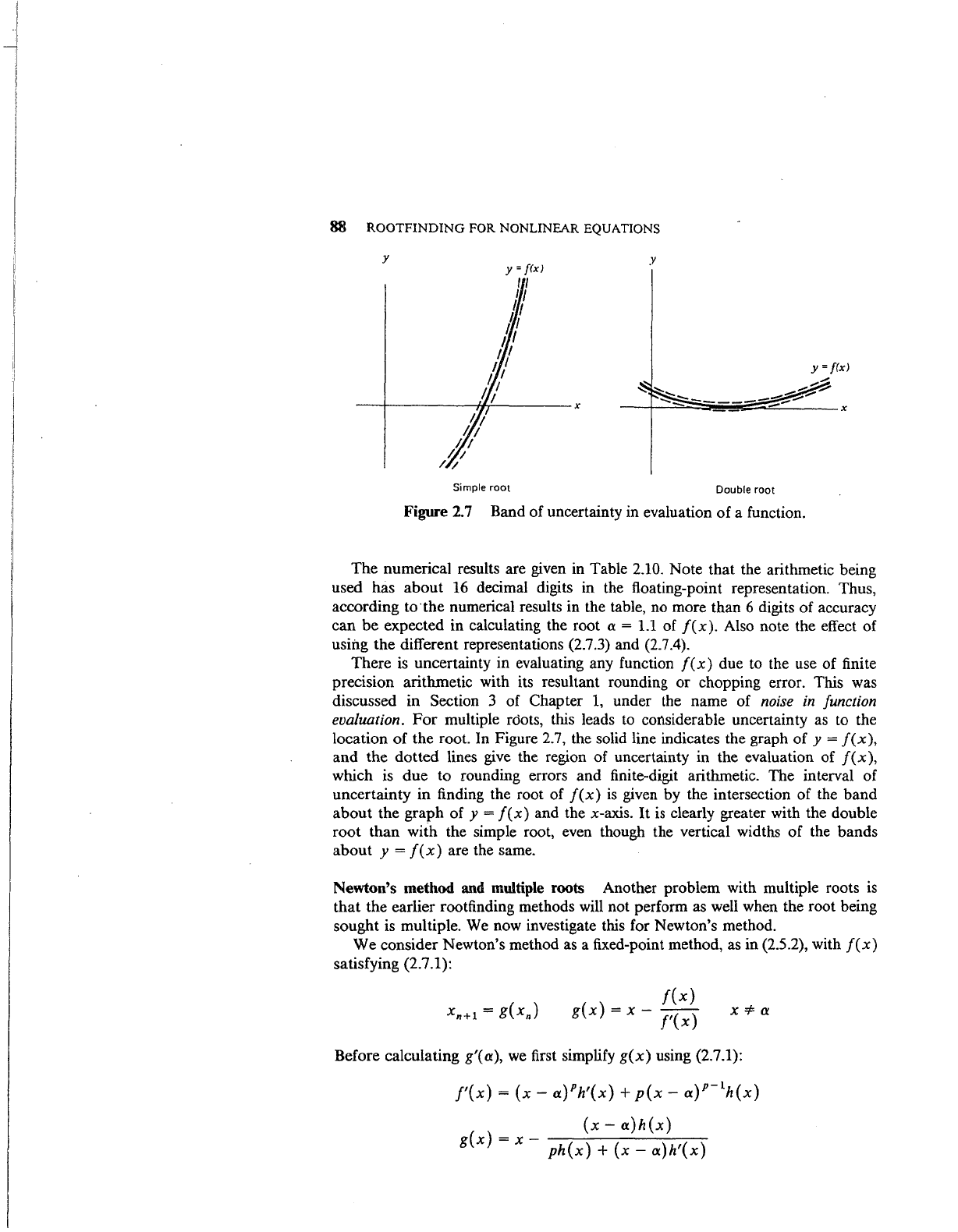
Figure 2.7 Band of uncertainty in evaluation
of
a function.
The
numerical results are given in Table 2.10. Note
that
the arithmetic being
used has
about
16 decimal digits in the floating-point representation. Thus,
according
to·the numerical results in the table, no more than 6 digits of accuracy
can
be
expected in calculating the root
a=
1.1
of
f(x).
Also note the effect of
using the different representations (2.7.3) and (2.7.4).
There
is
uncertainty in evaluating any function
f(x)
due to the use of finite
precision arithmetic with its resultant rounding or chopping error. This was
discussed in Section
3 of Chapter
1,
under the name of noise
in
function
evaluation.
For
multiple rdots, this leads to considerable uncertainty as to the
location
of
the root. In Figure 2.7, the solid line indicates the graph
of
y =
f(x),
and the dotted lines give the region of uncertainty in the evaluation of
f(x),
which is due to rounding errors and finite-digit arithmetic. The interval of
uncertainty in finding the root of
f(x)
is
given by the intersection of the
band
about
the graph
of
y =
f(x)
and the x-axis.
It
is
clearly greater with the double
root than
with the simple root, even though the vertical widths
of
the bands
about y
=
f(x)
are the same.
Newton's method and multiple roots Another problem with multiple roots
is
that
the earlier rootfinding methods will not perform as well when the root being
sought
is
multiple.
We
now investigate this for Newton's method.
We consider Newton's method as a fixed-point method, as in
(2.5.2), with
f(x)
satisfying (2.7.1):
f(x)
g(x)
=
x-
f'(x)
x=Fa
Before calculating
g'(a),
we
first simplify
g(x)
using (2.7.1):
f'(x)
=
(x-
a)Ph'(x) +
p(x-
a)P-
1
h(x)
(x-
a)h(x)
g(x) =
x-
ph(x)
+
(x-
a)h'(x)
I
J
THE
NUMERICAL EVALUATION
OF
MULTIPLE ROOTS
89
Table 2.11
Newton's method for (2.7.6)
n
x.
f(x.)
Ci
-
x.
0
1.22
-1.88E-
4
l.OOE-
2
1
1.2249867374
-4.71E-
5
5.01E-
3
2
1.2274900222
-1.18E-
5
2.51E-
3
3
1.2287441705
-2.95E-
6
1.26E-
3
4 1.2293718746
-7.38E-
7
6.28E-
4
5
1.2296858846
-1.85E-
7
3.14E-
4
18
1.2299999621
-2.89E-
15
3.80E-
8
19
1.2299999823
-6.66E-
16
1.77E-
8
20
1.2299999924
-l.llE-
16
7.58E-
9
21
1.2299999963
0.0
3.66E-
9
Differentiating,
and
h(x)
g'(x)
=
1
-
ph(x) +
(x-
a)h'(x)
d [
h(x)
l
-(x-
a)·-
dx
ph(x) +
(x-
a)h'(x)
1
g'(a)
= 1 - -
=I=
0
p
for p > 1
Ratio
.502
.501
.501
.500
.505
.525
.496
.383
(2.7.5)
Thus Newton's method
is
a linear method with rate
of
convergence
(p
-
1)/p.
Example Find the smallest root of
f(x)
=
-4.68999
+ x(9.1389 +
x(
-5.56
+
x))
(2.7 .6)
using Newton's method. The numerical results are shown in Table 2.11. The
calculations were done on an IBM PC microcomputer in double precision
arithmetic (in BASIC).
Only partial results are shown, to indicate the general
course
of
the calculation. The column labeled Ratio
is
the rate of linear
convergence
as
measured by
An
in (2.6.3).
The Newton method for solving for the root
of
(2.7.6)
is
clearly linear in this
case, with a linear rate of
g'(x)
=
t.
This
is
consistent with (2.7.5), since
a = 1.23 is a root of multiplicity p =
2.
The final iterates in the table are being
affected by the noise in the computer evaluation of
f(x).
Even though the
floating-point representation contains about
16
digits, only about 8 digits of
accuracy can
be
found in this case.

90 ROOTFINDING FOR NONLINEAR EQUATIONS
To
improve Newton's method,
we
would like a function
g(x)
for
which
g'(a)
=
0.
Based on the derivation of (2.7.5), define
Then easily,
g'(a)
=
0;
thus,
J(x)
g(x)
=
x-
p--
f'(x)
with
~~~
between xn and a. Thus
showing that the method
n = 0,
1,2,
...
,
(2.7.7)
has order of convergence
two,
the same
as
the original N
ewt<?n
method for simple
roots.
Example Apply (2.7.7) to the preceding example (2.7.6), using p = 2 for a
double root.
The
results are given in Table 2.12, using the same computer
as
previously.
The
iterates converge rapidly, and then they oscillate around the root.
The
accuracy (or lack of it) reflects the noise in
f(x)
and the multiplicity
of
the
root.
Newton's method can be used to determine the multiplicity
p,
as
in Table
2.11
combined with (2.7.5), and then (2,7.7) can be used
to
speed
up
the convergence
..
But the inherent uncertainty in the root due
to
th~
noise and the multiplicity will
remain. This can be removed only by analytically reformulating the rootfinding
problem as a new one
in
which the desired root a
is
simple. The easiest way to do
Table
2.12
Modified Newton's method (2.7.7), applied to (2.7.6)
n
x,
f(x,)
a-
X
11
0
1.22
-1.88E-
4
l.OOE-
2
1
1.2299734748
-1.31E-
9
2.65E-
5
2 1.2299999998
-l.llE-
16
1.85E-
10
3
1.2300003208
-1.92E-
13
-3.21E-
7
4
1.2300000001
-l.llE-
16
-8.54E-
11
5
1.2299993046
-9.04E-
13
6.95E-
7

BRENT'S ROOTFINDING ALGORITHM
91
this is
to
form the
(p-
l)st
derivative of
f(x),
and to then solve
(2.7 .8)
which
will
have
a.
as
a simple root.
Example The previous example had a root of multiplicity p =
2.
Then it
is
a
simple root
of
f'(x)
= 3x
2
-
11.12x + 9.1389
Using the last iterate in Table
2.11
as an initial guess, and applying Newton's
method to finding the root of
f'(x)
just given, only one iteration
was
needed to
find the value of
a.
to the full precision of the computer.
2.8 Brent's Rootfinding Algorithm
We describe an algorithm that combines the advantages of-the--bisection-method
and the secant method, while avoiding the disadvantages of each of them. The
algorithm
is
due to Brent (1973, chap. 4), and it
is
a further development of an
earlier algorithm due to Dekker
(1969). The algorithm results
in
a small interval
that contains the root.
If
the function
is
sufficiently smooth around the desired
root
f,
then the order of convergence
will
be superlinear,
as
with the secant
method.
In describing the algorithm
we
use the notation of Brent
(1973,
p.
47).
The
program
is
entered with two values, a
0
and b
0
,
for which
(1)
there
is
at least one
root
t of
f(x)
between a
0
and b
0
,
and
(2)
f(a
0
)f(b
0
)
~
0.
The program
is
also
entered with a desired tolerance
t, from which a stopping tolerance 8
is
produced:
0 = t + 2(1bl
(2.8.1)
with ( the unit round for the computer
[see
(1.2.11) of Chapter
1].
In a typical step of the algorithm, b
is
the best current estimate of the root t,
a
is
the previous value of
b,
and c
is
a past iterate that has been so chosen that
the root
f lies between b and c (initially c = a). Define m =
t(
c - b).
Stop the algorithm if
(1)
j(b)
=
0,
or
(2)
lml
~
o.
In either case, set the
approximate root
f =
b.
For case
(2),
because b will usually have been obtained
by the secant method, the root
f will generally be closer to b than to
c.
Thus
usually,
although all that can be guaranteed
is
that
If-
fl
s
2o

92
ROOTFINDING
FOR NONLINEAR EQUATIONS
If
the error test
is
not satisfied, set
b-a
i =
b-
/(b)
/(b)_
/(a)
(2.8.2)
Then set
b+c
if i lies between b and b + m =
--
2
otherwise [which
is
the bisection method]
In
the case that a,
b,
and· c are distinct, the secant method in the definition of i
is replaced by
an
inverse quadratic interpolation method. This results in a very
slightly faster convergence for the overall algorithm. Following the determination
of
b", define
{
b"
b'
= b + 8 · sign (
m)
if 1 b -
b"
1 > 8
if 1 b -
b"
1
~
8
(2.8.3)
If
you are some distance from the root, then b' = b". With ·this choice, the ·
method
is
(1) linear (or quadratic) interpolation, or
(2)
the bisection method;
usually it is (1) for a smooth function
f(x).
This generally results in a value of m
that does not become small. To obtain a small interval containing the root
t,
once
we
are close
to
it,
we
use
b'
:=
b + 8 · sign ( m ), a step of 8 in the direction
of
c.
Because
of
the
way
in which a new c
is
chosen, this
will
usually result in a
new small interval about
t.
Brent makes an additional important, but technical
step before choosing a new
b, usually the b' just given.
Having obtained the new
b',
we
set b = b',
a=
the old value of
b.
If
the sign
of
/(b),
using the
new
b,
is
the same
as
with the old
b,
the value of c
is
unchanged; otherwise, c
is
set to the old value of
b,
resulting in a smaller interval
about
t.
The accuracy of the value of b
is
now
tested,
as
described earlier.
Brent has taken great care to avoid underflow and overflow difficulties
with his
method,
but
the program is somewhat complicated to read
as
a consequence.
Example
Each of the following cases
was
computed on an IBM
PC
with 8087
arithmetic coprocessor and single precision arithmetic satisfying the IEEE stan-
dard
for floating-point arithmetic. The tolerance was t = 10-:
5
,
and thus
8 =
10-
5
+ 2ibl X (5.96 X
10-
8
)
='=
1.01
X
10-
5
since the root
of
t = 1 in all cases. The functions were evaluated in the form in
which they are given here, and in all cases, the initial interval was
[a,
b]
=
[0,
3].
The
table values for b and c are rounded to seven decimal digits.

BRENT'S ROOTFINDING ALGORITHM
93
Table 2.13 Example 1 of
Brent's method
b
/(b)
0.0
-2.00E
+ 0
0.5
-6.25E
-1
.7139038
-3.10E-
1
.9154507
-8.52E-
2
.9901779
-9.82E-
3
.9998567
-1.43E-
4
.9999999
-1.19E-
7
.9999999
-1.19E-
7
c
3.0
3.0
3.0
3.0
3.0
3.0
3.0
1.000010
Case (1)
f(x)
=
(x-
1)[1
+
(x-
1)
2
].
The numerical results are given in
Table
2.13. This illustrates the necessity
of
using b' = b + 8 · sign (
m)
in order
to
obtain a small interval enclosing the root
~-
Case (2)
f(x)
= x
2
-
1.
The numerical results are given in Table 2.14.
Case (3)
f(x)
=
-1
+ x(3 +
x(-
3 + x)).
The
root
is~=
1,
of multiplicity
three,
and
it took 50 iterations to converge to.
the
approximate root 1.000001.
With the initial values a =
0,
b =
3,
the bisection method would use only 19
iterations for the same accuracy.
If
Brent's method is compared with the
bisection method over the class of all continuous functions, then the number of
necessary iterates for an error tolerance of
8
is
approximately
(
b-
a)
log2
-8-
for bisection method
for Brent's algorithm
Table 2.14
Example
2of
Brent's method
b
/(b)
c
0.0
-1.00
3.0
.3333333
-8.89E-
1
3.0
.3333333
-8.89E
-1
1.666667
.7777778
-4.00E-
1
1.666667
1.068687 1.42E
-1
.7777778
.9917336
-1.65E-
2
1.068687
.9997244
-5.51E-
4
1.068687
1.000000
2.38E-
7
.9997244
1.000000
2.38E-
7
.9999900
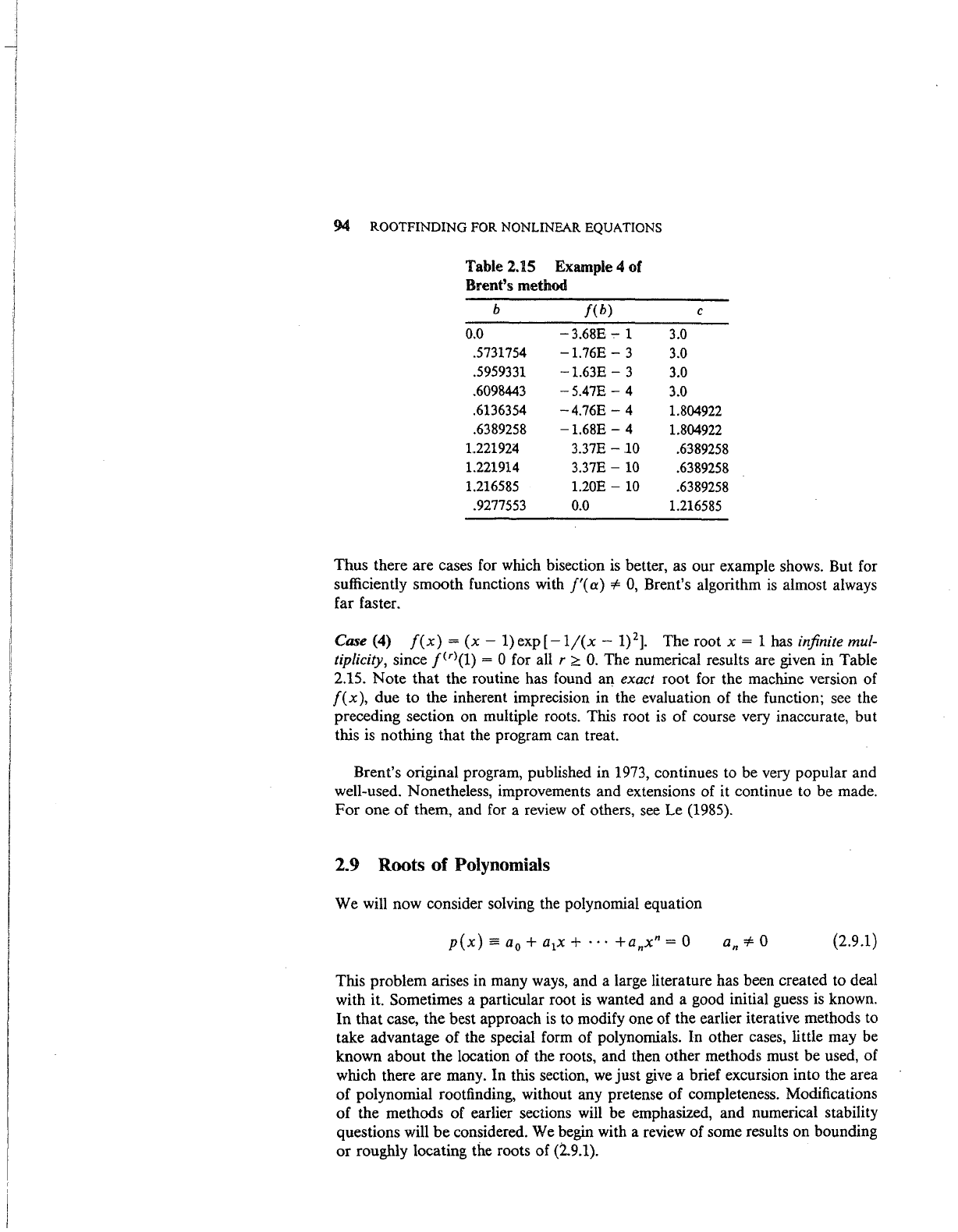
94 ROOTFINDING FOR NONLINEAR EQUATIONS
Table 2.15 Example 4 of
Brent's method
b
f(b)
c
0.0
-3.68E.,... 1
3.0
.5731754
-1.76E-
3
3.0
.5959331
-1.63E-
3
3.0
.6098443
-5.47E-
4
3.0
.6136354
-4.76E-
4
1.804922
.6389258
-1.68E-
4
1.804922
1.22192~
3.37E
-10
.6389258
1.221914
3.37E-
10
.6389258
1.216585
1.20E-
10
.6389258
.9277553
0.0
1.216585
Thus there are cases for which bisection
is
better,
as
our example shows. But for
sufficiently smooth functions with
f'(
a)
*
0,
Brent's algorithm
is
almost always
far faster.
Case (4)
f(x)
=
(x-
1) exp [
-1/(x-
1)
2
].
The root x = 1 has infinite mul-
tiplicity,
since
[<r>(1)
= 0 for all r
;;::
0.
The numerical results are given
in
Table
2.15. Note that the routine has found an exact root for the machine version of
f(x),
due to the inherent imprecision in the evaluation of the function;
see
the
preceding section on multiple roots. This root
is
of course very inaccurate, but
this
is
nothing that the program can treat.
Brent's original program, published in
1973, continues to be very popular and
well-used. Nonetheless, improvements and extensions of it continue
to
be made.
For
one of them, and for a
review
of others,
see
Le (1985).
2.9 Roots of Polynomials
We will now consider solving the polynomial equation
(2.9
.1)
This problem arises in many
ways,
and a large literature has been created to deal
with it. Sometimes a particular root
is
wanted and a good initial guess
is
known.
In
that case, the best approach
is
to
modify one of the earlier iterative methods to
take advantage of the special form of polynomials. In other cases, little may be
known about the location of the roots, and then other methods must be used, of
which there are many. In this section,
we
just
give
a brief excursion into the area
of polynomial rootfinding, without any pretense of completeness. Modifications
of the methods of earlier sections
will
be emphasized, and numerical stability
questions will
be
considered.
We
begin with a review of some results on bounding
or
roughly locating the roots of (2.9.1).
