Atkinson K. An Introduction to Numerical Analysis
Подождите немного. Документ загружается.


44 ERROR: ITS SOURCES, PROPAGATION, AND ANALYSIS
(b)
For
small values of
8,
measure the relative error in
sin(x)
==
x by
using
sin(x)-
x
sin(x)-
x
sin(x)
= x
x+O
Bound this modified relative error for lx I
.:s;:
8.
Choose 8 to make this
error less than
.01, corresponding to a 1 percent error.
4. Assuming g E
C[
a, b
],
show
5.
Construct a Taylor series for the following functions, and bound the error
when truncating after
n terms.
1
1
x
(a)
-
e-
12
dt
(b)
sin-
1
(x)
lxl < 1
X 0
1
xtan-
1
tdt
(c)
-;fo
t
(d)
cos(x)
+
sin(x)
(e)
log(l
-
x)
-1
<X<
1
(f)
[ 1
+X]
log--
.1-x
-1<x<1
6. (a) Using the result (1.1.11),
we
can show
1T
00
(
-1)2j+l
- =
tan-l
(1)
=
:E
---
4
j-0
2j
+ 1
and
we
can
obtain 1r
by-
multiplying
by
4. Why
is
this
not
a practical
way to compute
1r?
(b) Using a Taylor polynomial approximation, give a practical way to
evaluate
11.
7.
Using Taylor's theorem for functions of two variables, find linear
and
quadratic approximations to the following functions
f(x,
y)
for small
·values
of
x
and
y. Give the tangent plane function z =
p(x,
y)
whose
graph
is tangent to that of z =
f(x,
y)
at
(0, 0,
/(0,
0)).
(a)
..jl
+
2x
- y
(c) x ·
cos(x
..,..
y)
(b)
1+x
l+y
(d)
cos(x
+
V1r
2
+
y)

PROBLEMS
45
8. Consider the second-order divided difference
f[x
0
,
x
1
,
x
2
]
defined in
(1.1.13).
(a) Prove the property (1.1.15), that the order of the arguments
x
0
,
x
1
,
x
2
does not affect the value
of
the divided difference.
(b) Prove formula (1.1.14),
for some
r between the minimum
and
maximum
of
Xo,
X1, and
X2.
Hint: From part (a), there is no loss of generality in assuming
x
0
< x
1
< x
2
•
Use Taylor's theorem
to
reduce
f[x
0
,
x
1
,
x
2
],
expand-
ing about
x
1
;
and then use the intermediate value theorem to simplify
the error term.
(c) Assuming
f(x)
is
twice cOntinuously differentiable, show that
f[x
0
,
x
1
,
x
2
]
can be extended continuously to the case where some
or
all
of
the points x
0
,
x
1
,
and x
2
are-coincident.-For_example, show
exists and compute a formula for it.
9. (a) Show that the vector norms (1.1.16) and (1.1.18) satisfy the three
general properties of norms
that are listed following (1.1.18).
(b) Show
!lxlb
in (1.1.17)
is
a vector norm, restricting yourself to the
n
= 2 case.
(c) Show that the matrix norm (1.1.19) satisfies
(1.1.20) and (1.1.21).
For
simplicity, consider only matrices
of
order 2 X
2.
10. Convert the following numbers to their decimal equivalents.
(a) (10101.101h (b)
(2A3.FF)
16
(c) (.101010101
...
h
(d) (.AAAA
...
h
6
(e) (.00011001100110011
...
h
(f)
(11
...
1 h with the parentheses enclosing n 1s.
11.
To
convert a positive decimal integer x to its binary equivalent,

46 ERROR: ITS SOURCES, PROPAGATION, AND ANALYSIS
begin
by
writing
Based
on
this, use the following algorithm.
(i) x
0
==
x;
j
==
0
(H)
While x
1
=I=
0,
Do
the following:
a
1
==-Remainder
of
integer divide
x/2-
x
1
+
1
==Quotient
of
integer divide
x/2
j
:=j
+ 1
End
While
The
language
of
the algorithm should be self-explanatory. Apply it to
convert the following integers to their binary equivalents.
(a) 49 (b) 127 (c) 129
12.
To
convert a positive decimal fraction x < 1 to its binary equivalent
begin by writing
Based
on
this, use the following algorithm.
(i)
x
1
==
x;
j
==
1
(ii) While x
1
=I=
0,
Do
the following:
ai
==
Integer
part
of
2
·xi
xi+l
==
Fractional
part
of 2
·xi
j==j+1
End While
Apply this algorithm to convert the following decimal numbers to their
binary equivalents.
(a) .8125 (b) 12.0625 (c)
.1
(d)
.2
(e)
.4
(0
~
= .142857142857
...
13. Generalize Problems
11
and
12 to the conversion
of
a decimal integer to its
hexadecimal equivalent.

PROBLEMS 47
14.
Predict the output
of
the following section of Fortran code if it is run
on
a
binary computer
that
uses chopped arithmetic.
I=
0
X=
0.0
H =
.1
10
I=
I+
1
X=X+H
PRINT
*•
I,
X
IF
(X
.LT. 1.0) GO
TO
10
Would the outcome be any different if the statement
"X
=X
+
H"
was
replaced
by
"X
=
I*
H"?
15. Derive
the
bounds (1.2.9) for the relative error in the rounded floating-point
representation
of
(1.2.5)-(1.2.6).
16. Derive the upper
bound
result M =
pt
given in (1.2.16).
17. (a) Write a program to-create-an-overflow-error-on your computer.
For
example, input a number x and repeatedly square it.
(b)
Write
a program to experimentally determine the largest allowable
floating-point number.
18. (a) A simple model for population growth is
dN
-=kN
dt
with
N(t)
the population
at
time t and k >
0.
Show that this implies
a geometric rate
of
increase
L.1
population:
N(t+1)=CN(t)
t~t
0
Find
a formula for
C.
(b) A more sophisticated model for population growth is
dN
- =
kN[1-
bN]
dt
with
b,
k > 0 and 1 - bN
0
>
0.
Find the solution to this differential
equation problem. Compare its solution to that
of
part
(a). Describe
the differences in population growth predicted by the two models, for
both
large and small values
of
t.

..
!
j
48 ERROR: ITS SOURCES, PROPAGATION,
AND
ANALYSIS
19.
On
your
computer, evaluate the two functions
(a)
f(x)
= x
3
-
3x
2
+
3x
- 1
(b)
f(x)
= x
3
+
2x
2
-
x - 2
Evaluate them for a large sampling
of
values
of
x around
1,
and try to
produce the kind of behavior shown in Figure
1.2. Compare the results for
the two functions.
20. Write-a program to compute-experimentally
Limit(xP
+
yP)
11
P
p-oo
where x
and
y are positive numbers. First
do
the computation in the form
just
shown. Second, repeat the computation with the idea used in (1.3.8).
Run
the program for a variety of large
and
small values of X and
y,
for
example,
X=
y = 10
10
and
X=
y =
10-
10
•
21.
For
the following numbers x A and
Xr,
how many significant digits are
there
in
x A with respect to xr?
22.
23.
24.
25.
(a) X A = 451.023,
Xr
= 451.01
(b) X A = - .045113,
Xr
= - .045l8
(c)
XA
= 23.4213,
Xr
= 23.4604
Let all
of
the following numbers be correctly rounded to the number
of
digits shown: (a) 1.1062 + .947, (b) 23.46 - 12.753, (c) (2.747)(6.83), (d)
8.473/.064.
For
each calculation, determine the smallest interval in which
the result, using true instead
of
round,ed values, must be located.
Prove the formula
(1.4.5) for Rel(xAIYA).
Given the
~tion
x
2
-
40x + 1 =
0,
find its roots to
five
significant
digits.
Use
-./399
,;.
19.975, correctly rounded to
five
digits.
Give exact ways of avoiding loss-of-significance
errors
in
the following
computations.
(a)
log(x
+
1)-
log(x)
large x
(b)
sin(x)-
sin(y)
x = y
(c)
·tan(x)-
tan(y)
x = y

(d)
(e)
1-
cos(x)
x2
3
t1
+X
-
1,
PROBLEMS
49
x,;,o
x,;,o
26.
Use Taylor approximations to avoid the loss-of-significance error in the
following computations.
(a)
f(x)
=
_2_x_
(b)
log(1-
x)
+
xexl
2
f(x)
= 3
X
In
both cases, what is
Limit/(x)?
x-+0
27.
Consider evaluating
cos(x)
for large x
by
using the Taylor approximation
(1.1.5),
28.
29.
30.
x2
x2n
cos(x)
_:__1--
+
...
+(-1r--
2!
(2n)!
To
see the difficulty involved in using this approximation,
use
it
to
evaluate
cos (2
'IT)
=
1.
Determine n
so
that the Taylor approximation error
is
less
than
.0005. Then repeat the type of computation used
in
(1.4.17) and Table
1.2. How should cos (
x)
be evaluated for larger values of x?
Suppose you wish to compute the values of (a) cos (1.473), (b) tan -
1
(2.621),
(c)
ln
(1.471), (d) e
2
·
653
•
In
each case, assume you have only a table of values
of
the function with the argument x given
in
increments of
.01.
Choose the
table
value whose argument
is
nearest to your given argument. Estimate the
resulting error.
Assume that
x A = .937 has three significanJ digits with respect to
Xr.
Bound the relative error in xA ..
For
f(x)
=
1-
x,
bound the error and
relative error in
f(xA)
with respect to
f(xr).
The numbers given below are correctly rounded to the number of digits
shown. Estimate the errors in the function values in terms of the errors in
the arguments. Bound the relative errors.
(a) sin [(3.14)(2.685)] (b)
ln
(1.712)
(c) (1.
56
)3.414
31. Write a computer subroutine to form the sum

.50
ERROR: ITS SOURCES, PROPAGATION, AND ANALYSIS
in three ways: (1) from smallest to largest, (2) from largest to smallest, and
(3) in double precision, with a single precision rounding/chopping error at
the conclusion
of the summation. Use the double precision result to
find
the
error in the
two
single precision results. Print the results. Also write a main
program to create the following series in single precision, and use the
subroutine just given
to
sum the series. [Hint: In writing the subroutine, for
simplicity assume the terms of the series are arranged from largest to
smallest.]
(a)
n 1
2:--:-
(b>
1 1
n 1
L~
(c)
1 J
n 1
I:
-:J (d)
1 J
n (
-1)j
2:-.
J
32. Consider the product a
0
a
1
•••
am,
where a
0
,
a
1
,
•••
,
am
are m + 1 num-
bers stored in a computer that
uses
n digit base
fJ
arithmetic. Define
Pi=
fl(a
0
a
1
),
p
2
=
fl(a
2
p
1
),
p
3
=
fl(a
3
p
2
),
...
,
Pm
= fl(amPm-
1
).
If
we
write
Pm
= a
0
a
1
•••
am(! + w), determine an estimate for
w.
Assume that
a;
= fl
(a;),
i = 0,
1,
...
, m. What
is
a rigorous bound for
w?
What
is
a
statistical estimate
for
the
size
of
w?

TWO

ROOTFINDING
FOR NONLINEAR
EQUATIONS
Finding one
or
more roots of an equation
f(x)=O
(2.0.1)
is
one
of
the more commonly occurring problems of applied mathematics. In
most cases explicit solutions are not available and
we
must be satisfied with being
able to find a root to any specified degree of accuracy. The numerical methods
for finding the_roots-are-called
iterative methods,
and
they are the main subject of
this chapter.
We begin with iterative methods for solving (2.0.1) when
f(x)
is
any continu-
ously differentiable real valued function of a real variable x. The iterative
methods for this quite general class of equations will require knowledge of one
or
more initial guesses x
0
for the desired root
o:
of
f(x).
An initial guess x
0
can
usually
be
found by using the context in which the problem first arose; otherwise,
a simple graph of y =
f(x)
will often suffice for estimating x
0
•
A second major problem discussed in this chapter is that
of
finding one
or
more roots of a polynomial equation
(2.0.2)
The methods
of
the first problem are often specialized to deal with (2.0.2), and
that will be our approach. But there
is
a
large.
literature
on
methods that have
been developed especially for polynomial equations, using their special properties
in an essential way. These are the most important methods used in creating
automatic computer programs for solving (2.0.2),
and
we will reference some such
methods.
The third class of problems to be discussed
is
the solution
of
nonlinear systems
of
equations. These systems are very diverse in form, and the associated numeri-
cal analysis
is
both extensive and sophisticated.
We
will
just
touch on this
subject, indicating some successful methods that are fairly general in applicabil-
ity. An adequate development
of
the subject requires a good knowledge of both
theoretical and numerical linear algebra, and these topics are not taken up until
Chapters 7 through
9.
The last class of problems discussed in this chapter are optimization problems.
In this case,
we
seek to maximize or minimize a real valued function
/(x
1
,
.•.
,
xn)
and to find the point
(x
1
,
••.
,
xn)
at which the optimum is attained. Such
53
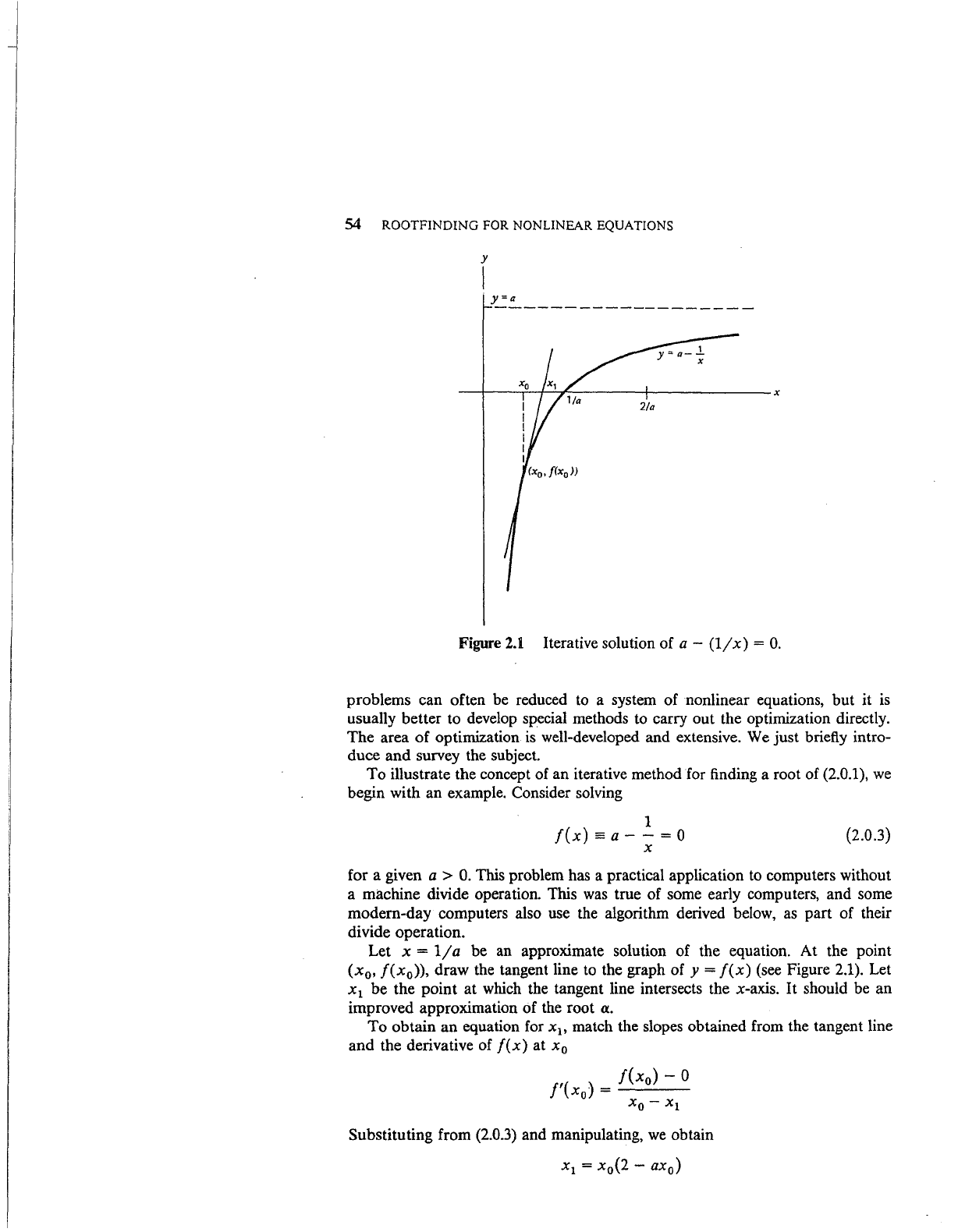
54
ROOTFINDING
FOR NONLINEAR EQUATIONS
y
I
y=a
Figure
2.1
Iterative solution of
a-
(1/x)
=
0.
problems can often be reduced
to
a system of nonlinear equations, but it
is
usually better to develop special methods to carry out the optimization directly.
The area
of
optimization
is
well-developed and extensive.
We
just briefly intro-
duce and survey the subject.
To illustrate the concept of an iterative method for finding a root of
(2.0.1),
we
begin with an example. Consider solving
1
/(x)=a--=0
X
(2.0.3)
for a given
a > 0. This problem has a practical application
to
computers without
a machine divide operation. This
was
true of some early computers, and some
modern-day computers also use the algorithm derived below,
as
part of their
divide operation.
Let
x =
1/a
be
an
approximate solution of the equation. At the point
(x
0
,
/(x
0
)),
draw the tangent line
to
the graph of y =
f(x)
(see Figure
2.1).
Let
x
1
be the point at which the tangent line intersects the x-axis. It should be an
improved approximation of the root
a.
To obtain an equation for x
1
,
match the slopes obtained from the tangent line
and the derivative of
f(x)
at x
0
/'(xo) =
/(x
0
) -
0
Xo-
xl
Substituting from
(2.0.3)
and manipulating,
we
obtain
x
1
= x
0
(2
-
ax
0
)
