Atkinson K. An Introduction to Numerical Analysis
Подождите немного. Документ загружается.


I
_.:/
CONVERGENCE AND STABILITY THEORY FOR MULTISTEP METHODS
401
for all 0 < h
~
h
0
•
Combined with (6.8.27) and (6.8.28),
Max
lenl
~
c3lt:lecz(b-xo)i>-i
x
0
s;·x.s;b
for an appropriate constant c
3
•
0 < h
~
h
0
•
Convergence
theory
The following result generalizes Theorem 6.6
of
Section
6.3, with necessary and sufficient conditions being given for the convergence of
multistep methods.
Theorem 6.8 Assume the consistency condition (6.8.7). Then the multistep
method (6.8.1) is convergent if and only if the root condition (6.8.9),
(6.8.10) is satisfied.
Proof
1.
We begin by showing the necessity
of
the root condition for conver-
gence, and again
we
use the problem
y'
=
0,
y(O) = 0, with the solution
Y(x)
=
0.
The multistep method (6.8.1) becomes
p
Yn+l
= L ajYn-j
j=O
with y
0
,
...
,
Yp
chosen to satisfy
1J(h)
= Max
IYnl
-+
0
Os;ns;p
n~p
(6.8.32)
as
h-+
0
(6.8.33)
Suppose that the root condition is violated. We show that (6.8.32) is not
convergent to
Y(
x)
=
0.
Assume that some l'j(O)I >
1.
Then a satisfactory solution
of
(6.8.32)
is
(6.8.34)
Condition (6.8.33) is satisfied since
But the solution {
Yn}
does
not
converge. First,
Consider those values
of
h =
bjN(h).
Then L'Hospital's rule can be
used to show that
b
Limit
-!r/O)
IN
=
00
N-+oo
N
showing (6.8.32) does
not
converge to the solution Y(x) =
0.

i
i
I
I
402 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS
Assume (6.8.9)
of
the root condition is satisfied,
but
that some 'j(O) is
a multiple
root
of
p(
r)
and
I 'j(O) I = 1.
Then
the preceding form
of
proof
is still satisfactory,
but
we must use
the
solution
0::;; n::;; N(h)
This completes the
proof
of
the necessity
of
the
root condition.
2. Assume that the
root
condition
is
satisfied. As with the previous
theorem, it is too difficult to give a general
proof
of
convergence for
an
arbitrary differential equation.
For
that, see
the
development in Isaacson
and
Keller (1966, pp.
405-417).
The
present
proof is restricted
to
the
model equation (6.8.13),
and
again we
assume
the
roots 'j(O) are distinct,
in
order
to
simplify the proof.
The
multistep method (6.8.1) becomes (6.8.18) for
the
model equation
y'
= 'Ay,
y(O)
=
1.
We show that
the
term
y
0
[r
0
(h'AW in its general
solution
p
Yn
=·
L "Yj['J(h'A)] n
{6.8.35)
j=O
will converge
to
the solution
Y(x)
=
e>..x
on
[0, b].
The
remaining terms
"Yj['j(h'A)r, j = 1, 2,
...
,
p,
are parasitic solutions,
and
they
can
be
shown
to
converge
to
zero as h
~
0 (see Problem 30).
Expand
r
0
(h'A) using Taylor's theorem,
From
(6.8.30),
o{1)
r~(O)
= p'(
1
)
and
using consistency condition (6.8.7), this leads to r
0
(0) =
1.
Then
over every finite interval 0
::;;
xn
::;;
b.
Thus
Max
jfro{h'A)]
n-
e>..x·l-
0
Osx.::;.b
as h
~
0
{6.8.37)
We
must
now show that the coefficient
'Yo-
1
ash
~
0.

CONVERGENCE AND STABILITY THEORY FOR MULTISTEP METHODS
403
The coefficients y
0
(
h),
...
,
Yp(
h)
satisfy the linear system
Yo
+
Yr
+ · · · +
Yp
=Yo
Yo[r
0
{hA)J
+ · · ·
+yph(hA)]
~
Y
1
Yofro(hA)]
P + · · · +yP[rP(hA)]
P,;,.
Yp
(6.8.38)
The initial values y
0
,
•••
,
Yp
depend on h and are assumed to satisfy
71(h)
=
Max
je'h•-
Ynl-
0
Osn:Sp
as
h-
0
But this implies
Limityn
= 1
h-+0
(6.8.39)
The coefficient y
0
can be obtained by using Cramer's rule to solve
(6.8.38):
Yo
1 1
Yr
rr
rP
Yp
rP
rP
1
p
Yo=
1 1 1
(6.8.40)
ro
rl
rP
r[
r{
rP
p
The denominator converges to the Vandermonde determinant for r
0
(0)
= 1, r
1
(0),
...
,
rp(O),
and this is nonzero since the roots are distinct.(see
Problem 1 of Chapter 3).
By
using (6.8.39), the numerator converges
to
the same quantity
as·
h - 0. ·Therefore, y
0
-
1 as h -
0.
Using this,
along with
(6.8.37) and Problem
30,
the solution {
Yn}
converges to
Y(x)
=
eh
on
[0,
b].
•
The following
is
a well-known result; it is a trivial consequence of Theorems
6.7 and
6.8.
Corollory Let (6.8.1) be a consistent multistep method. Then it
is
convergent if
and only if it is stable.
•
Relative stability and
weak
stability Consider again the model equation (6.8.13)
and its numerical solution
(6.8.22). The past theorem stated that the parasitic

404 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS
solutions
"Yj['j(hl\W
will converge
to
zero
as
h
-4
0.
But for a fixed h with
increasing xn, we also would like them to remain small relative to the principal
part
of
the
solution y
0
[r
0
(hA}r.
This will be true
if
the characteristic roots satisfy
j = 1, 2,
...
' p
(6.8.41)
for all sufficiently small values
of
h.
This leads us to the definition
of
relative
stability.
We say
that
the method (6.8.1) is relatively stable if the characteristic roots
'j(hl\)
satisfy (6.8.41) for all sufficiently small nonzero values
of
!hAl. And the
method is said to satisfy the strong root condition if
I'J(O)
I < 1
j =
1,2,
...
, p
(6.8.42)
This is an easy condition to check,
and
it implies relative stability. Just use the
co~tinuity
of
the roots
'j(hA)
with respect to
h;\
to have (6.8.42) imply (6.8.41).
Relative stability does not imply the strong root condition, although they are
equivalent for most methods [see Problem 36(b)].
If
a multistep method is stable
but
not
relatively stable, then
it
will
be
called weakly stable.
Example
1.
For
the midpoint method,
It
is weakly stable according to (6.8.41) when A <
0,
which agrees with what was
shown earlier
in
Section
6.4.
2.
The
Adams-Bashforth
and
Adams-Moulton
methods, (6.7.22)
and
(6.7.26),
have
the
same characteristic polynomial when h = 0,
p(r)
=
rp+I-
rP
(6.8.44)
The
roots
are
r
0
= 1,
rj
= 0, j = 1, 2,
...
,
p;
thus
the strong root condition is
satisfied
and
the
Adams methods are relatively stable.
Stability regions In the preceding 9iscussions
of
stability, the values
of
h were
required to
be
sufficiently small
in
order to carry through the derivations. Little
indication was given as to
just
how small h should be.
It
is clear that if h is
required to
be
extremely small, then the method is impractical for most prob-
lems; thus we need to examine the permissible values
of
h. Since the stability
depends
on
the
characteristic roots,
and
since they in turn depend
on
hA,
we are
interested
in
determining the values
of
hA
for which the multistep method (6.8.1)
is stable
in
some sense.
To
cover situations arising when solving systems
of
differential equations,
it
is
nec~ary
that the value
of
A
be
allowed to
be
complex, as
noted
following (6.8.17).
To
motivate the later discussion, we consider the stability
of
Euler's method.
Apply Euler's method to the equation
y'
=
Ay
+
g(x)
y(O) = Y
0
(6.8.45)

CONVERGENCE AND STABILITY THEORY FOR MULTISTEP METHODS 405
/
obtaining
n;::::;O
Yo=
Yo
(6.8.46)
Then consider the perturbed problem
n;::::
0 z
0
= Y
0
+
c::
(6.8.47)
For
the original Eq. (6.8.45), this perturbation of Y
0
leads to solutions
Y(x)
and
Z(x)
satisfying
Y(x)-
Z(x)
= c::eAx
x;::::
0
In this original problem,
we
would· ordinarily be interested in the case with
Real(;\).:::;;
0,
since then I
Y(x)-
Z(x)l
would remain bounded
as
x...,
0.
We
further restrict our interest to the case of Real ( ;\) <
0,
so that Y(
x)
- Z (
x)
...,
0
as x
...,
oo.
For such ;\,
we
want
to
find
the values of h so that the numerical
solutions
of
(6.8.46) and (6.8.47)
will
retain the behavior associated with
Y(x)
and
Z(x).
Let
e,.
=
z,.
-
y,..
Subtracting (6.8.46) from (6.8.47),
en+1
=
e,.
+ h;\e,. =
(1
+ h;\)e,.
Inductively,
en=
(1
+
h;\r£.
{6.8.48)
Then
e,....,
0 as
x,....,
oo
if and only if
11
+
h;\1
< 1
{6.8.49)
This yields a set of complex values
h;\
that form a circle of radius 1 about the
point
-1
in the complex plane.
If
h;\
belongs to this set, then
y,.
-
z,.
...,
0 as
xn...,
oo,
but
not otherwise.
To
see
that this discussion is also important for convergence, realize that the
original differential equation
can be looked upon
as
a perturbation of the
approximating equation
(6.8.46). From (6.2.17), applied to (6.8.45),
h2
Yn+l
=
Y,.
+ h[;\Yn + g{x..}] +
2Y"{~,.)
(6.8.50)
Here
we
have a perturbation of the equation (6.8.46)
at
every step, not at just the
initial point
x
0
=
0.
Nonetheless, the preceding stability analysis can be shown to
apply to this perturbation of
(6.8.46). The error formula (6.8.48)
will
have to be
suitably modified, but
it
will still depend critically on the bound (6.8.49) (see
Problem 40).
Example Apply Euler's method to the problem
y'
=
;\y
+
{1-
;\)cos(x)-
(1
+
;\)sin{x)
y(O)
= 1 (6.8.51)
406
NUMERICAL
METHODS FOR ORDINARY
DIFFERENTIAL
EQUATIONS
Table 6.17 Euler's method for (6.8.51)
"A
X Error: h =
.5
Error: h =
.1
Error: h =
.01
- 1
1
-2.46E-
1
-4.32E-
2
-4.22E-
3
2
-2.55E-
1
-4.64E-
2
-4.55E-
3
3
-2.66E-
2
-6.78E-
3
-7.22E-
4
4
2.27E-
1
3.91E-
2
3.78E-
3
5
2.72E-
1
4.91E-
2
4.81E-
3
-
10
1
3.98E-
1
-6.99E-
3
-6.99E-
4
2
6.90E + 0
-2.90E-
3
-3.08E-4
3
l.llE
+ 2
3.86E-
3
3.64E-
4
4 1.77E + 3
7.07E-
3
7.04E-
4
5 2.83E + 4
3.78E-
3
3.97E-
4
-50
1 3.26E + 0 1.06E + 3
-1.39E-
4
2 1.88E + 3
1.11E+9
-5.16E-
5
3
LOSE+ 6 1.17E +
15
8.25E-
5
4 6.24E + 8 1.23E +
21
1.41E-
4
5 3.59E +
11
1.28E +
27
7.00E-
5
whose true solution is
Y(x)
=
sin(x)
+
cos(x).
We give results for several
values
of
i\
and
h.
For
A=
-1,
-10, -50,
the
bound
(6.8.49) implies the
respective
bounds
on
h of
O<h<2
1
O<h<-=2
5 .
1
0 < h
<-
= .04
25
The use of larger values
of
h gives poor numerical results, as seen
in
Table 6.17.
The
preceding derivation with Euler's method motivates our general approach
to finding the set
of
all hA for which the method (6.8.1)
l.s
stable. Since we
consider only cases with Real (A) < 0, we want
the
numerical solution {
Yn}
of
(6.8.1), when applied to the model equation
y'
=
Ay,
to tend to zero as
xn
~
oo,
for all choices
of
initial values y
0
,
y
1
,
•••
,
Yr
The set
of
all hA for which this is
true is called
the
region
of
absolute stability
of
the method (6.8.1).
The
larger this
region, the less the restriction
on
h
in
order to have a stable numerical solution.
When (6.8.1) is applied to the
model
equation, we obtain the earlier equation
(6.8.18),
and
its solution is given by (6.8.22), namely
p
Yn
= L
rArihA)]
n
n;;o:O
j=O
provided
the
characteristic roots r
0
(hA),
...
, r
0
(hi\)
are distinct.
To
have this
tend to zero as n
~
oo, for all choices
of
y
0
,
...
,
yP,
it
is necessary
and
sufficient
to have
h(hA)
I < 1
j =
0,1,
...
, p (6.8.52)
CONVERGENCE AND STABILITY THEORY
FOR
MULTISTEP METHODS
407
The set of all
hA.
satisfying this set of inequalities
is
also called the region of
absolute stability. This region
is
contained in the set defined in the preceding
paragraph, and
it
is
usually equal to that set.
We
work only with (6.8.52) in
finding the region of absolute stability.
Example Consider the second-order Adams-Bashforth method
h
Yn+l
= Yn +
2[3y~-
Y~-1]
n~1
The characteristic equation
is
and its roots are
Imaginary
3.00
_
_,k,_=_,1,__+-~-"--f~'4-~C&--------...__
Real
-2.00
-3.00
k=6
k=5
k=4
2.00
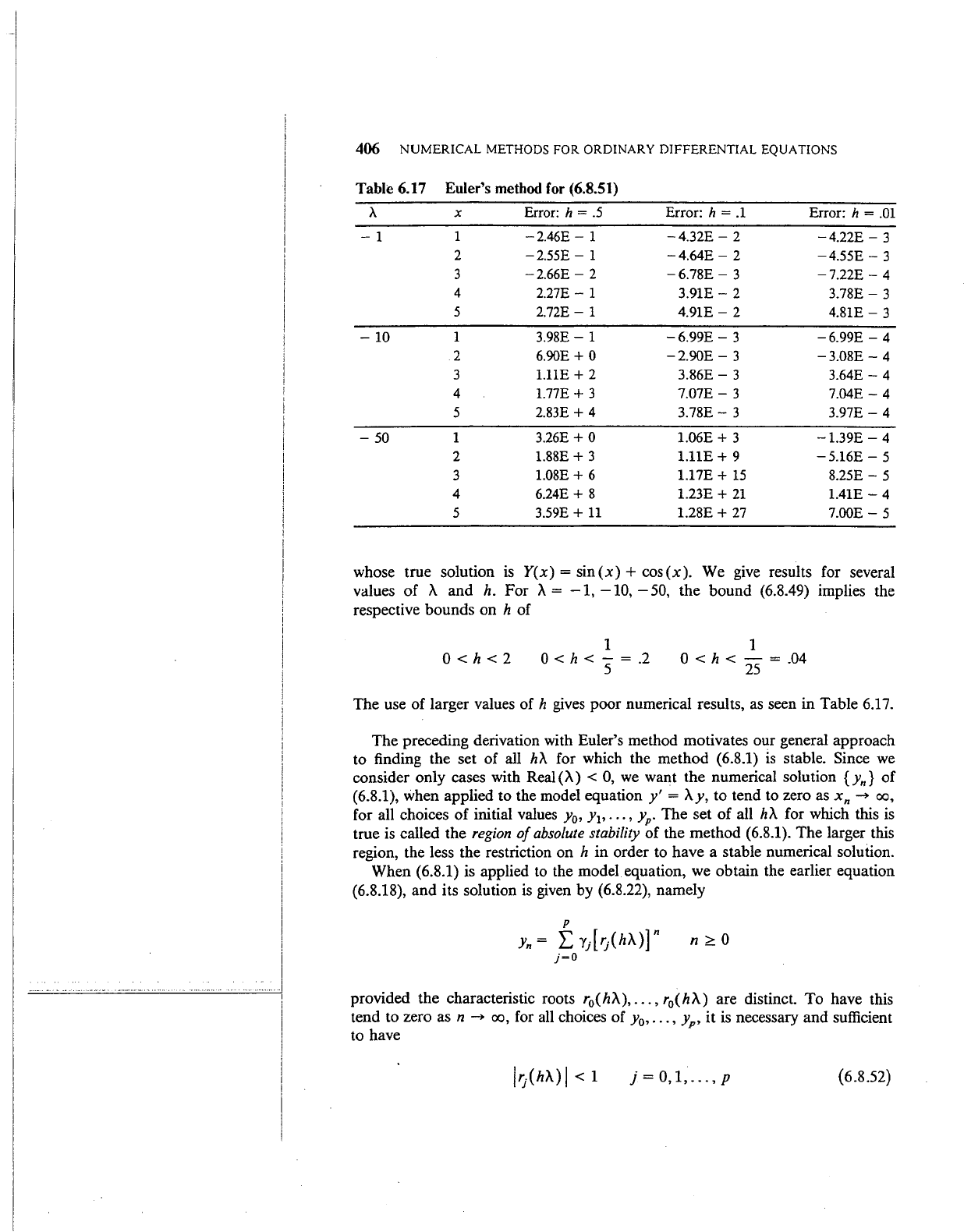
Figure
6.7 Stability regions for Adams-Bashforth
methods. The method of order
k
is
stable inside the
region indicated left of origin. [Taken from Gear (1971),
p.
131,
with permission.]
(6.8.53)
408
NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS
Imaginary
Real
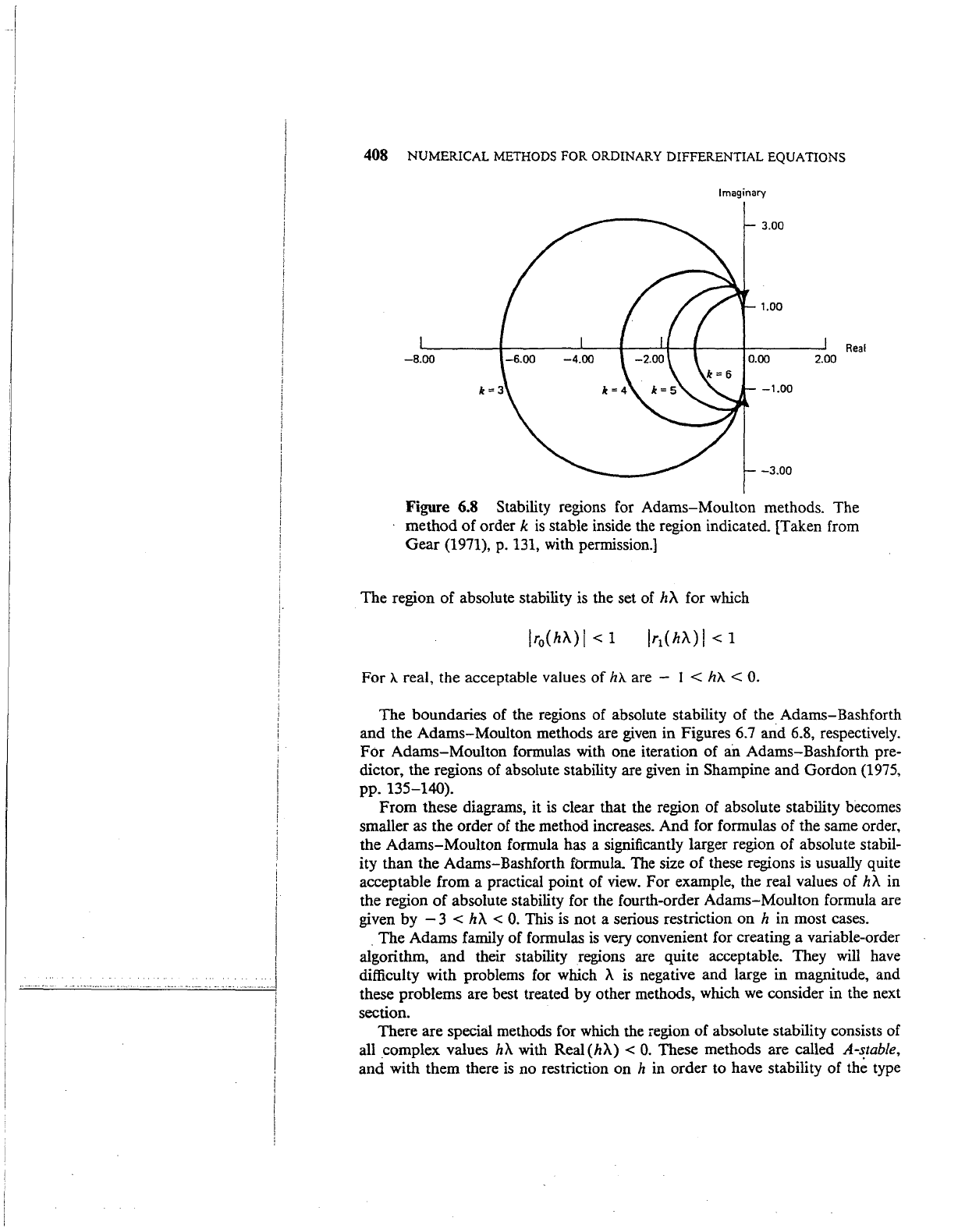
Figure 6.8 Stability regions for Adams-Moulton methods. The
method
of
order k
is
stable inside the region indicated. [Taken from
Gear
(1971), p. 131, with permission.]
The region of absolute stability is the set of
hA.
for which
h(hA.)
I < 1
For
X.
real, the acceptable values
of
hX.
are - I <
hX.
< 0.
The boundaries of the regions of absolute stability of theAdams-Bashforth
and the Adams-Moulton methods are given in Figures
6.7 and 6.8, respectively.
For
Adams-Moulton formulas with one iteration of an Adams-Bashforth pre-
dictor, the regions of absolute stability are given in Shampine and Gordon (1975,
pp.
135-140).
From these diagrams, it
is
clear that the region of absolute stability becomes
smaller
as
the order of the method increases. And for formulas of the same order,
the Adams-Moulton formula has a significantly larger region of absolute stabil-
ity than the Adams-Bashforth formula. The size
of
these regions
is
usually quite
acceptable from a practical point of
view.
For example, the real values of
hA.
in
the region
of
absolute stability for the fourth-order Adams-Moulton formula are
given by - 3
<
hA.
<
0.
This is not a serious restriction on h in most cases .
. The Adams family of formulas
is
very convenient for creating a variable-order
algorithm, and their stability regions are quite acceptable. They
will
have
difficulty with problems for which
A.
is
negative and large in magnitude, and
these problems are best treated by other methods, which
we
consider in the next
section.
There are special methods for which the region of absolute stability consists of
all
.complex values hX with Real(hX) <
0.
These methods are called
A-~tab/e,
and with them there
is
no restriction on h in order to have stability of the type

CONVERGENCE AND STABILITY THEORY FOR MULTISTEP METHODS
409
Table 6.18
Example of trapezoidal rule: h =
.5
X
Error:
A=
-1
Error: A =
-10
Error: A =
-50
2
-1.13£-
2
-2.78£-3
-7.91£-4
4
-1.43£-
2
-8.91£-
5
-8.91£-
5
6
2.02E-
2
2.77£-
3
4.72£-4
8
-2.86£-3
-2.22£-3
-5.11£-
4
10
-1.79£-
2
-9.23£-4
-1.56£-4
we
have been considering. The trapezoidal rule
is
an example of such a method
[see
(6.5.24)-(6.5.25)].
Example Consider the backward Euler method:
Yn+l
=
Yn
+
hf(xn+l•
Yn+l)
n~O
Applying this to the model equation
y'
=
Ay
and solving,
we
have
Then
Yn-
0
as
xn-
oo
if and only if
1
<1
11-
hAl
n~O
(6.8.54)
( 6.8.55)
This will be true for all
hA
with Real(A) <
0,
and the backward Euler method
is
an A-stable method.
Example Apply the trapezoidal method to the problem (6.8.51), which was
solved earlier with Euler's method.
We
use a stepsize
of
h =
.5
for
A=
-1,
-10,
-50.
The results are given in Table
6.18.
They illustrate that the
trapezoidal rule does not become unstable
as
1 A 1 increases, while Real (A) <
0.
It
would be useful to have A-stable multistep methods of order greater than
2.
But a result of Dahlquist (1963) shows there are no such methods. We examine
some higher order methods that have most
of
the needed stability properties in
the following section.
6.9 Stiff Differential Equations and the Method of Lines
The numerical solution of stiff differential equations has, within the past ten to
fifteen years, become a much studied subject. Such equations (including systems
of differential equations) have appeared in an increasing number
of
applications,
in subjects as diverse
as
chemical kinetics and the numerical solution
of
partial
differential equations. In this section,
we
sketch some
of
the main ideas about this

'
i
I
·•
~
m
···•••···••••••·••~
410 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS
subject, and we show its relation to the numerical solution
of
the simple heat
equation.
There are many definitions
of
the concept
of
stiff differential equation. The
most important common feature of these definitions is that when such equations
are being solved with standard numerical methods (e.g., the Adams
methods
of
Section 6.7), the stepsize h
is
forced to be extremely small in order to maintain
stability-far
smaller than would appear to
be
necessary based on a considera-
tion
of
the truncation error. An indication
of
this can be seen with Eq. (6.8.51),
which was solved in Table 6.17 with Euler's method.
In
that case, the unknown
Y(x)
did
not
change with
A,
and therefore the truncation error was also
independent
of
A.
But the actual error
was
strongly affected by the magnitude
of
A,
with
hA
required to satisfy the stability condition
11
+hAl
< 1 to obtain
convergence. As
IAI
increased, the size of h
had
to
decrease accordingly. This is
typical of
the
behavior of standard numerical methods when applied to stiff
differential equations, with the major difference being that the actual values of
IAI
are far larger
in
real life examples, for example, A =
-10
6
•
We now look at the most
comq1.0n
class
of
such differential equations, basing
our
examination
on
consideration
of
the linearization of the system y' =
f(x,
y)
as developed
in
(6.8.14)-(6.8.17):
y'
= Ay +
g(x)
(6.9.1)
with A =
fy(x
0
,
Y
0
)
the Jacobian matrix of f. We say the differential equation
y'
=
f(x,
y) is
stiff
if some of eigenvalues Aj of A, or more generally of
fy(x,
y),
have a negative real part of very large magnitude. We study numerical methods
for stiff equations
by
considering their effect
on
the model equation
y'=Ay+g(x)
{6.9.2)
with Real
(A)
negative and very large in magnitude. This approach has its
limitations, some
of
which
we
indicate later,
but
it
does give us a means
of
rejecting unsatisfactory methods, and
it
suggests some possibly satisfactory
methods.
The
concept
of
a region of absolute stability, introduced in the last section, is
the initial tool used in studying the stability
of
a numerical method for solving
stiff differential equations. We seek methods whose stability region contains the
entire negative real axis and as much of the left half of the complex plane as
possible.
There
are a number of ways to develop such methods,
but
we
only
discuss one
of
them-obtaining
the backward differentiation formulas (BDFs).
Let
PP(x) denote the polynomial
of
degree
~
p that interpolates Y(x)
at
the
points
Xn+l•
Xn,
•.•
,
Xn-p+l
for some
p;;:::
1:
p-1
PP{x) = L
Y(xn-j)lj,n(x)
j=
-1
(6.9.3)
with {lj,
n(
x)}
the Lagrange interpolation basis functions for the nodes
