Atkinson K. An Introduction to Numerical Analysis

THE TRAPEZOIDAL METHOD

371

with z

0

= Y

0

+ t:. To analyze the effect of the perturbation in the initial value, let

wn

=

zn-

Yn·

Subtracting,

n~O

( 6.5.23)

This is simply the trapezoidal method applied

to

our model problem, except that

the initial value

is

t:

rather than

1.

The numerical solution in (6.5.23) is simply

t:

times that obtained in the numerical solution· of (6.5.20). Thus the behavior of the

numerical solution of the model problem (6.5.20) will

give

us the stability

behavior of the trapezoidal rule applied

to

(6.5.21).

The model problems in which

we

are interested are those for which A

is

real

and

negative

or

A is complex with negative real part. The reason for this choice is

that then the differential equation problem (6.5.21) is well-conditioned,

as

noted

in (6.1.8), and the major interesting cases excluded are

A = 0 and A strictly

imaginary.

Applying the trapezoidal rule to (6.5.20),

Then

Inductively

hA

Yn+I

=

Yn

+

T(Yn

+

Yn+I]

[

1

+

(hA/2)]

Yn+I

=

1

_

(hA/

2

)

Yn

=

[1

+

{hA/2)]n

Yn

1-

{hA/2)

Yo=

1

n~O

provided

hA

=F

2.

For the case of real A <

0,

write

1

+

(hA/2)

hA

2

r=

=1+

=-1+----

1 -

(hA/2)

1 -

(hA/2)

. 1 -

(hA/2)

This shows - 1 < r < 1 for

all

values of h >

0.

Thus

. Limityn

= 0

n->oo

(6.5.24)

(6.5.25)

There are

no

limitations on h

in

order to have boundedness. of

{Yn},

and thus

stability of the numerical method in (6.5.22)

is

assured for all h > 0 and all

======================'· J A <

0.

This is a stronger statement than is possible with most numerical methods,

where generally

h must be sufficiently small to ensure stability.

For

certain

applications, stiff differential equations, this is an important consideration. The

property that (6.5.25) holds for

all h > 0 and all complex A with Real(A) < 0 is

called

A-stability.

We

explore it further

in

Section 6.8 and Problem

37.

372

NUMERICAL

METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS

Richardson error estimation This error estimation

was

introduced in Section

5.4,

and

it was used both to predict the error [as in (5.4.42)] and to obtain a more

rapidly convergent numerical integration method

[as

in (5.4.40)].

It

can also be

used in both

of

these ways in solving differential equations, although we will use

it mainly to predict the error.

Let

Yh(x)

and y

2

h(x)

denote the numerical solutions to

y'

=

j(x,

y)

on

[x

0

,

b], obtained using the trapezoidal method (6.5.2). Then using (6.5.19),

Y(xJ-

Yh(xn)

=

D(xn)h

2

+

O(h

3

)

Y(xn)-

Y2h(xn) =

4D(xn)h

2

+

O(h

3

)

Multiply the first equation by four, subtract the second, and solve for

Y(xn):

(6.5.26)

The formula

on

the right side has a higher order of convergence than the

trapezoidal method, but note that it requires the computation of

yh(xn)

and

y

2

h(xn) for all nodes xn in [x

0

,

b].

The formula (6.5.26)

is

of greater use in predicting the global error in

yh(x).

Using (6.5.26),

The left side is

O(h

2

),

from (6.5.19), and thus the first term on the right side must

also be

0(

h

2

).

Thus

(6.5.27)

is

an

asymptotic estimate of the error. This

is

a practical procedure for estimating

the global error, although the way we have derived it does not allow for a variable

stepsize in the nodes

..

Example Consider the problem

y'

=

-y2

y(O) = 1

Table 6.8

Trapezoidal

~ethod

and Richardson error estimation

X

Y2h(x)

Y(x)-

y

21

,(x)

Yh(x)

Y(x)-

Yh(x)

f[yh(x)

- Y2h(x)]

1.0

.483144 .016856 .496021

.003979 .004292

2.0

.323610 .009723 .330991

.002342

.002460

3.0

.243890 .006110

.248521 .001479 .001543

4.0

.194838

.004162

.198991 .001009 .001051

5.0

.163658

.003008

.165937

.000730 .000759

A LOW-ORDER PREDICTOR-CORRECTOR ALGORITHM

373

which has the solution

Y(x)

=

1/(1

+

x).

The results in Table

6.8

are for

stepsizes

h =

.25

and 2h =

.5.

The last column

is

the error estimate (6.5.27), and

it is an accurate estimator of the true error

Y(x)-

yh(x).

6.6 A Low-Order Predictor-Corrector Algorithm

In this section, a fairly simple algorithm is described for solving the initial value

problem

(6.0.1).

It

uses

the trapezoidal method (6.5.2), and it controls the size of

the local error by varying the stepsize

h. The method is not practical because of

its low order of convergence, but it demonstrates some of the ideas and

techniques involved

in

constructing a variable-stepsize predictor-corrector al-

gorithm.

It

is

also simpler to understand than algorithms based on higher order

methods.

Each step from xn

to

xn+

1

will consist of constructing

Yn+

1

from

Yn

and

Yn-

1

,

and

Yn+

1

will be an approximate solution of (6.5.2) based on using some iterate

from

(6.5.3). A regular step has xn+

1

-

xn

=

xn-

xn_

1

=

h,

the midpoint

predictor (6.5.15)

is

used, and the local error is predicted using the difference of

the predictor and corrector formulas. When the stepsize is being changed, the

Euler predictor (6.5.12)

is

used.

The user of the algorithm

will

have to specify several parameters in addition to

those defining the differential equation problem (6.0.1). The stepsize

h will vary,

and the user must specify values

h min and h max that limit the size of h. The user

should also specify an initial value for

h; and the value should be one for which

ihfy(x

0

,

y

0

)

is

sufficiently less than 1 in magnitude, say less than 0.1. This

quantity

will

determine the speed of convergence of the iteration in (6.5.3) and

is

discussed later in the section, following the numerical example. An error toler-

ance

t:

must be given, and the stepsize h

is

so chosen that the local error trunc

satisfies

(6.6.1)

at

each step. This

is

called controlling the error

per

unit stepsize. Its significance is

discussed near the end of the section.

The notation of the preceding section

is

continued. The function

un(x)

is the

solution of

y'

=

f(x,

y)

that passes through

(xn,

Yn). The local error to be

estimated and controlled

is

(6.5.11), which

is

the error in obtaining un(xn+

1

)

using the trapezoidal method:

h =

Xn+

1

-

Xn

(6.6.2)

If

Yn

is sufficiently close to Y(xn), then this is a good approximation to the

closely related truncation error in (6.5.1):

i

------·----·-·------·-----·---------··------·····--·")

I

~j

374

NUMERICAL

METHODS FOR

ORDINARY

DIFFERENTIAL

EQUATIONS

And

(6.6.2)

is

the only quantity for which

we

have the information needed to

control it.

Choosing the initial stepsize The problem

is

to

find

an initial value of h and

node x

1

= x

0

+

h,

for which

IY

1

-

Y(x

1

)1

satisfies the bounds in (6.6.1). With

the initial

h supplied by the user, the value Jh(x

1

)

is obtained by using the Euler

predictor

(6.5.12) and iterating twice in (6.5.3). Using the same procedure, the

values

yh

12

(x

0

+

h/2)

and Yh;

2

(x

1

)

are also calculated. The Richardson ex-

trapolation procedure

is

used to predict the error in Yh(x

1

),

(6.6.3)

If

this error satisfies the bounds of (6.6.1), then the value of h

is

accepted, and

the regular trapezoidal step using the midpoint predictor

(6.5.15)

is

begun. But if

(6.6.1) is

not

satisfied by (6.6.3), then a new value of h

is

chosen.

Using the values

obtain the approximation

(6.6.4)

This is

an

approximation using the second-order divided difference of Y' =

f(x,

Y); for example, apply Lemma 2 of Section 3.4. For any small stepsize h,

the truncation error at x

0

+ h is well approximated by

The new stepsize

h is chosen so that

_r£

h = v

TD;YI

(6.6.5)

This should place the initial truncation error in approximately the middle of the

range (6.6.1) for the error per unit step criterion. With this new value of

h, the

test using (6.6.3) is again repeated,

as

a safety check.

By

choosing h so that the truncation error will satisfy the bound (6.6.1) when

it is doubled

or

halved,

we

ensure that the stepsize will not have to be changed

A LOW-ORDER PREDICTOR-CORRECTOR ALGORITHM

375

for several steps, provided the derivative Y(3)(x) is not changing rapidly. Chang-

ing the stepsize

will

be more expensive than a normal step, and

we

want to

minimize the need for such changes.

The regular predictor-corrector step The stepsize

h satisfies

xn-

xn-l

=

xn+l-

xn

=h.

To

solve

for the value

Yn+l•

use the midpoint predictor (6.5.15)

and iterate once in (6.5.3). The local error (6.5.11)

is

estimated using (6.5.17):

1 h

3

-

-("

-

y<

0

> ) = -

-u<

3

>(x

) +

O(h

4

)

6

Jn+l

n+l

12 n n

(6.6.6)

Thus

we

measure the local error using

(6.6.7)

If

trunc satisfies (6.6.1), then the value of h is not changed and calculation

continues with this regular step procedure. But when (6.6.1) is not satisfied, the

values

Yn+l

and

xn+l

are discarded, and a new stepsize is chosen based on the

value

of

trunc.

Changing the stepsize

Using (6.6.6), -

trunc

h~

where h

0

denotes the stepsize used in obtaining trunc.

For

an arbitrary stepsize

h, the local error in obtaining

Yn+l

is estimated using

Choose

h so that

[

h

]3

1

ho

jtruncj = 2£h,

(6.6.8)

Calculate

Yn+l

by using the Euler predictor and iterating twice

in

(6.5.3). Then

return

to

the regular predictor-corrector

st~p.

To

avoid rapid changes in h that

can lead to significant errors, the new value of

h is never allowed

to

be more than

twice the previous value.

If

the new value of h is less than h min• then calculation

'

I

----------------------------------------··--·---··--

j

376 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS

·is

terminated. But if the

new

value of h

is

greater than h

max•

we

just

let h = h max

and proceed with the calculation. This has possible problems, which are discussed

following the numerical example.

Algorithm Detrap(J, x

0

,

y

0

,

X

end•

£,

h, h min•

hmax•

ier)

1.

Remark: The problem being solved

is

Y' =

f(x,

Y), Y(x

0

)

=

y

0

,

for x

0

:S:

x

:S:

Xend•

using the method described earlier in the

section. The approximate solution values are printed at each

node point. The error parameter

f and the stepsize parameters

were discussed earlier in the section. The variable ier

is

an

error indicator, output when exiting the algorithm: ier =

0

means a normal return; ier = 1 means that h = h max

at

some

node points; and ier = 2 means that the integration was

terminated due to a necessary.

h < h min·

2. Initialize: loop

==

1, ier

==

0.

3. Remark: Choose an initial value of

h.

4. Calculate Yh(x

0

+h),

Yh;

2

(x

0

+

(h/2)),

Yh;

2

(x

0

+h)

using

method (6.5.2). In each case, use the Euler predictor (6.5.12)

and follow it by two iterations of

(6.5.3).

5. For the error in Yh(x

0

+h),

use

6.

If

±Eh

:s;

!trunci

:s;

Eh,

or if loop =

2,

then x

1

==

x

0

+ h,

y

1

==

Yh(x

0

+ h), print x

1

,

y

1

,

and go to step 10.

7.

Calculate D

3

y

,;,

y<3>(x

0

)

from (6.6.4).

If

D

3

y *

0,

then

If

D

3

y =

0,

then h

==

h max and loop

==

2.

8.

If

h <

hmin•

then ier := 2 and exit.

If

h >

hmax•

then h

==

hmax•

ier

==

1,

loop==

2.

9.

Go to step

4.

10. Remark: This portion of the algorithm contains the regular

predictor-corrector step with error control.

A LOW-ORDER PREDICTOR-CORRECTOR ALGORITHM

377

1L

Let x

2

•=

x

1

+

h,

and

y4°)

•=

Yo+

2hf(x

1

,

y

1

).

Iterate (6.5.3)

once to obtain

y

2

•

13.

If

jtruncj >

£h

or

jtruncj <

i£h,

then go to step 16.

14.

Print x

2

,

h

15.

x

0

==

x

1

,

x

1

•=

x

2

,

y

0

==

y

1

,

y

1

•=

Y2·

If

x

1

< xend• then go to

step 11. Otherwise exit.

16. Remark: Change the stepsize.

17.

x

0

:=

x

1

,

y

0

•=

y

1

,

h

0

==

h,

and

calculate h using (6.6.8)

18.

h

:=

Min {

h,

2h

0

}.

19.

If

h < hmm, then ier

•=

2

and

exit.

If

h >

hmax•

then ier

:=

1

and

h

·=

h max·

20.

yf

0

>

•=

Yo

+

hf(x

0

,

y

0

),

and

iterate twice

in

(6.5.3) to calculate

y

1

•

Also, x

1

:=

x

0

+h.

21. Print x

1

,

Jt.

22.

If

x

1

<

xend,

then go to step 10. Otherwise, exit.

The

following example uses

an

implementation

of

Detrap that also prints trunc.

A section

of

code was added to predict the truncation error in y

1

of

step 20.

Example Consider the problem

which has the solution

1

y'

=

----

2y2

1 + x

2

X

Y(x)

= 1 +

x2

y(O)

= 0 (6.6.9)

This is

an

interesting problem for testing Detrap,

and

it performs quite well.

The

equation was solved

on

[0,

10]

with

hmin

= .001,

hmax

= 1.0, h = .1,

and

£ =

.0005. Table 6.9 contains some

of

the results, including the true global

error

and

the true local error, labeled True le. The latter was obtained

by

using

another

more accurate numerical method. Only selected sections

of

output

are shown

because

of

space.

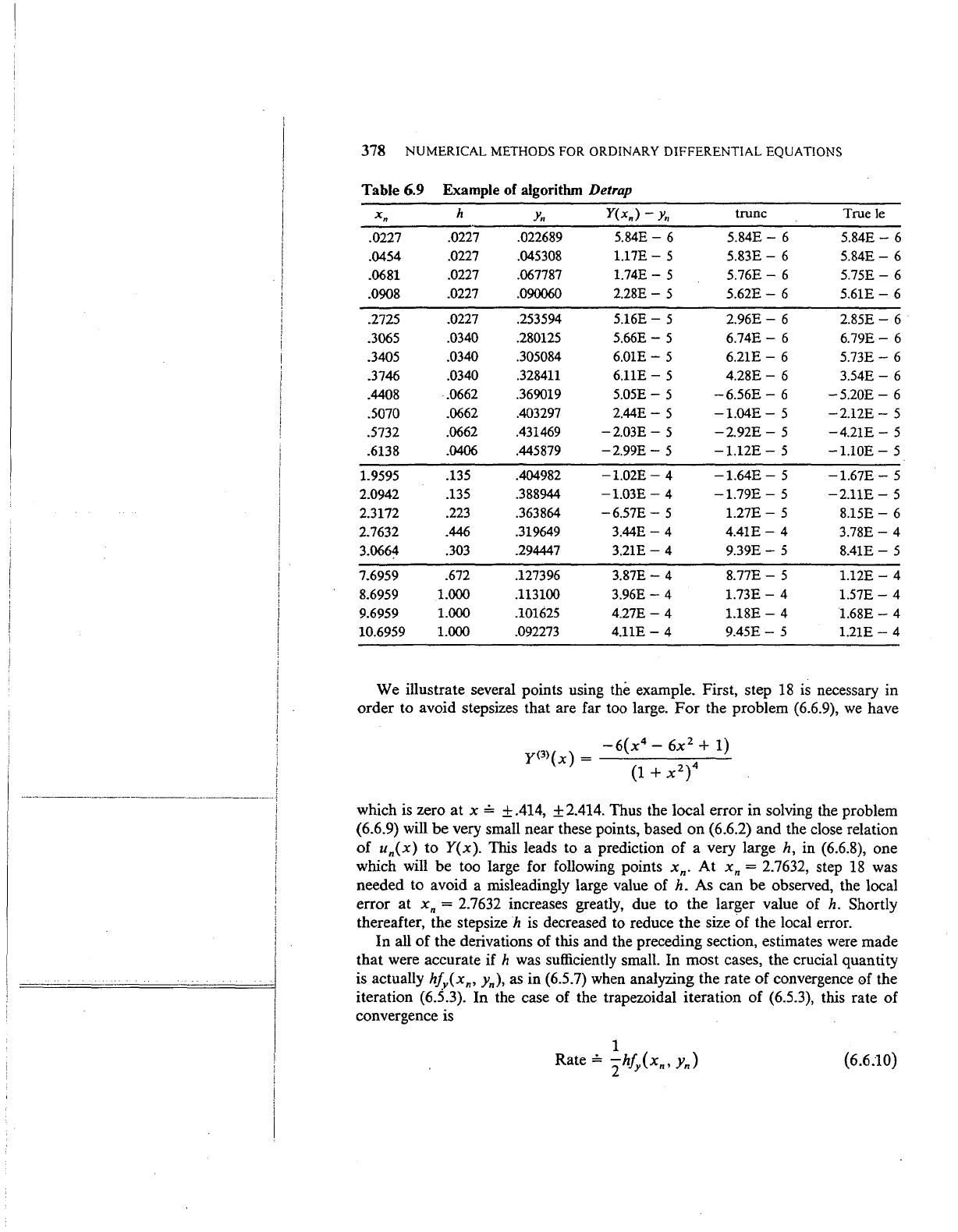
378

NUMERICAL

METHODS FOR ORDINARY

DIFFERENTIAL

EQUATIONS

Table 6.9

Example of algorithm Detrap

xn

h

Yn

Y(xn)-

Yn

trunc

True

Je

.0227

.0227 .022689

5.84E-

6

5.84E-

6

5.84E-

6

.0454

.0227

.045308

1.17E-

5

5.83E-

6

5.84E-

6

.0681

.0227 .067787

1.74E-

5

5.76E-

6

5.75E-

6

.0908

.0227 .090060

2.28E-

5

5.62E-

6

5.61E-

6

.2725

.0227 .253594

5.16E-

5

2.96E-

6

2.85E-

6

.3065

.0340

.280125

5.66E-

5

6.74E-

6

6.79E-

6

.3405

.0340 .305084

6.01E-

5

6.21E-

6

5.73E-

6

.3746

.0340 .328411

6.11E-

5

4.28E-

6

3.54E-

6

.4408

·.0662 .369019

5.05E-

5

-6.56E-

6

-5.20E-

6

.5070

.0662 .403297

2.44E-

5

-1.04E-5

-2.12E-

5

.5732

.0662 .431469

-2.03E-

5

-2.92E-

5

-4.21E-

5

.6138

.0406 .445879

-2.99E-

5

-1.12E-

5

-l.lOE-

5

1.9595

.135

.404982

-1.02E-

4

-1.64E-

5

-1.67E-

5

2.0942 .135

.388944

-1.03E-

4

-1.79E-

5

-2.11E-

5

2.3172

.223 .363864

-6.57E-

5

1.27E-

5

8.15E-

6

2.7632

.446 .319649

3.44E-

4

4.41E-

4

3.78E-

4

3.066~

.303 .294447

3.21E-

4

9.39E-

5

8.41E-

5

7.6959 .672 .127396

3.87E-

4

8.77E-

5

1.12E-

4

8.6959

1.000 .113100

3.96E-

4

1.73E-

4

1.57E-

4

9.6959

1.000

.101625

4.27E-

4

1.18E-

4

1.68E-

4

10.6959

1.000 .092273

4.11E-

4

9.45E-

5

1.21E-

4

We illustrate several points using the example. First, step

18

is

necessary in

order to avoid stepsizes that are far too large.

For

the problem (6.6.9),

we

have

which

is

zero

at

x

,;,

± .414, ± 2.414. Thus the local error in solving the problem

(6.6.9) will

be

very small near these points, based

on

(6.6.2) and the close relation

of

un(x)

to

Y(x).

This leads to a prediction of a very large

h,

in (6.6.8), one

which will

be

too large for following points

xn.

At

xn

= 2.7632, step

18

was

needed to avoid a misleadingly large value of

h. As can

be

observed, the local

error at

xn = 2.7632 increases greatly, due to the larger value of

h.

Shortly

thereafter, the stepsize

h

is

decreased to reduce the size of the local error.

In all

of

the derivations of this and the preceding section, estimates were made

that were accurate if

h

was

sufficiently small. In most cases, the crucial quantity

is actually

hfv(xn,

Yn),

as

in (6.5.7) when analyzing the rate of convergence

0f

the

iteration

(6.5.3).

In

the case of the trapezoidal iteration of (6.5.3), this rate of

convergence is

(6.6:10)

A LOW-ORDER PREDICTOR-CORRECTOR ALGORITHM 379

and for the problem (6.6.9), the rate

is

Rate=

-2hyn

If

this

is

near

1,

then

s_everal

iterations are necessary to obtain an accurate

estimate of

Yn+l·

From the table, the rate roughly increases in size

ash

increases.

At

xn = 2.3172, this rate

is

about .162. This still seems small enough, but the

local error

is

more inaccurate than previously, and this may be due· to a less

accurate iterate being obtained

in

(6.5.3). The algorithm can be made more

sophisticated in order to detect the problems

of

too large an

h,

but setting a

reasonably sized

h max

will

also help.

The global error

We

begin by

givi11g

an error bound analogous to the bound

(6.5.18) for a

fixed

stepsize. Write

For the last term,

we

assume the error per unit step criterion (6.6.1)

is

satisfied:

{6.6.12)

For the other term in (6.6.11), introduce the integral equation refqrmulations

Y(x)

=

Y(x,)

+

jxf(t,

Y(t))

dt

x.

un(x) =

Yn

+

jxf(t,

un(t)) dt

x.

Subtract and take bounds using the Lipschitz condition to obtain

I

Y(x)

- u,(x) I

:5

I

e,

I + K(x -

x,)

Max I

Y(t)

-

u,(i)

I

.m::=J::;x

with

en

= Y(xn) -

Yn·

Using this,

we

can derive

Introduce

H = Max

(xn+l-

xn)

=Max

h

x

0

sx.sb

and assume that

HK<l

Combining (6.6.11), (6.6.12),

and

(6.6.14),

we

obtain

1

len+ll

~

1

_ HKlenl +

€H

(6.6.13)

X

2:::

X,

(6.6.14)

i

·-------------------------------------------!

380 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS

This is easily solved, much

as

in Theorem 6.3, obtaining

[

ec(h-x

0

)

_

1]

jY(xn)-Ynl~ec<h-xolKjY(xo)-yol+

c.

€

(6.6.15)

for an appropriate constant c >

0.

This

is

the basic error result when using a

variable stepsize, and it is a partial justification

of

the error criterion (6.6.1).

In

some situations,

we

can obtain a more realistic bound.

For

simplicity,

assume

fv(x,

y)

~

0 for all

(x,

y).

Subtracting

in

(6.6.13),

Y(x)-

un(x)

=en+

jx[J(t,

Y(t))-

f(t,

un(t))]

dt

x.

The last step uses the mean-value theorem 1.2, and it can be shown that

Bf(t,

t(t))jBy

is a continuous function of t. This shows that

v(x)

=

Y(x)-

un(x) is a solution of the linear problem

'( )

Bf(x,

~(x))

( )

V X =

By

V X

The solution

of

this linear problem, along with the assumption fv(x,

y)

~

0,.

implies · -

jY(xn+l)-

un(xn+l)

I:::;;

lenl

The condition fy(x,

y)

~

0

is

associated with well-conditioned initial value

problems, as was noted earlier in (6.1.8).

Combining with (6.6.11) and (6.6.12),

we

obtain

jY(xn+l)-

Yn+ll

~jY(xn)-

Ynl

+

€(Xn+l-

xn)

Solving the inequality, we obtain the more realistic bound

(6.6.16)

This partially explains the good behavior of the example in Table 6.9; and even

better theoretical results are possible. But results

(6.6.15) and (6.6.16) are suffi-

cient justification for the use of the test (6.6.1), which controls the error per unit

step.

For

systems of equations y' = f(x,y), the condition fy(x,

y)

~

0 is replaced

by requiring

that

all eigenvalues of the Jacobian matrix fy(x, Y(x)) have real

parts that are zero

or

negative.

The algorithm

Detrap

could be improved

in

a number

of

ways. But it

illustrates the construction of a predictor-corrector algorithm with variable

stepsize.

The

output

is

printed at an inconvenient set

of

node points xn,

but

a

simple interpolation algorithm can take care

of

this. The predictors can

be

improved upon,

but

that too would make the algorithm more complicated.

In

the

next section, we return to a discussion

·of

currently available practical

predictor-corrector algorithms, most of which also vary the order.

Atkinson K. An Introduction to Numerical Analysis

Подождите немного. Документ загружается.