Atkinson K. An Introduction to Numerical Analysis
Подождите немного. Документ загружается.


\
·····---1
THE MIDPOINT METHOD 361
and
applying (6.3.8),
p
c = K L
!b)
j-
-1
The
right side
is
trivially a bound for /,., and thus
fn+l
~
/,. +
hc/,.+1
+
hT(h)
For
he
~
! , which must
be
true as h
_..
0,
~
(1
+ 2hc)/,. + 2h-r(h)
Noting that
fP
=
TJ(h),
proceed as in the proof
of
Theorem 6.3 following
(6.2.20). Then
[
e2c(b-xo)
-
1]
/,.
~
e2c(b-xo>TJ(h)
+ c -r(h)
x
0
~
x,.
~
b (6.3.19)
This completes the proof.
•
The
conclusions
of
the theorem
caa
be proved under weaker assumptions; in
particular, (6.3.17) can be replaced by a ·much weaker assumption. These results
are given
in
Section
6.8.
To
obtain a rate
of
convergence
of
O(hm)
for the
method (6.3.1),
it
is necessary that each step has
an
error
But the initial values y
0
,
•••
,
Yp
need to be computed with only
an
accuracy
of
O(hm),
since TJ(h) =
O(hm)
is sufficient in (6.3.18). Examples illustrating the use
of
a lower
order
method for generating the initial values y
0
,
•••
,
Yp
are given in
the following sections. ·
The
result (6.3.19) can be improved somewhat for particular cases,
but
the
speed
of
convergence
will
remain the same. Examples
of
the theorem are given in
the following sections.
As
with Euler's method, a complete stability analysis can
be given, including a result
of
the form (6.2.29). The proof is a straightforward
modification
of
the proof
of
Theorem 6.6. Also,
an
asymptotic error analysis can
be
given; examples are given in the next two sections.
6.4 The Midpoint Method
We will define
and
analyze the midpoint method, using it to illustrate some ideas
not possible with Euler's method. We can derive
the
midpoint method in several
ways, as with Euler's method,
and
we
use numerical differentiation here.

I
!
I
I
..
---··
___
.:
___
:
_____
j
362 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS
From (5.7.11) of Chapter
5,
we
have
g(
a
+h)-
g(a-
h)
h
2
g'(a) =
·-
-gP>(g)
2h 6
for some a - h
~
~
;:S;
a +
h.
Applying this to
Y'(x,)
=
J(x,,
Y(x,))
we
have
Y(x
) -
Y(x
) h
2
n+1
2h
n-1
- 6
yP>(~,)
=
J(x,,
Y(x,))
( 6.4.1)
The midpoint method
is
obtained by dropping the last term:
Yn+1
=
Yn-1
+ 2hj(x,.,
y,.)
n~1
(6.4.2)
It is an explicit two-step method, and the order
of
convergence is two. The value
of y
1
must
be
obtained by another method.
The midpoint method could also have been obtained by applying the midpoint
numerical integration rule (5.2.17) to the following integral reformulation of the
differential equation
(6.0.1):
Y(x,+l) =
Y(x,_
1
)
+
Jx".
1
j(t,
Y(t))
dt
x,_l
(6.4.3}
We omit the details. This approach
is
used in Section 6.7,
to
obtain other
multistep methods.
To analyze the convergence
of
(6.4.2),
we
use Theorem 6.6. From (6.4.1),
(6.3.4), (6.3.5), we easily obtain
that
( 6.4.4}
An
improved version of the proof of Theorem 6.6, for the midpoint method,
yields
( 6.4.5)

THE MIDPOINT METHOD 363
Assuming
y
0
= Y
0
for all
h,
we
need to have Y(x
1
)-
Yh(x
1
) = O(h
2
)
in
order to have a global order of convergence
O(h
2
)
in (6.4.5). From (6.2.4), a
single step
of
Euler's method has the desired property:
Yt
=Yo+
hf(xo,
Yo)
Yo=
Yo
(6.4.6)
(6.4.7)
With this initial value yh(x
1
) = y
1
,
the error result (6.4.5) implies
(6.4.8)
A complete stability analysis can be given for the midpoint method, parallel-
ing
that
given for Euler's method.
If
we
assume for simplicity that
71(h)
=
O(h
3
),
then we have the following asymptotic error formula:
Xo
~
Xn
~
b
(6.4.9)
There is little that
is
different in the proofs
of
these results, and
we
dispense with
them.
Weak stability As previously noted, the midpoint method possesses the same
type
of
stability as that shown for Euler's method
in
(6.2.28) and (6.2.29). This
is,
however, not sufficient for practical purposes. We show that the midpoint method
is unsatisfactory with respect to another sense
of
stability yet to be defined.
We consider the numerical solution
of
the problem
y'
= 'Ay
y(O)
= 1
(6.4.10)
which has the solution
Y(x)
=
eAx.
This
is
used as a model problem for the more
general problem
(6:0.1), an idea that
we
explain
in
Section 6.8. At this point, it
is
· sufficient to note that if a numerical method performs badly for a problem as
simple as
(6.4.10), then such a method is unlikely to perform well for other more
complicated differential equations.
The midpoint method for
(6.4.10) is
Yn+I
=
Yn-1
+
2h'J...yn
n~1
(6.4.11)
We calculate the exact solution
of
this equation
and
compare
it
to the solution
Y(x)
=
e>..x.
The
equation (6.4.11) is an example
of
a linear difference equation
of
order
2.
There is a general theory for
pth-order
linear difference equations,
paralleling the theory for pth-order linear differential equations. Most methods
for solving the differential equations have
an
analogue in solving difference
equations, and this
is
a guide in solving (6.4.11).
We
begin by looking for linearly
independent solutions
of
the difference equation. These are then combined to

i
i
I
I
I
J
364 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS
form the general solution. For a general theory of linear difference equations, see
Henrici (1962, pp. 210-215).
In analogy with the exponential solutions of linear differential equations,
we
assume a solution for (6.4.11) of the form
n?:.O
(6.4.12)
for some unknown
r.
su·bstituting into (6.4.11) to find necessary conditions on
r,
Canceling r
n-
1
,
r
2
= 1 + 2h'Ar (6.4.13)
This argument
is
reversible.
If
r satisfies the quadratic equation (6.4.13), then
(6.4.12) satisfies (6.4.11).
The equation (6.4.13)
is
called the characteristic equation for the midpoint
method. Its roots are
(6.4.14)
The general solution to (6.4.11)
is
then
n?:.O
(6.4.15)
The coefficients
/3
0
and
/3
1
are chosen so that the values of
Yo
and y
1
that were
given originally will agree with the values calculated using (6.4.15):
The general solution
is
f3
_
Yt-
r1Yo
o-
ro-
rl
To gain some intuition for these formulas, consider taking the exact initial
values
Yo= 1
Then using Taylor's theorem,
(6.4.16)

THE
MIDPOINT METHOD 365
From these values,
/3
0
~
1 and
/3
1
~ 0
as
h
~
0.
Therefore in the formula
(6.4.15), the term
f3
0
r
0
n
should correspond to the true solution e>.x., since the term
/3
1
rt
~
0 as h
~
0.
In fact,
(6.4.17)
whose proof we leave to the reader.
To
see
the difficulty in the numerical solution of
y'
=
AY
using (6.4.15),
examine carefully the relative sizes of r
0
and r
1
•
We consider only the case of real
A.
For
0 < A <
oo,
for all h,
Thus the term r
1
n
wili
increase less rapidly than r
0
n,
and the correct term in the
general solution
(6.4.15) will dominate, namely
f3
0
r
0
.
However,. for -
oo
< A <
0,
we
will
have
0 < r
0
< 1
h>O
As a consequence,
/3
1
r
1
n will eventually dominate
f3
0
r
0
nas
n increases, for fixed h,
no matter how small h
is
chosen initially. The term
f3
0
r
0
n
~
0 as n
~
oo;
whereas, the term
f3
1
rt
increases in magnitude, alternating in sign
as
n increases.
The term
/3
1
rt
is
called a parasitic solution of the numerical method (6.4.11),
since it does
not
correspond to any solution of the original differential equation
y'
= Ay. This original equation has a one-parameter family of solutions, depend-
ing on the initial value
Y
0
,
but the approximation (6.4.11) has the two-parameter
family
(6.4.15), which
is
dependent on y
0
and Y!· The new solution
f3
1
rt
is a
creation of the numerical method; for problem
(6.4.10) with A <
0,
it will cause
the numerical solution to diverge from the true solution
as
xn
~
oo.
Because of
this behavior,
we
say that the midpoint method is only weakly stable.
We return to this topic in Section
6.8,
after some necessary theory has been
introduced. We generalize the applicability of the model problem
(6.4.10) by
considering the sign of
aj(x,
Y(x))/
a
y.
If
it
is
negative, then the weak instability
of the midpoint method will
usmilly appear in solving the associated initial value
problem. This
is
illustrated in the second example below.
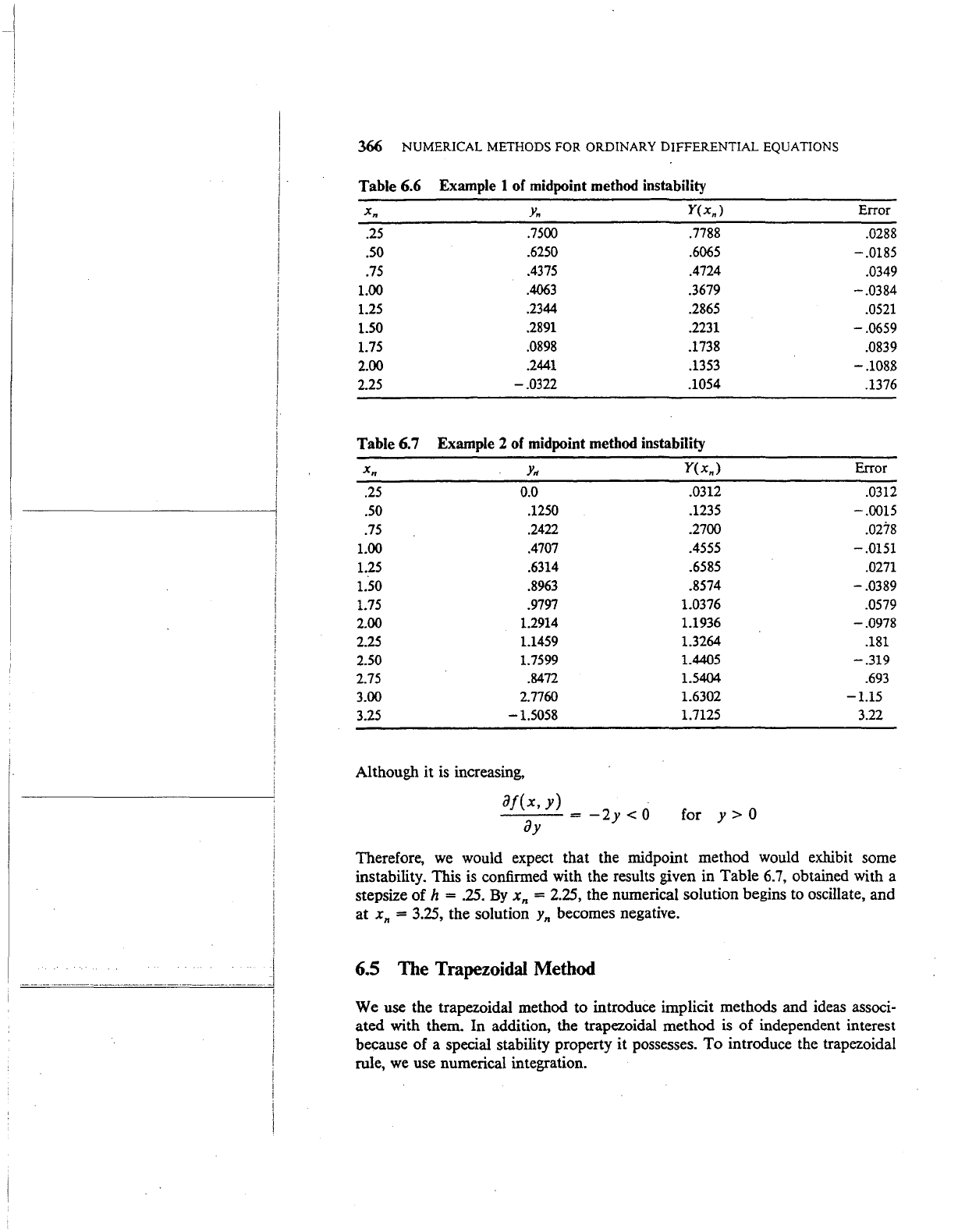
Example
1.
Consider the model problem (6.4.10) with
A=
-1.
The numerical
results are given in Table
6.6 for h = ..
25.
The value y
1
was obtained using
Euler's method, as in
(6.4.6). From the values in the table, the parasitic solution
is
clearly growing in magnitude. For xn =
2.25,
the numerical solution
Yn
becomes
negative,
and
it alternates in sign with each successive step.
2. Consider the problem
y'
=X-
y2
y(O)
= 0
The solution
¥(x)
is
strictly increasing for x;::: 0; for large
x,
Y(x)
=
/X.
I
I
I
---
---
-
..
I
I
I
I
I
!
i
I
I
!
366
NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS
Table 6.6
Example 1 of midpoint method instability
Xn
Yn
Y(xn)
Error
.25
.7500
.7788
.0288
.50
.6250 .6065
-.0185
.75
.4375 .4724
.0349
1.00
.4063
.3679
-.0384
1.25
.2344
.2865
.0521
1.50
.2891
.2231
-.0659
1.75
.0898
.1738
.0839
2.00
.2441
.1353 -.108.8
2.25
-.0322
.1054
.1376
Table 6.7
Example 2 of midpoint method instability
Xn
Yn
Y(xn)
Error
.25
0.0
.0312
.0312
.50
.1250
.1235
-.0015
.75
.2422 .2700
.0278
1.00
.4707
.4555
-.0151
1.25
.6314
.6585
.0271
1.50
.8963
.8574
-.0389
1.75
.9797
1.0376 .0579
2.00
1.2914
1.1936
-.0978
2.25
1.1459
1.3264
.181
2.50
1.7599
1.4405
-.319
2.75
.8472
1.5404
.693
3.00
2.7760
1.6302
-1.15
3.25
-1.5058
1.7125 3.22
Although it
is
increasing,
aj(x,y)
=
-2y
< 0
ay
for
y>O
Therefore,
we
would expect that the midpoint method would exhibit some
instability. This
is
confirmed with the results given in Table 6.7, obtained with a
stepsize of
h =
.25.
By
xn
= 2.25, the numerical solution begins to oscillate, and
at
xn
= 3.25, the solution
Yn
becomes negative.
6.5 The Trapezoidal Method
We use the trapezoidal method to introduce implicit methods and ideas associ-
ated with them. In addition, the trapezoidal method is
of
independent interest
because of a special stability property it possesses.
To
introduce the trapezoidal
rule,
we
use numerical integration.

THE
TRAPEZOIDAL METHOD
367
Integrate the differential equation
Y'(t)
=
f(t,
Y(t)) over [xn, xn+ll to obtain
Y(xn+l)
=
Y(xJ
+ Jxn+lf(t,
Y(t))
dt
.
x.
Apply the simple trapezoidal rule, (5.1.2) and (5.1.4), to obtain
(6.5.1)
for some xn
~
gn
~
xn+l·
By
dropping the remainder term, we obtain the
trapezoidal method,
h
Yn+l
=
Yn
+
2[/(xn,
Yn)
+
f(xn+l•
Yn+l)]
n;;:::O
(6.5.2)
It
is a one-step method with an O(h
2
)
order of convergence.
It
is also a simple
example
of
an implicit method, since
Yn+l
occurs
on
both sides of (6.5.2). A
numerical example
is
given at the end of this section.
Iterative solution The formula
(6.5.2) is a nonlinear equation with root
Yn+l•
and
any
of
the general techniques of Chapter 2 can
be
used to solve it. Simple
linear iteration (see Section
2.5) is most convenient
and
it
is usually sufficient. Let
y~2
1
be
a good initial guess of the solution
Yn+l•
and
define
(j+l)
- + h
[!(
) +
!(
(j)
)]
Yn+l
-
Yn
2
Xn,
Y,;
Xn+l•
Yn+l
j = 0,
1,...
(6.5.3)
The
initial guess
is
usually obtained using an explicit method.
To
analyze the iteration and to determine conditions under which it will
converge, subtract
(6.5.3) from (6.5.2) to obtain
h
Y
·
-
yU+I>
= -
[f(x
y ) -
f(x
yU>
)]
n+l
n+l
2 n+l• n+l n+l• n+l
Use the Lipschitz condition (6.2.12) to bound this
with
If
.
hK
.
'y
-y<J+l>i
<
-ly
-
<J>
I
n+l n+l - 2 n+l
Yn+l
hK
-<1
2
(6.5.4)
(6.5.5)
(6.5.6)
then the iterates
y~{\
will
converge to
Yn+l
as
j ~ oo. A more precise estimate

i
i
- ------·
----...
_\
368 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS
of the· convergence rate
is
obtained ·from applying the mean value theorem to
(6.5.4):
h
(j
+ 1)
..:..
/,
( ) [
(j)
]
Yn+l-
Yn+l - 2 y Xn+l• Yn+l
Yn+l-
Yn+l
(6.5.7)
Often in practice, the stepsize h and the initial guess
y~~
1
are chosen to ensure
that only one iterate need be computed, and then
we
take Yn+l
.,;,
y;~
1
•
The
computation of Yn+l from
Yn
contains a truncation error that
is
O(h
3
)
[see (6.5.1)].
To
maintain this order of accuracy, the eventual iterate
y~2
1
,
which
is
chosen to represent Yn+l• should satisfy
IYn+l
-
Y~2d
= O(h
3
).
And if
we
· want the iteration error to be less significant (as
we
do in the next section), then
y~2
1
should be chosen to satisfy
(6.5.8)
To analyze the error in choosing an initial guess Yn+l•
we
must introduce the
concept of
local solution. This will also be important in clarifying exactly what
solution
is
being obtained by most automatic computer programs for solving
ordinary differential equations. Let
un(x)
denote the solution of
y'
=
j(x,
y)
that passes through
(xn,
Yn):
u~(x)
=
f(x,
un(x))
(6.5.9)
At step xn, knowing
Yn'
it
is
un(xn+l)
that
we
are trying to calculate, rather than
Y(xn+l).
Applying the derivation that led to (6.5.1),
we
have
for some
Xn:::;;
gn:::;;
xn+l·
Let
en+l
=
un(Xn+l)-
Yn+l>
which
we
call the local
error
in computing Yn+l from
Yn·
Subtract (6.5.2) from the preceding to obtain
h h
3
en+l
= 2
[/(xn+l•
un(xn+l))
-
f(xn+l•
Yn+l)] -
l2
u~
3
>an)
where
we
have twice applied the mean value theorem.
It
can
be
shown that for all
sufficiently small
h,

THE
TRAPEZOIDAL METHOD
369
This shows that the local error is essentially the truncation error.
If
Euler's method is used to compute
y~~
1
,
then un(xn+
1
) can be expanded to show that
h2
(
)
(0) -
"(,.
)
un
xn+1
-
Yn+1-
Tun
!ln
Combined with (6.5.11),
Y
-
y<O>
=
O(h2)
n+1 n+1
(6.5.11)
(6.5.12)
(6.5.13)
(6.5.14)
To satisfy (6.5.8), the bound (6.5.5) implies two iterates
will
have to be computed,
and then we use
y~~
1
to represent
Yn+
1
.
Using
the midpoint method,
we
can obtain the more accurate initial guess
(6.5.15)
To estimate the error, begin by using the derivation that leads to (6.4.1) to
obtain
- ( )
h3
(3)(
un(xn+
1
)-
un(xn-1) +
2hj
Xn,
un(xn)
+
3
Un
'11n),
for some xn-1 ;5;
"11n
;5;
xn+1·
Subtracting (6.5.15),
. h3
un(xn+1)-
Y~~1
=
un(xn-1)-
Yn-1 +
3U~
3
>('11n)
The quantity un(xn_
1
) - Yn-l·can be computed
in
a manner similar to that used
for (6.5.11) with about the same result:
h3
un(xn-1)-
Yn-1
=
12
U~
3
>(xn)
+ O(h
4
)
(6.5.16)
Then
5h
3
u
(x
) -
y<O>
=
-u<
3
>(x
) +
O(h
4
)
n
n+1
n+1
12 n n
And
combining this with (6.5.11),
h3
Y
-
y<
0
> =
-u<
3
>(x
) +
O(h
4
)
n+1
n+1
2 n n
(6.5.17)

i
1
I
I
I
____
_J
370 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS
With the initial guess (6.5.15), one iterate from (6.5.3)
will
be sufficient to satisfy
(6.5.8), based on the bound in (6.5.5).
The formulas (6.5.12) and (6.5.15) are called
predictor formulas, and the
trapezoidal iteration formula (6.5.3)
is
called a corrector formula. Together they
foi:m
a predictor-corrector method, and they are the basis of a method that can
be used to control the size of the local error. This is illustrated in the next section.
Convergence and stability results The convergence of the trapezoidal method
is
assured
by
Theorem
6.6.
Assuming
hk
.:s:;
1,
Max
IY(xn) - Yh(xn)
l.:s:;
eZK(b-:co>leol
:c
0
;S;:c.s;b
The derivation of an asymptotic error formula
is
similar to that for Euler's
method. Assuming
e
0
= 5
0
h
2
+
O(h
3
),
we
can show
(6.5.19)
The standard type of stability result, such as that given in
(6.2.28) and (6.2.29) for
Euler's method,
can also be given for the trapezoidal method. We leave the proof
of
this to the reader.
As with the midpoint method,
we
can examine the effect of applying the
trapezoidal rule to the model equation
y'
=
A.y
y(O)
= 1
(6.5.20)
whos~
solution
is
Y(x)
=
e>.x_
To
give further motivation for doing so, consider
the
trapezol.dal method applied to the linear equation
y'=A.y+g(x)
y(O)
= Y
0
(6.5.21)
namely
h
Yn+l
=
Yn
+ 2
[A.yn
+ g(xn) +
AYn+l
+ g{xn+l)]
n
~
0 (6.5.22)
with
Yo= Then consider the perturbed numerical method
h
Zn+l
=
Zn
+ 2
[A.zn
+
g(xn)
+
AZn+l
+ g{xn+l)]
n~O
