Atkinson K. An Introduction to Numerical Analysis
Подождите немного. Документ загружается.


DERIVATION OF HIGHER
ORDER
MULTISTEP METHODS 391
In the program DE of Shampine and Gordon (1985, 186-209), the truncation
error at
xn+l [call it trunc]
is
required to satisfy
jtruncjj
::::;;
ABSERR + RELERR*
IYn)
(6.7.30)
This
is
to hold for each component of the truncation error and for each
corresponding component
Yn,
j of the solution
Yn
of the given system of differen-
tial equations. The values
ABSERR and RELERR are supplied by the user. The
value of trunc
is
given, roughly speaking, by
t
-'-hl.'
'l"'7p+l'
rune-
~p+lv
Yn+l
assuming the spacing
is
uniform. This
is
the truncation error for the p-step
formula
p
Y~!i
=
Yn
+ h L
8pjy~+l
j=O
Once the test (6.7.30)
is
satisfied, the value of
Yn+l
is
Yn+l
=
Y~!i
1
>
=
Y~!l
+ trunc
(6.7.31)
Thus the actual truncation error
is
O(hP+
3
),
and combined with (6.7.30), it can
be shown that the truncation error in
Yn+l
satisfies an error per unit step criteria,
which
is
similar to that of (6.6.1) for the algorithm Detrap of Section 6.6. For a
detailed discussion, see Shampine and Gordon
(1975, p. 100).
The program
DE
(and its successor DDEABM)
is
very sophisticated in its
error control, including the choosing of the order and the stepsize. It cannot be
discussed adequately in the limited space available in this text, but the best
reference is the text of
Shampine and Gordon (1975), which
is
devoted to
variable-order Adams algorithms. The
programs
DE
and DDEABM have been
well
designed .from both the viewpoint of error control and user convenience.
Each
is
also written in a portable form, and generally,
is
a well-recommended
program for solving differential equations.
Example Consider the problem
which has the solution
y(O)
= 1
20
Y(x)=
-----
(1
+ 19e-<xf
4
l)
·
(6.7.32)
DDEABM was used to solve this problem with values output
at
x =
2,
4,
6,
...
, 20.
Three values of. ABSERR were used, and
RELERR
= 0
in
all cases. The true
global errors are shown in Table
6.15. The column labeled
NFE
gives the number
of evaluations of
f(x,
y)
necessary to obtain the value
yh(x),
beginning from x
0
.

i
'
-·-··-
---·--·---------------------------------------···---------l
'
392 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS
Table 6.15
Example of the automatic program DDEABM
ABSERR =
10-
3
ABSERR =
10
6
ABSERR =
10
9
X
Error
NFE Error
NFE
Error
NFE
4.0
-3.26E-
5
15
1.24E-
6
28
2.86E-
10
52
8.0
6.00E-
4
21
3.86E-
6
42
-1.98E-
9
76
12.0
1.70E-
3
25
4.93E-
6
54
-2.41E-
9
102
16.0
9.13E-
4
31
3.73E-
6
64
-l.86E-
9
124
20.0
9.16E-
4
37
1.79E-
6
74
-9.58E-
10
138
Global error The automatic computer codes that are discussed previously
control the local error or truncation error. They
do
not control the global error in
the solution.
Usually the truncation error is kept so small by these codes that the
global error is also within acceptable limits, although that is not guaranteed. The
reasons for this small global error are much the same as those described in
Section 6.6; in particular, recall (6.6.15) and (6.6.16).
The
global error can be monitored, and we give an example of this below. But
even with
an
estimate of the global error,
we
cannot control it for most equations.
This is because the global error
is
composed
of
the effects
of
all past truncation
errors,
and
decreasing the present stepsize will
not
change those past errors. In
general,
if
the global error is too large, then the equation must be solved again,
with a smaller stepsize.
There are a number of methods that have been proposed for monitoring the
global error.
One of these, Richardson extrapolation, is illustrated in Section 6.10
for a
Runge-Kutta
method. Below, we illustrate another one for the method
of
Section 6.6.
For
a general survey
of
the topic, see Skeel (1986).
For
the trapezoidal method, the true solution
Y(x)
satisfies
with
h =
Xn+l
-
Xn
and
xn
~
~n
~
xn+l· Subtracting the trapezoidal rule
h
Yn+l
=
Yn
+ 2
[J(xn,
Yn)
+
f(xn+l•
Yn+I)]
we have
h
en+l
=en+
2 {
[J(xn,
Yn
+en)-
f(xn,
Yn)]
h3
+ [/(xn+I•
Yn+l
+
ei>+I)
- f(xn+l•
Yn+I)]}
-
12
Y(3)(~n)
(6.7.33)
with
en
= Y(xn) -
Yn•
n
~
0.
This is the error equation for the trapezoidal
method,
and
we try to solve it approximately in order to calculate
en+
I·
DERIVATION
OF
HIGHER ORDER MULTISTEP METHODS
393
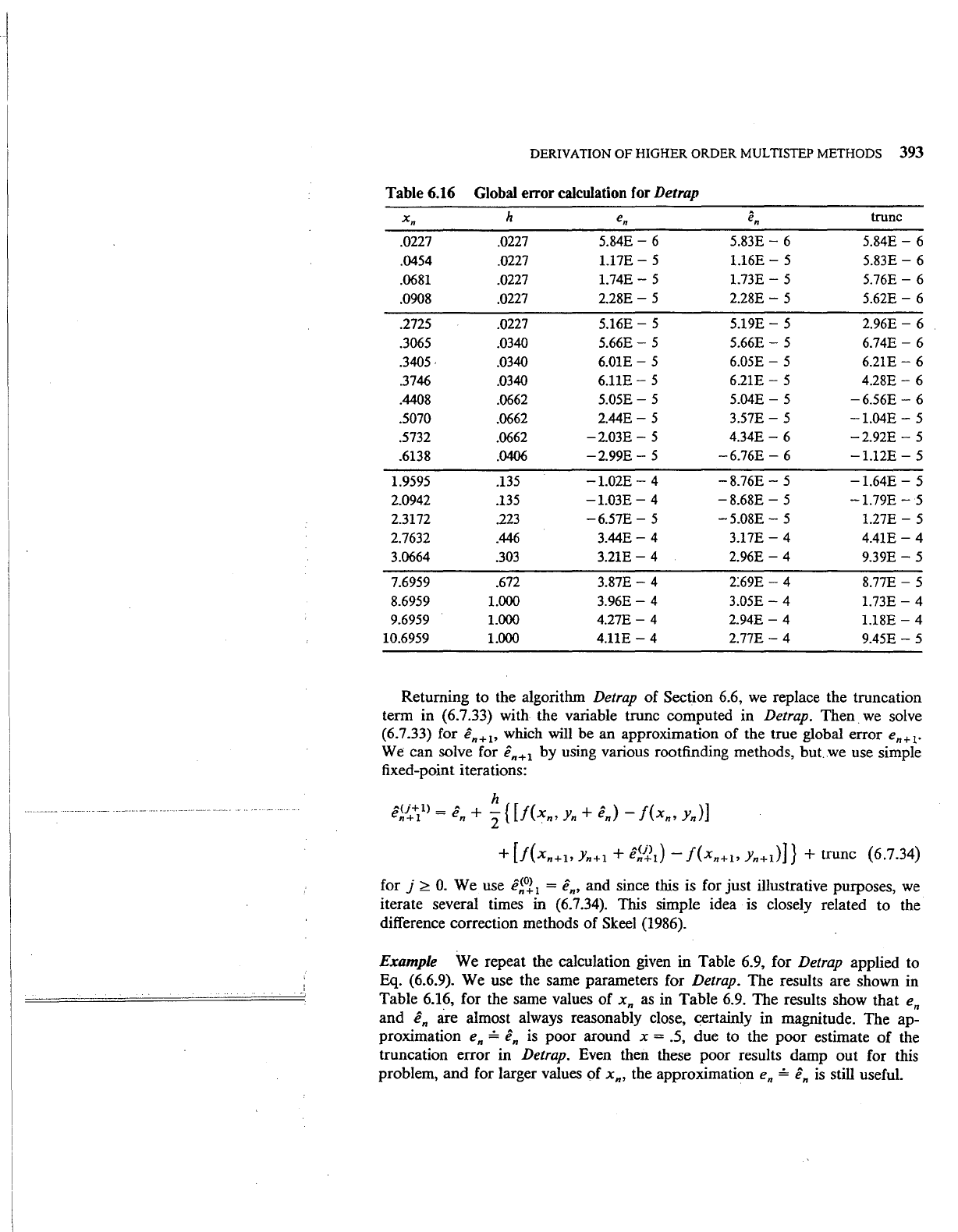
Table 6.16 Global error calculation for Detrap
xn
h
en
en
trunc
.0227
.0227
5.84E-
6
5.83E-
6
5.84E-
6
.0454 .0227
1.17E-
5
1.16E-
5
5.83E-
6
.0681
.0227
1.74E-
5
1.73E-
5
5.76E-
6
.0908
.0227
2.28E-
5
2.28E-
5
5.62E-
6
.2725
.0227
5.16E-
5
5.19E-
5
2.96E-
6
.3065
.0340
5.66E-
5
5.66E-
5
6.74E-
6
.3405'
.0340
6.01E-
5
6.05E-
5
6.21E-
6
.3746
.0340
6.11E-
5
6.21E-
5
4.28E-
6
.4408
.0662
5.05E-
5
5.04E-
5
-6.56E-
6
.5070 .0662
2.44E-
5
3.57E-
5
-1.04E-
5
.5732
.0662
-2.03E-
5
4.34E-
6
-2.92E-
5
.6138
.0406
-2.99E-
5
-6.76E-
6
-1.12E-
5
1.9595
.135
-L02E-
4
-8.76E-5
-1.64E-
5
2.0942
.135
-1.03E-
4
-8.68E-
5
-1.79E-
5
2.3172
.223
-6.57E-
5
-5.08E-
5
1.27E-
5
2.7632
.446
3.44E-
4
3.17E-
4
4.41E-
4
3.0664
.303
3.21E-
4
2.96E-
4
9.39E-
5
7.6959
.672
3.87E-
4
2:69E-
4
8.77E-
5
8.6959
1.000
3.96E-
4
3.05E-
4
1.73E-
4
9.6959
1.000
4.27E-
4
2.94E-
4
1.18E-
4
10.6959 1.000
4.11E-
4
2.77E-
4
9.45E-
5
Returning to the algorithm Detrap of Section 6.6,
we
replace the truncation
term in (6.7.33) with the variable trunc computed in
Detrap. Then.
we
solve
(6.7.33) for en+l• which will be an approximation of the true global error en+l·
We can solve for en+l by using various rootfinding methods, but..we use simple
fixed-point iterations:
h
A{j+l)-
A
-{[/(
+A)-!(
)]
en+l -
en+
2
xn,
Yn
en
xn,
Yn
+
[f(xn+I•
Yn+I
+
e!.iJr)-
f(xn+l•
Yn+I)]}
+ trunc (6.7.34)
for
j
;:::::
0.
we
use
e!OJ.r
= e n• and since this is for
just
illustrative purposes,
we
iterate several times in (6.7.34). This simple idea is closely related to the
difference correction methods of Skeel (1986).
Example
We repeat the calculation given in Table 6.9, for Detrap applied to
Eq. (6.6.9). We use the same parameters for Detrap. The results are shown in
Table 6.16, for the same values of
xn
as
in Table
6.9.
The results show that
en
and en are almost always reasonably close, c:ertainly in magnitude. The ap-
proximation
en~
en
is
poor around
X=
.5, due
tO
the poor estimate
of
the
truncation error in
Detrap. Even then these poor results damp out for this
problem, and for larger values of
xn, the approximation
en
~
en
is
still useful.

394 NUMERICAL METHODS
FOR
ORDINARY DIFFERENTIAL EQUATIONS
6.8 Convergence
and
Stability Theory
for Multistep Methods
In
this section, a complete theory of convergence and stability
is
presented for
the multistep method
p p
Yn+l
= L ajYn-j + h L
bjf(xn-j•
Yn-j)
Xp+l
~
Xn+I
~
b (6.8.1)
j=O
j=
-1
This generalizes the work of Section 6.3, and it creates the mathematical tools
necessary for analyzing whether method
(6.8.1) is only weakly stable, due to
instability of the type associated with the midpoint method.
We begin with a
few
definitions. The concept of stability was introduced with
Euler's method
[see
(6.2.28) and (6.2.20)], and it is now generalized. Let
{YniO
~
n
~
N(h)} be the solution of (6.8.1) for some differential equation
y'
=
f(x,
y),
for all sufficiently small values of
h,
say h
~
h
0
.
Recall that
N(h)
denotes the
largest subscript
N for which
xN
~b.
For each h
~
h
0
,
perturb the initial values
y
0
,
•••
,
Yi>
to new values z
0
,
••
• , z P with
Max
IYn
-
znl
~
£
05,n5,p
0 < h
~
h
0
(6.8.2)
Note that these initial values are likely
to
depend on h. We say the family of
solutions {
Yn
I 0
~
n
~
N(
h)}
is stable if there is a constant
c,
independent of .
h
~
h
0
and valid
for
all sufficiently small
£,
for which
Max
IYn
-
zni
.~
C£
05.n5.N(h)
Consider all differential equation problems
y'
=
f(x,
y)
0 < h
~
h
0
(6.8.3)
( 6.8.4)
with the derivative
f(x,
y)
continuous and satisfying the Lipschitz condition
(6.2.12), and suppose the approximating solutions {
Yn}
are all stable. Then
we
say that (6.8.1)
is
a stable numerical method.
To define convergence for a given problem (6.8.4), suppose the initial values
y
0
,
•••
,
Yp
satisfy
(6.8.5)
Then the solution {
Yn
}
is
said to converge to Y(
x)
if
Max
IY(xn)-
Yni
~
0
x
0
5.x.5.b
·
(6.8.6)
If
(6.8.1) is convergent for all problems (6.8.4), then it is called a convergent
numerical method.

CONVERGENCE AND STABILITY THEORY
FOR
MULTISTEP METHODS 395
Recall the definition of consistency given in Section
6.3. Method (6.8.1)
is
consistent if
as
h
--"
0
for all functions
Y(x)
continuously differentiable
on
[x
0
,
b].
Or
equivalently from
Theorem 6.5,
the
coefficients
{a
j} and { bj} must satisfy
p p
-
I:
ja
j +
I:
bj = 1
(6.8.7)
j=O
j=
-1
Convergence
can
be
shown to imply consistency; consequently, we consider only
methods satisfying
(6.8.7). As an example
of
the
proof
of
the necessity
of
(6.8.7),
tl_le
assumption
of
convergence
of
(6.8.1) for the
problem
y'
= 0
y(O)
= 1
will imply the first condition in (6.8.7). Just take y
0
= · · · =
Yp
= 1, and observe
the
consequences
of
the convergence
of
Yp+l
to
Y(x)
=
1.
The
convergence and stability of (6.8.1)
are
linked to the roots of the
polynomial
p
p(r)
=
rp+l-
L
ajrp-j
j=O
(6.8.8)
Note
that p(1) = 0 from the consistency condition (6.8.7). Let r
0
,
•••
,
rP
denote
the roots
of
p(r),
repeated according to their multiplicity,
and
let r
0
=
1.
The
method (6.8.1) satisfies the root condition if
1.
2.
j =
0,
1,
...
, p
l'jl = 1 = p'(lj) * 0
(6.8.9)
(6.8.10)
The
first condition requires all roots
of
p(r)
to lie
in
the
unit circle {z:
lzl
~
1}
in the complex plane. Condition
(6.8.10) states
that
all roots
on
the boundary
of
the circle
are
to
be
simple roots
of
p(r).
-
The
main results of this section are pictured
in
Figure 6.6, although some
of
them will
not
be
proved. The strong root condition
and
the concept of relative
stability
are introduced later in the section.
Strong root
==::::;>
Relative
condition
stability
n
~
Convergence
~
Root
~
Stability
c.ondition
Figure
6.6 Schematic
of
the theory for con-
sistent multistep methods.

---------···-------------------------
----------------·----!
396
NUMERICAL
METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS
Stability theory
All
of the numerical methods presented in the preceding
sections have been stable, but
we
now
give
an example of an unstable method.
This is to motivate the need to develop a general theory of stability.
Exampk
Recall the general formula (6.7.10) for an explicit two-step second-
order method, and choose
a
0
=
3.
Then
we
obtain the method
h
Yn+l
=
3yn-
2Yn-l +
l[J(xn,
Yn)-
3/{xn-1• Yn-JJ
n
~
1 {6.8.11)
with the truncation error
Consider solving the
problemy'=
0,
y(O)
=
0,
which has the solution Y(x) =
0.
Using y
0
= y
1
=
0,
the numerical solution is clearly
Yn
= 0, n
~
0. Perturb the
initial
data
to z
0
= £/2, z
1
=
£,
for some £
'*
0. Then the corresponding numeri-
, cal solution can be shown to be
n~O
(6.8.12)
The. reasoning used in deriving this solution
is
given later in a more general
context. To see the effect of the perturbation on the original solution,
Max IYn-
Znl
= Max l£12n-l = I£12N(h)-l
~~~~h
o~~~h
Since
N(h)--+
oo
ash--+
0,
the deviation of {zn} from
{Yn}
becomes increas-
ingly greater as
h
--+
0.
The method (6.8.11)
is
unstable, and it should never be
used. Also note that the root condition is violated, since
p(r)
= r
2
-
3r
+ 2 has
the roots
r
0
= 1, r
1
=
2.
To
investigate the stability of (6.8.1),
we
consider only the special equation
y'
=]\y
y(O)
= 1 (6.8.13)
with the solution Y(x) =
e'hx.
The results obtained will transfer to the study of
stability for a general differential equation problem. An intuitive reason for this
is
easily derived. Expand Y'(x) =
f(x,
Y(x)) about
(x
0
,
Y
0
)
to obtain
=
A(Y{x)-
Y
0
)
+
g(x)
( 6.8.14)
with
A=
fy(x
0
,
Y
0
)
and
g(x)
=
f(x
0
,
Y
0
)
+
f;x(x
0
,
Y
0
)(x-
x
0
).
This
is
a valid
approximation if
x-
x
0
is
sufficiently small. Introducing
V(x)
=
Y(x)-
Y
0
,
V'(x) =
AV(x)
+
g(x)
(6.8.15)
The
inhomogeneous term
g(x)
will drop out of all derivations concerning

CONVERGENCE AND STABILITY THEORY FOR MULTISTEP METHODS 397
numerical stability, because we are concerned with differences of solutions of the
equation. Dropping
g(x)
in (6.8.15),
we
obtain the model equation (6.8.13). As
further motivation, refer back
to
the stability results (6.1.5)-(6.1.10),
and
to the
trapezoidal stability results in (6.5.20)-(6.5.23).
In
the case that
y'
= f(x,
y)
represents a system of m differentiable equations,
as in (6.1.13), the partial derivative
fy(x,y) becomes a Jacobian matrix,
at;
[ry(x,y)]
ij
=
-a
Y·
. 1
1:;;;
i,
j:;;; m
as
in
(6.2.54). Thus the model equation becomes
y'
=
Ay
+ g(x)
(6.8.16)
a·
system
of
m linear differential equations with A = f
y(x
0
,
Y
0
).
It
can be shown
that
in most cases, this system reduces to an equivalent system
z;
=
A;Z;
+ Y;(x)
(6.8.17)
with A
1
,
...
,
Am
the eigenvalues
of
A (see Problem 24).
With
(6.8.17), we are
back
to
the
simple model equation (6.8.13), provided we allow A to be complex
in
order
to include all possible eigenvalues of A.
Applying (6.8.1) to
the
model equation (6.8.13), we
obtain
p p
Yn+l
= L
ajYn-j
+ hA L hjYn-j
j=O
j=
-1
p
(1-
hAb_l)Yn+l-
L
(aj
+
hAbj)Yn-j
= 0
j=O
(6.8.18)
n~p
(6.8.19)
This
is a homogeneous linear difference equation
of
order
p + 1,
and
the theory
for its solvability is completely analogous to
that
of
(p
+ 1)st-order homoge-
neous linear differential equations. As a general reference, see Henrici (1962,
pp.
210-215)
or
Isaacson
and
Keller (1966, pp. 405-417).
We
attempt
to find a general solution
by
first looking for solutions
of
the
special form
n~O
If
we can find p + 1 linearly independent solutions, then
an
arbitrary linear
combination will give
the
general solution
of
(6.8.19).
Substituting
Yn
= rn
into
(6.8.19)
and
canceling
rn-p,
we obtain
p
(1-
hAb_
1
)rp+l-
L
(aj
+
hAbJrp-j
= 0
j=O
(6.8.20)
This
is called the characteristic equation, and the left-hand side is the characteris-

i
!
I
i
j
!
·-
·------·---·-·-·-·----·----------·-·--·-----------·
.!
I
.I
398
NUMERICAL
METHODS
FOR
ORDINARY DIFFERENTIAL EQUATIONS
iic polynomial. The roots are called characteristic roots. Define
p
a(r)
=
b_
1
rp+I + L b
1
rrl
j=O
and recall the definition (6.8.8)
of
p(r). Then (6.8.20) becomes
p(r}-
hA.a(r} = 0
Denote
the characteristic roots by
(6.8.21)
which
can
be
shown to depend continuously
on
the value of
hA..
When
hA.
=
0,
the equation (6.8.21) becomes simply
p(r)
= 0, and
we
have
r/0)
= r
1
,
j =
0,
1,
...
,
p,
for the earlier roots
1j
of
p(r)
= 0. Since r
0
= 1
is
a root of p(r),
we
let r
0
(hA.)
be
the root
of
(6.8.21) for which r
0
(0) =
1.
The root r
0
(hA.)
is
called
the principal root, for reasons
that
will become apparent later.
If
the roots r.(hA.)
are all distinct, then the general solution of (6.8.19)
is
1
p
Yn
= L
"Yjh(hA.)]
n
n;;::O
(6.8.22}
j=O
But if 'j(h"A) is a root
of
multiplicity P > 1, then the following are v linearly
independent solutions of
(6.8.19):
These can
be
used with the solution arising from the other roots to generate a
general solution for
(6.8.19), comparable to (6.8.22).
Theorem 6.7 Assume the consistency condition (6.8.7). Then the multistep
method (6.8.1) is stable if and only if the root condition (6.8.9),
(6.8.10) is satisfied.
Proof
l.
We begin by showing the necessity
of
the root condition for stabil-
ity.
To
do so, assume the opposite by letting
llj(O)
I > 1
for some
j.
Consider the differential equation problem
y'
=
0,
y(O) =
0,
with the solution
Y(x)
= 0. Then (6.8.1) becomes
p
Yn+l
= L
ajYn-j
j-0
n;<::p
{6.8.23)
If
we take
Yo
= y
1
= · · · =
Yp
=
0,
then the numerical solution
is
clearly

CONVERGENCE AND STABILITY THEORY
FOR
MULTISTEP METHODS
399
y,
=
0,
with all n
2:::
0.
For
the perturbed initial values, take
(6.8.24)
For
these initial values,
which is a uniform bound for
all small values
of
h, since the right side is
independent
of
h.
As
£
-+
0, the bound also tends to zero.
The solution
of
(6.8.24) with the initial conditions (6.8.24)
is
simply
For
the deviation from {y,},
I
'
N(h)
Max
IY,-
z,l
= £
ij(O)
·
Xo:SXnSb
. ·
As
h-+
0,
N(h)-+
co
and the bound becomes infinite. This proves the
method. is unstable when some
lij(O)I >
1.
If
the root condition is
violated instead
by
assuming (6.8.10) is false, then a similar proof can be
given. This is left
as
Problem 29.
2.
Assume the root condition
is
satisfied.
The
proof
of
stability will be
restricted to the model equation
(6.8.13). A proof can be given for the
general equation
y'
=
f(x,
y),
but
it
is a fairly involved modification
of
the following proof. The general proof involves the solution
of
nonhomo-
geneous linear difference equations [see Isaacson and Keller
(1966), pp.
405-417, for a complete development]. To further simplify the proof,
we
assume that the roots
!j(O),
j =
0,
1,
...
, p are all distinct.
The
same will
be true of
!j(h'A), provided the value
of
h is kept sufficiently small, say
0
~
h
~
h
0
•
Let { y,} and { z,}
be
two solutions
of
(6.8.19) on
[x
0
,
b
J,
and assume
Max
IY,-
z,l
~
£
Osnsp
0 < h
~
h
0
( 6.8.25)
Introduce the error e, =
y,
-
z,.
Subtracting using (6.8.19) for each
solution,
p
(1
-
hAb_
1
)e,+
1
- L (
aj
+
h'Ab)en-j
= 0
j-0
for
xp+l
~
xn+l
~b.
The general solution is
p
e, =
L:
rA!j(h'A)]"
n:<::O
j-0
(6.8.26)
( 6.8.27)

'
i
I
J
400 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS
The coefficients y
0
(h),
...
, Yp(h) must
be
chosen so
that
The
solution (6.8.27) will then agree with the given initial perturbations
e
0
,
...
,
eP,
and it will satisfy the difference equation (6.8.26). Using the
bound
(6.8.25) and the theory
of
systems
of
linear equations,
it
is fairly
straightforward to show
that
Max
lr;l
::;;
c
1
t:
O:s;i:Sp
0 < h::;; h
0
(6.8.28)
for some constant c
1
> 0. We omit the
proof
of
this, although it can be
carried out easily by using concepts introduced in Chapters 7 and 8.
To
bound the solution
en
on
[x
0
,
b], we must bound each term
[lj(hAW.
To do so, consider the expansion
'j(u)
= lj(O) +
urj(r)
(6.8.29)
for some f between 0
and
u.
To
compute
rj(u),
differentiate the
characteristic equation
Then
(6.8.30)
By
the
assumption that lj(O) is a simple
root
of
p (
r)
= 0, 0
::;;
j
::;;
p,
it
follows that p'(!j(O))
=F
0,
and
by continuity,
p'(lj(u))
=F
0 for all suffi-
ciently small values
of
u.
The
denominator
in
(6.8.30)
is
nonzero,
and
we
can
bound
rj(u)
all
lui
::;;
u
0
for some u
0
> 0.
Using this with (6.8.29)
and
the root condition (6.8.9}, we have
llj(h;\)
I::;;
10(0)
I+
c
2
lhAI
::;;
1 + c
2
jh;\l
lfrAh;\)]
nl::;;
[1 +
c21hAir::;;
ec2nih>-i::;;
ec2(b-xo>i>..i
(6.8.31)
