Atkinson K. An Introduction to Numerical Analysis
Подождите немного. Документ загружается.


(b)
y"
-
.1(1
- y
2
)y'
+ y = 0, y(O) =
1,
y'(O) = 0
(Van der Pol's equation)
(c)
x"(t)
=
-xjr
3
,
y"(t)
=
-yjr
3
,
r =
/x
2
+ y
2
(orbital equation)
x(O) = .4, x'(O) =
0,
y(O) = 0, y'(O) = 2
PROBLEMS
451
4. Let
Y(x)
be
the solution, if it exists, to the initial value problem (6.0.1).
By
integrating, show that Y satisfies
Y(x)
= Y
0
+
jxf(t,
Y(t))
dt
xo
Conversely, show that if this equation has a continuous solution
on
the
interval
x
0
::5:
x
::5:
b,
then the initial value problem (6.0.1) has the same
solution.
5.
The
integral equation
of
Problem 4 is solved,
atleast
in theory,
by
using the
iteration
6.
Ym+l(x) =
Yo+
jxf(t,
Ym(t))
dt,
xo
Xo
::5:
X
::5:
b
for
m;;:::;
0, with Y
0
(x)
= Y
0
•
This is called Picard iteration, and under
suitable assumptions, the iterates {
Ym(x)}
can
be shown to converge
uniformly to
Y(x).
Illustrate this by computing the Picard iterates Y
1
,
Y
2
,
and
Yj for the following problems; compare them to the true solution
Y.
(a)
y'
=
-y,
y(O) = 1
(b)
y'
=
-xy,
y(1) = 2
(c)
y'
= y +
2cos(x),
y(O) = 1
Write a computer program to solve
y'
=
f(x,
y),
y(x
0
)
= y
0
,
using Euler's
method. Write it to be used with
an
arbitrary f, stepsize
h,
and
interval
[x
0
,b]. Using the program, solve
y'
= x
2
-
y,
y(O) = 1, for 0
::5:
x
::5:
4,
with stepsizes of
h = .25, .125, .0625,
in
succession.
For
each value
of
h,
print
the true solution, approximate solution, error,
and
relative error
at
the
nodes
x = 0, .25, .50, .75,
...
, 4.00. The true solution is
Y(x)
= x
2
-
2x
+
2 -
e-x.
Analyze your
output
a:nd
supply written comments on it. Analysis
of
output
is as important as obtaining it.
7.
For
the problem
y'
=
y,
y(O) =
1,
give the explicit solution {
Yn}
for
Euler's approximation to the equation.
Use
this
to
show that for
xn
= 1,
Y(1) -
Yn
=
(h/2)e
ash~
0.

452
NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS
8. Consider solving the problem
x~O
y(O)
= 1
by Euler's method. Compare (1) the bound (6.2.13), using K = 2
as
the
Lipschitz constant, and (2) the asymptotic estimate from (6.2.36). The true
solution is
Y(x)
=
1/(1
+
x).
9.
Show that Euler's method fails to approximate the solution Y(x) =
(fx)
3
1
2
,
x
~
0,
of
the problem
y'
= y
1
1
3
,
y(O)
= 0. Explain why.
10.
For
the equations in Problem
3,
write
out
the approximating difference
equations obtained by using Euler's
metho~.
11.
Recall the rounding error example for Euler's method, with the results
shown in Table
6.3.
Attempt to produce a similar behavior on your
computer by letting
h become smaller, until eventually the error begins to
increase.
12. Convert the problem
yO>+
4y"
+
5y'
+
2y
=
-4sin(x)-
2cos(x)
y(O)
= 1
y'(O)
= 0
y"(O) =
-1
to a system
of
first-order equations. Using Euler's method, solve this system
and empirically study the error. The true solution
is
Y(x)
=
cos(x).
13.
(a) Derive the Lipschitz condition (6.2.52) for a system
of
two differential
(b)
equations.
~,
Prove that the method (6.2.51) will converge to the solution of
(6:2.50).
14. Consider the two-step method
15.
16.
withy~
=
f(x,.,
y,.). Show it
is
a second-order method, and find the leading
term
in
the truncation error, written as in (6.3.15).
Assume
that
the multistep method (6.3.1) is consistent and that it satisfies
ai
~
0, j = 0,
1,
...
, p, the same as
in
Theorem
6.6.
Prove stability of
(6.3.1), in analogy with (6.2.28), for Euler's method, but letting
8 =
0.
Write a program to solve
y'
=
f(x,
y),
y(x
0
)
= y
0
,
using the midpoint rule
(6.4.2).
Use a
fixed
stepsize
h.
For the initial value Jr, use the Euler

PROBLEMS
453
method:
Y1
=Yo+
hf(xo,
Yo)
With the program,
solve
the following problems:
(a)
y'
=
-y
2
,
y(O)
= 1;
Y(x)
=
lj(1
+
x)
y [ y ]
20
(b)
y'
= 4 1 -
20
, y(O) = 1;
Y(x)
=
[1
+
19e-xl4]
(c)
y'
=
-y
+
2cos(x),
y(O) =
1;
Y(x)
=
cos(x)
+
sin(x)
(d)
y'
=
y-
2sin(x),
y(O) =
1;
Y(x)
=
cos(x)
+
sin(x)
Solve
on
the interval [x
0
,
b]
=
[0,
5],
with h =
.5,
.25.
Print the numerical
solution
Yn
= yh(xn) at each node, along with the true error. Discuss your
results.
17.
Write a program
to
solve
y'
=
f(x,
y),
y(x
0
)
= y
0
,
using the trapezoidal
rule (6.5.2) with a
fixed
stepsize h. In the iteration (6.5.3), use the midpoint
method
as
the predictor of
y~2
1
•
Allow the number of iterates J to be an
input variable,
J
~
1.
Solve the equations in Problem
16
with h =
.5
and
.25,
for [x
0
,
b]
=
(0,
10].
Solve over the entire interval with J = 1, then
repeat the process with
J =
2;
and then J =
3.
Discuss the results. How
does the total error vary with
J?
18.
Derive the asymptotic error formula (6.5.19) for the trapezoidal method.
19.
Write a program to implement the algorithm Detrap of Section
6.6.
Using
it, solve the equations given in Problem 16, with
t:
= .001.
20.
Use the quadratic interpolant to
Y'(x)
=
f(x,
Y(x))
at xn,
xn_
1
, xn_
2
to
obtain the formula
When the truncation error
is
dropped, we obtain the method
4h
Yn+1
= Yn-3 +
3[2y~-
Y~-1
+
2y~-2]
n~3
This is the predictor formula for the Milne method (6.7.13).
21.
Show that the Simpson method (6.7.13) is only weakly stable, in the same
sense as was true of the midpoint method in Section 6.4.

i
i
__j
!
454
NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS
22. Write a program
to
solve
y'
=
f(x,
y),
y(x
0
)
= y
0
,
x
0
~
x
~
b,
using the
fourth-order Adams-Moulton formula and a
fixed
stepsize h. Use the
fourth-order Adams-Bashforth formula
as
the predictor. Generate
the initial values
y
1
,
h•
y
3
using true solution
Y(x).
Solve
the equations
of
Problem
16
with h =
.5
and h =
.25.
Print the calculated answers and the
true errors. For comparison with method (6.7.27), also solve the example
used in Table
6.14.
Check the accuracy of the Richardson extrapolation
error estimate
that is based on the global error being of the fourth order. Discuss all your
results.
23. (a)
For
the coefficients
Y;
and
8;
of the Adams-Bashforth and
Adams-Moulton
formula&,
show that
8;
=
Y;-
Y;-
1
,
i
:2::
1.
(b)
For
the p-step Adams-Moulton formula (6.7.26), prove
-
(0)
+ h
:vp+l
'
Yn+I-
Yn+I
Yp
Yn+I
(1)
with
y~~\
the p + 1 step Adams-Bashforth formula from (6.7.22),
p
Y
(O)
= y + h
""
y'!\Jly. '
n+l
n
~
J n
(2)
j=O
These formulas are both of order p + 1. The result (1)
is
of use in
calculating the corrector from the predictor, and
is
based on carrying
certain backward differences from one step to the next. There is a
closely related result when a p-step predictor (order
p)
is
used to
solve the p-step corrector (order
p + 1)
[see
Shampine and Gordon
(1975), p.
51].
24.
Consider the model equation (6.8.16) with A a square matrix of order m.
Assume A =
p-
1
DP, with D a diagonal matrix with entries i\
1
,
.••
, i\m.
Introduce the new unknown vector function z =
p-
1
y(x). Show that
(6.8.16) converts to the form given in (6.8.17), demonstrating the reduction
to the one-dimensional model equation.
25. Following the ideas given in
Sections 6.4 and
6.8,
give the general proce-
dure for solving the linear difference equation
Apply this to
find
the general solution of the following equations.
(a) Yn+I = -
fYn
+ tYn-1
(b)
Yn+
1
=
Yn-
i.Yn-
1
Hint: See the formula following (6.8.22).

PROBLEMS 455
26.
Solve the third-order linear difference equation
n:::?:2
O<c<l
with u
0
,
u
1
, u
2
given. What can be said about
Limitun
n-+
oo
27. Consider the numerical method
Determine its order. Illustrate with an example that the method
is
unstable.
28. Show that the two-step method
is
of order 2 and unstable. Also, show directly that it need not converge
when solving
y'
=
f(x,
y).
29. Complete part
(1)
of the proof of Theorem 6.7, in which the root condition
is violated by assuming
lrjl
=
1,
p'(r)
=
0,
for some
j.
30.
For
part
(2) of the proof of Theorem 6.8, show· that
-y)r/hAW
~
0 as
h
~
0, 1
5,
j
5,
p.
31. (a) Determine the values
of
a
0
in the explicit second-order method
(6.7.10) for which the method is stable.
(b)
If
only the truncation error (6.7.11)
is
considered, subject to the
stability restriction in part (a), how should
a
0
be chosen?
(c)
To
ensure a large region of stability, subject to part (a), how should a
0
be chosen?
32. (a) Find the general formula for all two-step third-order methods. These
will be a one-parameter family
of
methods, say, depending on the
coefficient
a
1
•
(b) What are the restrictions on a
1
for the method in part (a) to be
stable?
(c)
If
the truncation error
is
writ'ten as
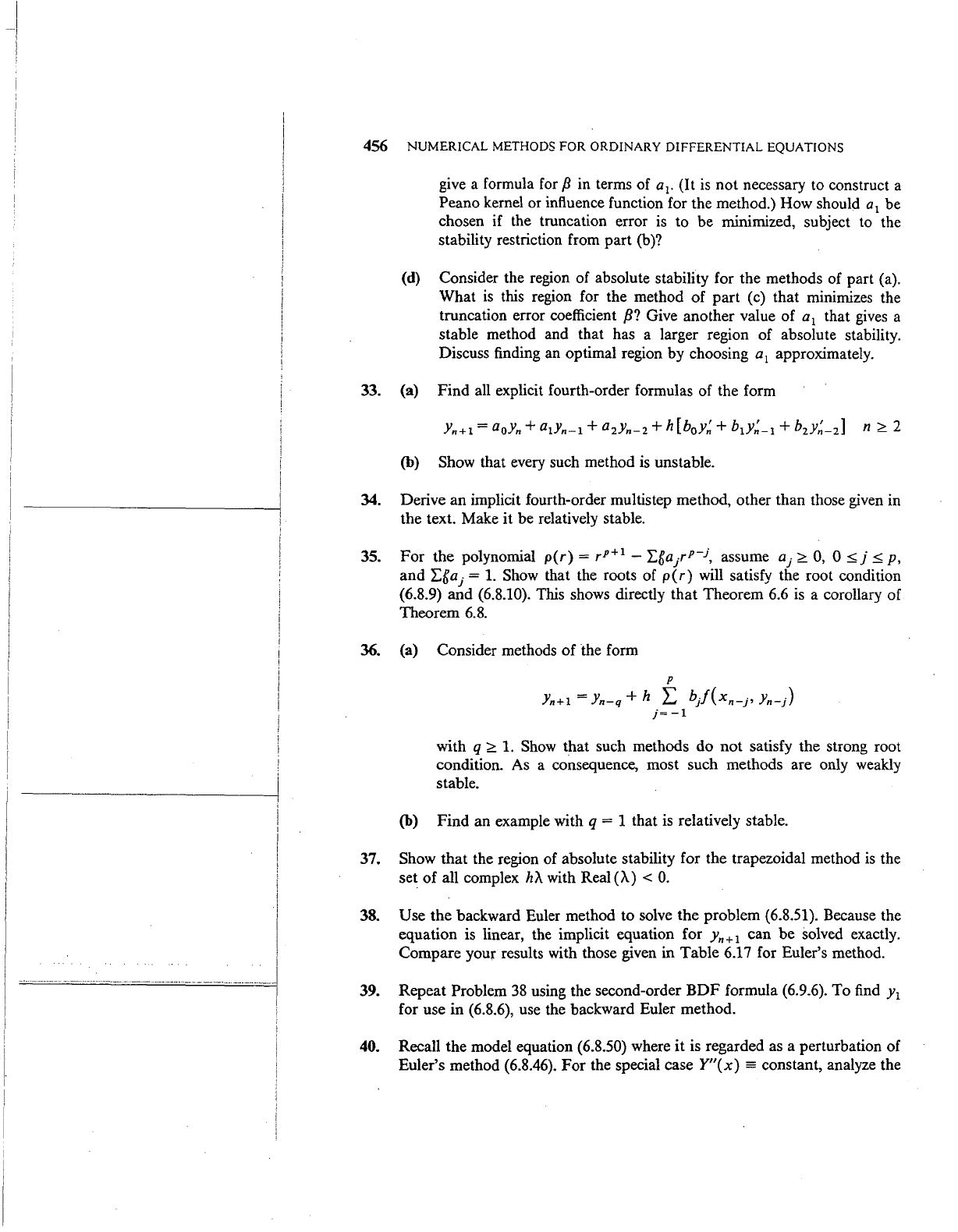
I
I
J
456
NUMERICAL
METHODS FOR ORDINARY
DIFFERENTIAL
EQUATIONS
give
a formula
for
fJ
in terms of a
1
.
(It
is
not necessary to construct a
Peano kernel or influence function for the method.) How should a
1
be
chosen if the truncation error
is
to be minimized, subject to the
stability restriction from part (b)?
(d) Consider the region of absolute stability for the methods of part (a).
What
is
this region for the method of part
(c)
that minimizes the
truncation error coefficient
fJ?
Give another value of a
1
that
gives
a
stable method and that has a larger region of absolute stability.
Discuss finding an optimal region by choosing
a
1
approximately.
33. (a) Find all explicit fourth-order formulas of the form
(b) Show that every such method
is
unstable.
34. Derive
an
implicit fourth-order multistep method, other than those given in
the text. Make it be relatively stable.
35. For the polynomial
p(r)
=
rP+l-
L.gajrp-j'
assume
aj
~
0,
0
5;j
5:,
p,
and L.gaj =
1.
Show
that the roots of
p(r)
will satisfy the root condition
(6.8.9) and (6.8.10). This shows directly that Theorem 6.6
is
a corollary of
Theorem
6.8.
36. (a) Consider methods
of
the form
p
Yn+l
= Yn-q + h L
bJ(xn-j•
Yn-j)
j=
-1
with q
~
1.
Show
that such methods do not satisfy the strong root
condition.
As
a consequence, most such methods are only weakly
stable.
(b) Find an example with q = 1 that
is
relatively stable.
37. Show that the region of absolute stability for the trapezoidal method
is
the
set of all complex
hA
with Real (X) <
0.
38. Use the backward Euler method to solve the problem (6.8.51). Because the
equation is linear, the implicit equation for
Yn+l can be solved exactly.
Compare your results with those given in Table
6.17 for Euler's method.
39. Repeat Problem
38 using the second-order
BDF
formula (6.9.6). To
find
y
1
for use in (6.8.6), use the backward Euler method.
40. Recall the model equation (6.8.50) where it is regarded as a perturbation of
Euler's method
(6.8.46). For the special case
Y"(x)
=constant,
analyze the

PROBLEMS 457
behavior
of
the error Y(xn) -
Yn
as it depends on
hA..
Show that again the
condition (6.8.49) is needed in order
that
the error
be
well-behaved.
41. Derive the truncation error formula (6.9.7) for backward differentiation
formulas.
42.
For
solving
y'
=
f(x,
y), consider the numerical method
h h
2
Yn+l
=
Yn
+
l[y~
+
Y~+l]
+
12
[y~'-
Y~
1
+1]
n
~
0
y~'
=
with this formula based
on
differentiating
Y'(x)
=
f(x,
Y(x)).
(a) Show that this is a fourth-order method:
T,(Y)
= O(h
5
).
(b) Show that the region
of
absolute stability contains the entire negative
real axis
of
the complex hA.-plane.
43. Generalize the method
of
lines, given
in
(6.9.23)-(6.9.25), to the problem
llr
=
a(x,
t)Uxx +
G(x,
t,
U(x,
t))
O<x<l
t > 0
U(O,
t)
= d
0
(t) t
~
0
U(x,O)
=f(x)
For
it
to be well-defined, we assume
a(x,
t)
> 0, 0
~
x
~
1, t
~
0.
44. (a)
If
you have a solver
of
tridiagonal linear algebraic systems available to
you, then write a program to implement the method
of
lines for the
problem (6.9.19)-(6.9.21). The example in the text, with the unknown
(6.9.35), was solved using the backward Euler method. Now imple-
ment the method
of
lines using the trapezoidal rule. Compare your
results with those
in
Table 6.20 for the backward Euler method.
(b) Repeat with the second-order
BDF
method.
45. Derive a third-order Taylor series method to solve
y'
= - y
2
•
Compare the
i numerical results to those in Table 6.22 .
..
.i
46. Using the Taylor series method of Section 6.10, produce a fourth-order
method to solve
y'
=
x-
y
2
,
y(O) =
0.
Use fixed stepsizes, h = .5, .25,
.125
in
succession, and solve for 0
~
x
~
10. Estimate the global error
using the error estimate (6.10.24) based on Richardson extrapolation.

:
i
I
~
I
j
I
I-
I
J
458 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS
47. Write a program to solve
y'
=
f(x,
y),
y(x
0
)
= y
0
,
using the classical
Runge-Kutta method
(6.10.21), and let the stepsize h be fixed.
(a)
Using the program, solve the equations of Problem 16.
(b) Solve
y'
= x - y
2
,
y(O) =
0,
for h = .5, .25, .125. Compare the
results with those of Problem
46.
48. Consider the three stage
Runge-
Kutta formula
Determine the set
of
equations that the coefficients {
"Yj•
aj,
f3j;}
must satisfy
if the formula
is
to be of order
3.
Find a particular solution of these
equations.
49. Prove that if the Runge-Kutta method (6.10.4) satisfies (6.10.27), then it
is
stable.
50. Apply the classical Runge-Kutta method (6.10.21) to the test problem
(6.8.51), for various values of
A.
and
h.
For example, try
A.
=
-1,
-10,
-50
and h = .5, .1, .01, as in Table 6.17.
51. Calculate the real part of the region of absolute stability for the
Runge-Kutta
method of (a) (6.10.8), (b) (6.10.9), (c) (6.10.21).
We
are
interested in the behavior of the numerical solution for the differential
equation
y'
=
A.y
with
Real(:\)<
0.
In particular,
we
are interested in
those values of
hA.
for which the numerical solution tends to zero as
Xn
~
00.
52. (a) Using the Runge-Kutta method (6.10.8), solve
(b)
y'
=
-y
+ x·
1
[1.1 + x]
y(O)
= 0
whose solution is
Y(x)
=xu.
Solve the equation on
[0,
5],
pri~ting
the errors at x = 1,
2,
3,
4,
5.
Use stepsizes h =
.1,
.05, .025, .0125,
.00625. Calculate the errors by which the errors decrease when h is
halved. How does this compare with the usual theoretical rate
of
convergence of
0(
h
2
)?
Explain your results.
What difficuhy arises when trying to use a Taylor
wethod of order
~
2 to solve the equation of part (a)? What does it tell us about the
solution?

I
=···-=···-=--=····=·
=··=·····=--=--=-
=·-··=····=··==·--=-=···=·····=·--=-··"-'·-
·=--=···=··-=··
=··--.~
.,
PROBLEMS 459
53. Convert the boundary value problem (6.11.1) to an equivalent boundary
value problem for a system of first-order equatiens, as in (6.11.15).
54. (a) Consider the two-point boundary value problem (6.11.25). To convert
this to an equivalent problem with zero boundary conditions, write
y(x)
=
z(x)
+
w(x),
with
w(x)
a straight line satisfying the follow-
ing boundary conditions:
w(a)
= y
1
,
w(b)
= y
2
•
Derive a new
boundary value problem for
z( x ).
(b) Generalize this procedure to problem (6.11.10). Obtain a
new
problem
with zero boundary conditions: What assumptions, if any, are needed
for the coefficients
a
0
,
a
1
,
b
0
,
b
1
?
55. Using the shooting method of Section 6.11, solve the following boundary
value problems. Study the convergence rate as
h is varied.
-2
1 2
(a)
y"
=
--;-yy',
1 < x <
2;
y(1)
= 2'
y(2)
= 3
True solution:
Y(x)
=
xj(1
+
x).
(b)
y"
=
2yy',
0
<X<
-i;
y(O) = 0,
y(
-i)
= 1
True solution:
Y(x)
=
tan(x).
56. Investigate the differential equation programs provided by your computer
center. Note those that automatically control the truncation error by
varying the stepsize, and possibly the order. Classify the programs as
multistep (fixed-order or variable-order), Runge-Kutta, or extrapolation.
Compare one of these with the programs DDEABM [of Section
6.7
and
Shampine and Gordon
(1975)]
and RKF45 [of Section 6.9 and
Shampine and Watts (1976b)] by solving the problem
y'
=
~[1-
~]
4
20
y(O) = 1
with desired absolute errors of 10-3,
10-
6
,
and
10-
9
•
Compare the results
with those given in Tables
6.15
and 6.28.
57. Consider the problem
1 1
y'
=
--
+ c ·
tan-
1
(y(t))-
-
t+1
2
y(O) = 0
with c a given constant. Since y'(O) =
},
the solution
y(t)
is initially
increasing as
t increases, regardless of the value
of
c.
As best you can, show
that there
is
a value of
c,
call it
c*,
for which (1) if c >
c*,
the solution
y(t)

~I
460 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS
increases indefinitely, and
(2)
if c < c*, then
y(
t)
increases initially, but
then peaks and decreases. Determine
c* to within .00005, and then calcu-
late the associated solution
y(
t)
for 0
~
t
~
50.
58. Consider the system
x'(t)
=Ax~
Bxy
y'(t)
=
Cxy-
Dy
This
is
known as the Lotka-Volterra predator-prey model for two popula-
tions, with
x(t)
being the number of prey and
y(t)
the number of
predators,
at
time t.
(a) Let A =
4,
B =
2,
C = 1, D =
3,
and
solve the model to at least
three significant digits for
0
~
t
~
5.
The initial values are
x(O)
=
3,
y(O)
=
5.
Plot x and y as functions of t, and plot x versus y.
(b) Solve the same model with
x(O)
= 3 and, in succession,
y(O)
=
1,
1.5,
2.
Plot x versus y in each case. What
do
you observe? Why would the
point
(3,
2)
be called an equilibrium point?
