Atkinson K. An Introduction to Numerical Analysis
Подождите немного. Документ загружается.


BOUNDARY
VALUE
PROBLEMS 441
Finite difference methods
We
consider the two-point
BVP
y"
=
f(x,
y,
y')
a<x<b
y(a)=yl
y(b)=y2
(6.11.25)
with the true solution denoted by
Y(x).
Let n >
1,
h =
(b-
a)jn,
xj
=a+
jh
for j =
0,
1,
...
, n. At each interior node point
X;,
0 < i < n, approximate
Y"(x;)
and Y'(x;):
{6.11.26)
for some
X;_
1
.s;
E;,
1J;
.s;
xi+l• i =
1,
...
, n - 1. Dropping the
final
error terms
and using these approximations in the differential equation,
we
have the ap-
proximating nonlinear system:
i = 1,
...
,
n-
1 (6.11.27)
This
is
a system
of
n-
1 nonlinear equations in
then
- 1 unknowns y
1
,
•••
, Yn-l·
The values y
0
= y
1
and
Yn
= y
2
are known from the boundary conditions.
The analysis of the error in {
Y;}
compared to {
Y(
x;)}
is
too complicated to be
given here,
as
it requires the methods of analyzing the solvability of systems
of
nonlinear equations. In essence, if
Y(x)
is
four times differentiable, if the
problem (6.11.25) is uniquely solvable for some region about the graph on
[a, b]
of
Y(x
), and if
f(x,
u,
v)
is
sufficiently differentiable, then there
is
a solution to
(6.11.27) and it satisfies
(6.11.28)
For an analysis, see Keller
(1976,
Sec.
3.2)
or Keller (1968,
Sec.
3.2). Moreover,
with additional assumptions on
f and the smoothness of
Y,
it can be shown that
{6.11.29)
with
T(x)
independent of h. This can be used to justify Richardson extrapola-
tion, to obtain results that converge more rapidly.
[Other methods to improve
convergence are based on correcting for the error in the central difference
approximations of (6.11.27).]
The system (6.11.27) can be solved in a variety of ways, some of which are
simple modifications of the methods described in Sections
2.10 and 2.11. In
!
\
.......
.!
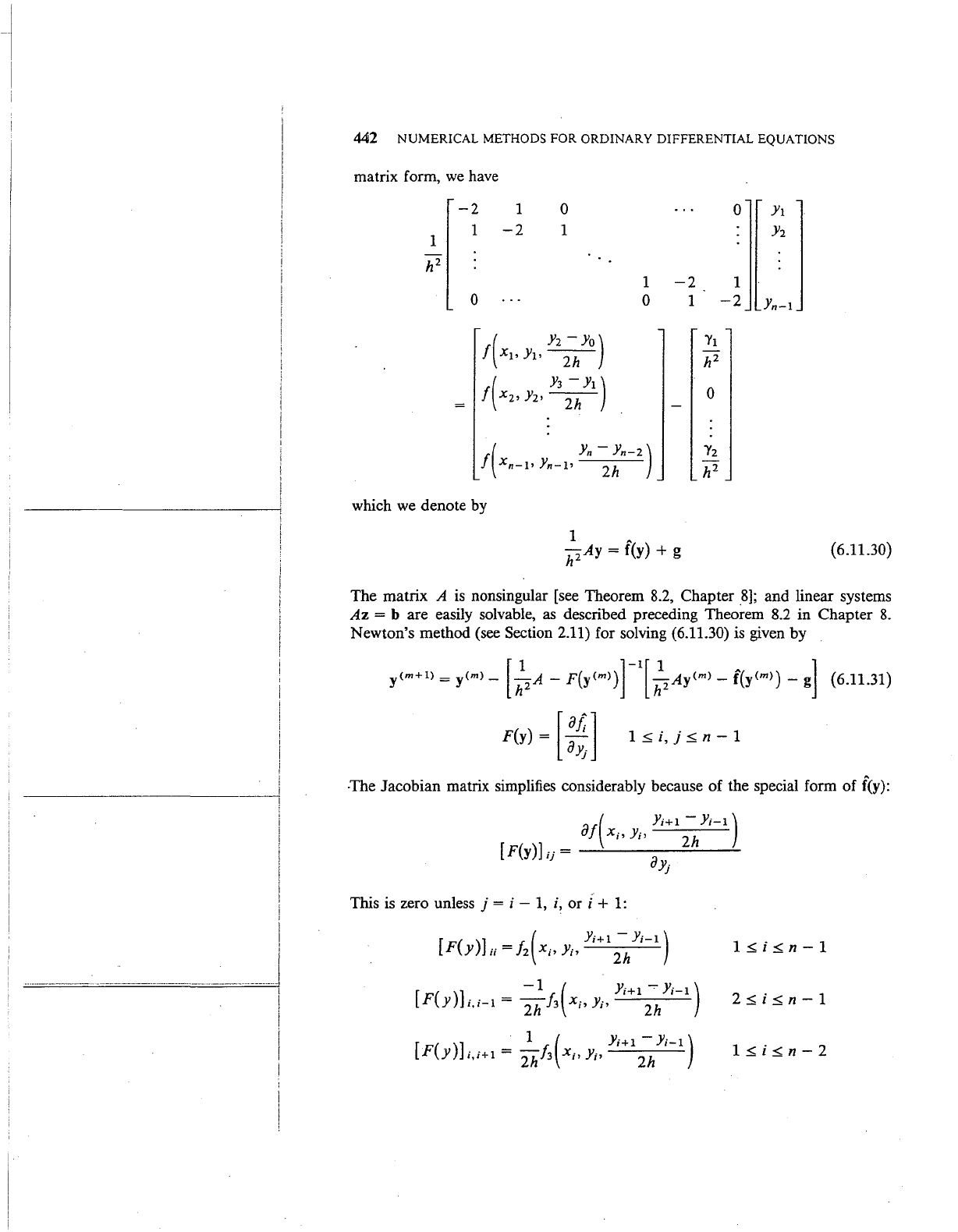
442 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS
matrix form,
we
have
-2
1
0
1
-2
0
1
(
Y2-
Yo)
I
X1,
Y1•
2h
(
Y3
- Y1)
f
X2,
Y2•
2
h
1
0
(
Yn-
Yn-2)
I xn-1• Yn-1• 2h
which
we
denote by
-2
1
1 A
h2Ay = f(y) + g
0
Y1
Y2
1
-2
Yn-1
'Y1
h2
0
(6.11.30)
The matrix A
is
nonsingular [see Theorem
8.2,
Chapter
8];
and linear systems
Az
= b are easily solvable,
as
described preceding Theorem
8.2
in Chapter
8.
Newton's method (see Section 2.11) for solving (6.11.30) is given by
(6.11.31)
1
:::;;
i,
j:::;; n - 1
The
Jacobian matrix simplifies considerably because of the special form of f(y):
at(
. .
Yi+1
- Y1-1)
x,
y,, 2h
[F(y)]
ij
= a
Yj
This
is
zero unless j =
i-
1,
i, or i +
1:
[ (
)]
(
Yi+1-Yi-1)
F y
ii
=
/2
X;,
Y;,
2h
-1
(
Y1+1...,.
Y;-1)
[F(y
)L,i-1 = 2h
/3
X;,
Y;,
2h
· 1 (
Yi+1-Yi-1)
[F(y
)L./+1 = 2h/3
X;,
Y;,
2h

-·.
·---····-·-·-
-·-
----
------
. --··--·-- - --- -----·····--- ---····-
--:
BOUNDARY VALUE PROBLEMS
443
with f
2
(x,
u, u) and f
3
(x,
u,
v) denoting partial derivatives with respect to u and
v, respectively. Thus the matrix being inverted in (6.11.31)
is
of the special form
we call
tridiagonal. Letting
(6.11.32)
we can rewrite (6.11.31) as
y(m+l)
=
y(m)
_
8(m)
(6.11.33)
This linear system is easily and rapidly solvable, as shown in Section 8.2
of
Chapter
8.
The
number
of
multiplications and divisions can be shown to about
5n, a relatively small number of operations for solving a linear system of n - 1
equations. Additional savings can be made by
not
varying
B,
or by only
changing
it
after several iterations
of
(6.11.33).
For
an extensive survey and
discussion
of
the solution of nonlinear systems that arise in connection with
solving
BVPs, see Deuflhard (1979).
Example
We applied the preceding finite difference procedure (6.11.27) to the
solution
of
the BVP (6.11.22), used earlier to illustrate the shooting method. The
results are given in Table
6.30 for successive doublings of n =
2jh.
The nonlin-
ear
system in (6.11.27) was solved using Newton's method,
as
described in
(6.11.33).
The
initial guess was
y~O>(x;)
=
(e
+
e-1)-1
i =
0,
1,
...
, n
based
on
connecting the boundary values
by
a straight line. The quantity
dh
=
M~
IY/m+l)-
y/m)l
o:s;,:s;n
was computed for each iterate, and when the condition
Table
6.30 The finite difference method
for solving (6.11.22)
2
n=-
Eh
Ratio
h
4
.2.63E-
2
8
·s.87E-
3
4.48
16
1.43E-
3 4.11
32
3.55E-
4
4.03
64
8.86E-
5
4.01

444 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS
was satisfied, the iteration
was
terminated. In all cases, the number of iterates
computed was 5 or
6.
For the error, let
with
Yh
the solution of (6.11.27) obtained with Newton's method. According to
(6.11.28) and (6.11.29),
we
should expect the values
Eh
to decrease by about a
factor of 4 when
h
is
halved, and that
is
what
we
observe in the table.
Higher order methods can be obtained in several ways. (1)
Use higher order
approximations to the derivatives, improving (6.11.26); (2) use Richardson ex-
trapolation, based on (6.11.29); as with Romberg integration,
it
can be repeated
to obtain methods of arbitrarily high order; (3) the truncation errors in (6.11.26)
can be approximated with higher order differences using the calculated values of
Yh·
Using these values as corrections to (6.11.27),
we
can obtain a new more
accurate approximation to the differential equation
in
(6.11.25), leading to a more
accurate solution.
All
of these techniques have been used, and some have been
implemented as quite sophisticated computer codes. For a further discussion and
for examples of computer codes, see Fox
(1980, p. 191), Jain (1984, Chap.
4),
and
Pereyra (1979).
Other methods and problems There are a number of other methods used for
solving boundary value problems. The most important of these
is
probably the
collocation method. For discussions referring to collocation methods, see Reddien
(1979), Deuflhard
(1979),
and Ascher and Russell (1985). For an important
collocation computer code, see Ascher et al. (1981a) and (1981b).
Another approach to solving a boundary value problem
is
to solve an
equivalent reformulation as an integral equation. There
is
much less development
of such numerical methods, although they can be very effective in some situa-
tions. For an introduction to this approach, see Keller (1968, Chap. 4).
There are also many other types of boundary value problems,
some containing
some type of these singular behavior, that
we
have not discussed here. For
all
of
these, see the papers in the proceedings of Ascher and Russell (1985), Aziz
(1975), Childs et
al.
(1979), and Gladwell- and Sayers (1980); also see Keller
(1976, Chap. 4) for singular problems. For discussions of software, see Childs
et
al.
(1979), Gladwell and Sayers (1980), and Enright (1985).
Discussion
of
the Literature
Ordinary and partial differential equations are the principal form of mathemati-
cal model occurring in the sciences and engineering,
and
consequently, the
·numerical solution of differential equations
is
a very large area of study. Two
classical
books that reflect the state of knowledge before the widespread use of
digital computers are Collatz (1966) and Milne (1953). Some important and

\
·-··-·- -------- ---------
----
___________
..
___________________________________
,
________
-
-\
DISCUSSION
OF
THE
LITERATURE
445
general books, since 1960,
in
the numerical solution of ordinary differential
equations are Henrici (1962), Gear
(1971),
Lapidus and Seinfeld (1971), Lambert
(1973),
Stetter (1973), Hall and Watt (1976), Shampine and Gordon (1975),
Vander
Houwen (1977), Ortega and Poole (1981), and Butcher (1987). A useful
survey is given in Gupta et
al.
(1985).
The modern theory of convergence and stability of multistep methods, intro-
duced
in
Section 6.8, dates from Dahlquist (1956). An historical account
is
given
in Dahlquist (1985). The text by Henrici (1962) has become a classic account of
that theory, including extensions and applications of it. Gear (1971) is a more
modern account of all methods, especially variable order methods.
Stetter (1973)
gives a very general and complete abstract analysis of the numerical theory for
. solving initial value problems. A complete account up to
1970 of
Runge-Kutta
methods, their development and error analysis,
is
given in Lapidus and Seinfeld
(1971). Hall and Watt (1976)
gives
a survey of all aspects of the solution of
ordinary differential equations, including the many special topics that have
become of greater interest in the past ten years.
The first significant use of the concept of a variable order method is due to
Gear (1971) and Krogh (1969).
Such methods are superior to a fixed-order
multistep method in efficiency, and they do not require any additional method
for starting the integration or for changing the stepsize. A very good account of
the variable-order Adams method
is
given
in
Shampine and Gordon (1975)
and the excellent code
DE/STEP
is
included. Other important early codes based
on the Adams family of formulas
were
those in Krogh (1969), DIFSUB from
Gear (1971), and GEAR from Hindmarsh (1974). The latter program
GEAR
has
been further developed into a large multifunction package, called ODEPACK,
and it
is
described
in
Hindmarsh (1983). Variants of these codes and other
differential equation solvers are available in the
IMSL and NAG libraries.
Runge-Kutta
methods are a continuing active area of theoretical research and
program development, and a very general development
is
given in Butcher (1987).
New methods are being developed for nonstiff problems; for example, see
Shampine (1986) and Shampine and Baca (1986). There
is
also great interest in
implicit
Runge-Kutta
methods, for
use
in solving stiff differential equations.
For
a survey of the latter, see Aiken
(1985,
pp. 70-92). An important competitor to
the code RKF45
is
the code DVERK described in Hull et al. (1976).
It
is
based
on a Fehlberg-type scheme, with a pair of formulas of orders
5 and
6.
A third class of methods has been ignored in our presentation, those based on
extrapolation.
Current work in this area began with Gragg (1965) and Bulirsch
and
Stoer (1966). The main idea
is
to perform repeated extrapolation on some
simple method, to obtain methods of increasingly higher order. In effect, this
gives another way to produce variable-order methods. These methods have
performed fairly
well
in the tests of Enright and Hull (1976) and Shampine et al.
(1976),
but
they were judged to not be as advanced in their practical and
theoretical development as are the multistep
and
Runge-Kutta methods.
For
a
recent survey of the area, see Deuflhard (1985). Also, see Shampine and Baca
(1986), in which extrapolation methods are discussed as one example of variable
order
Runge-Kutta
methods.
Global error estimation
is
an area in which comparatively little has been
published.
For
a general survey,
see
Skeel (1986). To our knowledge, the only

'
i
I
I
I
I
I
I
I
········-···-······----
··---1
446 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS
running computer code
is
GERK
from Shampine and Watts (1976a). Additional
work
is
needed
in
this area. Many users of automatic packages are under the
mistaken impression that the automatic codes they are using are controlling the
global error, but such global error control
is
not possible in a practical sense. In
many cases, it would seem to be important to have some idea of the actual
magnitude of the global error present in the numerical solution.
Boundary value problems for ordinary differential equations are another
important topic; but both their general theory and their numerical analysis are
much more sophisticated than for the initial value problem. Important texts are
Keller (1968) and (1976), and the proceedings
of
Child et
al.
(1979) gives many
important papers on producing computer codes. For additional papers, see the
collections of Aziz (1975), Hall and Watt (1976), and Ascher and Russell (1985).
This area
is
still comparatively young relative to the initial value problem for
nonstiff equations. The development of computer codes
is
proceeding in a
number of directions, and some quite good codes have been produced in recent
years. More work has been done on codes using the shooting method, but there
are also excellent codes being produced for collocation and finite difference
methods. For some discussion of such codes, see Enright (1985) and Gladwell
and
Sayers (1980, pp. 273-303). Some boundary value codes are given in the
IMSL and NAG libraries.
Stiff differential equations
is
one of several special areas that have become
much more important in the past ten years. The best general survey of this area
is
given in Aiken
(1985).
It
gives
examples of how such problems arise, the theory
of numerical methods for solving stiff problems, and a survey of computer codes
that exist for their solution. Many of the other texts in our bibliography also
address the problem of stiff differential equations. We also recommend the paper
of Shampine and Gear (1979).
Equations with a highly oscillatory solution occur in a number of applications.
For
some discussion of this, see Aiken (1985, pp. 111-123). The method of lines
for solving time-dependent partial differential equations is a classical procedure
that has become more popular in recent years.
It
is discussed in Aiken (1985, pp.
124-138), Sincovec and Madsen (1975), and Melgaard and Sincovec (1981).
Yet another area of interest
is
the solution of mixed systems of differential and
algebraic equations (DAEs). This refers to systems in which there are
n un-
knowns, m
< n differential equations, and n - m algebraic equations, involving
the
n unknown functions. Such problems occur in many areas of applications.
One such area of much interest in recent years
is
that of computer aided design
(CAD).
For
papers applicable to such problems and to other DAEs, see
Rheinboldt (1984) and (1986).
Because of the creation of a number of automatic programs for solving
differential equations, several empirical studies have been made to assess their
I
performance and to make comparisons between programs. Some of the major
comparisons are given in Enright and Hull (1976), Enright et
al.
(1975), and
Shampine et al. (1976).
It
is
clear from their work that programs must be
compared, as
well
as methods. Different program implementations of the same
method can vary widely in their performance.
No
similar results are known for
comparisons of boundary value codes.

i
- I
BIBLIOGRAPHY 447
Bibliography
Aiken, R., Ed. (1985).
Stiff
Computation. Oxford Univ. Press, Oxford, England.
Ascher,
U. (1986). Collocation for two-point
boundary
value problems revisited,
SIAM
J. Numer. Anal. 23, 596-609.
Ascher,
U.,
J.
Christiansen,
and
R. Russell (1981a). Collocation software for
boundary-value
ODEs,
ACM
Trans. Math. Softw. 7, 209-222.
Ascher,
U.,
J.
Christiansen,
and
R. Russell (1981b). COLSYS: collocation
software for boundary-value
ODEs,
ACM
Trans. Math. Softw. 7, 223-229.
Ascher,
U.,
and
R.
Russell, Eds. (1985). Numerical Boundary Value ODEs.
Birkhauser, Basel.
Aziz, A.
K., Ed. (1975). Numerical Solutions
of
Boundary
Value
Problems for
Ordinary Differential Equations.
Academic Press,
New
York.
Boyce, W.,
and
R. Diprima (1986). Elementary Differential Equations and
Boundary
Value Problems, 4th ed. Wiley,
New
York.
Bulirsch, R.,
and
J. Stoer (1966). Numerical
treatment
of
ordinary differential
equations
by
extrapolation, Numer. Math.
8,
1-13.
Butcher, J. (1965).
On
the attainable order
of
Runge-Kutta
methods, Math.
Comput.
19,
408-417.
Butcher, J. (1987). The Numerical Analysis
of
Ordinary Differential Equations.
Wiley,
New
York.
Childs, B., M. Scott,
J. Daniel, E. Denman,
and
P. Nelson, Eds. (1979). Codes for
Boundary-Value Problems
in
Ordinary Differential Equations. Lecture
Notes
in
Computer
Science 76, Springer-Verlag,
New
York.
Coddington,
E.,
and
N.
Levinson (1955). Theory
of
Ordinary Differential Equa-
tions.
McGraw-Hill, New York.
Collatz, L. (1966).
The Numerical Treatment
of
Differential Equations, 3rd ed.
Springer-Verlag, New York.
Dahlquist, G. (1956). Numerical integration
of
ordinary
differential equations,
Math. Scandinavica
4,
33-50.
Dahlquist, G. (1963). A special stability
property
for linear multistep methods,
BIT
3,
27-43.
.
Dahlquist, G. (1985).
33
years
of
numerical instability,
part
1,
BIT
25, 188-204.
Deuflhard, P. (1979). Nonlinear equation solvers
in
boundary
value problem
codes.
In
B.
Childs, M. Scott, J. Daniel,
E.
Denman,
and
P.
Nelson (Eds.),
Codes for Boundary-Value Problems
in
Ordinary Differential Equations,
pp.
40-66.
Lecture Notes_in Computer Science 76, Springer-Verlag, New York.
Deuflhard,
P. (1985). Recent progress in
extrapolation
methods for ordinary
differential equations,
SIAM
Rev. 27,
505-536.
Enright, W. (1985). Improving the performance
of
numerical methods for two-
point
boundary
value problems. In U.
Ascher
and
R. Russell (Eds.),
Numerical Boundary Value ODEs, pp.
107-120.
Birkhliuser, Basel.

I
;
I
I
I
__
I
448
NUMERICAL
METHODS FOR ORDINARY
DIFFERENTIAL
EQUATIONS
Enright,
W.,
and
T.
Hull
(1976).
Test results on initial value methods for non-stiff
ordinary differential equations,
SIAM
J. Numer. Anal.
13,
944-961.
Enright, W., T. Hull, and
B.
Lindberg (1975). Comparing numerical methods for
stiff systems of
O.D.E.'s,
BIT
15,
10-48.
Fehlberg,
E.
(1970). Klassische Runge-Kutta-Formeln vierter und niedrigerer
Ordnumg mit Schrittweiten-Kontrolle und ihre Anwendung auf Warme-
leitungsprobleme,
Computing
6,
61-71.
Forsythe, G.,
M.
Malcolm, and
C.
Moler (1977). Computer Methods for Mathe-
matical Computations. Prentice-Hall, Englewood Cliffs, N.J.
Fox,
L.
(1980). Numerical methods for boundary-value problems. In I. Gladwell
and D. Sayers (Eds.),
Computational Techniques for Ordinary Differential
Equations, pp. 175-217. Academic Press, New York.
Gear,
C.
W.
(1971). Numerical Initial Value Problems in Ordinary Differential
Equations. Prentice-Hall, Englewood Cliffs, N.J.
Gladwell,
1.,
and
D.
Sayers, Eds. (1980). Computational Techniques for Ordinary
Differential Equations. Academic Press, New York.
Gragg,
W.
(1965).
On
extrapolation algorithms for ordinary initial value prob-
lems,
SIAM
J.
Numer. Anal.
2,
384-403.
Gupta, G., R. Sacks-Davis, and
P.
Tischer (1985). A review of recent develop-
ments in solving
ODEs, Comput. Surv.
17,
5-47.
Hall, G., and J. Watt, Eds. (1976).
Modern Numerical Methods for Ordinary
Differential Equations. Oxford Univ. Press, Oxford, England.
Henrici,
P.
(1962). Discrete Variable Methods
in
Ordinary Differential Equations.
Wiley, New York.
Hindmarsh, A.
(1974).
GEAR: Ordinary differential equation solver. Lawrence
Livermore Rep.
UCID-30001,
Rev.
3,
Livermore, Calif.
Hindmarsh,
A. (1983). ODEPACK: A systematized collection
of
ODE
solvers. In
Numerical Methods for Scientific Computation, R. Stepleman, Ed. North-
Holland, Amsterdam.
Hull, T.,
W.
Enright, and
K.
Jackson (1976). User's guide for DVERK: A
subroutine for solving non-stiff
ODEs. Dept. Computer
Sci.
Tech. Rep. 100,
Univ.
of Toronto, Toronto, Ont., Canada.
Isaacson, E., and
H.
Keller (1966), Analysis
of
Numerical Methods. Wiley, New
York.
Jain, M.
K.
(1984). Numerical Solution
of
Differential Equations, 2nd ed. Halstead
Press, New York.
Keller, H. (1968). Numerical Methods for Two-Point Boundary Value Problems.
Ginn (Blaisdell), Boston.
Keller, H. (1976).
Numerical Solution
of
Two-Point Boundary Value Problems.
Regional Conference Series in Applied Mathematics
24,
Society for In-
dustrial
and
Applied Mathematics, Philadelphia.
Keller, J.,
and
S.
Antman, Eds. (1969). Bifurcation Theory and Nonlinear Eigen-
value Problems. Benjamin, New York.

BIBLIOGRAPHY
449
Krogh, F. (1969),
VODQ/SVDQ/DVDQ-
Variable order integrators for the
numerical solution of ordinary differential equations. Section
314
Sub-
routine Writeup, Jet Propulsion Lab., Pasadena, Calif.
Lambert, J. (1973).
Computational Methods
in
Ordinary Differential Equations.
Wiley, New York.
Lapidus, L., and
W.
Schiesser, Eds.
(1976).
Numerical Methods for Differential
Equations: Recent Developments
in
Algorithms,_ Software. New Applications,
Academic Press, New
York.
Lapidus, L., and J. Seinfeld (1971). Numerical Solution
of
Ordinary Differential
Equations. Academic Press, New York.
Lentini, M., M. Osborne, and
R.
Russell (1985). The close relationship between
methods for solving two-point boundary value problems,
SIAM
J. Numer.
Anal.
22,
280-309.
Melgaard, D.,
and
R. Sincovec (1981). Algorithm 565:
PDETWO/
PSETM/GEARB:
Soluti<>n
of systems of two-dimensional nonlinear par-
tial differential equations,
ACM
Trans. Math. Softw.
7,
126-135.
Miller, R.
K.
and
A.
Michel (1982). Ordinary Differential Equations. Academic
Press, New
York.
Milne,
W.
(1953). Numerical Solution
of
Differential Equations. Wiley, New York.
Ortega,
J., and
W.
Poole (1981).
An
Introduction to Numerical Methods for
Differential Equations, Pitman, New York. ·
Pereyra,
V.
(1979). PASVA3: An adaptive finite difference Fortran program for
first order nonlinear, ordinary differential equation problems. In
B.
Childs,
M.
Scott, J. Daniel,
E.
Denman, and
P.
Nelson (Eds.), Codes for Boundary-
Value Problems
in
Ordinary Differential Equations, pp. 67-88. Lecture
Notes in Computer Science 76, Springer-Verlag, New
York.
Reddien, G. (1979). Projection methods. In B. Childs,
M.
Scott, J. Daniel,
E.
Denman, and
P.
Nelson (Eds.), Codes for Boundary-Value Problems
in
Ordinary Differential Equations, pp. 206-227. Lecture Notes in Computer
Science
76,
Springer-Verlag, New York.
Rheinboldt,
W.
(1984). Differential-algebraic systems as differential equations on
manifolds,
Math. Comput. 43, 473-482.
Rheinboldt,
W.
(1986). Numerical Analysis
of
Parametrized Nonlinear Equations.
Wiley, New York.
Shampine, L. (1985). Local error estimation by doubling, Computing 34, 179-190.
Shampine,
L. (1986). Some practical Runge-Kutta formulas, Math. Comput. 46,
135-150.
Shampine,
L.,
and
L.
Baca (1986). Fixed versus variable order Runge-Kutta,
ACM
Trans. Math. Softw.
12,
1-23.
Shampine, L., and C.
W.
Gear (1979). A user's view
of
solving stiff ordinary
differential equations,
SIAM
Rev.
21,
1-17.
Shampine, L., and M. Gordon (1975). Computer Solution
of
Ordinary Differential
Equations. Freeman, San Francisco.

450 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS
Shampine, L., and
H.
Watts (1976a). Global error estimation for ordinary
differential equations,
ACM
Trans. Math. Softw.
2,
172-186.
Shampine,
L., and H. Watts (1976b). Practical solution of ordinary differential
equations by Runge-Kutta methods.
Sandia Labs. Tech. Rep. SAND
76-0585,
Albuquerque, N.Mex.
Shampine,
L., and H. Watts
(1980).
DEPAC-Design
of a user oriented package
of
ODE
solvers. Sandia National Labs. Rep. SAND79-2374, Albuquerque,
N.Mex.
Shampine,
L., H. Watts, and
S.
Davenport (1976). Solving nonstiff ordinary
differential
equations-
The state of the art,
SIAM
Rev.
18,
376-411.
Sincovec, R., and N. Madsen (1975).
Software for nonlinear partial differential
equations,
ACM
Trans. Math. Softw.
1,
232-260.
Skeel,
R. (1986). Thirteen
ways
to estimate global error, Numer. Math.
48,
1-20.
Stakgold,
I.
(1979). Green's Functions
and
Boundary Value Problems. Wiley, New
York. ·
Stetter, H. (1973). Analysis
of
Discretization Methods for Ordinary Differential
Equations.
Springer-Verlag, New York.
Stoer,
J.,
and
R.
Bulirsch (1980). Introduction to Numerical Analysis. Springer-
Verlag, New
York.
Van der Houwen,
P.
J.
(1977).
Construction
of
Integration Formulas for Initial
Value Problems. North-Holland, Amsterdam.
Widder, D. (1975).
The Heat Equation. Academic Press, New York.
Problems
1.
Draw the direction
field
for
y'
=
x-
y
2
,
and then draw in some sample
solution curves. Attempt to guess the behavior of the solutions
Y(x)
as
X~
00.
2.
Determine Lipschitz constants for the following functions,
as
in (6.1.2).
(a)
f(x,
y)
=
2yjx,
x
~
1
(b)
f(x,
y)
=
tan-
1
(y)
(c)
f(x,
y)
=
(x
3
-
2)
27
/(17x
2
+ 4)
(d)
f(x,
y)
= x - y
2
,
IYI
~
10
3. Convert the following problems to first-order systems.
(a)
y"
-
3y'
+
2y
=
0,
y(O) = 1, y'(O) = 1
