ASM Metals HandBook Vol. 14 - Forming and Forging

Подождите немного. Документ загружается.

Oxidation during sintering or reheating

Excessive contact time

Surface porosity

Low forging temperature

Low preform temperatures

High or low tool temperature

Tool wear

Excessive contact time

Poor tolerances

Temperature variations in tools and preforms

Excessive preform temperature

High preform weight/incorrect distribution

Excessive flash/tool jamming

Improper tool design

Low preform temperature

Excessive forging loads

High preform weight

Oxidation

Low forging temperature/pressure

Low preform weight

Low densities

Die chill

Cracks,laps

Improper tool or preform design

Improper die fill Improper preform weight distribution/material flow

Draft angles, which facilitate forging and ejection in conventional forging, are eliminated in powder forged parts. This

means that greater ejection forces--on the order of 15 to 20% of press capacity as a minimum--are required for the powder

forging of simple shapes. However, the elimination of draft angles permits P/F parts to be forged more closely to net

shape. Figure 10 illustrates the ejection forces required for a P/F gear as a function of residual porosity (Fig. 10a) and

preform temperature (Fig. 10b). To be suitable for powder forging, standard forging presses must be modified to have

stronger ejection systems.

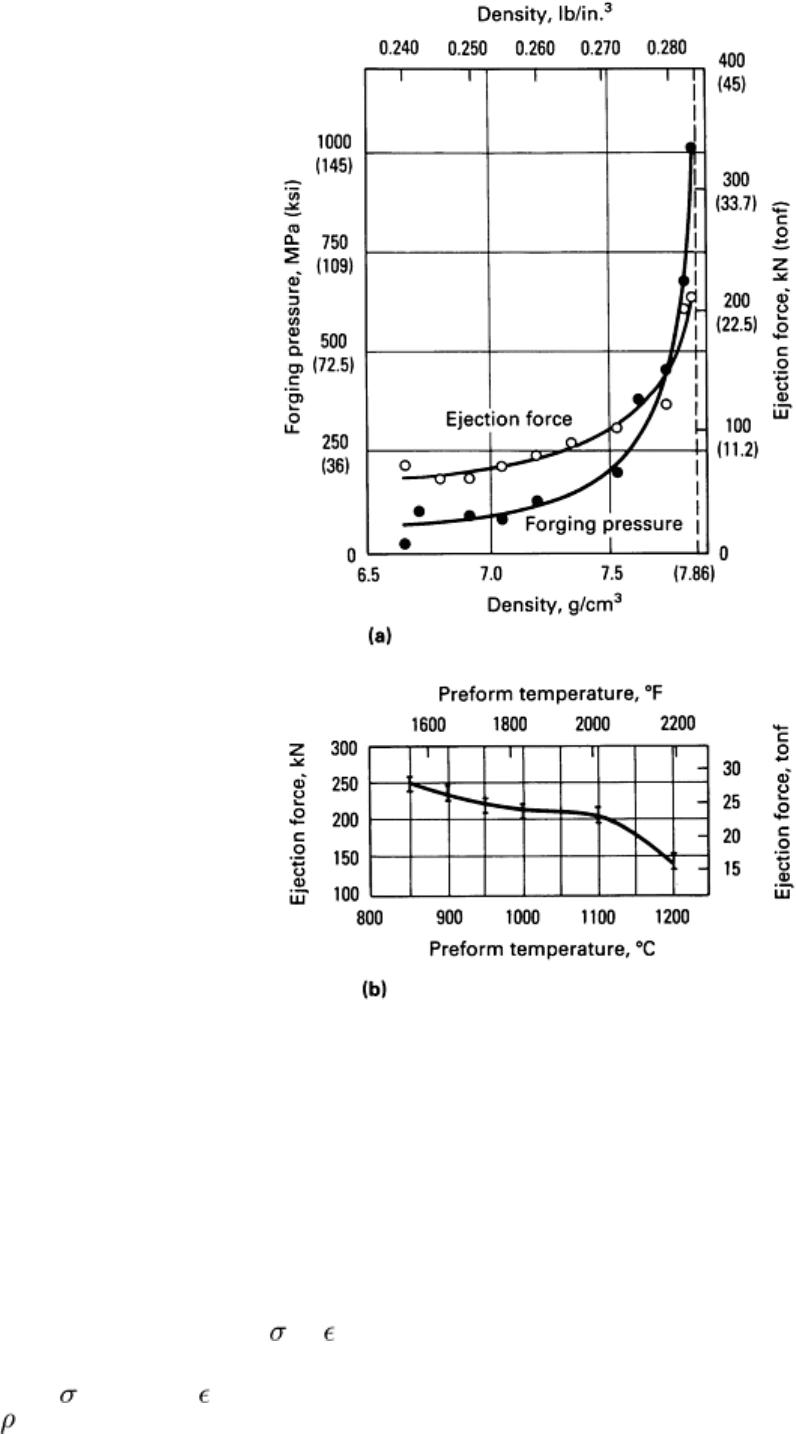
Fig. 10 (a) Forging pressure and ejection force as functions of density for the P/F-

4600 powder forged gear

shown in Fig. 12

. Preform temperature: 1100 °C (2010 °F). (b) Ejection force after forging as a function of

preform temperature for a powder forged gear. Forging pressure ranged from 650 to 1000 MPa (94 to 145 ksi).

The deformation behavior of sintered, porous materials differs from that of wrought materials because porous materials

densify during the forming operation. As a consequence, a porous preform will appear to have a higher rate of work

hardening than its wrought counterpart. The work-hardening exponent, m, can be defined in terms of the true stress-true

strain diagram:

= K

(Eq 1)

where is true stress, is true strain, and K is a proportionality constant. An empirical relationship between m and density

for a ferrous preform has been shown (Ref 44):

m = 0.31ρ

-1.91

(Eq 2)

where is expressed as a fraction of the density of pore-free material. The value of m for pore-free pure iron is 0.31, and

any excess over this value for porous iron is due to geometric work hardening.

A further consequence of the densification of porous preforms during deformation is reflected in Poisson's ratio for the

porous material. Poisson's ratio is a measure of the lateral flow behavior of a material; for compression of a cylinder, it is

expressed as diametral strain

divided by height strain -

. For a pore-free material, Poisson's ratio for plastic

deformation is 0.5. This is a direct result of the fact that the volume of the material remains constant during

deformation. For example, equating the volume of a cylinder before and after deformation (Ref 44):

[ )/4] = H

[( )/4]

(Eq 3)

where H

and H

are initial and final cylinder heights, respectively, and D

and D

are initial and final cylinder diameters,

respectively. Dividing by H

yields:

= (D

)

(Eq 4)

and taking logarithms

ln (H

) = ln (D

)

= 2 ln (D

)

(Eq 5)

= 2

(Eq 6)

and, from the definition of Poisson's ratio:

(Eq 7)

During compressive deformation of a sintered metal powder preform, some material flows into the pores, and there is a

volume decrease. For a given reduction in height, the diameter of a sintered P/M cylinder will expand less than that of an

identical cylinder of a pore-free material. Poisson's ratio for a P/M preform will therefore be less than 0.5 and will be a

function of the pore volume fraction. H.A. Kuhn (Ref 45) has established an empirical relationship between Poisson's

ratio and part density:

= 0.5

(Eq 8)

The best fit to experimental data is obtained with the exponent a = 1.92 for room-temperature deformation and a = 2.0 for

hot deformation. The slight difference in this exponent may be due to work hardening (Ref 44).

In deformation processing of materials, plasticity theory is useful for calculating forming pressures and stress

distributions. The above mentioned idiosyncrasies in the deformation behavior of sintered, porous materials have been

taken into account in the development of a plasticity theory for porous materials. This has been of benefit in applying

workability analysis to porous preforms (Ref 31, 44, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59).

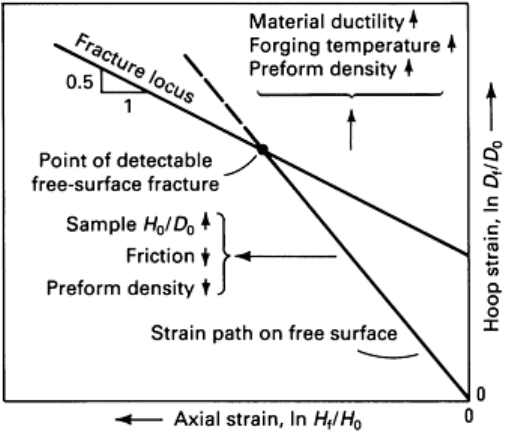
A typical workability line is shown in Fig. 11, which also indicates the way processing variables affect the location of the

line. The line has a slope of -0.5, and workability improves as the plane strain intercept (y-axis intercept) value increases.

For a given material, workability can be improved through either temperature adjustment or a change in preform density.

Figure 12(b) to (e) show the effects of temperature and pressure on the densification and forming of the powder forged

gear shown in Fig. 12(a) (Ref 61). While Fig. 12(b) to (e) indicate that higher temperatures reduce the forging pressures

required, Fig. 13 illustrates a region of forging pressure at lower temperatures that is comparable to that for higher-

temperature forging. The ability to forge at lower temperatures may be beneficial in extending the life of the forging dies.

Fig. 11 Effects of forging variables on the workability of porous preforms in hot forging. Source: Ref 60.

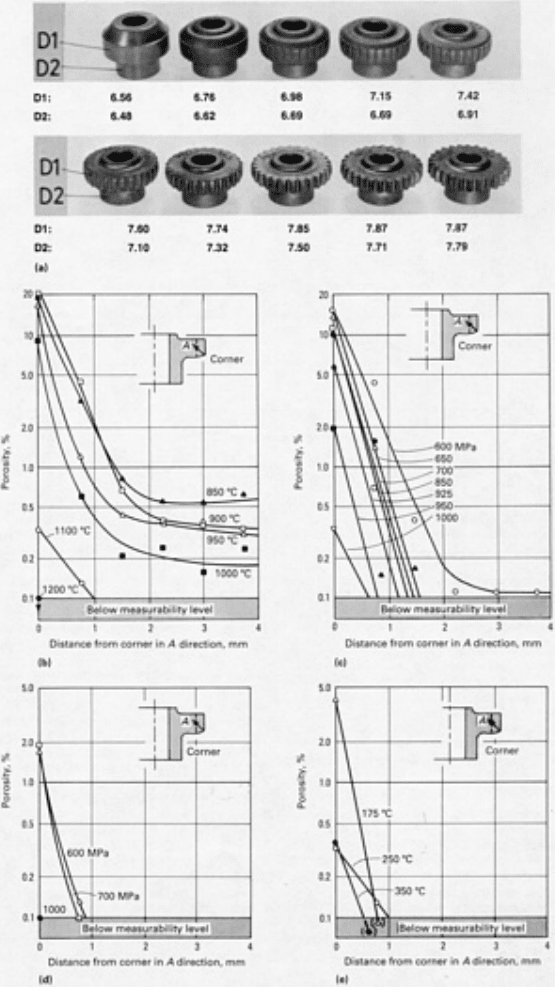
Fig. 12 Influence of process variables on re

sidual porosity in critical corner areas of a powder forged gear

tooth. (a) Powder forged gear; D1 and D2 are average densities in grams per cubic centimeter. (b) Preform

temperature at a forging pressure of 1000 MPa (145 ksi). (c) and (d) Forging pressure

at preform temperatures

of 1100 °C (2010 °F) and 1200 °C (2190 °F), respectively. (e) Die temperature at a forging pressure of 1000

MPa (145 ksi) and a preform temperature of 1100 °C (2010 °F). Source: Ref 43, 61.

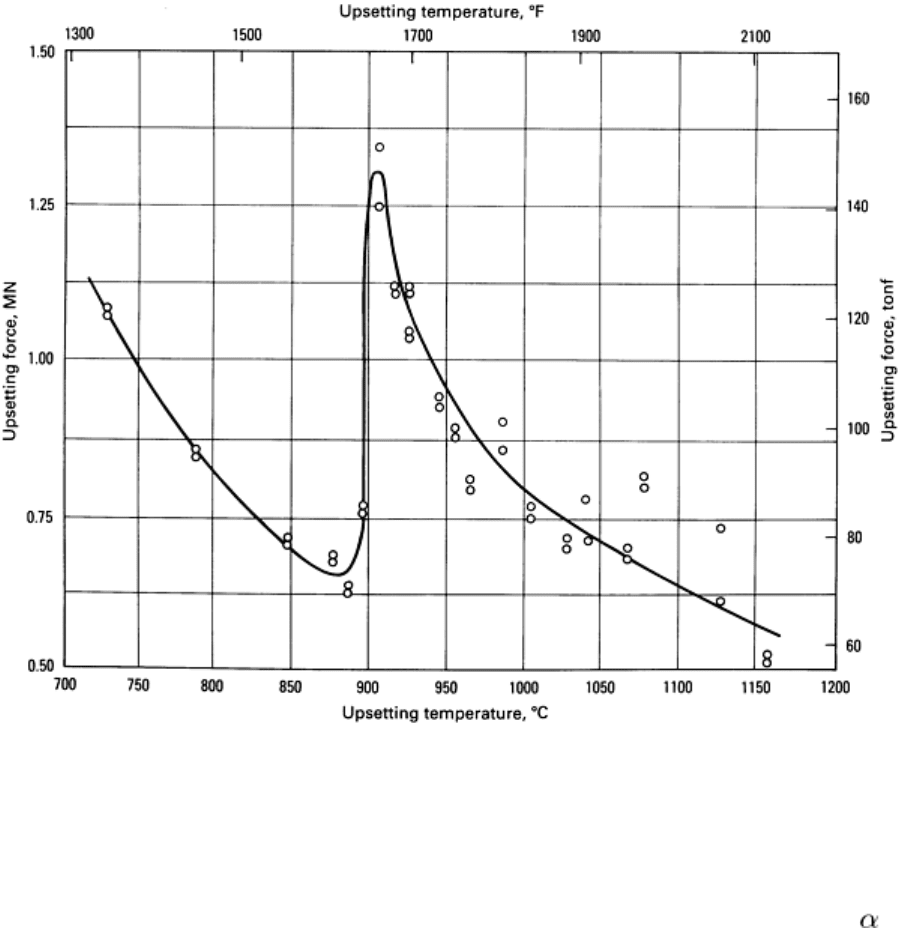
Fig. 13 Force required for a 50% reduction in height of water-

atomized iron powder preforms as a function of

deformation temperature. Source: Ref 62.

The data presented in Fig. 13 relate to a pure iron with no added graphite. The dramatic increase in the force required for

densification around 900 °C (1650 °F) is due to the phase transformation from body-centered cubic (bcc) iron to face-

centered cubic (fcc) austenite. In this temperature range, the flow stress of austenite is higher than that of ferrite.

However, although materials are fully austenitic at conventional forging temperatures (1000 to 1130 °C, or 1830 to 2065

°F), the flow stress of austenite at 1100 °C (2010 °F) is less than that of ferrite at 850 °C (1560 °F).

A similar low flow stress regime has been observed for prealloyed material (Fig. 14). However, depending on the amount

of solution of graphite, the dip in the flow stress versus temperature curve becomes less pronounced and eventually is no

longer observed. The presence of carbon in solution alters the phase distribution, and the observed flow stress depends on

the relative proportions of ferrite and austenite in the microstructure.

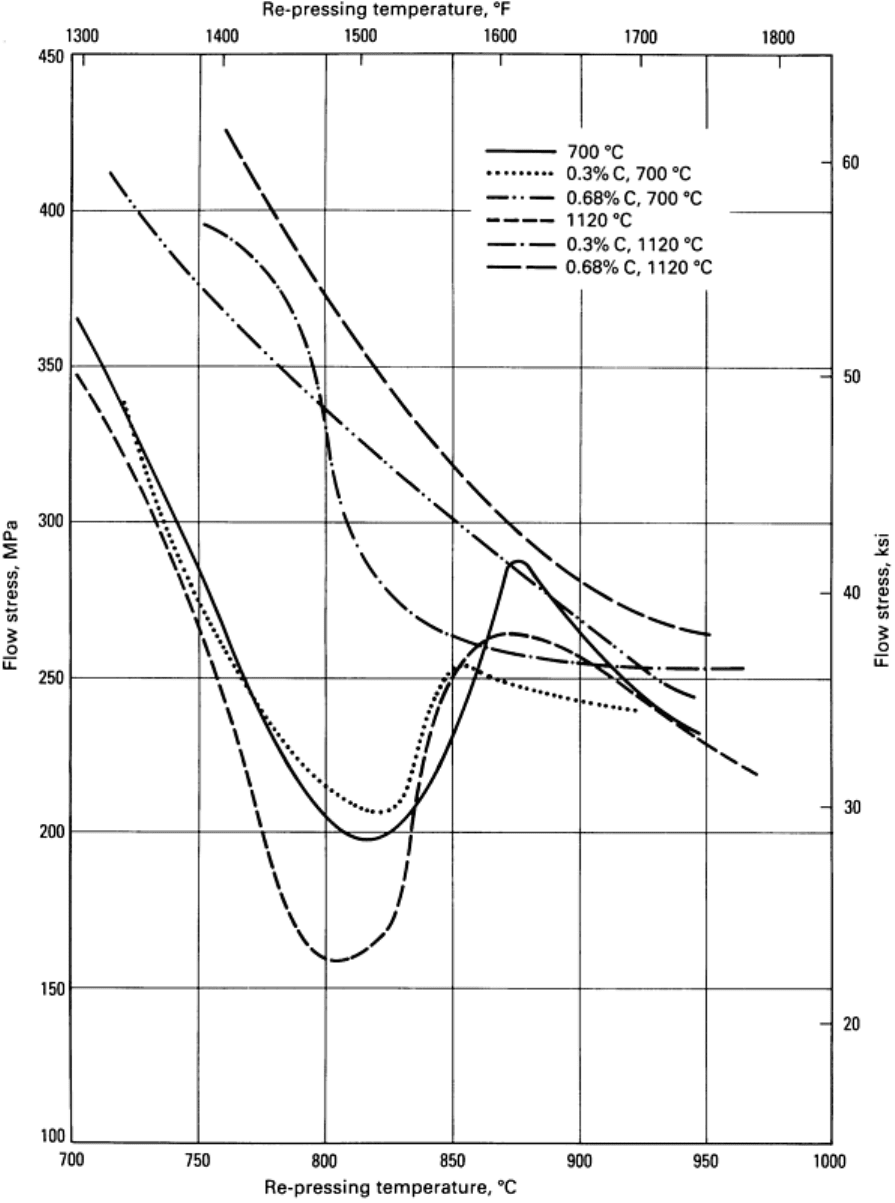
Fig. 14 Influence of hot re-pressing temperature on flow stress for P/F-4600 at various carbon

contents and

presintering temperatures. Data are for density of 7.4 g/cm

(0.267 lb/in.

). Source: Ref 63, 64.

In order to take any advantage of the low flow stress, the thermomechanical processing of preforms that contain added

graphite must therefore be such that the graphite does not go into solution. Even under such conditions, in the data

reported by Q. Jiazhong, O. Grinder, and Y. Nilsson (Ref 65), the mechanical properties of low temperature forged

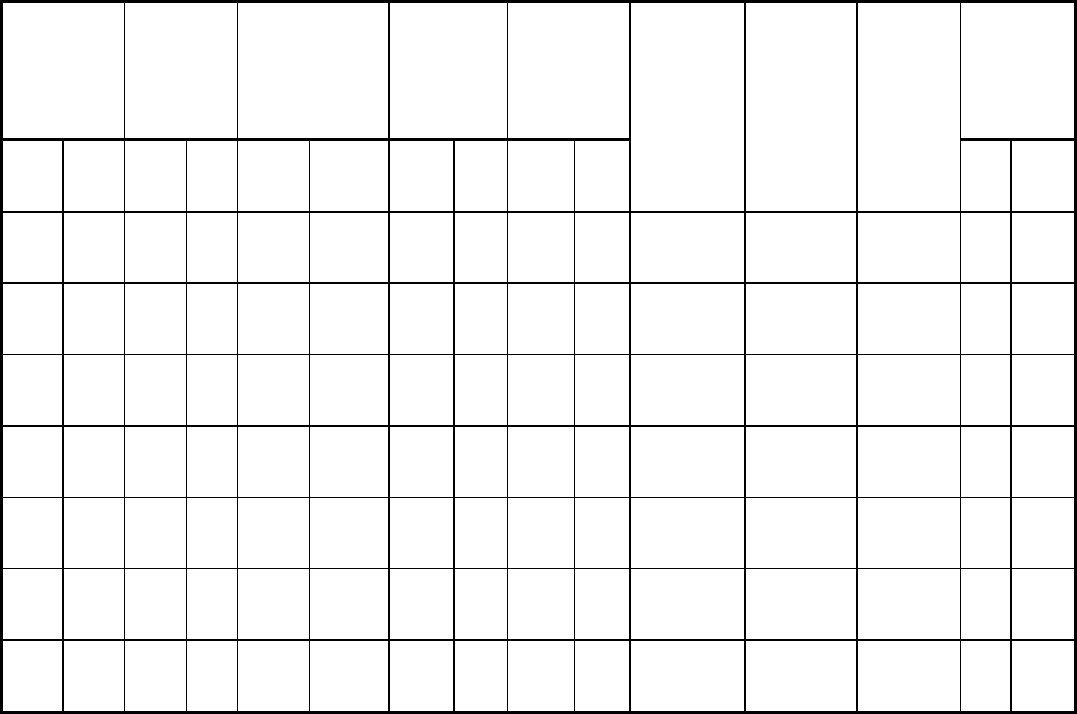
material are considerably inferior to those of material forged at higher temperatures (Table 2). The low-temperature

forging resulted in incomplete densification, and this degraded the mechanical properties. G. Bockstiegel and H. Olsen

observed a similar dependence of forged density on preform temperature (Ref 66). They pointed out that the presence of

free graphite might impede densification. During subsequent heat treatment, when the graphite goes into solution, it could

leave fine porosity, which would degrade the mechanical properties of the material.

Table 2 Tensile and impact properties of P/F-4600 hot re-pressed at two temperatures

Re-pressing

temperature

Re-

pressing

stress

Re-pressed

density

0.2% offset

yield

strength

Ultimate

tensile

strength

Charpy V-

notch

impact

energy

°C °F MPa

ksi g/cm

lb/in.

MPa

ksi MPa ksi

Elongation,

Reduction

area, %

Hardness,

(a)

ft · lb

870 1600

406 59 7.65 0.276 1156 168

1634 237 2.6 2.8 519 2.9

2.13

870 1600

565 82 7.72 0.279 1243 180

1641 238 2.1 2.8 538 2.8

2.06

870 1600

741 107

7.78 0.281 1316 191

1702 247 2.4 2.4 564 3.1

2.29

870 1600

943 137

7.79 0.282 1349 196

1705 248 2.3 2.4 562 3.5

2.58

1120

2050

344 50 7.83 0.283 1364 198

1750 254 6.4 20.5 549 6.8

5.01

1120

2050

593 86 7.86 0.2840 1450 210

1777 258 6.7 17.3 566 6.2

4.57

1120

2050

856 124

7.87 0.2844 1592 231

1782 259 5.3 14.1 565 6.2

4.57

(a)

30-kgf load

Metal flow can cause surface fractures. These are generally associated with contact between the deforming preform and

the forging tooling. Surface fracture problems may be avoided by changing the preform geometry or the lubrication

conditions.

Frictional constraint at the interface between the preform and the forging die generates undesirable stress states in the

preform that can lead to fracture. The types of fracture encountered in powder forging are:

• Free-surface fracture

• Die contact surface fracture

• Internal fracture

Production of metallurgically sound forgings requires the prediction and elimination of fracture. An excellent review of

the subject is given in Ref 44, 47, 57, and 58.

Tool Design. In order to produce sound forged components, the forging tooling must be designed to take into account:

• Preform temperature

• Die temperature

• Forging pressure

• The elastic strain of the die

• The elastic/plastic strain of the forging

• The temperature of the part upon ejection

• The elastic strain of the forging upon ejection

• The contraction of the forging during cooling

• Tool wear

Specified part dimensional tolerances can only be met when the above parameters have been taken into account.

However, there is still some flexibility in the control of forged part dimensions even after die dimensions have been

selected. Higher preform ejection temperatures result in greater shrinkage during cooling. Increases in die temperature

expand the die cavity and thus increase the size of the forged part. Therefore, if the forgings are undersize for a given set

of forging conditions, a lower preform preheat temperature and/or a higher die preheat temperature can be used to

produce larger parts. On the other hand, if the forged parts are oversize, the preform preheat temperature could be raised

and/or the die temperature lowered to bring the parts to the desired size.

Secondary Operations. In general, the secondary operations applied to conventional components such as plating and

peening, may be applied to powder forged components. The most commonly used secondary operations involve

deburring, heat treating, and machining.

The powder forged components may require deburring or machining to remove limited amounts of flash formed between

the punches and the die. This operation is considerably less extensive than that required for wrought forgings.

The heat treatment of P/M products is the same as that required for conventionally processed materials of similar

composition. The most common heat-treating practices involve treatments such as carburizing, quench-and-temper cycles,

or continuous-cooling transformations.

The amount of machining required for P/F components is generally less than the amount required for conventional

forgings because of the improved dimensional tolerances, shown in Table 3. Standard machining operations may be used

to achieve final dimensions and surface finish (Ref 67). One of the main economic benefits of powder forging is the

reduced amount of machining required, as illustrated in Fig. 15.

Table 3 Comparison of powder forging with competitive processes

Range of weights

Process

kg lb

Height-

to-

diameter

ratio

Shape Material

use, %

Surface

roughness

μm

Quantity

required

for economical

production

(a)

Cost per

unit

(b)

Powder

forging

0.1-5 0.22-11

1 No large variations in cross

section; openings limited

100 5-15 20,000

200

Precision

forging

0.3-5 0.66-11

2 Any; openings limited 80-90 10-20 20,000

200

Cold forging

0.01-

0.022-

Not

limited

Mostly rotational symmetry 95-100 1-10 5,000

150

Precision

casting

0.1-10 0.22-22

Not

limited

Any; no limits on openings 70-90 10-30 2,000

100

Sintering 0.01-5 0.022-

1 No large variations in cross

section; openings limited

100 1-30 5,000

100

Drop

forging

0.05-

1000

0.11-

2200

Not

limited

Any; openings limited 50-70 30-100 1,000 150

(a)

For 0.5 kg (1.1 lb) parts.

(b)

Sintering = 100%

Fig. 15

Comparison of material use for a conventionally forged reverse idler gear (top) and the equivalent

powder forged part (bottom). Material yield in conventional forging is 31%; that for powder forging is 86%.

1 lb

= 453.6 g. Source: Ref 61.

In general, pore-free P/F materials machine as readily as conventional forgings processed to achieve identical

composition, structure, and hardness. Difficulties are encountered, however, if P/F components are machined with the

same cutting speeds, feed rates, and tool types as conventional components. These differences in machinability have been

related to inclusion types and microporosity (Ref 16, 68). These studies conclude that P/F materials can exhibit equal or

greater machinability than wrought steels. Improved machinability can be accomplished by the addition of solid

lubricants such as manganese sulfide.

However, the presence of microporosity and low-density noncritical areas in P/F components leads to reduced

machinability. The machinability behavior for these areas is similar to that of conventional P/M materials (Ref 69). The

overall machinability of a powder forged component may be said to depend on the amount, type, size, shape, and

dispersion of inclusions and/or porosity, as well as on the alloy and heat-treated structure.

References cited in this section

4. G. Bockstiegel, Powder Forging--Development of the Technology and Its Acceptance in North A

merica,

Japan, and West Europe, in Powder Metallurgy 1986--State of the Art,

Vol 2, Powder Metallurgy in Science

and Practical Technology series, Verlag Schmid, 1986, p 239

8. W.J. Huppmann and M. Hirschvogel, Powder Forging, Review 233, Int. Met. Rev., (No. 5), 1978, p 209

16.

R. Koos and G. Bockstiegel, The Influence of Heat Treatment, Inclusions and Porosity on the Machinability

of Powder Forged Steel, Prog. Powder Metall., Vol 37, 1981, p 145

25.

G. Bockstiegel, E. Dittrich, and H. Cremer, Experience

s With an Automatic Powder Forging Line, in