Асанов А.З. Введение в математическое моделирование динамических систем
Подождите немного. Документ загружается.

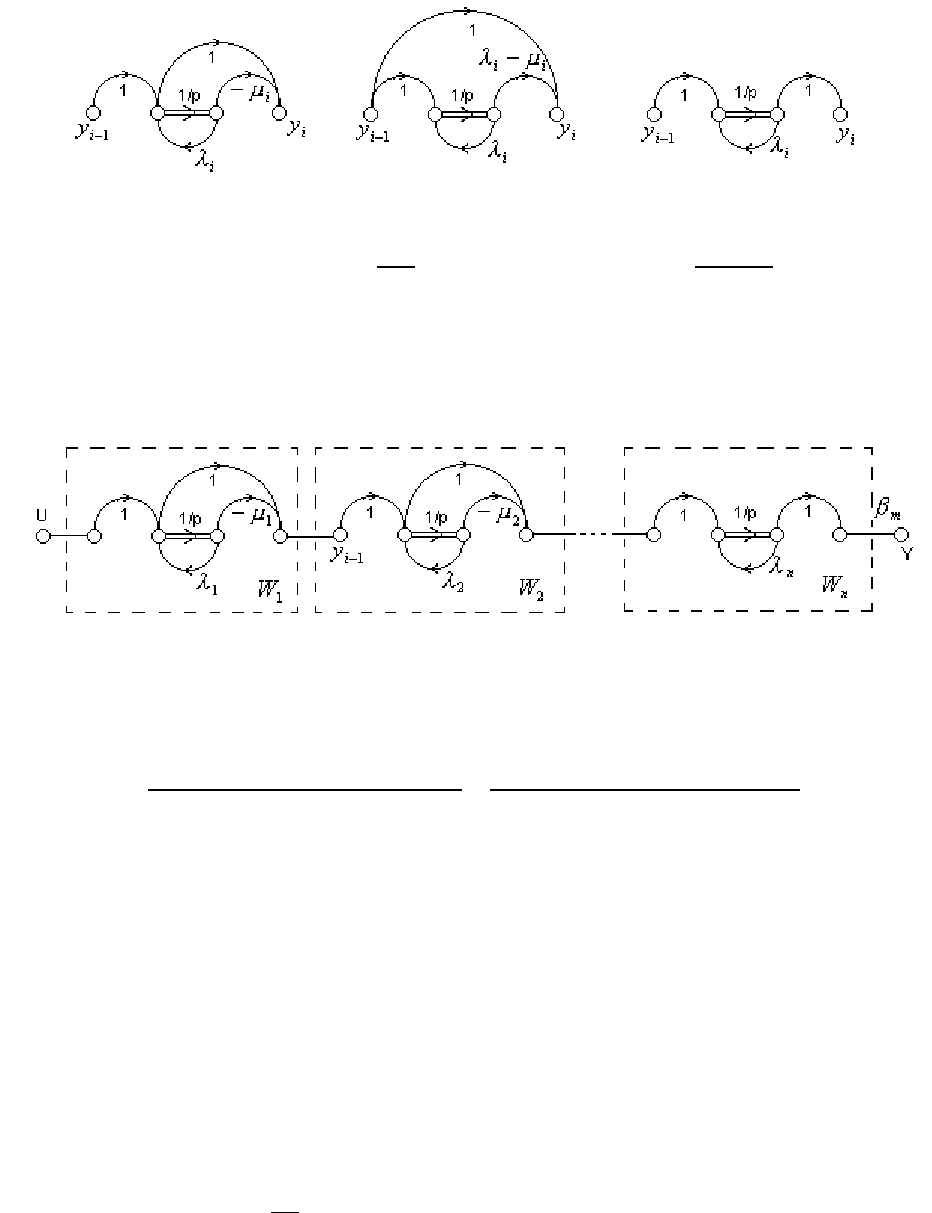
Отметим немаловажное обстоятельство – структура последовательной
КФ не зависит от наличия кратных корней характеристического полинома.
а) б) в)
Рис. 5.9.15. Реализации простых дробей I порядка
а) , б)
W при ()
i
p 1,i ; в) W при m= p()
i
1,im n=+
Рис. 5.9.16. Граф последовательной КФ системы (5.9.25)
Матричное описание последовательной КФ рассмотрим на реализации
двух крайних случаев:
и 0m = 1mn
=
− . Пусть 0m
=
, тогда
00
1
11012
nn
n n
W( p)
p
p ... p ( p )( p )...( p )
β
β
α
αα λ λ λ
−
−
==
++++−− −
. (5.9.26)
Реализация КФ будет представлять собой последовательное соединение
апериодических звеньев I порядка, описываемое следующей системой
уравнений
111
2221
0
1
n
nnnn
xxU
xxx
Yx
....................
xxx
λ
λ
β
λ
−
=+
⎧
⎪
=+
⎪
=
⎨
⎪
⎪
=+
⎩
Матричная запись этой системы
d
A
XBU YCX
dt
=+ =
характеризуется матрицами
177

1
2
3
0
00 00 0
1
1000
0
01 00 0
0
000 1
0
T
n
...
....
A...,B,C
... ... ... ... ... ... ...
...
...
0
λ
λ
λ
λ
β
⎡⎤
⎡⎤
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
==
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎣⎦
⎣⎦
⎡⎤
⎢⎥
⎢⎥
⎢⎥
=
⎢⎥
⎢⎥
⎢⎥
⎣⎦
.
Если
, то 1mn=−
10 1 11
1
11011
m
mn
nn
nn
p... p p p
W( p) ...
pp...p ppp
βββ µµ
n
n
β
α
αα λ λ λ
−−
−
−−
++ + − −
==
++++−−−
.
Уравнения в пространстве состояний в общем случае имеют вид
111
22211
3331122
1
11 2 2 1 1
ii
nn
nnn nn
xxU
xxxU
xxxxU
Yx
..........................................
x x x x ... x U
i
λ
λν
ν
λµ
λνν
β
λνν ν
−
−−
=+
⎧
⎪
=++
⎪
=
−
⎪
=+++
⎨
=
⎪
⎪
=++++ +
⎪
⎩
Матричная запись системы в этом случае характеризуется матрицами
1
12
123
12 3 1 1
00...0 0 0
1
0... 0 0 0
1
.. 0 0 , , 0
1
... ... ... .. ... ... ...
...
..
1
T
nn n
AB
v
C
λ
νλ
νν λ
νννλ β
−−
⎡⎤
⎡⎤
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
==
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎣⎦
⎣⎦
⎡⎤
⎢⎥
⎢⎥
⎢⎥
=
⎢⎥
⎢⎥
⎢⎥
⎣⎦
. (5.9.27)
Таким образом, матрица
A
последовательной канонической формы при
имеет треугольный вид, а при 1mn=− 0m
=
– двухдиагональный.
Случаи
1 характеризуются промежуточной структурой
матриц
1mn≤≤−
A
,B, C
. Наличие у передаточной функции комплексных нулей
или полюсов усложняет структуру реализации последовательной
канонической формы. В этом случае кроме блоков I порядка появляются
и блоки II порядка с передаточными функциями одного из трех типов:
2
10
1
W( p)
pp
α
α
=
++
,
2
10
i
p
W( p)
pp
µ
α
α
−
=
+
+
,
2
10
2
10
pp
W( p)
pp
β
β
α
α
++
=
++
.
178
6. Математические модели динамических систем в
форме проблемных матриц
Решение многих задач анализа и синтеза многосвязных систем
сопряжено с целым рядом особенностей и трудностей, при разрешении
которых традиционные подходы малоэффективны.
Одним из современных концепций решения подобных задач является
формализация математических моделей линейных динамических систем,
которая позволяла бы наиболее полно использовать достижения современной
алгебры.
В новой концепции, называемой технологией вложения
систем, таким
формализованным представлением моделей систем являются матема-
тические объекты в виде специфических матриц, называемых проблемными
матрицами, или, кратко, проматрицами. Проматрица в полной мере
описывает структуру и свойства исследуемой линейной системы, и на ее
основе можно ставить и решать различные задачи теории систем.
6.1. Математическая модель линейной системы в форме
проматрицы
Вначале рассмотрим задачу моделирования динамической системы.
Пусть такая система состоит из одной подсистемы – объекта управления.
Ставится задача описать ее структуру и свойства. Задача моделирования
является среди прочих простейшей, в других случаях система будет состоять
из нескольких подсистем.
Под задачей моделирования будем понимать представление заданной
модели системы в такой форме, которая наиболее
полно отражает все си-
стемные свойства этой модели и которая удобна для использования
существующих методов анализа динамических систем.
Рассмотрим динамическую систему в пространстве состояний,
представленную в операторной форме:
0
() () () (),
() () ().
p
xp Axp Bup x p
yp Cxp Dup
=
++
=+
(6.1.1)
где
и – изображения входного и выходного
векторов;
,1
()
s
up
,1
()
m
yp
,1
()
s
ut
,1
()
m
yt
,1
()
n
x
p – изображение вектора состояний
,1
()
n
x
t ;
0
x
– вектор
179
начальных условий; постоянные матрицы
,nn
A
,
,ns
B
, ,
,mn
C
,ms
D
характеризуют
динамические свойства системы.
В общем случае количество уравнений в формуле (6.1.1) не совпадает с
числом фигурирующих в ней переменных. Это связано с наличием внешнего
воздействия
, не зависящего от других переменных. Системная матрица
Розенброка, соответствующая (6.1.1), имеет размер
()ut
(
)( )
nm ns+×+
⎡
⎤
⎣
⎦
, т.е.
является прямоугольной. Это обстоятельство создает большие затруднения
при анализе такой системы с помощью методов, основанных на
алгебраических процедурах вычисления определителей, собственных значе-
ний и собственных векторов квадратных числовых матриц.
Для составления проматрицы дополним эту систему уравнением
(регуляризирующим тождеством, пополнением) вида
)()( pupu
=
, (6.1.2)
не влияющим на содержание задачи, представленной уравнениями (6.1.1).
Затем полученную систему уравнений
0
()()()
() () (),
() ()
n
p
IAxpBupx
yp Cxp Dup
up up
−=
=+
=
+
m
(6.1.3)
запишем в блочно-матричном виде:
,0
,1
,,
0()
() 0
0 0 () ()
nnm
m
sn sm s
p
IA Bxp x
CI Dyp
I
up up
⎡⎤
−−
⎡
⎤⎡ ⎤
⎢⎥
⎢
⎥⎢ ⎥
−−=
⎢⎥
⎢
⎥⎢ ⎥
⎢⎥
⎢
⎥⎢ ⎥
⎣
⎦⎣ ⎦
⎣⎦
(3.1.4)
Определение 6.1
. Матрица-столбец, составленная из субвекторов,
представляющих собой вектор входных воздействий
, вектор выходных
реакций
и вектор внутренних переменных
()up
()yp ()
x
p
системы,
()
() ()
()
x
p
Yp yp
up
⎡
⎤
⎢
⎥
=
⎢
⎥
⎢
⎥
⎣
⎦
(6.1.5)
называется
обобщенным выходом системы, а матрица-столбец,
составленная из субвекторов, представляющих собой вектор входных
воздействий
, вектор начальных условий
()up
0
x
и нулевой вектор ,
,1
0
m
0
,1
0
()
m
x
Up
up
⎡⎤
⎢⎥
=
⎢⎥
⎢⎥
⎣⎦
()
(6.1.6)
180
называется обобщенным входом системы.
Очевидно, что последовательности субвекторов обобщенного выхода
и обобщенного входа связаны с порядком следования уравнений
(6.1.3). При составлении уравнений типа (6.1.3) рекомендуется выбирать
такую очередность уравнений модели (субвекторов обобщенного входа
) и слагаемых в уравнениях (субвекторов обобщенного выхода )
системы, чтобы блочная матрица полиномиальных коэффициентов имела
правильную структуру, при которой главная диагональ содержит только
невырожденные блоки. Это существенно упростит дальнейшие исследования
динамических систем.
()Yp ()Up
()Up ()Yp
Перепишем уравнение (6.1.4) в виде
()() ()pY p U p
Ω
=
. (6.1.7)
Определение 6.2.
Блочно-матричное уравнение (3.1.7), связывающее
обобщенный вход
и обобщенный выход системы, называется
обобщенным уравнением линейной системы.
()Up ()Yp
Определение 6.3. Квадратная полиномиальная матрица
, которая
обобщенному выходу
ставит в соответствие обобщенный вход
системы по формуле (6.1.7), называется
проблемной матрицей или,
кратко,
проматрицей рассматриваемой системы в конкретной задаче.
()pΩ
()Yp ()Up
Таким образом, в задаче моделирования в соответствии с формулой
(6.1.4) проматрица размера
(
)
(
)
nms nms++×++
⎡
⎤
⎣
⎦
имеет вид
,, ,
,
,,
0
()
00
nnnnm ns
mn m ms
sn sm s
pI A B
pCID
I
,
⎡
⎤
−−
⎢
⎥
Ω=− −
⎢
⎥
⎢
⎥
⎣
⎦
(6.1.8)
Определение 6.4.
Блочная матрица (6.1.8) называется проматрицей
моделирования для объекта, заданного в пространстве состояний
постоянными матрицами
A
, , C , . B D
Анализ обобщенного уравнения динамики линейной системы 6.1.7) и
матриц (6.1.5), (6.1.6), (6.1.8) показывает следующее:
1)
структура обобщенных входов и выходов (размещение
субвекторов) однозначно связана со структурой проматрицы
()Up ()Yp
()p
Ω
(размещение и содержание блоков). Поэтому в большинстве случаев для
полного представления структуры системы достаточно приводить только
181
проматрицу, что позволяет говорить о математической модели системы в
форме проматрицы;
2)
проматрица обладает обобщающим характером, поскольку любой
исследуемый элемент линейной динамической системы обязательно
является элементом или составной частью элемента проматрицы;
3)
для каждой решаемой задачи проматрица
()p
Ω
будет иметь свое
название, структуру и элементы, определяемые содержанием этой задачи;
4)
формулировка и решение каждой задачи сводится к разрешению про-
матрицы относительно некоторых ее элементов (или нужной комбинации
этих элементов с другими).
Общие свойства проматрицы
:
1.
Квадратность.
2.
Невырожденность.
Эти свойства квадратности и невырожденности (т.е.
0)(de
t
≠Ω
p
)
обеспечивают проматрице любой задачи двустороннюю обратимость, так что
обратная к ней матрица всегда единственна. В основе этого важнейшего
свойства проматриц лежит введенное дополнительное регуляризирующее
тождество (6.1.2).
3.
Автономность, т.е. все уравнения (коэффициенты исходных
уравнений) представлены в проматрице самостоятельными строками-
уравнениями.
4.
Разреженность, т.е. большое количество нулевых элементов
проматрицы, что может значительно облегчить выполнение вычислительных
процедур.
5.
Универсальность – применимость для любой формы модели, т.е. в
любой задаче исследуемую или синтезируемую систему можно представить
в форме обобщенного уравнения (6.1.8) и, следовательно, соответствующей
проматрицы.
Продемонстрируем последнее свойство на примере все той же задачи
моделирования, но с другими представлениями модели системы.
Пусть имеется запись системы в форме левой факторизации
)()()()()(
0
pypupBpypA
LL
+
=
.
Дополним ее формальным регуляризирующим тождеством
)()( pupu
=
.
182
Объединяя уравнения, получаем
)(
0
)(
)(
)(
)(
)(
)(
0
)()(
pUpY
p
S
LL
pu
py
pu
py
I
pBpA
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
−
Ω
(6.1.9)
уравнение с проматрицей для левой факторизации.
Определение 6.5. Блочная матрица
() ()
()
0
LL
S
A
pBp
p
I
−
⎡
⎤
Ω=
⎢
⎥
⎣
⎦
(6.1.10)
называется
проматрицей задачи моделирования для объекта, заданного в
форме левой факторизации парой полиномиальных матриц (
()
L
A
p
, ).
()
L
Bp
Аналогично для случая правой факторизации можно получить
0
()() () ()
() ()()
R
R
A
pv p u p v p
yp B pvp
=
+
=
(6.1.11)
Допишем к формуле (6.1.11) регуляризирующее тождество (6.1.2) и
запишем полученную систему в виде обобщенного уравнения линейной
системы
,0
,,
,,
() 0 () ()
() 0 () 0
00 ()(
Rsms
Rmms m
ss sm s
1
)
A
pIvpv
Bp I yp
p
I
up up
⎡⎤
−
⎡
⎤⎡ ⎤
⎢⎥
⎢
⎥⎢ ⎥
−=
⎢⎥
⎢
⎥⎢ ⎥
⎢⎥
⎢
⎥⎢ ⎥
⎣
⎦⎣ ⎦
⎣⎦
,
где матрица
определяется тождеством
()pΩ
,
,
,,
() 0
() () 0
00
R
sm s
R
mms
ss sm s
A
pI
pBpI
I
⎡
⎤
−
⎢
⎥
Ω=−
⎢
⎥
⎢
⎥
⎣
⎦
. (6.1.12)
Определение 6.6. Блочная матрица (3.1.12) называется
проматрицей
задачи моделирования
для объекта, заданного в форме правой
факторизации парой полиномиальных матриц (
()
R
A
p
, ).
()
R
Bp
При нулевых начальных условиях
0
() 0vp
=
систему (6.1.12) можно
представить матричным уравнением
,
,1
()
() 0
()
0
()
()
Rsm
m
Rm
up
Ap
vp
Bp I
yp
⎡
⎤
⎡⎤
⎡⎤
=
⎢
⎥
⎢⎥
⎢⎥
−
⎣⎦
⎣⎦
⎣
⎦
.
Здесь матрица полиномиальных коэффициентов всегда обратима в силу
обратимости по определению матричного знаменателя
()
R
A
p
. Поэтому даже
183
без регуляризирующего тождества (6.1.2) это уравнение можно
рассматривать как обобщенное уравнение динамики системы. В этом случае
проматрица моделирования системы (6.1.11) будет определяться тождеством
,
() 0
()
()
Rs
Rm
Ap
p
m
B
pI
⎡⎤
′
Ω=
⎢
−
⎣⎦
⎥
. (3.1.13)
Проматрица (6.1.13) является наиболее компактным вариантом
представления динамических систем, модели которых записаны в форме
правой факторизации (но с нулевыми начальными условиями).
6.2. Проматрицы типовых соединений систем
Достаточно часто динамическую систему удается представить как
совокупность подсистем, объединенных по некоторым правилам. Рассмот-
рим составные многосвязные темы, возникающие в результате типового
соединения двух динамических подсистем. Математические модели
подсистем могут быть различными по форме, но наиболее компактные
записи получаются в случае использования операторных уравнений в форме
левой факторизации
0
11 11 1
0
22 22 2
() () () () ()
() () () () ()
A
py p B pu p y p
A
py p B pu p y p
=+
=+
. (6.2.1)
Количество входов
1
s
,
2
s
и выходов , обеих подсистем должны быть
согласованы в соответствии с каждым типом их соединения.
1
m
2
m
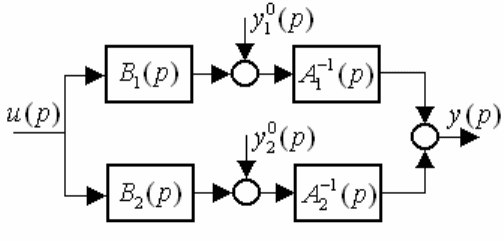
Параллельное соединение (рис.6.2.1). Для параллельного соединения
подсистем (6.2.1) характерно совпадение количества входов и количества
выходов, т.е.
12
s
s=
и .
Рис.6.2.1. Структура параллельного соединения двух подсистем
В этом случае уравнения взаимо зи между подсистемами можно
запи
12
mm=
свя
сать следующим образом:
184

() ()up up==()up
,
12
() () ()yp y p y p
=
+
.
Тогда уравнения системы можн ставить в следующем виде:
() () () () (),
() () () 0.
о пред
0
11 11 1
() () () () (),
A
py p B pu p y p
−=
0
22 22 2
12
A
py p B pu p y p
yp y p y p
−=
−−=
(6.2.2)
Дополним уравнения (6.2.2) регуляризирующим тождеством (6.1.2) и
запи
1
1
1
0
22
2
2
0 ()
()
()
0()0()
()
()
0
()
0
000
()
()
mmm
s
Bp
yp
yp
Ap Bp
yp
yp
III
yp
I
up
up
−
⎡⎤
⎤
⎡⎤
⎢⎥
⎢⎥
⎢⎥
−
⎢⎥
⎢⎥
⎢⎥
=
⎢⎥
⎢⎥
⎢⎥
−−
⎢⎥
⎢⎥
⎢⎥
⎣⎦
⎣⎦
⎣⎦
. (6.2.3)
Отсюда видно, что проматрица параллельного соединения двух
динамических л
)
шем полученную систему уравнений как блочно-матричное обобщенное
уравнение линейной системы
1
() 0Ap
⎡
0
систем, заданных операторными уравнениями в форме евой
факторизации, имеет вид
11
22
() 0 0 ()
0()0(
()
0
000
mmm
s
A
pBp
A
pB
p
III
I
+
−
p
⎡
⎤
⎢
⎥
−
⎢
⎥
Ω=
⎢
⎥
−−
⎢
⎥
⎣
⎦
.
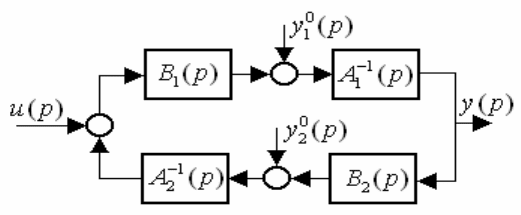
Последовательное соединение (рис.6.2.2). Для последовательного со-
единения двух подсистем характерно то, что количество выходов первой
подсистемы равно количеству входов второй, т.е.
12
ms
=
.
Рис.3.2.2. Структура последовательного соединения двух подсистем
Ура ми
Уравнения объединенной системы принимают вид
() () () () (),
() () 0.
внение взаимосвязи подсистем можно представить равенства
21 1 2
() (), () (), () ()up yp up up yp yp== =
.
0
11 11 1
() () () () (),
A
py p B pu p y p
−=
0
22 22 2
21
A
py p B pu p y p
up yp
−=
−=
Дополним уравнения регуляризирующим тождеством и запишем
185
полу
1
1
1
0
22
2
2
0 ()
()
()
0()()0
()
()
00
()
0
00 0
()
()
mm
s
Bp
yp
yp
Ap Bp
yp
yp
II
up
I
up
up
−
ченную систему уравнений в виде блочно-матричного обобщенного
уравнения линейной системы
1
() 0Ap
0
⎡
⎤
⎤
⎡⎤
⎡
⎢
⎥
⎢⎥
⎢⎥
−
⎢
⎥
⎢⎥
⎢⎥
=
⎢
⎥
⎢⎥
⎢⎥
−
⎢
⎥
⎢⎥
⎢⎥
⎣⎦
⎣⎦
⎣
⎦
. (6.2.4)
Отсюда видно, что проматрица последовательного соединения двух
дина
0
мических систем, заданных операторными уравнениями в форме левой
факторизации, имеет вид
11
22
() 0 0 ()
0()()0
()
0
00 0
mm
s
A
pB
Ap Bp
p
II
I
×
−
⎡⎤
⎢⎥
−
⎢⎥
Ω=
⎢⎥
−
⎢⎥
⎣⎦
p
. (6.2.5)
Можно сформировать проматрицу с упрощенной структурой. Так, если
перв
й сис
11
0
22 2
) () ()
() () 0 () ()
0 0 () ()
s
ое уравнение взаимосвязи учитывать как новое обозначение входных
сигналов второй подсистемы
2
()up
, то вместо формулы (6.2.4) получим
обобщенное уравнение линейно темы
11
() 0 (
0
A
pBpypyp
B
pAp yp yp
I
up up
⎡
⎤
⎤⎡⎤
−
⎡
⎢
⎥
⎢⎥
⎢⎥
−=
⎢
⎥
⎢⎥
⎢⎥
⎢
⎥
⎢⎥⎢⎥
⎣⎦⎣⎦
⎣
⎦
,
в соответствии с которым проматрица последовательного соединения двух
1
) 0 ()
() () () 0
00
s
подсистем определяется тождеством
1
(
A
22
pBp
pBpAp
I
×
−
⎡⎤
⎢⎥
′
Ω=−
⎢⎥
⎢⎥
⎣⎦
. (6.2.6)
Встречно-параллельное соединение (рис.6.2.3). При встречно-параллельном
Рис.6.2.3. подсистем
соединении подсистем первая подсистема стоит в прямой цепи, а вторая – в
обратной цепи.
Структура встречно-параллельного соединения двух
186
