Асанов А.З. Введение в математическое моделирование динамических систем
Подождите немного. Документ загружается.

управляемой КФ (другие названия: строчно-сопровождающая КФ, КФ
фазовых переменных и др.). Такое название обусловлено тем, что КФ (5.9.11)
управляема при любых значениях коэффициентов передаточной функции.
Наблюдаемость системы (5.9.11) не гарантируется, она зависит от свойств
пары матриц A и C.
Если исходная система задана произвольной тройкой матриц A,B,C,
то переход к канонической форме
(5.9.11) возможен различными способами.
Необходимым и достаточным условием существования перехода от
произвольного описания в пространстве состояний к строчной управляемой
КФ (5.9.11) является управляемость пары (A,B), где A,B – матрицы в
исходном описании.
Наиболее простой метод перехода к КФ (5.9.11) – метод передаточной
функции. Он основан на вычислении передаточной функции исходной
системы
(
)
1
W( p) C pI A B
−
=−
с последующим использованием формул
(5.9.10) и (5.9.11).
Другой метод перехода от произвольной формы описания динамической
системы в пространстве состояний к строчной управляемой фробениусовой
канонической форме основывается на использовании преобразующей
матрицы Т согласно формулам (5.9.7). В данном случае
1
ст нов
TRR
−
=
. Здесь
– матрица управляемости исходной ("старой") системы, а
ст
R
1
нов
R
−
–
обращенная матрица управляемости ("новой") строчно-управляемой
канонической формы. Исходя из (5.9.11), нетрудно установить, что
12 1
23
1
1
... 1
... 1 0
... ... ... ... ...
1... 0 0
10...00
n
нов
n
R
αα α
αα
α
−
−
−
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
=
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
Элементы
i
α
– коэффициенты характеристического полинома исходной
динамической системы
1
11
nn
n
det( pI A ) p p ... p
0
α
αα
−
−
−
=+ +++
.
Другие методы перехода не столь очевидны, требуют нахождения
специальных матричных форм – матриц управляемости, матриц Вандер-
монда и т.д., и здесь не приводятся.
167
Строчная наблюдаемая КФ
Эта каноническая форма имеет в своем описании матрицы
1
2
1
012 1
010 0
1
001 0
0
000 1
0
0
T
n
nn
... b
... b
A ... ... ... ... ... , B ... , C
...
... b
... b
ααα α
−
−
⎡⎤⎡⎤
⎡⎤
⎢⎥⎢⎥
⎢⎥
⎢⎥⎢⎥
⎢⎥
⎢⎥⎢⎥
⎢⎥
==
⎢⎥⎢⎥
⎢⎥
⎢⎥⎢⎥
⎢⎥
⎢⎥⎢⎥
⎢⎥
−−− −
⎣⎦
⎣⎦⎣⎦
=
. (5.9.12)
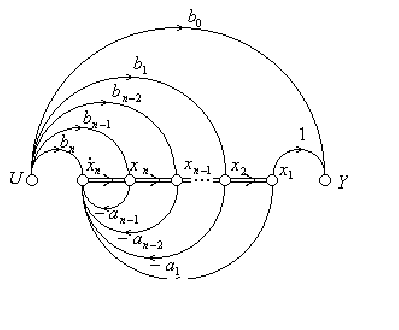
Граф строчной наблюдаемой КФ приведен на рис. 5.9.7.
Рис. 5.9.7. Граф строчной наблюдаемой КФ
Переход от произвольной передаточ-
ной функции (2.67) к строчной наблюю-
даемой КФ заключается в совершенно
тривиальном определении элементов
матриц A и C и в вычислении элементов
матрицы B с помощью следующего
соотношения
10
12 1
21
23
12
1
1
1
10
100
10 00
n
nn
n
nn
b
...
b
...
... ...
... ... ... ... ...
b
...
b
...
β
αα α
β
αα
β
α
β
−
−−
−
−
⎡
⎤⎡ ⎤
⎡⎤
⎢
⎥⎢ ⎥
⎢⎥
⎢
⎥⎢ ⎥
⎢⎥
⎢
⎥⎢ ⎥
⎢⎥
=
⎢
⎥⎢ ⎥
⎢⎥
⎢
⎥⎢ ⎥
⎢⎥
⎢
⎥⎢ ⎥
⎢⎥
⎣⎦
⎣
⎦⎣ ⎦
. (5.9.13)
Характерной особенностью этой КФ является то, что так называемая
матрица наблюдаемости системы в этом случае имеет вид
1
100 0
010 0
001 0
000 1
TTT TnT
нов нов нов нов нов нов
...
...
QCAC...(A)C
...
... ... ... ... ...
...
−
⎡
⎤
⎢
⎥
⎢
⎥
⎡⎤
⎢
⎥
==
⎣⎦
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
.
т.е. является единичной и ее ранг всегда равен n. Отсюда делаем вывод о
том, что
такая КФ всегда наблюдаема (управляемость не гарантируется).
Учитывая это, а также вид матрицы A, данная КФ называется строчной
наблюдаемой КФ.
Необходимым и достаточным условием существования перехода от
168

произвольного описания в пространстве состояний к строчной наблюдаемой
КФ (2.70) является наблюдаемость пары (
A
, ), где C
A
, – матрицы в
исходном описании.
C
Переход к строчной наблюдаемой КФ от произвольной наблюдаемой
системы может быть осуществлен с помощью преобразующей матрицы
по формулам
1
()
Т
TQ
−
=
111ТТ Т T
нов ст ст нов ст ст нов ст ст
1
A
T AT QA(Q), B T B QB, C CT C(Q)
−−−
== == ==
−
. (5.9.14)
Проиллюстрируем приведенные методы получения строчной
наблюдаемой КФ на примерах.
Пример 1.
Исходная система описывается передаточной функцией
2
1
()
32
Wp
pp
=
+
+
В этом случае матрицы
и определяются легко
нов
A
нов
C
01
23
A
⎡
⎤
=
⎢
⎥
−
−
⎣
⎦
,
[
]
01
=
C .
Для определения матрицы
воспользуемся соотношением (5.9.13 )
нов
B
1
2
31 1
10 0
b
b
⎡⎤
⎡
⎤⎡
=
⎢⎥
⎤
⎢
⎥⎢⎥
⎣
⎦⎣
⎣⎦
⎦
, откуда
1
0
2
1
=
=
b
b
, т.е. .
⎥
⎦
⎤
⎢
⎣
⎡
=
1
0
нов
B
Пример 2. Исходная система описывается в пространстве состояний уравнениями,
содержащими следующие матрицы
26
25
A
⎡⎤
=
⎢
−−
⎣⎦
⎥
, ,
⎥
⎦
⎤
⎢
⎣
⎡
−
=
1
1
B
[
]
11
=
C .
Описание этой же системы в строчной наблюдаемой канонической форме возможно,
т.к. матрица наблюдаемости
имеет ранг, равный 2, т.е. система
наблюдаема.
[]
⎥
⎦
⎤
⎢
⎣
⎡
==
11
01
TTT
CACQ
Преобразующая матрица
, a .
⎥
⎦
⎤
⎢
⎣
⎡
−
==
−
11
10
)(
1 T
QT
⎥
⎦
⎤
⎢
⎣
⎡
=
10
11
T
Q
Тогда по формулам (5.9.14)
1
01
()
23
TT
нов
AQAQ
−
⎡
⎤
==
⎢
⎥
−
−
⎣
⎦
, , .
⎥
⎦
⎤
⎢
⎣
⎡
==
1
0
BQB
T
нов
[]
01=
нов
C
Для проверки определим матрицу наблюдаемости полученной канонической формы
10
01
ТТТ
нов нов нов нов
QCАС E
⎡⎤
⎡⎤
==
⎢⎥
⎣⎦
⎣⎦
=
, rank Q=2, система наблюдаема.
169
В заключение отметим, что существуют и другие фробениусовы
канонические формы (столбцовая управляемая КФ, столбцовая наблюдаемая
КФ и др.). Общей чертой рассмотренных и нерассмотренных здесь
канонических форм является фробениусова (сопровождающая) структура
матрицы A, в которой все варьируемые элементы матрицы расположены в
последней строке или последнем столбце. Значения этих элементов во всех
случаях совпадают
с точностью до знака с коэффициентами
характеристического полинома системы.
Кроме этого, в каждой КФ одна из матриц В или С имеет максимально
простой вид (один элемент единичный, остальные – нулевые); элементы
другой матрицы могут принимать различные значения.
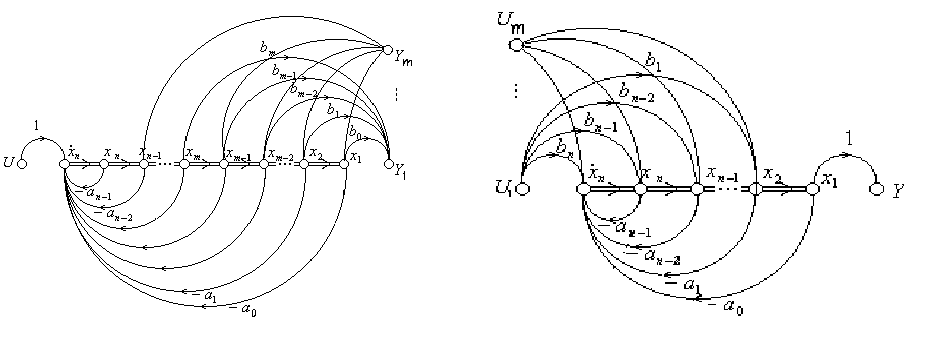
Управляемые КФ допускают очевидное обобщение на системы с одним
входом и произвольным числом выходов (
рис. 5.9.8), а наблюдаемые КФ
обобщаются на системы с произвольным числом входов и одним выходом
(рис. 5.9.9).
Рис. 5.9.8. Граф управляемой КФ Рис. 5.9.9. Граф наблюдаемой КФ
системы с одним входом и
m выходами системы с m входами и одним выходом
5.9.2. Жорданова (параллельная) каноническая форма
Суть параллельной КФ состоит в разложении исходной системы на
независимые параллельные подсистемы. При этом сумма порядков
подсистем равняется общему порядку системы, а такое представление в
целом удобно для анализа динамики системы и исследования ее свойств.
170
Для получения параллельной КФ передаточную функцию системы
представляют в виде суммы простейших дробей, каждую из которых
реализуют с помощью отдельной схемы. Если корни знаменателя
передаточной функции вещественны и различны, то возможно разложение
вида
1
110
1
110
n
n
nn
n
p
... p
W( p)
p
p ... p
βββ
α
αα
−
−
−
−
++ +
==
++++
, (5.9.15)
где С
1
, С
2
,..., С
n
– постоян-
ные коэффициенты, которые
можно найти приведя
правую часть равенства к
общему множителю и
приравнивая коэффициенты
числителей при соответствующих степенях переменной в левой и правой
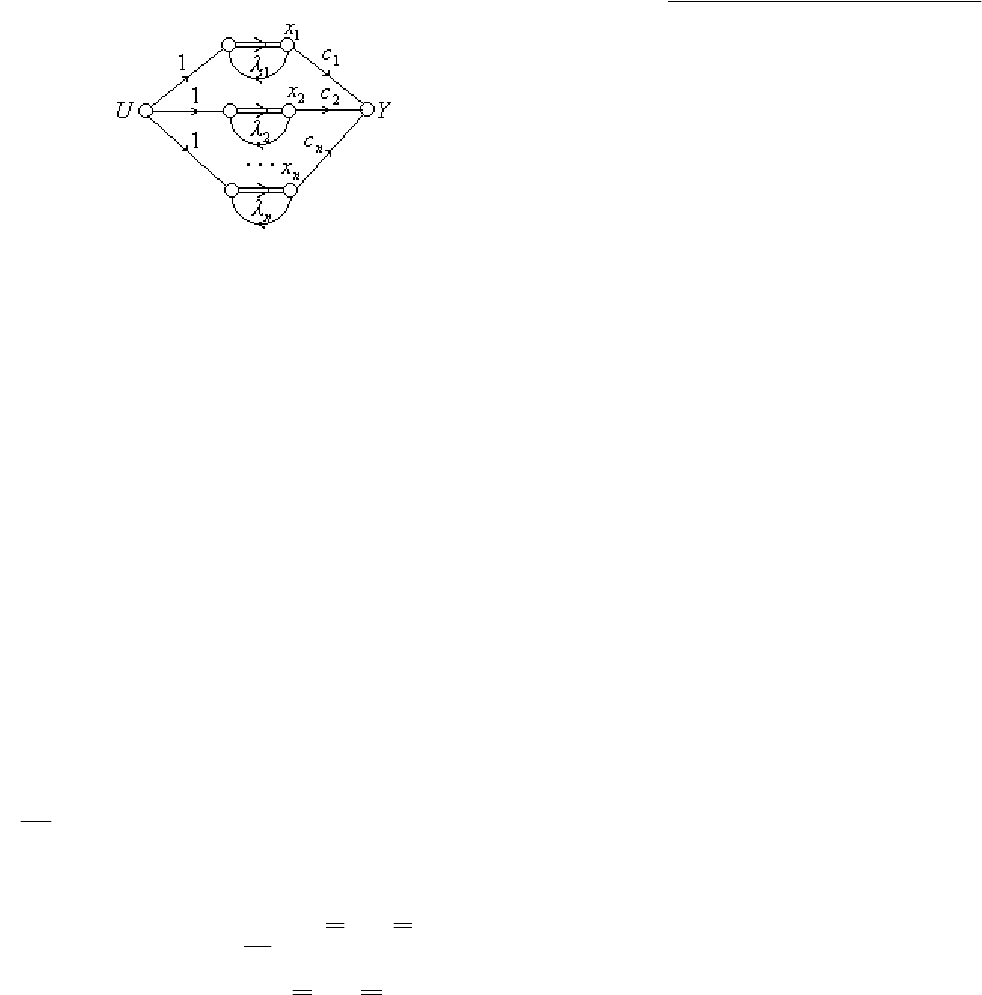
частях равенства. Легко увидеть, что реализации передаточной функции
соответствует параллельная структура, изображенная на рис. 5.9.10.
Рис. 5.9.10. Граф параллельной КФ системы (5.9.16)
Отметим, что существование и единственность параллельной КФ
определяется единственностью представления любой
дробно-рациональной
передаточной функции в виде суммы простейших дробей.
Описание параллельной КФ в пространстве состояний может быть
легко получено из графа системы на рис. 5.9.10.
111
11 2 2 nn
nnn
xxU,
................... Y c x c x ... c x ,
xxU,
λ
λ
=+
⎧
⎪
=+ ++
⎨
⎪
=+
⎩
(5.9.16)
где
i
λ
– корни характеристического уравнения динамической системы,
1i,= n, – постоянные коэффициенты.
i
c
В матричной записи это описание имеет вид
d
XAXBU
dt
YCXDU,
=+
=+
,
(5.9.17)
где
171

1
2
0 ... 0
0 ... 0
... ... ... ...
0 0 ...
n
A
λ
λ
λ
⎡⎤
⎢⎥
⎢⎥
⎥
=
⎢
⎢⎥
⎣⎦
,
1
1
...
1
B
⎡⎤
⎢⎥
⎢⎥
=
⎢⎥
⎢⎥
⎣⎦
,
[]
12
...
n
CCC C= ,
[]
0D = .
Отсюда видно, что характерным признаком описания параллельной КФ в
пространстве состояния является диагональность матрицы
A
: по главной
диагонали матрицы располагаются собственные числа матрицы (или по
другому, корни характеристического полинома системы).
Уже отмечалось нами, что для приведения матрицы A к диагональному
виду необходимо в качестве координатных осей в пространстве состояний
использовать базис, состоящий из собственных векторов этой матрицы. По
этой причине параллельную КФ называют также жордановой
КФ.
Следовательно, для перехода от произвольного описания системы в
пространстве состояний к параллельной КФ необходимо отыскание
собственных векторов
исходной матрицы
12 n
t , t , ..., t
A
и выполнение
преобразования подобия по формулам
11
A
TAT, B TB, C CT
−−
===
, где
[
]
12 n
Ttt...t
=
. (5.9.18)
Здесь особо отметим то обстоятельство, что процедура перехода к
параллельной КФ не обусловлена никакими условиями управляемости или
наблюдаемости исходной системы, как это было ранее при переходе к
фробениусовым КФ.
Пример.
Динамическая система задана в пространстве состояния уравнениями
1123
2123
3123
12 3
42
22
2
22
2
x
xx xU
x
xx x U
x
xxx U
Yxx x
=− + + +
=− − + +
=− + − +
=−+
Матрицы данного исходного описания имеют вид
[]
41 2 1
212 2 212
11 1 2
A,B,C
−
⎡⎤ ⎡⎤
⎢⎥ ⎢⎥
=− − = = −
⎢⎥ ⎢⎥
⎢⎥ ⎢⎥
−−
⎣⎦ ⎣⎦
.
Требуется найти параллельную КФ данной системы.
Решение. Характеристическое уравнение имеет вид
172

41 2
det( ) 2 1 2 ( 1) ( 2) ( 3) 0
111
EA
λ
λλλλλ
λ
+−−
⎡⎤
⎢⎥
−=− + − =+ + +=
⎢⎥
⎢⎥
−+
⎣⎦
.
Корни характеристического уравнения системы или, что равнозначно, собственные
числа матрицы
A:
12
12,,
3
3
λ
λλ
=− =− =−
.
Собственные векторы получаем, решая уравнения
111 2 22 3 3
,,
3
A
tt At t At t
λ
λλ
=
==
и выбирая три линейно-независимых решения
t,
. Тогда
T,
12 3
11
10
11
1
1
0
t ,t
⎡⎤ ⎡⎤ ⎡⎤
⎢⎥ ⎢⎥ ⎢⎥
== =
⎢⎥ ⎢⎥ ⎢⎥
⎢⎥ ⎢⎥ ⎢⎥
⎣⎦ ⎣⎦ ⎣⎦
T
−
−
1
111 1 1 1
101 1 10
110 1 0 1
⎡
⎤⎡⎤
⎢
⎥⎢⎥
==−
⎢
⎥⎢⎥
⎢
⎥⎢⎥
⎣
⎦⎣⎦
.
Для получения параллельной КФ осуществим замену переменных
Х=ТZ. Тогда по
формуле (2.74) имеем
[]
11
10 0 3
020, 1, 34
00 3 1
ATAT BTB C
−−
−
⎡⎤ ⎡⎤
⎢⎥ ⎢⎥
==− ==− =
⎢⎥ ⎢⎥
⎢⎥ ⎢⎥
−−
⎣⎦ ⎣⎦
1
.
Рис. 5.9.11 иллюстрирует структуры исходной и результирующей систем.
Рис. 5.9.11. а) Граф исходной системы; б) Граф параллельной КФ
В случае, если в исходной системе имеются кратные собственные числа
матрицы A (или иначе говоря, кратные корни характеристического
полинома), форма записи параллельной КФ системы усложняется.
Так, пусть имеется корень
1
λ
кратности k. Тогда разложение
передаточной функции на простейшие дроби принимает вид
1
110
11
12 1
1
11 1 1
n
n
k
kn
kk
kk
kn
p...p
W( p)
(p )(p )...(p )
CC CC C
... ...
(p ) (p ) (p ) (p ) (p )
βββ
λλ λ
n
λ
λλλ
−
−
+
+
−
+
++ +
==
−− −
=+ +++ ++
−− −− −
λ
(5.9.19)
Такому разложению соответствует граф, приведенный на рис.5.9.12.
173
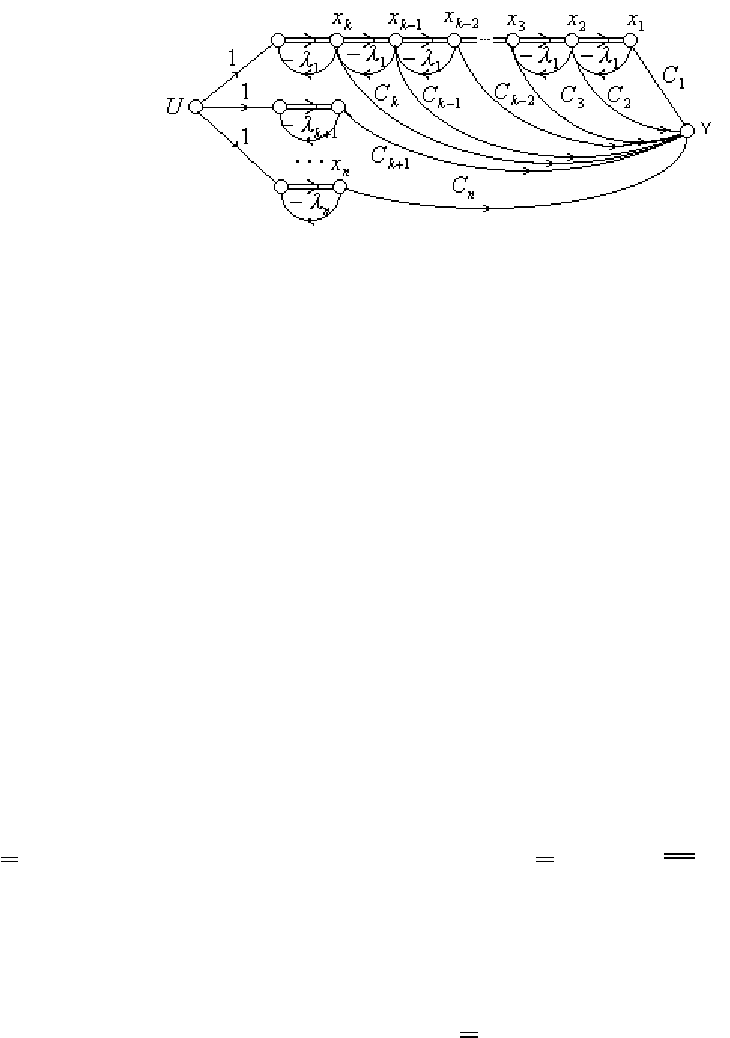
Уравнение состояния системы, при выборе в качестве переменных
состояния выходных сигналов интеграторов, имеют вид
Рис. 5.9.12. Г
р
а
ф
системы
1112
2123
111
1
11
kkk
kk
kkk
xxx
xxx
....................
x
xx
xxU
x
xU
λ
λ
λ
λ
λ
−−
++
=+
⎧
⎪
=+
⎪
⎪
⎪
nnn
......................
xxU
λ
=
+
⎪
⎨
=+
⎪
⎪
=
+
⎪
(5.9.20)
⎪
⎪
=+
⎩
Матрицы
A
, , имеют вид B C
1
2
1
1
10 0000 0
0
0100000
0
000 100 0
0
000 0 00 0
1
000 0000
1
T
n
... ... C
... ...
... ... ... ... ... ... ... ... ... ...
...
A ... ... , B , C
... ...
... ... ... ... ... ... ... ... ... ...
...
... ...
λ
λ
λ
λ
λ
⎡⎤
⎡⎤
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
==
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎣⎦
⎣⎦
1
2
1k
k
n
C
...
C
C
...
C
−
=
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
(5.9.21)
Как видно, полученная матрица
A
уже не является диагональной.
Корню
1
λ
кратности k в ней соответствует матричная клетка
1
A
, размеров
вида kk×
1
1
1
1
1
10 0
01
000 1
000
...
...
A
... ... ... ... ...
...
λ
λ
λ
0
λ
⎡⎤
⎢⎥
⎢⎥
⎢⎥
=
⎢⎥
⎢⎥
⎢⎥
⎣⎦
.
174
Матрицы такого вида (с единицами над главной диагональю)
называются клетками Жордана. Характеристический многочлен клетки
Жордана равен
(
)
1
k
p
λ
−
.
В случае нескольких кратных корней матрица
A
, соответствующая
параллельной КФ, будет иметь так называемую жорданову нормальную
форму
1
2
00
00
000
m
A...
A...
A
... ... ... ....
A
⎡⎤
⎢⎥
⎢
=
⎢
⎢⎥
⎣⎦
⎥
⎥
, где
i
A
– клетки Жордана.
Число клеток равно числу различных корней характеристического
уравнения системы, а размеры их определяются кратностью корней.
При наличии пары комплексных сопряженных корней
12
j
s, js
λ
σλσ
=
+−
.
соответствующие им две простейшие дроби первого порядка в разложении
объединяются в одну дробь второго порядка с вещественными
коэффициентами
12 12
22
12
2
CC CpC
pp pp
λλ σσ
2
s
′
′
+
+=
−− −++
. (5.9.22)
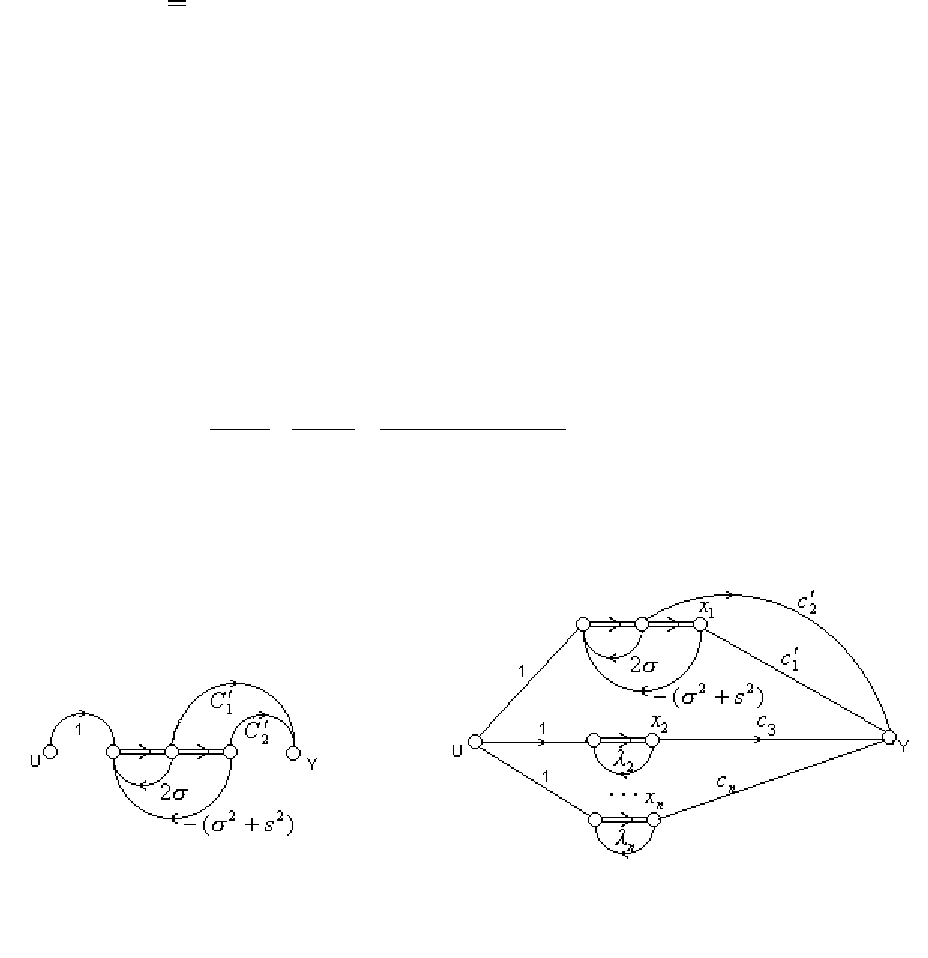
Соответствующая (5.9.22) строчная управляемая реализация этой дроби
имеет вид, представленный на рис. 5.9.13.
Рис.5.9.13. Реализация д
р
оби
(
5.9.22
)
Рис. 5.9.14. Граф параллельной КФ при наличие
двух комплексных корне
й
Граф параллельной КФ при наличии двух комплексных сопряженных
корней представлен на рис. 5.9.14. Нетрудно увидеть, что в матричной записи
175

комплексная клетка Жордана будет выражать фробениусовой формой
1
22
01
2
A
(s)
σ
σ
⎡
=
⎢
−+
⎣⎦
⎤
⎥
(5.9.23)
Таким образом, при наличии пары комплексных корней в жордановой
нормальной форме одна из клеток будет представлять собой матрицу
(5.9.23). В случае кратных комплексных корней клетки Жордана примут
еще более сложный вид.
5.9.3. Последовательная (каскадная) каноническая форма
Исходная динамическая система может быть представлена и в виде
последовательно соединенных подсистем
12 k
W(p) W(p)W( p) ... W (p)=
. (5.9.24)
Такое представление называется последовательной или каскадной КФ
системы. Очевидно, что сумма порядков подсистем равна порядку исходной
системы.
Обычно для получения каскадной КФ передаточную функцию
динамической системы представляют в виде произведения простых
дробей 1-го или 2-го порядка. Каждую из этих дробей реализуют с помощью
отдельной схемы.
Допустим,
i
µ
– нули, а
j
λ
– полюсы передаточной функции .
Если все они вещественны и различны, то возможно разложение следующим
образом:
W( p)
10 1 2
1
110 12
m
m m
m
nn
n n
p
... p ( p )( p )...( p )
W( p)
p
p ... p ( p )( p )...( p )
β
ββ µ µ µ
β
α
αα λ λ λ
−
−
++ + − − −
==
++++ −− −
, (5.9.25)
где
1
11
i
ii
ii
p
W ( p ) , i ,m; W ( p ) , i m ,n
pp
µ
λλ
−
== ==
−−
+
.
Каждая из простых дробей может быть реализована структурами,
представленными на рис. 5.9.15, а реализация самой передаточной
функции (5.9.25) – на рис. 5.9.16.
176
