Асанов А.З. Введение в математическое моделирование динамических систем
Подождите немного. Документ загружается.


Использование свойств преобразования Лапласа и таблицы соответствий «оригинал
– изображение» позволяет получить решение более легким способом. Для этого
представим полученный результат в виде суммы элементарных дробей, воспользовавшись
методом неопределенных коэффициентов.
Пусть полученное изображение представимо в виде
()() ()()
2
3131
23 2 3
p
pABC
pp p p p p
++
=+ +
++ + +
,
где
– неизвестные пока коэффициенты, значения которых необходимо найти
,,ABC
Произведем очевидные алгебраические преобразования дроби
()()
()
(
)
()()
(
)
()()
(
)
()()
()()
2
23 3 2
3131
2 3 23 23 23 23
Ap p Bpp Cpp
AB C p p
pp p ppp pppppp ppp
++ + +
+
+
++= + =
+ + ++ ++ ++ ++
.
Тогда очевидно, что коэффициенты при одинаковых степенях
p
должны равняться:
3
5321
61
ABC
ABC
A
3
+
+=
+
+=
=
,
Эта система алгебраических уравнений имеет решением значения
13
11
,,
62
AB C
1
3
−
== =
.
Таким образом, полученное ранее изображение
может быть представлено в виде
()Yp
()() ()()
2
113 11
3131
63
2
()
23 2
pp
Yp
pp p p p p
++
==+−
3
+
+++
.
Используя свойства преобразования Лапласа и таблицу соответствий, получаем
{}
()() () ()
11 11 1
113 11 1 13 11
636
22
() ( )
23 2
yt L Y p L L L L
pp p p p p
−− −− −
⎧⎫⎧⎫⎧⎫
⎪⎪⎪⎪⎪⎪
==+−=+ −
⎨⎬⎨⎬⎨⎬
++ + +
⎪⎪⎪⎪⎪⎪
⎩⎭⎩⎭⎩⎭
3
3
⎧⎫
⎪⎪
⎨⎬
⎪⎪
⎩⎭
.
Окончательно искомое решение дифференциального уравнения принимает вид
()
23
113 11
() , 0
62 2
tt
yt e e t
−−
=
+− >
.
Решение системы дифференциальных (или интегро-дифференциальных)
уравнений с постоянными коэффициентами производится способом,
аналогичным приведенному выше. Каждое из уравнений, входящих в
систему, преобразуется по Лапласу, а затем получившаяся система
алгебраических уравнений решается относительно изображения решения.
Оригинал определяется указанными выше способами.
3.4.2. Передаточные функции и операции с ними
Рассмотрим линейную динамическую систему с постоянными
параметрами, т.е. параметрами, не зависящими ни от времени, ни от
состояния системы.
117

Пусть динамическая система описывается дифференциальным
уравнением
1
110 1
(n) (n ) (m)
nn m
a y (t) a y (t) ... ay(t) a y(t) b u (t) ... bu(t) bu(t
0
)
−
−
′′
++++=+++
(3.4.1)
в предположении, что
– выходная переменная,
()yyt= ()uut
=
– входная
переменная,
при и что система при
() 0ut ≡
0t < 0t
=
находилась в нулевых
начальных условиях
const, 1,
i
ain==,
const, 1,
j
m==
0
)()
bj
.
Преобразуем последнее уравнение по Лапласу, учитывая нулевые
начальные условия и свойства преобразования Лапласа
1
-1 1 0
1
11
() () ... () ()
() () ... () ()
nn
nn
mm
mm
asYs a s Ys asYs aYs
bsUs b s Us bsUs bUs
−
−
−
++++=
=+ +++
(3.4.2)
или
11
-1 1 0 1 1 0
(...)()( ...
nn m m
nn m m
as a s as a Y s bs b s bs b U s
−−
−
++++ =+ +++
,
где
{
}
() ()Ys Lyt=
– изображение выходной переменной (сигнала),
{
}
() ()Us Lut=
– изображение входной переменной (сигнала).
Передаточная функция системы
определяется как отношение
изображений по Лапласу выходного
и выходного сигналов при
нулевых начальных условиях
()Ws
()Us ()Ys
1
11
1
11
mm
mm
nn
nn-
Y( s ) b s b s ... b s b
W(s)
U( s ) a s a s ... a s a
−
−
−
0
0
+
++ +
==
+
++ +
, (3.4.3)
где
– изображение по Лапласу от функции ,
– изображение по Лапласу от функции .
{}
0
() () ()
st
Ys Lyt yte dt
∞
−
==
∫
()yt
{}
0
() () ()
st
Us Lut ute dt
∞
−
==
∫
()ut
Передаточная функция
характеризует динамические свойства
системы, это функция не зависит от воздействия, приложенного к системе, а
зависит только от параметров системы.
()Ws
Представим исходное дифференциальное уравнение (3.4.1) в
операторной форме
11
-1 1 0 1 1 0
( ... ) ( ) ( ... ) ( )
nn m m
nn mm
ap a p ap a yt bp b p bp b ut
−−
−
++++=+ +++
, (3.4.4)
или
()() ()()
A
pyt Bput
=
,
118

где
d
p
dt
=
– оператор дифференцирования, а
()
A
p
и
()
B
p
– полиномы:
1
-1 1 0
() ...
nn
nn
A
papap apa
−
=+ +++
,
1
11
() ...
mm
mm
Bp bp b p bp b
−
− 0
=
++++
.
Анализируя уравнения (3.4.1) и (3.4.4), нетрудно установить, что при
нулевых начальных условиях комплексная переменная
s
может быть
отождествлена с оператором дифференцирования
p
. Тогда чисто формально
передаточная функция может быть получена как отношение двух полиномов
относительно оператора дифференцирования
1
11
1
11
mm
mm
nn
nn-
0
0
B
( p ) b p b p ... b p b
W( p)
A
( p ) a p a p ... a p a
−
−
−
+
++ +
==
+
++ +
. (3.4.5)
Далее будем использовать обозначение
p
, полагая по контексту за этим обозначением
или оператор дифференцирования, или комплексную переменную.
Из определения передаточной функции следует, что
Y( p) W( p)U(p)
=
, (3.4.6)
т.е. зная передаточную функцию
и определив изображение
воздействия
на систему, можно найти изображение реакции
системы. Тогда, осуществив переход от изображения
к оригиналу ,
можно получить описание процесса изменения выходной координаты
системы при приложении к этой системе входного воздействия
.
()Wp ()Up
()ut ()Yp
()Yp ()yt
()ut
Если начальные условия ненулевые, то вместо уравнения (3.4.6) получим
уравнение
н
Y( p) W(p)U( p) V (p)
=
+
,
где
– слагаемая, учитывающая ненулевые начальные условия.
()
н
Vp
Пример. Пусть динамическая система описывается дифференциальным уравнением
() 5 () 6 () 1yt yt yt
′′ ′
++=
при
(0) 2y
=
,
(0) 3y
′
=−
.
Тогда, учитывая свойства преобразования Лапласа, можно записать
{
}
() ()Up Lut= , ,
{
}
() ()Yp Lyt=
{
}
() ( ) (0) ( ) 2Lyt pYp y pYp
′
=−=−,
{
}
22
() () (0) (0) () 2 3Lyt pYp py y pYp p
′′ ′
=
−−= −+.
Тогда изображение исходного уравнения приобретает вид
()
(
)
2
() 2 3 5 () 2 6() ()
p
Yp p pYp Yp Up−++ −+ =
или
2
() 5 () 6() () 2 7pYp pYp Yp Up p
+
+=++
,
22
12
() ()
56 56
p
Yp Up
pp pp
7
+
=+
+
+++
.
119
Таким образом, в данном случае
2
1
()
56
Wp
pp
=
+
+
,
2
27
()
56
н
p
Vp
pp
+
=
+
+
.
Введение передаточных функций позволяет решать многие задачи
анализа и синтеза динамических систем операторными методами.
Основным достоинством передаточных функций является возможность
достаточно легко и просто описать систему, когда известны передаточные
функции подсистем (элементов) и схемы соединения подсистем друг с
другом.
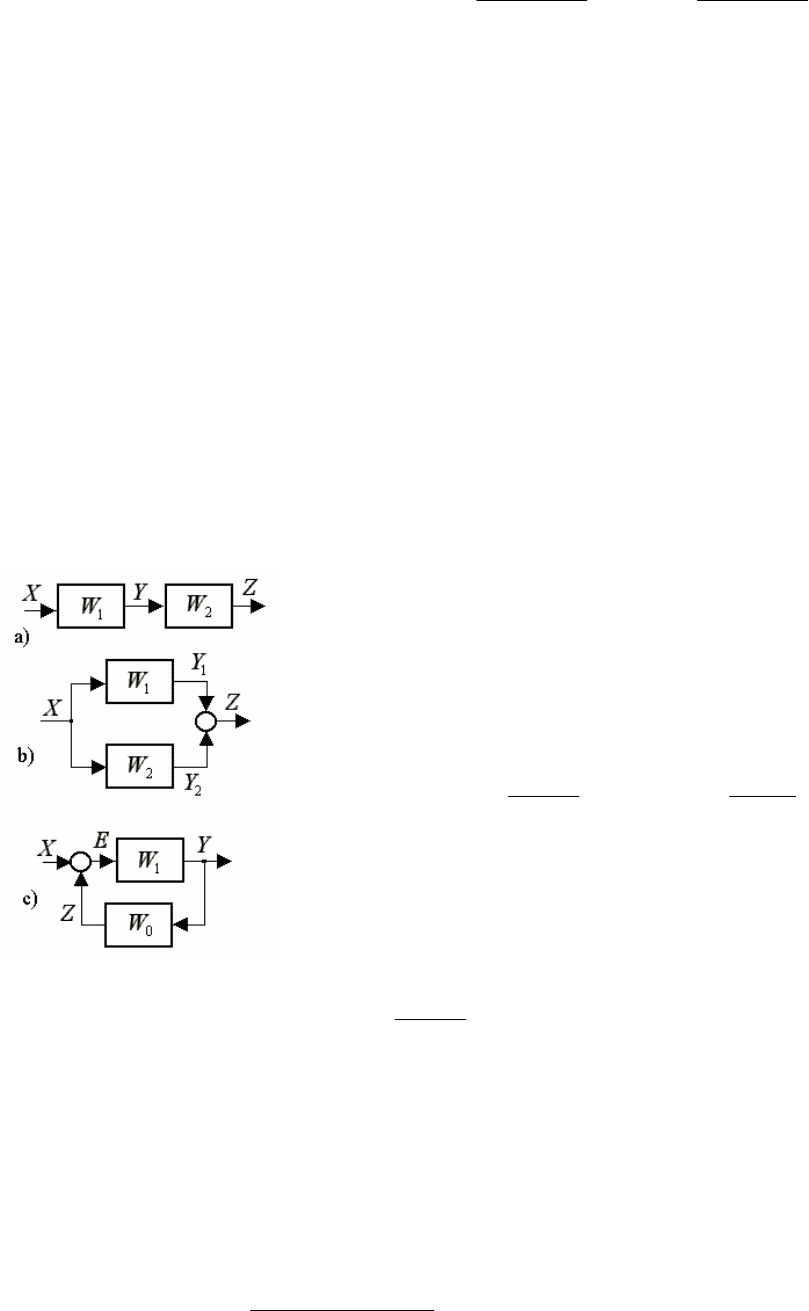
Известно, что существует три вида типовых соединений подсистем друг
с другом –
последовательное (рис.3.4.2а), параллельное (рис.3.4.2b) и соеди-
нение с обратной связью (встречно-параллельное) (рис.3.4.2с). Возникают
значительные трудности при определении математической модели всего
соединения, когда математические модели подсистем заданы в
дифференциальной форме.
При использовании моделей в форме
передаточных функций эта процедура значительно
облегчается и формализуется. Так, для
последовательного соединения видно, что
с учетом
определения (3.4.1) получается
12
p) Z(p)
, W(p)
p) Y(p)
==
Y(
W(p)
X(
1
Y( p) W( p)X( p)=
.
Тогда
,
2
,
Z(p) W (p)Y(p)
=
.
Отсюда
21
Z
(p) W(p)W(p)X(p)
=
,
21 12
Z( p )
W(p) W(p)W(p) W(p)W ( p)
X( p)
== =
. Таким
образом, последовательному соединению подсистем соответствует умно-
жение передаточных функций.
Рис. 3.4.2. Типовые
соединения
Рассуждая аналогично, можно получить, что параллельному соединению
подсистем соответствует сложение передаточных функций, т.е.
, встречно-параллельному соединению соответствует
соотношение
12
W( p) W( p) W ( p)=+
1
01
1
W(p)
W( p)
W(p)W(p)
=
−
для случая
E
XZ
=
+ , и соотношение
120

1
01
1
W(p)
W( p)
W(p)W(p)
=
+
для случая
E
XZ
=
− .
Проведение арифметических операций над дробно-рациональными
полиномами (передаточными функциями) значительно проще, чем получение
аналогичного по сути результата при использовании дифференциальных
уравнений подсистем.
3.4.3. Связь передаточной функции с другими характеристиками
Применение преобразования Лапласа к дифференциальному уравнению
1
110 1
(n) (n ) (m)
nn m
a y ( t ) a y ( t ) ... a y ( t ) a y( t ) b u ( t ) ... b u ( t ) b u( t
0
)
−
−
′′
++++=+++
в предположении, что
()yyt
=
– выходная переменная, – входная
переменная,
при
()uut=
() 0ut ≡
0t
<
и что система при 0t
=
находилась в нулевых
начальных условиях, даёт
11
-1 1 0 1 1 0
( ... ) ( ) ( ... ) ( )
nn m m
nn mm
ap a p ap a Y p bp b p bp b U p
−−
−
++++ =+ +++
Отсюда по определению передаточной функции имеем:
1
11
1
11
mm
mm
nn
nn-
Y( p ) b p b p ... b p b
W( p)
U( p ) a p a p ... a p a
−
−
−
0
0
+
++ +
==
+
++ +
(3.4.7)
и другое соотношение
() () ()Yp WpUp
=
, где – изображение выходной
переменной (сигнала),
– изображение входной переменной (сигнала).
()Yp
()Up
В дальнейшем будем предполагать выполнение условия
, которое
справедливо для физически реализуемых систем. При этом рациональная
дробь
mn<
()
()
()
B
p
Wp
A
p
=
является правильной и в соответствующей ей весовой
функции
отсутствуют слагаемые типа дельта-функции.
()wt
Полином
()
A
p
, стоящий в знаменателе дробно-рациональной
передаточной функции (3.4.7), называется характеристическим полиномом
системы, а его корни
12
, , ...,
n
λ
λλ
– полюсами передаточной функции .
Корни
()Wp
12
, ,...,
m
µ
µµ
полинома
()
B
p
называются нулями передаточной функции.
Допустим
, тогда
() 1()Ut t=
1
()
Up
p
=
. В этом случае:
1
() ()
Yp Wp
p
=
–
изображение реакции системы на единичный ступенчатый сигнал.
121

-1
1
() () ( )
yt ht L W p
p
⎧⎫
==
⎨⎬
⎩⎭
,
{
11
1
() ( ) ( )
ht L p Wp L Wp
p
−−
⎧⎫
′
==
⎨⎬
⎩⎭
}
. Таким
образом,
{}
0
pt
dh
W( p) L h(t ) e dt
dt
∞
−
′
==
∫
. Попутно получается, что
()
()
dh t
wt
dt
=
,
– весовая (импульсная) характеристика.
()wt
Допустим
() ()ut t
δ
=
, тогда
() 1Up
=
,
() 1 ()Yp Wp
=
⋅
.
{
}
{
}
11
() ( ) ( ) ()yt L Y p L W p wt
−−
== =
, т.е. .
Передаточная функция
является изображением весовой функции
, и наоборот, весовая функция является функцией-оригиналом
передаточной функции.
{}
0
pt
W( p) L w(t) w(t)e dt
∞
−
==
∫
()Wp
()wt ()wt
Имея передаточную функцию системы, достаточно легко получить
амплитудно-фазовую частотную функцию
(Wj)
ω
этой системы. Из
сравнения формул-определений этих характеристик видно, что для этого
формально достаточно в выражении передаточной функции заменить
p
на
j
ω
:
(
)
(
)
(
)
() () ()
1
11
1
11
mm
mm
nn
pj
nn
b j b j ... b j b
W( j ) W( p)
aj a j ...aj a
ω
ωω ω
ω
ωω ω
−
−
−
=
−
0
0
+
++ +
==
+
++ +
.
Передаточная функция системы полностью характеризует динамические
свойства линейной динамической системы и поэтому является важнейшей ее
характеристикой.
122
4. Основные формы математических моделей
матричных динамических систем
Современный этап развития теории систем характеризуется тем, что
центральное место в теоретических и прикладных исследованиях занимают
системы со многими входами и выходами. В литературе для таких систем
используются термины "матричные системы", "многомерные системы",
"многосвязные системы", а в англоязычной литературе – MIMO-системы
(Multi-Input Multi-Output).
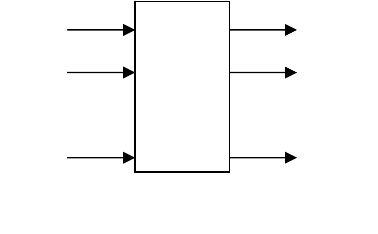
Введенные в предыдущем разделе
понятия и характеристики скалярных систем
могут
быть обобщены на случай с
несколькими входам и выходами (рис.4.0.1).
Вместе с тем, следует отметить, что
матричные системы отличаются от
скалярных не только внешними
(количественными) признаками. Гораздо более важным является то, что для
матричных систем характерны принципиально новые свойства и черты. В
число таких качественно новых свойств можно отнести, например
, свойства
управляемости, наблюдаемости и многое другое.
…
U
m
(t)
U
2
(t)
U
1
(t)
…
Y
k
(t)
Y
2
(t)
Y
1
(t)
S
Рис. 4.0.1 Матричная система
4.1. Матричные передаточная и весовая функции
Рассмотрим матричную динамическую систему S с m входами
и k выходами (рис.4.0.1). Для обозначения входных и
выходных сигналов можно также использовать векторные обозначения
,
и их изображения по Лапласу
U(
,
Y(
.
12 m
u ,u ,...,u
12 k
y ,y ,..., y
u( t )
y( t ) p) p)
Если система S линейна и стационарна, то связь между изображениями
ее входных и выходных сигналов при нулевых начальных условиях может
быть описана о помощью матричной передаточной функции (МПФ )
W(
:
p)
Y( p) W( p)U(p)
=
. (4.1.1)
Элементами матрицы
W(
является скалярные передаточные функции
, характеризующие комплексные коэффициенты передачи от j-го
входа системы до ее i-го выхода:
p)
ij
W(p)
123
11 12 1
21 22 2
12
m
m
kk km
W (p) W (p) ... W (p)
W ( p) W ( p) ... W ( p)
W( p)
... ... ... ...
W ( p) W ( p) ... W ( p)
⎛⎞
⎜⎟
⎜⎟
=
⎜⎟
⎜⎟
⎝⎠
. (4.1.2)
Если система
S конечномерна и физически реализуема, то скалярные
ПФ
являются правильными рациональными дробями, причем для
физически реализуемых систем степень числителя должна быть меньше
степени знаменателя.
ij
W(p)
Соотношение (4.1.1) описывает связь между входом и выходом системы
в операторной форме. Связь между входными и выходными сигналами во
временной области задается векторным интегралом свертки
0
y( t ) w( t )U( )d
τ
ττ
∞
=−
∫
,
который получается применением обратного преобразования Лапласа к
обеим частям соотношения (4.1.1).
Входящая в эту формулу матрица
является оригиналом матрицы
и называется матричной весовой функцией системы. Она, как и
матричная ПФ, полностью описывает многомерную линейную стационарную
систему. Элементами этой матрицы являются скалярные весовые функции
, каждая из которых представляет собой сигнал на i -м выходе системы
при подаче на его
j -й вход импульсного воздействия
w( t )
W( p)
ij
w(t)
j
u(t) (t)
δ
=
:
11 12 1
21 22 2
12
m
m
kk km
w ( t ) w ( t ) ... w ( t )
w (t) w (t) ... w (t)
w( t )
... ... ... ...
w (t) w (t) ... w (t)
⎛⎞
⎜⎟
⎜⎟
=
⎜⎟
⎜⎟
⎝⎠
. (4.1.3)
Если система
S устойчива и физически реализуема, то с течением
времени все компоненты
экспоненциально стремятся к нулю.
w( t )
4.2. Полиномиально-матричное описание динамических
систем
Одним из недостатков описания с помощью матричной весовой и
матричной передаточной функций является сложность перехода от них к
124

структурной реализации в моделях. По этим функциям нелегко даже
определить порядок системы. В этом отношении более удобным является
описание многомерных объектов с помощью системы дифференциальных
уравнений, связывающих входные и выходные сигналы объекта и их
производные. Стандартная форма такого описания для системы S (рис.4.0.1)
имеет вид
11 11
1
iissiirr
a ( p )y ... a ( p )y b ( p )u ... b ( p )u , i ,s++ = ++ = , (4.2.1)
где
p
– оператор дифференцирования, , – операторные
полиномы.
ij
a(p)
ij
b(p)
Число s дифференциальных уравнений (4.2.1.) совпадает с числом
неизвестных
12
s
y ,y ,...,y
, степени операторных полиномов зависят от
структуры и размерности объекта.
Соотношения (4.2.1) удобно записать в полиномиально-матричной форме
A
(p)y(t) B(p)u(t)
=
(4.2.2)
где
A
(p)
,
B
(p)
– полиномиальные матрицы, – векторы
соответствующих размеров.
(), ()yt ut
Пусть через
12
s
n ,n ,...,n
обозначены порядки отдельных
дифференциальных уравнений системы (4.2.1), а через
n – общий порядок
всей системы. Порядок
определяется наивысшей из степеней полиномов
, входящих в i-е уравнение, а общий порядок n равен степени
характеристического полинома системы
i
n
ij
a(p)
0
n
n
A
(p) a p ... a
=
++
,
0
0a
≠
.
Отметим, что определенный таким образом порядок системы (4.2.1)
n в
общем случае не совпадает с суммой порядков
отдельных уравнений
системы, а удовлетворяет неравенству
i
n
1
s
n n ... n
≤
++
.
Путем эквивалентных преобразований системы (4.2.1) (добавляя к
отдельным уравнениям другие, домноженные на произвольные операторные
полиномы) можно привести систему к так называемой правильной строчной
форме, когда приведенное неравенство обращается в равенство.
Целые числа
12
s
n ,n ,...,n
, характеризующие порядки отдельных
уравнений правильной формы, называются структурными показателями
наблюдаемости и играют важную роль в теории многомерных систем.
Существует второй вариант полиномиально-матричного описания,
дуальный по отношению к рассмотренному. Он имеет вид
125
A
(p)z u, y B(p)z==
. (4.2.3)
Первое из этих соотношений представляет собой систему линейных
дифференциальных уравнений для определения компонент
1
s
z ,...,z
вектора
вспомогательных переменных z, при этом в правые части этих уравнений не
входят производные от входного сигнала. Второе уравнение представляет
формулу перехода от вектора вспомогательных переменных z к вектору
выходных сигналов y.
Следует иметь в виду, что квадратные матрицы
A
(p)
в вариантах
описания (4.2.2) и (4.2.3) имеют различные размеры (в первом случае
s
s×
, во
втором –
r
). Размеры матриц
r×
B
(p)
в этих описаниях также различны.
Пусть через
обозначены порядки столбцов матрицы
1 r
m ,...,m
A
(p)
в
описании (4.2.3), понимая под порядком столбца наибольшую из степеней
входящих в него полиномов. Указанные порядки связаны с общим порядком
системы неравенством
. Путем эквивалентных преобразований
системы (4.2.3) систему можно привести к так называемой правильной
столбцовой форме, у которой общий порядок системы будет равен сумме
порядков столбцов матрицы
1 r
nm ...m≤++
A
(p)
.
Такая форма, как и правильная строчная форма, находит применение
при исследовании и моделировании многомерных систем. Целые числа
, характеризующие правильную столбцовую форму, называются
структурными показателями управляемости системы.
1 r
m ,...,m
4.3. Описание в пространстве состояний
Альтернативой рассмотренным выше вход-выходным видам описания
скалярных и многомерных объектов и их моделей является описание в
пространстве состояний. Кроме входных и выходных переменных в него
входят внутренние переменные объекта
12 n
x
,x ,...,x
, полностью
характеризующие состояние объекта.
Стандартное описание системы S (рис. 4.0.1) в пространстве состояний
имеет вид
x
Ax Bu, y Cx Du=+ =+
, (4.3.1)
где
x
,u,y – векторы состояний, входов (входных воздействий) и выходов
126
