Асанов А.З. Введение в математическое моделирование динамических систем
Подождите немного. Документ загружается.

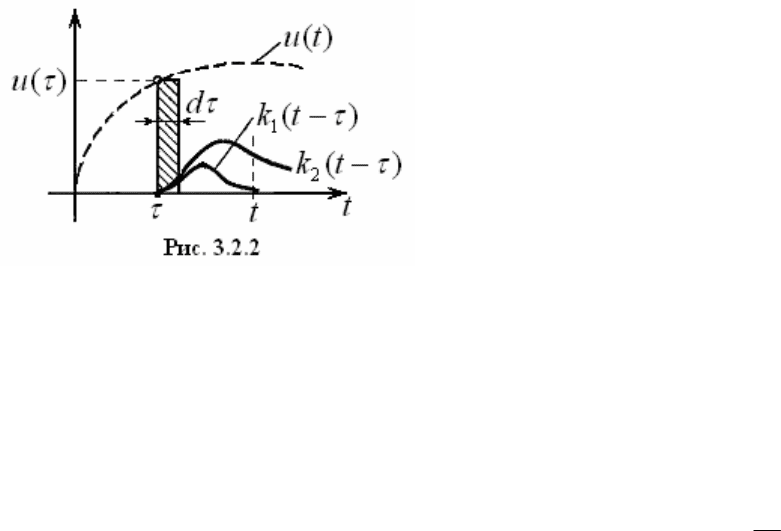
систему сводится к непрерывной совокуп-ности импульсов величиной
()ud
τ
τ
. Но реакция системы на единичный импульс в виде дельта-функции,
приложенной к системе в момент времени
t
τ
=
, известна – эта импульсная
переходная функция
(wt )
τ
−
. Очевидно, что реакция системы на импульс
величиной
()ud
τ
τ
, приложенной к системе в тот же момент времени
t
τ
=
,
будет равна
()()wt u d
τ
ττ
−
. Тогда реакция системы на всю совокупность
импульсов, т.е. на управляющее воздействие
, будет определяться
формулой
()ut
0
() ( ) ( )
t
yt wt u d
τ
ττ
=−
∫
, называемой интегралом Дюамеля, т.е.
будет состоять из суммы реакций на каждый импульс в отдельности.
Пусть
является моментом наблюдения за реакцией системы ,
разность (
t
t ()yt
τ
−
) – интервалом времени между моментом приложения к
системе импульса
()ud
τ
τ
и текущим (рассматриваемым) моментом времени
t
τ
>
. Таким образом, функция
(wt )
τ
−
будет определять степень участия
импульсов, приложенных до текущего момента времени, в образовании
значения
реакции системы в текущий момент времени. Очевидно, что
влияние импульсов, предшествующих моменту времени
, на значение
величины
будет зависеть от характера импульсной переходной
функции
()yt
t
()yt
(wt )
τ
−
. Для примера, из рис.3.2.2 видно, что импульс
()ud
τ
τ
проявляет в момент времени
более
существенно, если импульсная
переходная функция имеет вид
t
2
()wt
τ
−
.
Если же эта функция имеет вид
1
wt()
τ
−
,
то влияние импульса будет проявляться
значительно слабее. Следовательно,
импульсная переходная функция как бы
«взвешивает» роль каждого импульса, приложенного к системе в момент
времени
t
τ
=
, в образовании реакции системы в рассматриваемый момент
времени
t
τ
>
. Поэтому часто импульсную переходную функцию называют
также
весовой функцией.
Учитывая, что взаимосвязь между функциями
()t
δ
и в классе
обобщенных функций представима соотношением
1( )t
() 1()
d
t
dt
δ
= t
, можно
97
записать соотношения, связывающие функции
и
()wt ()ht
() ()
d
wt ht
dt
=
или
0
() ( )
t
ht w d
τ
τ
=
∫
Тогда при известных временных характеристиках (моделях) можно
вычислить реакцию системы на любой произвольный входной сигнал
,
используя интеграл Дюамеля
u( t )
00
tt
y( t ) u( )w( t )d u( t )w( )d
τ
ττ τ τ
=−=−
∫∫
τ
.
Пример вычисления переходной функции динамического звена, описываемого
дифференциальным уравнением
3 () 3 () () ()yt yt yt ut++=
.
Требование найти переходную функцию означает, что
)(1)( ttu
=
и решение
необходимо искать при нулевых начальных условиях.
Известно, что общее решение дифференциального уравнения имеет вид
() () ()
св вын
yt y t y t
=
+
,
где
– свободное движение системы, определяемое при отсутствии внешнего
воздействия, как решение уравнения
)(ty
св
0)()(3)(3 =++ tytyty
, – вынужденное
движение системы, описываемое решением неоднородного дифференциального
уравнения
)(ty
вын
1)()(3)(3 =++ tytyty
при заданных начальных условиях.
При нахождении переходной или весовой функций начальные условия должны быть
положены равными нулю.
Решение однородного уравнения требует нахождения корней характеристического
уравнения 0133
2
=++
λλ
. Корни описываются соотношениями
12
31 31
,
62 62
jj
λλ
=− + =− −
.
Тогда
3
6
12
()
22
t
св
tt
yt e CCos CSin
−
⎛⎞
=+
⎜⎟
⎝⎠
.
Для определения
требуется решение неоднородного дифференциального
уравнения. Поскольку правая часть уравнения представляет собой константу, то решение
будем искать в виде
)(ty
вын
()
вын
ytA
=
.
В результате подстановки в неоднородное уравнение имеем
1(
вын
)
A
yt
=
=
.
Общее решение дифференциального уравнения имеет вид
3
6
12
() () () 1
22
t
св вын
tt
yt y t y t e CCos CSin
−
⎛⎞
=+ =+ +
⎜⎟
⎝⎠
.
Из начальных условий
0
26
3
)0(,01)0(
2
11
=+−==+=
C
CyCy
можно получить
3
3
,1
21
−=−= CC
.
Таким образом, общее решение дифференциального уравнения описывается
98
3
6
3
() 1
23 2
t
tt
y t e Cos Sin
−
⎛⎞
=+ − −
⎜⎟
⎜⎟
⎝⎠
Это означает, что аналитическое выражение для переходной функции
динамического звена имеет вид
)(th
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−+=+=
−
23
3
2
1)()()(
6
3
t
Sin
t
Cosetytyth
t
вынсв
.
Аналитическое выражение для весовой функции
определяется аналогичным
образом, полагая, что
)(tw
)()( ttu
δ
=
.
Графики переходной и весовой функций приведены на рис. 3.2.1.
Рис. 3.2.1. Графики переходной и весовой функций
3.3. Частотные характеристики динамических систем
Исследование динамических систем, как было уже установлено,
сопряжено с рассмотрением сигналов на входе и выходе системы. Одним из
таких методов является рассмотрение спектральных характеристик входного
и выходного сигналов.
Известно, что любой сигнал (сигнал любой формы) может быть
представлен в виде суммы гармонических (синусоидальных) сигналов.
Разложение сигналов на сумму гармонических составляющих может
быть
осуществлено с помощью разложения в ряд Фурье (периодические сигналы)
и преобразования Фурье (сигналы произвольной формы).
Ряды Фурье. В теории доказано, что периодическая функция
()
f
t
,
имеющая период
, может быть разложена на сумму косинусов и синусов
углов, кратных углу
T
2
T
π
ω
∆= . Если период функции 2T
π
=
, то
22
1
2T
π
π
ω
π
∆===
, тогда ряд Фурье имеет вид
(
0
1
() cos sin
2
kk
k
a
)
f
taktb
∞
=
=+ +
∑
kt
, (3.3.1)
99
где
0
1
()aftdt
π
π
π
−
=
∫
,
1
()cos
k
aftkt
π
π
π
−
=
∫
dt
,
1
()sin
k
bftkt
π
π
π
−
=
∫
1, 2, 3, ...k =dt
,
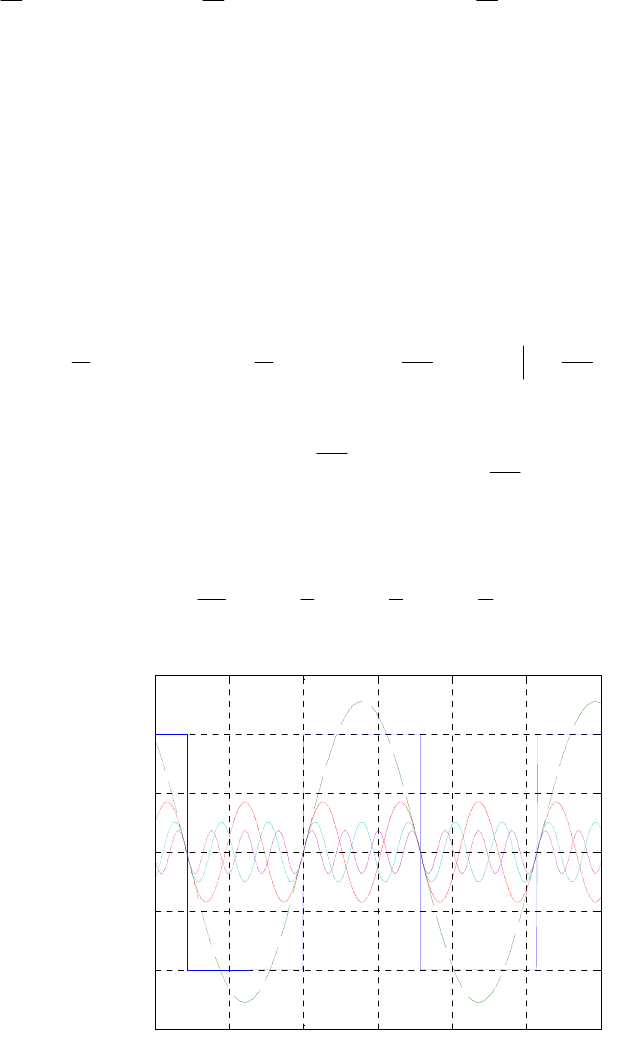
Пример. Разложить на сумму гармонических составляющих совокупность
прямоугольных импульсов, определяемую функциональной зависимостью
при 0,
()
при 2.
at
ft
at
π
π
π
≤≤
⎧
=
⎨
−≤
⎩
≤
Полагая, что ряд (3.1.1) сходится, требуется найти коэффициенты разложения
,
, .
0
a
k
a
k
b
Так как функция
()
f
t
нечетная, то
0
0a
=
,
0
k
a
=
,
1, 2, 3, ...k
=
Коэффициенты
принимают вид
k
b
[][]
()
0
0
1222
()sin sin cos cos 1
0 при четное
2
11
4
при нечетное
k
k
aa
b f t kt dt a kt dt kt kt
kk
k
a
a
k
k
k
ππ
π
π
ππππ
π
π
−
===−=−+
−
⎧
⎪
⎡⎤
=−−=
⎨
⎣⎦
−
⎪
⎩
∫∫
=
Следовательно, ряд Фурье для рассматриваемой функции
()
f
t
имеет вид суммы
бесконечного числа гармоник (рис.3.3.1)
4111
( ) sin sin 3 sin 5 sin 7 ...
357
a
ft t t t t
π
⎡⎤
=++++
⎢⎥
⎣⎦
.
-4 -2 0 2 4 6 8
-1.5
-1
-0.5
0
0.5
1
1.5
Рис. 3.3.1. Гармонические составляющие сигнала
Примечание. Разложение заданной функции
()
f
t
в ряд Фурье означает, что функция
продолжена периодически вне приведенного выше интервала на всю ось
. Функция,
получившаяся в результате продолжения заданной функции
0t
()
f
t
, будет периодической
функцией с периодом
2
π
; на интервале (
0, 2
π
) эта новая функция совпадает с заданной
функцией
()
f
t
. Гармоники полученной периодической функции, суммируясь на
интервале (
0, 2
π
), составляют значения заданной функцией
()
f
t
.
Таким образом, в виде суммы гармонических составляющих может быть
представлена не только периодическая функция, допускающая разложение в
100

ряд Фурье. Ряд Фурье для непериодической функции
()
f
t
, заданной,
например, в интервале
(
,
)
π
π
−
, совпадает с рядом Фурье для функции,
периодически продолженной на всю ось
. 0t
При разложении периодических функций на сумму гармоник,
необходимом при решении целого ряда задач исследования динамических
систем, часто ограничиваются учетом только нескольких первых гармоник, а
остальные отбрасываются, т.е. функция
()
f
t
приближенно представляется в
виде конечного тригонометрического многочлена
(
0
1
() cos sin
2
n
kk
k
a
)
f
taktb
=
=+ +
∑
kt
. (3.3.2)
В этом случае представление функции с помощью гармонических
составляющих производится с точностью, зависящей от числа отброшенных
членов тригонометрического ряда.
Совокупности коэффициентов
, разложения функции
k
a
k
b
()
f
t
в ряд
Фурье называются частотными спектрами этой функции. Очевидно, что
и ; следовательно, спектры являются функциями,
зависящими от номера гармоники
. При этом частотные спектры имеют
дискретный характер. Расстояние между отдельными линиями спектра в
общем случае равно
()
kk
aak= ()
kk
bbk=
k
ω
∆ . Если период функции
()
f
t
равен 2
π
, то
расстояние между линиями равно единице.
Интеграл Фурье. Интеграл Фурье можно ввести как предельный пере-
ход (
T ) при разложении в ряд Фурье непериодической функции →∞
()
f
t
:
[
0
1
() ( )cos ( )sin
]
f
tG tS td
ω
ωωω
π
∞
=+
∫
ω
d
, (3.3.3)
где
() ()cosGf
ω
τωτ
∞
−∞
=
∫
τ
d
,
() ()sinSf
ω
τωτ
∞
−∞
=
∫
τ
,
0
ω
≥
.
Сравнивая разложения (3.3.1) и (3.3.3), нетрудно увидеть определенную
аналогию между рядом и интегралом Фурье. В обоих случаях функция
()
f
t
раскладывается на сумму гармонических составляющих. Однако в ряде
Фурье смежные частоты отличаются друг от друга на величину
ω
∆
. В
интеграле Фурье частоты смежных гармоник непрерывно переходят одна в
другую, т.е. отличаются на величину бесконечно малую.
Интеграл Фурье для функции
()
f
t
может быть представлен в
101

комплексной форме:
1
() ()
2
jt jt
f
tedfte
ωω
ω
π
∞∞
−
−∞ −∞
=
∫∫
dt
dt
.
Обозначим
, тогда
() ()
jt
Ffte
ω
ω
∞
−
−∞
=
∫
1
() ( )
2
jt
f
tFje
ω
d
ω
ω
π
∞
−∞
=
∫
.
Функция
()
F
j
ω
называется преобразованием Фурье функции
()
f
t
. Эта
функция характеризует спектральный состав
()
f
t
и называется также
спектральной плотностью или спектральной характеристикой функции
(сигнала)
()
f
t
.
3.3.1. Преобразование Фурье и его свойства
Прямому преобразованию Фурье могут быть подвергнуты функции
()
f
t
,
удовлетворяющие условиям Дирехле и являющиеся абсолютно
интегрируемыми на всей оси
0t
() ()
jt
Ffte
ω
ω
∞
−
−∞
=
∫
dt
. (3.3.4)
Символически эта формула часто записывается в виде
{
}
() ( )
F
ft Fj
ω
=
.
Суть преобразования (3.3.4) заключается в том, что некоторой функции
()
f
t
действительной переменной ставится в соответствие другая функция
t
()
F
j
ω
комплексного аргумента
j
ω
. Часто функцию
()
F
j
ω
называют
функцией-изображением (или просто изображением) функции-оригинала
(или просто оригинала)
()
f
t
. Еще одно название функции
()
F
j
ω
–
спектральная характеристика функции
()
f
t
.
Обратное преобразование Фурье выражается формулой
1
() ( )
2
jt
f
tFje
ω
d
ω
ω
π
∞
−∞
=
∫
, (3.3.5)
которая позволяет по известной функции
()
F
j
ω
определить ей
соответствующую функцию
()
f
t
. Символически такое преобразование
отображается так:
{
}
1
() (FFj ft
ω
−
= )
.
Часто при исследовании динамических систем функция
()
f
t
характеризует процесс, имеющий место лишь начиная с некоторого момента
времени
, который можно принять за нулевой момент. В этом случае
t
102

() 0
f
t ≡
при и формула (3.3.4) принимает вид 0t <
0
() ()
jt
Ffte
ω
ω
∞
−
=
∫
dt
. (3.3.6)
Преобразование, определяемое формулой (3.3.6), называется
односторонним преобразованием Фурье.
Обратное преобразование Фурье, соответствующее прямому
одностороннему преобразованию (3.3.6), остается двусторонним по
переменной
ω
и дается, как и раньше, формулой (3.3.5).
Пример.
Требуется найти спектральную характеристику функции
при 0
()
0 при 0
t
e
ft
t
α
−
⎧
≥
=
⎨
t
<
⎩
, причем
0
α
>
.
Используя формулу (3.3.6), получим
()
0
0
11
()
tjt jt
Feedt e
jj
αω αω
ω
α
ωα
∞
∞
−− −+
==− =
++
∫
ω
,
т.е.
{}
1
,0
t
Fe t
j
α
αω
−
=≥
+
.
Свойства прямого и обратного преобразований Фурье могут быть
доказаны с помощью непосредственного применения преобразований (3.3.4)-
(3.3.6).
Здесь доказательства не приводятся, при необходимости их можно изучить по
специальной математической литературе.
Приведем лишь краткую сводку свойств
преобразования Фурье, наиболее часто используемых при описании и
анализе динамических систем.
Свойства преобразования Фурье.
Здесь и далее будем полагать, что
{
}
11
Ff(t) F(j)
ω
= ,
{
}
22
Ff(t) F(j)
ω
= и т.д., а также выполнены все другие условия
математического характера.
1. Линейность преобразования
11
() ( )
nn
ii ii
ii
Fcft cFj
ω
==
⎧⎫
=
⎨⎬
⎩⎭
∑∑
, , где = const.
1
11
() ()
nn
ii ii
ii
FcFj cf
ω
−
==
⎧⎫
=
⎨⎬
⎩⎭
∑∑
t
i
c
2.
Дифференцирование и интегрирование оригинала
d
F
f(t) j F( j )
dt
ω
ω
⎧⎫
=
⎨⎬
⎩⎭
,
()
n
n
n
d
Ff(t)jF(j
dt
)
ω
ω
⎧⎫
=
⎨⎬
⎩⎭
.
При одностороннем преобразовании Фурье
0
d
F
f(t) j F( j ) f( )
dt
ωω
⎧⎫
=
−+
⎨⎬
⎩⎭
, где
)(lim)( tf0f
0t +→
=
+
.
103

() ()
1
0
n
n
ni
ni
n
i
d
Ff(t)jF(j) jf(
dt
ωω ω
−
=
⎧⎫
=−
⎨⎬
⎩⎭
∑
)
+
,
где
– некоторая постоянная величина.
)( 0f
-1
+
0
1
() ( )
t
Fft Fj
j
ω
ω
⎧⎫
=
⎨⎬
⎩⎭
∫
и т.д.
3.
Смещение в области оригиналов и в области изображений
{
}
ja
Ff(t a) e F(j)
ω
ω
−
−= , ,
0a >
{
}
at
F
ef(t) F(j a)
ω
=
− .
4.
Изменение масштаба
t
Ff aF(ja)
a
ω
⎧⎫
⎛⎞
=
⎨⎬
⎜⎟
⎝⎠
⎩⎭
, где а – вещественное положительное число.
5.
Умножение в комплексной и действительной областях
{}
12 1 2
1
2
F
f(t) f (t) F(j j )F( j )d
ω
ρρ
π
∞
−∞
⋅= −
∫
ρ
,
12 12
F f(t )f( )d F(j )F(j )
τ
ττ ω ω
∞
−∞
⎧⎫
−=
⎨⎬
⎩⎭
∫
.
6.
Дифференцирование и интегрирование изображения
{}
()
d
Ftf(t) F(j )
dj
ω
ω
=−
,
0
1
Ff(t) F(j)d
t
ω
ω
∞
⎧⎫
=
⎨⎬
⎩⎭
∫
.
7.
Теорема Парсеваля
12 1 2
1
() () ( ) ( )
2
f
tftdt Fj F j d
ω
ωω
π
∞∞
−∞ −∞
=−
∫∫
3.3.2. Частотные характеристики
Рассмотрим линейную динамическую систему. Пусть на вход системы
воздействует некоторый сигнал
. В результате приложения воздействия в
системе возникает переходной процесс, который с течением времени
стремится к нулю, так как система предполагается устойчивой. По истечении
некоторого отрезка времени в системе устанавливается процесс, называемый
установившимся процессом и характеризуемый выходным сигналом
.
Такой подход позволяет использовать спектральные характеристики для
характеризации динамической системы.
()ut
()yt
Частотные характеристики устанавливают связь между спектральными
характеристиками входного сигнала
(Uj)
ω
и выходного сигнала
()Yj
ω
.
Комплексные функции
(Uj)
ω
и
(Yj)
ω
представляют собой преобразование
104

Фурье от входного и выходного сигналов:
() ()
00
jt jt
U j u( t )e dt; Y j y( t )e dt
ωω
ωω
∞∞
−−
==
∫∫
,
где
ω
– частота гармонического сигнала,
2
1j
=
−
.
Комплексной частотной характеристикой (амплитудно-фазовой
частотной характеристикой – АФЧХ) принято называть функцию, представ-
ляющую собой отношение спектральных характеристик выходного сигнала к
спектральной характеристике входного сигнала
()
Y( j )
Wj
U( j )
ω
ω
ω
=
, (3.3.7)
которая учитывает изменение спектральной характеристики сигнала при его
прохождении через линейную динамическую систему.
АФЧХ является комплексной функцией и может быть представлена в
различных формах, например, алгебраической, показательной и т.д.
j
argW ( j )
Y( j )
W( j ) P( ) jQ( ) W( j )e
U( j )
ω
ω
ωωωω
ω
==+=
. (3.3.8)
В инженерной практике наиболее часто используются модуль
()Wj
ω
и
аргумент
arg ( )Wj
ω
комплексной частотной характеристики
()Wj
ω
.
() ( )
A
Wj
ω
ω
=
– называется амплитудно-частотной характеристикой
(АЧХ) и отражает изменение амплитуды гармонических сигналов при
прохождении через систему в зависимости от частоты
ω
.
()arg ( )Wj
ϕ
ω
=
ω
– называется фазо-частотной характеристикой (ФЧХ)
и отражает изменение фаз гармонических сигналов при прохождении через
систему в зависимости от частоты
ω
.
Таким образом, АФЧХ может быть выражена в показательной форме
через АЧХ
()
A
ω
и ФЧХ
()
ϕ
ω
:
(
)
(
)
(
)
j
Wj A e
ϕ
ω
ωω
= . (3.3.9)
В алгебраической форме АФЧХ
(Wj)
ω
может быть представлена
соотношением
(
)
(
)
(
)
Wj P jQ
ω
ωω
=
+
, (3.3.10)
где
() Re ( )PWj
ω
ω
=
– вещественная часть комплексной функции,
называемая вещественной частотной характеристикой (ВЧХ);
105
() Im ( )QWj
ω
ω
=
– мнимая часть функции
(Wj)
ω
, называемая мнимой
частотной характеристикой (МЧХ).
Нетрудно установить, что между различными частотными
характеристиками существуют связи:
() ()
() ()
22
Q( )
A
P( ) Q( ); arctg ;
P( )
P A()cos(); Q A()sin().
ω
ωωωϕω
ω
ω
ωϕω ω ωϕω
=+ =
==
(3.3.11)
Широко в инженерной практике используются логарифмические
частотные характеристики: они, по существу, являются производными от
АЧХ; (например,
() 20lg()
L
A
ω
ω
=
) и ФЧХ, а их графики строятся в другой
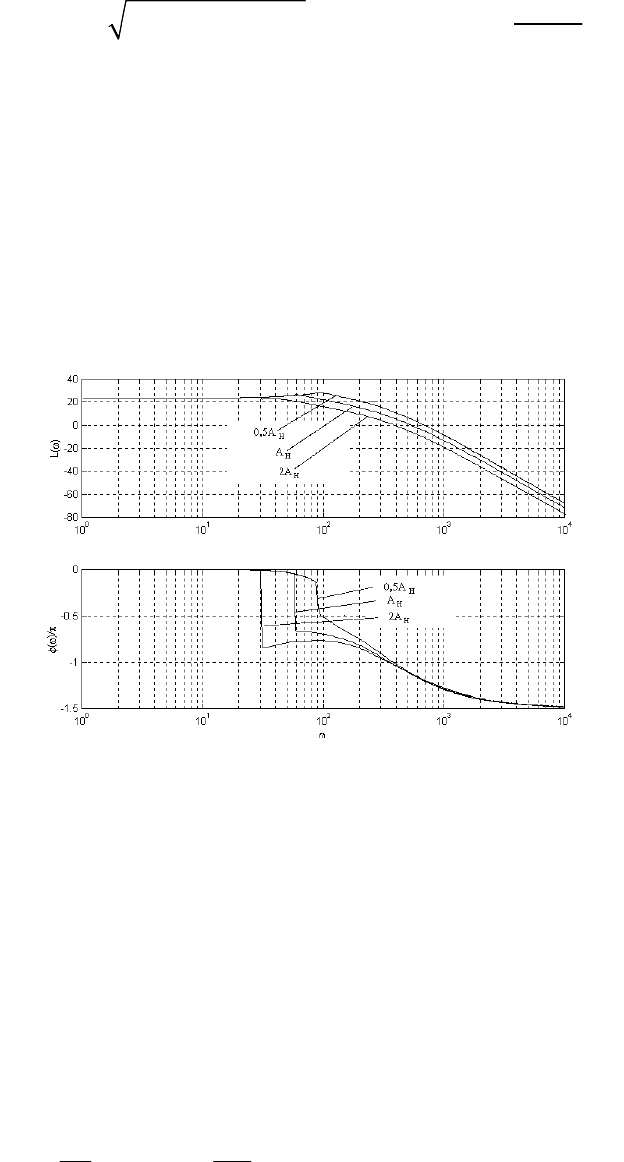
(логарифмической) системе координат. Для иллюстрации на рис.3.3.1
представлено семейство графиков логарифмических АЧХ и ФЧХ для
некоторой нелинейной системы при различных амплитудах сигналов.
Рис.3.3.1 Логарифмические характеристики нелинейной системы
3.3.3. Взаимосвязи частотных и временных характеристик
Рассмотрим линейную динамическую систему, описываемую
дифференциальным уравнением
-го порядка с постоянными
коэффициентами:
n
1
110 1
(n) (n ) (m)
nn m
a y (t) a y (t) ... ay(t) a y(t) b u (t) ... bu(t) bu(t
0
)
−
−
′′
++++=+++
,
где
– выходная (управляемая) величина, – входное (управляющее)
воздействие,
()yt ()ut
(1,)
i
ai n∈ ,
(1,
j
bj m∈ )
– коэффициенты дифференциального
уравнения.
106
