Асанов А.З. Введение в математическое моделирование динамических систем
Подождите немного. Документ загружается.


Для определения характера изменения входного сигнала при
прохождении системы в установившемся режиме подвергнем обе части
уравнения преобразованию Фурье. Используя свойства преобразования
Фурье, получим
() () () () () () ()
1
110 10
nn m
nn m
a j a j ... a j a Y j b j ... b j b U j
ω
ωωωωω
−
−
⎡⎤⎡
++++=+++
⎣⎦⎣
ω
⎤
⎦
,
где
(
)
{
}
()Yj Fyt
ω
=
– изображение по Фурье выходного сигнала ,
()yt
(
)
{
}
()Uj Fut
ω
=
– изображение по Фурье входного сигнала .
()ut
В обеих частях полученного уравнения стоят комплексные функции.
Для их сравнения составим отношение
(
)
()
(
)
(
)
() ()
(
10
10
m
m
n
n
Yj b j ...bj b
Wj
Uj
aj ...aj a
ωω ω
)
ω
ω
ωω
++ +
==
++ +
, (3.3.12)
которое соответствует комплексной частотной характеристике, введенной
ранее.
Рассмотрим качественную сторону рассматриваемых процессов.
Пусть на вход системы воздействует гармонический сигнал
1
() sinut A t
1
ω
=
и требуется определить выходной сигнал в установившемся
режиме.
Можно показать, что спектральная характеристика входного сигнала
имеет вид
() { } ()(
1
11
()
A
Uj Fut
j
)
π
ω
δω ω δω ω
== −−+
⎡
⎤
⎣
⎦
, где
(
)
...
δ
– дельта-
функция (функция Дирака).
Тогда спектральную характеристику выходного сигнала из выражения
(3.3.12) можно выразить следующим образом
() ()() () ()(
1
11
A
Yj Wj Uj Wj
j
)
π
ωωωωδωωδωω
== −−+
⎡
⎤
⎣
⎦
.
Из этого выражения видно, что спектральная характеристика выходного
сигнала в общем случае не совпадает со спектральной характеристикой
входного сигнала. Функциональный множитель
(Wj)
ω
учитывает изменение
спектральной характеристики при прохождении сигнала через линейную
динамическую систему.
Рассмотрим эти выводы подробнее. Пусть, как ранее, на вход воздействует сигнал
1
() sinut A t
1
ω
=
. Представим АФЧХ в показательной форме
arg ( )
() ()
jWj
Wj Wj e
ω
ωω
= (3.3.13)
и найдем выходной сигнал по формуле обратного преобразования Фурье
()yt
107

{} ()()
1
11
11
() () ( )
22
jt jt
A
yt F yt e d W j e d
j
ω ω
π
ω
ωδωωδωω
ππ
∞∞
−∞ −∞
== −−+⎡⎤
⎣⎦
∫∫
ω
.
Используя фильтрующее свойство дельта-функции и учитывая соотношение (3.3.13),
можно получить следующее выражение для установившегося процесса на выходе
системы
11 1 1
arg ( ) arg ( )
1
11
() ( ) ( )
2
jWj jt jWj jt
A
yt W j e e W j e e
j
ωω ω ω
ωω
−−
⎡
⎤
=−−
⎣
⎦
.
Так как
11
()(Wj Wj)
ω
ω
−= ,
1
arg ( ) arg ( )Wj Wj
1
ω
ω
−
=−
, то получим
()()
{
}
()
11 11
arg ( ) arg ( )
1
111
() () ()sin arg()
2
jt Wj jt Wj
A
yt Wj e e AWj t Wj
j
ωω ωω
11
ω
ωω ω
+−+
⎡⎤
=−=+
⎣⎦
. (3.3.14)
Отсюда следует, что в установившемся режиме реакция
линейной
динамической системы на синусоидальное воздействие является также синусоидой.
Угловые частоты входного и выходного сигналов совпадают. Амплитуда синусоиды на
выходе системы отличается от амплитуды входного сигнала в
()yt
1
()Wj
ω
раза, а фазы
отличаются на значение
1
arg ( )Wj
ω
.
Обобщая полученные результаты и используя принцип суперпозиции, справедливый
для линейных систем, можно утверждать, что при воздействии на вход системы
периодического сигнала вида
1
() sin
k
k
ut A t
k
ω
∞
=
=
∑
вынужденное установившееся движение
системы описывается выражением
[]
1
() ()sin arg()
kk k
k
yt A W j t W j
k
ω
ωω
∞
=
=+
∑
.
Таким образом, зная частотные спектры сигнала на входе системы, можно
определить частотные спектры сигнала на выходе системы.
В рассматриваемых соотношениях функция
(Wj)
ω
характеризует
динамические свойства исследуемой системы и не зависит от характера
приложенных к системе воздействий. Эта функция может быть достаточно
легко получена из различных описаний динамической системы –
дифференциальных уравнений, передаточных функций и др.
Пример. Определить частотные характеристики динамической системы,
описываемой дифференциальным уравнением
2
2
2
() 2 () () ()
dd
T yt T yt yt kut
dt dt
ξ
++=
,
где
– постоянная времени системы,
T
ξ
– коэффициент затухания, – коэффициент
усиления системы.
k
По формуле (3.3.12) можно легко получить выражение для амплитудно-фазовой
частотной характеристики рассматриваемой системы
22
()
() 2()1
k
Wj
Tj Tj
ω
ωξω
=
+
+
.
Проведем алгебраические преобразования
()
(
)
()
(
)
()
22 22
2
22
22 22
22 222
1212
()
12
1212
14
TjTkTjkT
kk
Wj
TjT
TjTTjT
TT
ω
ξω ω ξω
ω
ωξω
ωξω ωξω
ω
ξω
−− −−
== =
−+
−+ −−
−+
.
108
Тогда
()
()
22
2
22 222
1
() Re ( )
14
kT
PWj
TT
ω
ωω
ω
ξω
−
==
−+
– вещественная частотная характеристика,
()
2
22 222
2
() Im ( )
14
kT
QWj
TT
ξ
ω
ωω
ω
ξω
−
==
−+
– мнимая частотная характеристика.
Пусть
сек,
0.1T =
0.04
ξ
=
,
1k
=
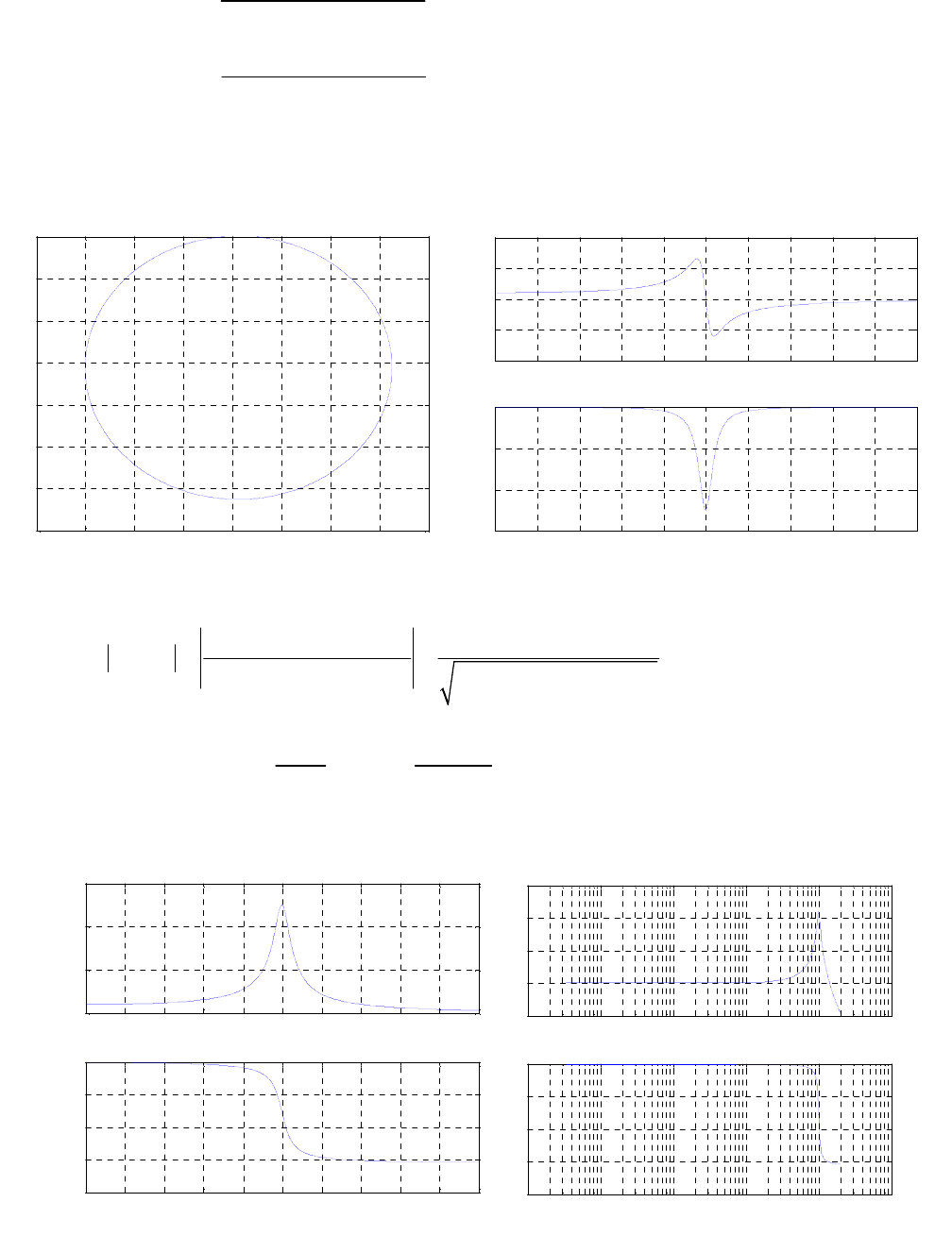
. На рис. 3.3.2 представлены годограф амплитудно-
фазовой частотной характеристики (слева) и графики вещественной частотной
характеристики (ВЧХ) и мнимой частотной характеристики (МЧХ).
-8 -6 -4 -2 0 2 4 6 8
-14
-12
-10
-8
-6
-4
-2
0
P(omega)
Q(omega)
0 2 4 6 8 10 12 14 16 18 20
-10
-5
0
5
10
угловая частота
ВЧХ
0 2 4 6 8 10 12 14 16 18 20
-15
-10
-5
0
угловая частота
МЧХ
Используя соотношения (3.3.11), легко получить выражения для АЧХ и ФЧХ
Рис.3.3.2
. Графики АФЧХ, ВЧХ, МЧХ
()
22
2
22 222
() ( )
()2()1
14
kk
AWj
Tj Tj
TT
ωω
ωξω
ω
ξω
== =
++
−+
– амплитудная частотная
характеристика,
22
() 2
() arg ( )
() 1
Q
Wj arctg arctg
PT
T
ω
ξω
ϕω ω
ω
ω
== =−
−
– фазовая частотная характеристика.
На рис. 3.3.3 представлены амплитудная частотная характеристика (АЧХ) и фазовая
частотная характеристика (ФЧХ) и графики логарифмических АЧХ и ФЧХ
рассматриваемой линейной системы.
Рис.3.3.4
0 2 4 6 8 10 12 14 16 18 20
0
5
10
15
угловая частота
АЧХ
0 2 4 6 8 10 12 14 16 18 20
-4
-3
-2
-1
0
угловая частота
ФЧХ (радиан)
10
-3
10
-2
10
-1
10
0
10
1
10
2
-10
0
10
20
30
угловая частота
ЛАЧХ (дб)
10
-3
10
-2
10
-1
10
0
10
1
10
2
-4
-3
-2
-1
0
ЛФЧХ (радиан)
Рис.3.3.3. Г
р
а
ф
ики АЧХ
,
ФЧХ
,
ЛАЧХ
,
ЛФЧХ
109
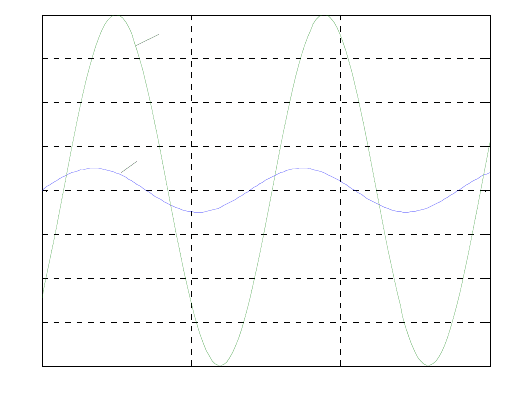
Имея частотные характеристики, можно легко определить параметры выходного
сигнала. Так, при синусоидальном сигнале с амплитудой равной 1 и частотой 9.5 гц на
входе, в установившемся режиме на выходе будет наблюдаться синусоида с той же
частотой, но с амплитудой равной 8 и со сдвигом по фазе на 0.66 радиан (рис.3.3.4) этот
же результат можно получить непосредственно
применяя формулу (3.3.14).
0 0.5 1 1.5
-8
-6
-4
-2
0
2
4
6
8
время (сек)
Амплитуды входного и выходного сигналов
y(t)
u(t)
частота =9.5 гц
Рис. 3.3.4. Графики входного и выходного сигналов
Укажем еще одну связь комплексной частотной характеристики:
0
jt
W( j ) w(t )e dt
ω
ω
∞
−
=
∫
, где – весовая функция системы.
()wt
Частотные характеристики наиболее эффективны при проведении
комплексных исследований систем, сочетающих теоретические и
экспериментальные методы анализа и синтеза динамических систем.
Рассмотрим более подробно связи между частотными и временными
характеристиками линейной динамической системы.
Пусть имеется линейная система с нулевыми начальными условиями и
пусть известна ее АФЧХ. Пусть в момент
времени 0t
=
на вход системы
подается воздействие в виде дельта-функции, т.е.
() ()ut t
δ
=
. Реакция
системы на это воздействие, как уже упоминалось, называется импульсной
переходной функцией
. Импульсная переходная характеристика является
одной из временных характеристик динамической системы.
()yt
()wt
Так как
{
}
() 1Ft
δ
=
, то
{
}
() 1Fut
=
и в соответствии с формулой (3.3.7)
() ()
(
)
Yj Wj Uj
ω
ω
=
ω
или
{
}
(
)
{
}
F
y( t ) W j F u( t )
ω
=
спектральная
характеристика импульсной переходной характеристики есть
{
}
(
)
1Fw(t) W j
ω
=
или, учитывая, что для физически реализуемых (существующих) систем
110
() 0wt ≡
при , можно получить 0t <
{}
0
() () ()
jt
Wj Fwt wte dt
ω
ω
∞
−
==
∫
.
Следовательно, амплитудно-фазовая частотная характеристика системы
является спектральной характеристикой импульсной переходной функции.
Справедлива также формула обратного преобразования Фурье
()
1
() ( ) 0
2
jt
wt W j e d t
ω
ωω
π
∞
−∞
=>
∫
Принимая во внимание последние соотношения и свойство
преобразования Фурье о масштабировании, можно указать еще одно
соответствие между импульсной переходной функцией
и амплитудно-
фазовой частотной характеристикой
()wt
()Wj
ω
:
0
()
jt
t
aW aj w e dt
a
ω
ω
∞
−
⎛⎞
=
⎜⎟
⎝⎠
∫
,
где
– положительная постоянная, не зависящая от
t
и
a
ω
.
Отсюда следует, что если функцию
растягивать (сжимать) вдоль
оси времени
, то соответствующая АФЧХ системы будет сжиматься
(растягиваться) вдоль оси частот
()wt
t
ω
.
Реакцию
системы на воздействие в виде единичной ступенчатой
функции
, как указывалось выше, принято называть переходной
функцией системы
.
()yt
1( )t
()ht
Спектральную характеристику переходной функции можно выразить
следующим образом (учитывая, что
() 0ht
≡
при 0t
<
):
{
}
(
)
{
}
F
y( t ) W j F u( t )
ω
=
,
{
}
(
)
{
}
1
F
h( t ) W j F ( t )
ω
=
,
{} ()
1
Fh(t) W j ( )
j
ω
πδ ω
ω
⎡⎤
=+
⎢⎥
⎣⎦
1
или
()
0
1
jt
Wj ( ) h(t)e dt
j
ω
ωπδω
ω
∞
−
⎡⎤
+=
⎢⎥
⎣⎦
∫
.
Переходная функция является временной характеристикой системы; она
может быть определена с помощью обратного преобразования Фурье:
() () ()
11
0
2
jt
ht W j ( )e d t
j
ω
ωπδωω
πω
∞
−∞
⎡⎤
=+
⎢⎥
⎣⎦
∫
>
.
1
Из-за дельта-функции в правой части равенства, переходная функция (так же как и единичная ступенчатая
функция) преобразуема по Фурье лишь условно.
111

Из свойства преобразования Фурье известно, что умножению
спектральной характеристики на
j
ω
соответствует операция
дифференцирования во временной области, поэтому
[]
1
() ( )1 ( )
2
1
() ()()
22
jt
jt jt
d
ht W j j e d
dt
j
Wj e d Wj e d
ω
ωω
ωπωδω ω
π
.
ω
ωωδωω
π
∞
−∞
∞∞
−∞ −∞
=+ =
=+
∫
∫∫
ω
Используя фильтрующее свойство дельта-функции, получим при
()
Wj
ω
≠∞
, что второе слагаемое равно нулю, следовательно
1
() ( )
2
jt
d
ht W j e d
dt
ω
ω
ω
π
∞
−∞
=
∫
.
Сравнивая полученное соотношение с соотношением для импульсной
переходной функции, получим равенство
() ()
d
wt ht
dt
=
, т.е. импульсная
переходная функция является производной по времени от переходной
функции.
3.4. Передаточные функции динамических систем
Еще одной формой вход-выходного описания динамической системы
(элементов) является передаточная функция.
Этот способ описания динамических систем базируется на методах
операционного исчисления, под которыми понимается совокупность методов
прикладного математического анализа, позволяющих экономными и
непосредственно ведущими к цели средствами получать решения линейных
дифференциальных уравнений, разностных и некоторых интегральных
уравнений.
Сущность операционного
метода заключается в следующем.
Пусть задана некоторая функция
()
f
t
действительной переменной ,
причем такая, что для нее существует преобразование Лапласа (
L -
преобразование)
t
{}
0
() () ( )
st
L
ft fte dt Fs
∞
−
==
∫
.
112
Используя
L
-преобразование, можно каждой преобразуемой по Лапласу
функции поставить в соответствие другую функцию
()
F
s
комплексной
переменной
s
. При этом функцию
()
f
t
принято называть функцией-
оригиналом, или просто оригиналом, а функцию
()
F
s
называется функцией-
изображением, или просто изображением. Преобразование Лапласа
позволяет использовать ряд его весьма удобных для практики свойств.
Например, дифференцированию оригинала
()
f
t
по переменной
соответствует операция умножения изображения
t
()
F
s
на комплексную
переменную
s
, а интегрированию оригинала
()
f
t
по переменной
соответствует операция деления изображения
t
()
F
s
на переменную . Таким
образом, операции дифференцирования и интегрирования оригинала
заменяются в пространстве изображений более простыми алгебраическими
операциями умножения и деления на
p
s
. Это позволяет дифференциальное
уравнение системы заменить в пространстве изображений на алгебраическое
уравнение относительно изображений. Решив это алгебраическое уравнение
относительно изображения
()
F
s
, мы можем получить изображение решения
исходного дифференциального уравнения. Для определения самого решения
можно воспользоваться обратным преобразованием Лапласа
{}
1
1
() () () , 0
2
cj
st
cj
f
tLFs Fseds t
j
π
+∞
−
−∞
==
∫
>
, где .
Recs=
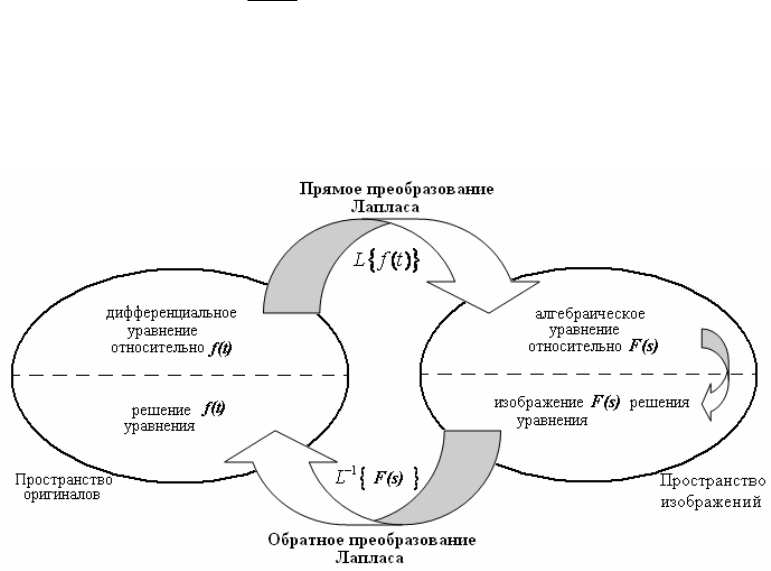
Таким образом, метод решения дифференциального уравнения с
помощью операционного исчисления сводится к схеме, представленной на
рис. 3.4.1
Рис. 3.4.1. Обобщенная схема решения задач с помощью преобразования Лапласа
113

Следует отметить, что во многих случаях при нахождении решения
()
f
t
можно избежать непосредственного вычисления интеграла обратного
преобразования Лапласа, воспользовавшись таблицей соответствий
«оригинал – изображение» и свойствами преобразования Лапласа.
3.4.1. Преобразование Лапласа и его свойства
Как уже отмечалось, сущность преобразования Лапласа заключается в том, что
некоторой функции f(t) действительной переменной t ставится в соответствие другая
функция F(s) комплексной переменной s при условии, что существует (сходится)
интегральное преобразование:
0
(3.4.2)
st
F
(s) L{ f(t)} f(t)e dt
∞
−
==
∫
.
f(t) - называется функцией-оригиналом (или просто оригиналом).
F(s) - называется функцией-изображением (или просто изображением).
Для того, чтобы функция f(t) являлась оригиналом и имела функцию изображения,
необходимо и достаточно выполнение следующих условий:
1.
функция f(t) непрерывна для всех , за исключением, возможно, конечного
числа точек разрыва I рода,
0≥t
2.
функция f(t)=0 для всех значений t<0,
3.
функция f(t) имеет ограниченный порядок роста, т.е. можно указать такие
постоянные числа
и
0>М
0
0
≥С
,
для которых выполняется условие
при t>0.
tC
Metf
0
)( <
Многие функции, встречающиеся при описании процессов в динамических
системах, являются оригиналами. Например, оригиналами являются 1(t),
)(1*sin ttA
ω
,
t
n
1(t), и ряд других. Наличие в этих функциях множителя – единичной
ступенчатой функции – обеспечивает выполнение второго условия. Физическая
интерпретация этого заключается в том, что интересуются некоторым процессом, начиная
с некоторого момента времени t
)0(),(1 >
α
α
te
t
0
. Именно в момент времени t
0
предполагается начало
некоторого воздействия на систему. Часто в линейных системах полагают t
0
=0.
Если хотя бы одно из условий 1-3 не выполняется, то функция f(t) не будет являться
оригиналом. Таким образом, преобразования (3.4.2) являются преобразованиями Лапласа
и условно обозначаются
f(t) F(s)←⎯⎯
i
i
или
f
(t) F(s)
.
Существует и обратное преобразование Лапласа, которое позволяет по известной
функции – изображению определить соответствующую функцию оригинала:
{}
∫
∞+
∞−
−
==
jC
jC
st
dsesF
j
sFLtf )(
2
1
)()(
1
π
114
Свойства преобразования Лапласа.
Приведём без доказательств краткую
сводку свойств преобразования Лапласа. Подробное изложение этих свойств можно
увидеть в специальной литературе [13, 15].
Здесь и далее будем полагать, что , и т.д., а также
выполнены все другие условия математического характера. Все приводимые здесь
свойства можно доказать, используя преобразование (3.4.2) непосредственно.
11
f(t) F(s)←⎯⎯
i
i
2
f(t) F(s)←⎯⎯
i
i
2
1.
Линейность преобразования
)()(
11
sFCtfCL
i
n
i
i
n
i
ii
∑∑
==
=
⎭
⎬
⎫
⎩
⎨
⎧
, , где C
)()(
11
1
tfCsFCL
i
n
i
i
n
i
ii
∑∑
==
−
=
⎭
⎬
⎫
⎩
⎨
⎧
i
= const.
2.
Дифференцирование и интегрирование оригинала
0
d
L
f(t) sF(s) f( )
dt
⎧⎫
=
−+
⎨⎬
⎩⎭
, где
)(lim)( tf0f
0t +→
=
+
,
обобщая –
1
0
n
n
nini
n
i
d
L
f(t) s F(s) s f ( )
dt
−
=
⎧⎫
=
−+
⎨⎬
⎩⎭
∑
,
где
– некоторая постоянная величина.
)( 0f
-1
+
)()()( 0f
s
1
sF
s
1
tfL
1
t
0
++=
⎭
⎬
⎫
⎩
⎨
⎧
−
∫
и т.д.
3.
Смещение в области оригиналов и в области изображений
{
}
as
Lf(t a) e F(s)
−
−= ,
{
}
at
L
ef(t) F(s a)
=
− .
4.
Изменение масштаба
t
Lf aF(as)
a
⎧⎫
⎛⎞
=
⎨⎬
⎜⎟
⎝⎠
⎩⎭
, а – вещественное положительное число.
5.
Умножение в комплексной и действительной областях
12 12
0
t
L f (t )f (t )d F(s) F(s)
τττ
⎧⎫
−−=∗
⎨⎬
⎩⎭
∫
,
{}
12 1 2
1
2
Cj
Cj
L f (t) f (t) F(s )F( )d
j
ω
ωω
π
+∞
−∞
⋅= −
∫
.
6.
Дифференцирование и интегрирование изображения
{}
d
Ltf(t) F(s)
ds
=−
,
0
1
Lf(t) F(s)d
t
∞
⎧⎫
=
⎨⎬
⎩⎭
∫
s
.
7.
Начальное и предельное значения оригинала
0st
lim sF( s ) lim f ( t )
→∞ →+
=
,
0st
lim sF( s ) lim f ( t )
→→∞
=
.
8.
Преобразование периодической функции-оригинала f(t)
{}
1
Ts
F( s )
Lf(t):периодическая
e
−
=−
−
,
где Т – период функции f(t),
– изображение f(t) (в течение одного периода).
F(s)
9.
Производная по параметру
Пусть
– функция-оригинал, преобразуемая по Лапласу относительно
a)f(t,
115
переменной t, – её функция-изображение, a – параметр, не зависящий от t и s.
Справедливы следующие соотношения
a)F(s,
00
t
aa aa
L { lim f ( t,a )} lim F( s,a )
→→
=
,
t
L{ f(t,a)} F(s,a)
aa
∂∂
=
∂∂
, .
00
aa
t
aa
L{ f(t,a)da} F(s,a)da=
∫∫
Из этих формул следует, что соотношение
не нарушится, если в
левой и правой его частях выполнять операции предельного перехода,
дифференцирования и интегрирования относительно параметра а.
f(t,a) F(s,a)←⎯⎯
i
i
В заключение приведем краткую таблицу соответствий «оригинал –
изображение», значительно более подробные таблицы можно найти в
справочниках.
1
1(t)
s
←⎯⎯
i
i
,
1
t
e
s
α
α
−
←⎯⎯
+
i
i
,
1
n
n
n!
t
s
+
←⎯⎯
i
i
,
()
1
nt
n
n!
te
s
α
α
−
+
←⎯⎯
+
i
i
,
2
Sin t
s
2
ω
ω
ω
←⎯⎯
+
i
i
,
2
s
Cos t
s
ω
2
ω
←⎯⎯
+
i
i
,
()
2
2
t
eSint
s
α
ω
ω
α
ω
−
←⎯⎯
++
i
i
,
()
2
2
t
s
eCost
s
α
α
ω
α
ω
−
+
←⎯⎯
++
i
i
,
()
22
2
22
s
tCos t
s
ω
ω
ω
−
←⎯⎯
+
i
i
,
1
1
as
(t a) e
s
−
−←⎯⎯
i
i
,
()()
2
1
1
as
ta ta e
s
−
−−←⎯⎯
i
i
.
Преобразование Лапласа с учетом его свойств и таблица элементарных
операций позволяют свести довольно сложные решения дифференциальных
уравнений к решению алгебраических уравнений в изображениях.
Пример. Требуется решить дифференциальное уравнение
() 5 () 6 () 1yt yt yt
′′ ′
++=
с начальными условиями
,
(0) 3y = (0) 2y
′
=
−
.
Пусть
{
}
() ()Yp Lyt= , тогда с учетом, что
{}
1
1( )
Lt
p
=
и свойств преобразования
Лапласа, получаем уравнение относительно изображения
:
()Yp
()
2
1
() (0) (0) 5 () (0) 6()
pY p py y pY p y Y p
p
′
−−+ −+ =
или
2
1
() 5 () 6() 3 13
pY p pY p Y p p
p
++−−=
или
()
2
1
56()313
ppYpp
p
+
+=++
.
Далее найдем
()
2
2
3131
()
56
pp
Yp
pp p
+
+
=
+
+
Для нахождения оригинала далее можно применить формулу обратного
преобразования Лапласа, которая приведет к вычислению вычетов.
116
