Асанов А.З. Введение в математическое моделирование динамических систем

Подождите немного. Документ загружается.

дифференциального уравнения линейным уравнением с помощью

разложения в окрестности рабочих точек нелинейной аналитической

функции в степенной ряд Тейлора по степеням малых отклонений аргумента

(переменной) и отбрасывания нелинейных членов этого разложения и

составляет первый метод A.M. Ляпунова

Линеаризацию уравнений производят при помощи формулы Тейлора,

которая позволяет разложить нелинейную функцию нескольких переменных

по степеням малых приращений этих переменных, взятых в окрестности их

значений, соответствующих установившемуся режиму. Формула содержит

остаточный член, исследование которого позволяет оценить величину

ошибки, получающейся в том случае, когда ограничиваются первыми

членами разложения. Формула Тейлора, например,

для трех переменных х, у

и z имеет вид

000 000

FFF

F( x,y,z) F(x x,y y,z z) F( x ,y ,z ) x y z

xyz

FFF

yzR

i! x y z

∆∆∆ ∆ ∆ ∆

∆∆∆

∂

∂∂

=+ + += + + +

∂∂∂

⎧⎫

∂∂∂

+++

⎨⎬

∂∂∂

⎩⎭

∑

где

000000

;;;;;

x x y y y z z z x const y const z const=+∆ =+∆ =+∆ = = =

;

–

остаточный член.

Показатели степени, в которую возводятся выражения, стоящие в

скобках, имеют символический смысл. Они указывают на необходимость

выполнения при раскрытии скобок операций, которые можно пояснить на

следующем примере для второй степени:

∆∆

∂∂

∂

+∆∆

∂∂

∂

+∆∆

∂∂

∂

+∆

∂

+∆

∂

+∆

∂

⎟

⎠

⎞

⎜

⎝

⎛

∆

∂

+∆

∂

+∆

∂

222

Частные производные вычисляются в точке с координатами

поэтому являются постоянными.

При линеаризации нелинейных уравнений обычно ограничиваются лишь

членами первого порядка малости, пренебрегая остаточным членом, т. е.

полагают, что

А.М. Ляпунов (1857 – 1918) – великий русский математик, автор теории устойчивости дифференциальных

уравнений и многого другого, самый цитируемый в настоящее время на Западе русский ученый.

000

(, ,) ( , , )

FFF

xyz Fx y z x y z

∂

∂∂

≈+∆+∆+

∂∂∂

∆

Для решения многих задач, например, для исследования устойчивости

системы, такое приближение в большинстве случаев вполне достаточно.

Однако когда линеаризованные уравнения используются для исследования

качества функционирования системы, приращения переменных могут быть

не всегда малыми. Тогда для строгой оценки допускаемой погрешности

проводится анализ остаточного члена, который удобнее всего брать в форме

Лагранжа:

FFF

xyz

ξς

⎡⎤

⎛⎞

∂∂∂

⎛⎞ ⎛⎞

∆+ ∆+ ∆

⎢⎥

⎜⎟ ⎜⎟

⎜⎟

∂∂∂

⎝⎠ ⎝⎠

⎝⎠

⎢⎥

⎣⎦

В последнем выражении

FFF

ης

∂∂∂

⎛⎞⎛⎞⎛⎞

⎜⎟⎜⎟⎜⎟

∂∂∂

⎝⎠⎝⎠⎝⎠

– частные производные,

вычисленные в точке с координатами

ης

<< +∆

00 00

;yyyzzz

<< +∆ << +∆

Найдем выражение приращения

(, ,)

xyz

∆

функции

(, ,)

xyz

, которое

определим как разность между текущим значением этой функции

(, ,)

xyz

ее значением

(, ,)

xyz

в некоторой фиксированной точке, заданной

координатами

000

,,.

Учитывая выражение (2.4.1) с точностью до ,

можно записать

000

(,,) (,,) ( , , )

FFF

xyz Fxyz Fx y z x y z

∂

∂∂

∆≈ − =∆+∆+

∂∂∂

∆

Полученным выражением удобнее всего пользоваться при линеаризации

нелинейных дифференциальных уравнений.

Для того чтобы непосредственно применить найденное из формулы

Тейлора выражение для приращения нелинейной функции к линеаризации

дифференциального уравнения, необходимо несколько преобразовать

последнее.

Составим уравнение установившегося режима для данного элемента

(системы) и вычтем его из уравнения динамики элемента. Тогда в правой

части уравнения будут только приращения нелинейных функций

относительно их значений в установившемся режиме, для определения

которых мы получили выражение из формулы Тейлора.

В качестве установившегося режима может выбираться либо режим,

существовавший до действия возмущения и начала переходного процесса,

либо режим, который установится после затухания переходного процесса.

При установившемся режиме до начала переходного процесса или после его

окончания приращения переменных должны соответственно отсчитываться

от их постоянных значений. Заметим, что если отсчет приращений

переменных (обобщенных координат) производить от их значений при новом

установившемся режиме, наступающем после окончания переходного

процесса, то с течением времени приращения всех переменных стремятся к

нулю (для устойчивых систем).

В качестве примера рассмотрим процедуру формирования

математической модели электромеханической системы (электродвигателя

постоянного тока), где присутствуют все основные положения, изложенные

выше.

Математическая модель электромеханической системы. Действуя согласно

алгоритму формирования модели динамической системы, на первом этапе поставим

задачу составления математической модели электродвигателя постоянного тока с

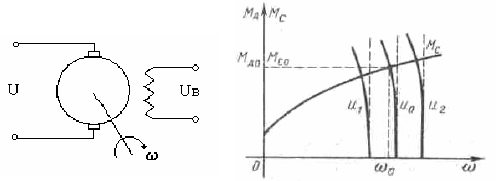
независимым возбуждением (рис.2.4.4)

Требуется найти математические зависимости выходной величины – угловой

скорости вращения вала электродвигателя от управления – входного напряжения U.

Рис.2.4.4 Рис.2.4.

Допущения:

 сопротивление и индуктивность якоря – постоянны;

 реакция якоря скомпенсирована;

 поток рассеяния неизменен;

 момент инерции, приведенный к валу, связанных с валом подвижных частей –

постоянен;

 напряжение источника возбуждения постоянно;

 управление электродвигателем осуществляется с помощью напряжения питания:

Второй этап алгоритма в данном случае не требуется, т.к. нет необходимости

разбивать рассматриваемую систему на простейшие элементы и звенья.

На третьем этапе алгоритма – составлении уравнения динамики выделенного

элемента системы, основным является выявление физического закона, определяющего его

поведение. Обычно таким законом является закон сохранения

вещества, закон сохранения

энергии, второй закон Ньютона или какой-либо из других фундаментальных законов

физики. Математическое выражение соответствующего физического закона, который

определяет процесс, протекающий в данном элементе системы регулирования, и является

исходным дифференциальным уравнением этого элемента.

Для электродвигателя исходным уравнением будет уравнение, выражающее второй

закон Ньютона для вращательного движения

∂

=−

, (2.4.12)

где

– угловая скорость вала двигателя; t – время; J – момент инерции движущихся

частей, приведенный к валу двигателя;

– вращающий момент, приложенный к валу;

– момент сопротивления на валу двигателя.

∂

Следующим шагом должно быть определение факторов, от которых зависят

переменные, входящие в исходное уравнение, и установление выражений,

характеризующих эту зависимость. Зависимости могут быть аналитическими функциями

или заданы графически. В большинстве случаев они являются нелинейными

зависимостями. Подставив найденные выражения в исходное уравнение, получаем

нелинейное уравнение элемента (

системы).

Для нашего примера необходимо установить зависимости переменных

и от

других факторов и переменных. На основании теории электродвигателей можно получить

аналитические выражения функций

∂

),( UMM

∂∂

),( tMM

или представить их

в виде графиков (рис.2.4.5). Вращающий момент

и момент сопротивления

являются нелинейными функциями скорости вращения вала

∂

. Поэтому математическая

модель рассматриваемой системы – уравнение (2.4.12) будет нелинейным дифферен-

циальным уравнением.

Для линеаризации уравнения (2.4.12) перейдем к уравнению в отклонениях от

установившегося режима.

Параметры установившегося состояния находятся из графиков, приведенных на рис.

2.4.5, если положить

oco

∂

Это и есть уравнение установившегося режима. При этом параметры имеют

значения

, . Разложим нелинейные функции

U ),( UMM

∂∂

),( tMM

в ряд

Тейлора в окрестности точки (

, ):

∂∂

⎛⎞ ⎛⎞

=+ ∆+ ∆+

⎜⎟ ⎜⎟

∂∂

⎝⎠ ⎝⎠

()

cco c

∂

⎛⎞

=+ ∆+∆ +

⎜⎟

∂

⎝⎠

tm.

где

),(

000

uMM

∂∂

, – учитывает зависимость момента сопротивления от

времени

; содержат члены порядка малости выше первого относительно

приращений

)(tM

∆

,mm

∆

и .

u∆

Подставим полученные выражения в уравнение (2.4.12) и отбросим члены,

содержащие отклонения в степени выше первой:

000

()

MMM

dt u

ωω

∂∂

∂∂∂

⎛⎞ ⎛⎞ ⎛⎞

=∆+∆−∆−∆

⎜⎟ ⎜⎟ ⎜⎟

∂∂∂

⎝⎠ ⎝⎠ ⎝⎠

После простейших преобразований

00 0

MM M

dt u

∆ω ∆ ∆

ωω

∂∂

⎡⎤

∂∂ ∂

⎛⎞⎛⎞ ⎛⎞

+− = −

⎢⎥

⎜⎟⎜⎟ ⎜⎟

∂∂ ∂

⎝⎠⎝⎠ ⎝⎠

⎣⎦

M(t)

. (2.4.13)

Таким образом, мы получили линеаризованное уравнение в отклонениях (или в

приращениях, в вариациях) от состояния равновесия, выраженное в абсолютных

единицах.

До сих пор при выводе уравнений мы имели дело с абсолютными величинами, с

именованными единицами. Размерность каждого члена уравнения вполне определенная.

В нашем примере каждый член уравнения имеет размерность момента.

Однако при

исследовании динамических систем, особенно при сравнении таких систем и их элементов

между собой, большие удобства представляют уравнения в относительных единицах с

безразмерными коэффициентами или с коэффициентами, имеющими размерность времени

в степени, равной порядку производной, при которой стоит данный коэффициент.

Для приведения дифференциального уравнения в абсолютных приращениях к

уравнению в

относительных единицах с безразмерными коэффициентами произведем

следующие элементарные операции:

1. Разделим все члены уравнения на некоторую постоянную величину, имеющую

размерность членов этого уравнения (в нашем примере – размерность момента). Такой

величиной обычно выбирается номинальное значение, максимальное значение или некото-

рое начальное значение данной переменной.

В рассматриваемом примере возьмем номинальное значение момента

разделим на него почленно уравнение (2.4.13)

00 0

()

HH H H

MM M

Mdt M M u M

ωω

∂∂

⎡⎤

∂∂ ∂

⎛⎞⎛⎞ ⎛⎞

+−∆=∆−∆

⎢⎥

⎜⎟⎜⎟ ⎜⎟

∂∂ ∂

⎝⎠⎝⎠ ⎝⎠

⎣⎦

В результате этого каждый член уравнения стал безразмерным.

2. Перейдем к относительным единицам.

Выберем некоторые постоянные значения для каждой координаты, для всех

переменных, входящих в полученное уравнение. Так, для угловой скорости примем ее

номинальное значение

, для управляющего напряжения – его максимальное значение

. Умножим и разделим каждый член уравнения, в который входит та или иная

переменная, на соответствующую ей выбранную постоянную величину.

max

После этого уравнение в рассматриваемом примере будет иметь следующий вид:

max

00 0

max

()

HH H H H H

MM UM

Jd U

MdtM MuUM

ωωωω

∂∂

⎡⎤

∂∂ ∂

∆∆

⎛⎞⎛⎞ ⎛⎞

+−= −∆

⎢⎥

⎜⎟⎜⎟ ⎜⎟

∂∂ ∂

⎝⎠⎝⎠ ⎝⎠

⎣⎦

3. Введем обозначения относительных единиц и коэффициентов уравнения.

Учитывая, что

∂

∆∂

∂

∆

)(

, можно ввести обозначения

Hmax H H

,g, ,

ωω

∆ω ∆

ωωω

∂

⎛⎞ ⎛⎞

∂∂

== =

⎜⎟ ⎜⎟

∂∂

⎝⎠ ⎝⎠

cmax

HHH

M(t) U M

(t), T, k .

MMMU

∆

∂

⎛⎞

⎜⎟

∂

⎝⎠

Подставляя эти обозначения в полученное уравнение, найдем

( ) () ()

Txkgt

χχ

∂

+− = −

Обозначив

k=−

∂

, окончательно получим

() ()

Tkxkgtf

+= −t

Таким образом, все величины, входящие в уравнение, за исключением времени t и

постоянной Т, приведены к безразмерному виду.

В последнем уравнении

представляет собой выходную координату – отклонение

угловой скорости электродвигателя от номинального значения,

– управляющее

воздействие,

– возмущающее воздействие, приложенное к электродвигателю.

Коэффициент Т имеет размерность времени (сек) и называется постоянной времени

электродвигателя. Отношение

)(tg

)(tf

характеризует зависимость между изменением

выходной координаты х и управляющего воздействия

в установившемся режиме и

называется коэффициентом усиления.

)(tg

На практике пользуются двумя формами уравнений в относительных единицах.

В первой форме, полученной нами выше, время не приводится к безразмерному

виду, и тогда при каждой производной, входящей в дифференциальное уравнение, стоит

коэффициент, имеющий размерность времени в степени, равной порядку производной:

при первой производной

коэффициент имеет размерность сек, при второй производной –

сек

, при третьей – сек

и т. д.

Во второй форме время, как и все другие переменные, приводят к безразмерному

виду. Для этого его относят к некоторой постоянной времени, чаще всего к времени Т, или

так называемой постоянной времени звена.

3. Классические формы математических моделей

скалярных динамических систем

Любая динамическая система является сложной по своему поведению

системой. Как правило, такая система характеризуется целым рядом

различных величин, переменных и т.д. Решая те или иные частные задачи,

нет необходимости учитывать всю совокупность таких характеристик и

переменных – достаточно использовать некоторое подмножество. Поэтому

математические модели системы учитывают и описывают только

определённые стороны

системы. Но и таких математических моделей

множество. Среди математических моделей динамической системы

достаточно часто используют модели, где учитывается одно входное

воздействие и одна выходная (управляемая) переменная (рис. 3.0.1). Такие

системы принято называть скалярными системами (SISO – системами).

Таким образом, для скалярной системы характерно

наличие одного входного (управляющего) и одного

выходного (управляемого) сигнала. При

этом состояние

всей динамической системы может описываться n

переменными состояниями при

. 1n 

Существуют различные способы описания свойств и характеристик

скалярной системы. Наиболее употребительными в практике являются

описанные далее формы моделей, которые могут быть названы

классическими.

3.1. Дифференциальные уравнения n-го порядка

В целом ряде случаев динамическая система может быть описана

неоднородным дифференциальным уравнением вида:

Рис.3.0.1. Скалярная

система

110 1

(n) (n ) (m)

nn m

a y (t) a y (t) ... ay(t) a y(t) b u (t) ... bu(t) bu(t

)

−

′′

++++=+++

, (3.1.1)

где

– выходная (управляемая) величина, – входное (управляющее)

воздействие,

()yt ()ut

(1,)

ai n∈ ,

(1,

bj m∈ )

– коэффициенты дифференциального

уравнения.

В общем случае,

являются функциями времени – это

соответствует нестационарным динамическим системам. Для стационарных

систем характерно то, что и

представляют собой постоянные величины.

Уравнение (3.1.1) устанавливает связь между входным сигналом

и выходной (управляемой) величиной

. Поэтому такое уравнение часто

называют вход-выходным описанием динамической системы. Эта форма

математического описания динамических систем может быть получена из

поэлементного описания (поэлементной (компонентной) модели) системы

путём исключения всех промежуточных переменных.

()ut

()yt

Пример. Пусть поэлементное описание динамической системы представлено

системой уравнений:

dz dy

zyu;

dt dt

dz dy du

zyydt

dt dt dt

+−−=

−−+ ++ =

∫

(3.1.2)

где u(t) – входной сигнал, y(t) – выходной сигнал, z(t) – промежуточная переменная,

осуществляющая связь между элементами системы.

Требуется получить вход-выходное описание вида (3.1.1).

Решение. Продифференцируем второе уравнение (3.1.2), чтобы избавиться от

интеграла. Для упрощения выкладок и для лучшей иллюстрации сути процедуры введём

оператор

. Тогда уравнения (3.1.2) с учётом дифференцирования можно записать:

221

(p )z (p )y u

(p p)z ( p p )y pu

+−+=

−+ + ++=

Далее необходимо осуществить преобразование с тем, чтобы исключить из

уравнений промежуточную переменную z и получить соотношение, связывающее

выходную переменную y(t) с входной переменной u(t).

Умножим каждый из членов первого уравнения на оператор (р

+р), а каждый из

членов второго уравнения на (р+2) и сложим эти уравнения. Тогда

uppuppypppyppp )2()())(1()122)(2(

2222

+++=++−+++

или

или с учётом того, что

upppyppp )3()244(

2323

++=+++

3244

, что является искомым результатом.

Процедура, использованная в данном примере, справедлива для любых

двух дифференциальных уравнений с постоянными коэффициентами. Если L

означает операторную функцию от

, то уравнение можно символически

записать так:

11 12 2 1

21 1 22 2 2

(p)y(t) L (p)y(t) F(t)

Умножим первое уравнение на

, а второе – на

и вычтем одно из

другого. Так как

21 11 1 11 21 1

Ly LLy=

, то получим:

(

)

11 22 21 12 2 21 1 11 2

LL LL y LF LF

−

=− +

аналогично

(

)

11 22 21 12 1 22 1 12 2

LL LL y L F LF−=−+

В общем случае, при наличии системы из

дифференциальных

уравнений процедура получения вход-выходного описания аналогична

приведённой выше.

Пусть

11 1 12 2 1 1

21 1 22 2 2 2

11 2 2

nn nnnn

y L y ... L y F ( t )

yLy...Ly F(t

...................................................

)

yLy...Ly F(t

+++=

+++=)

Так как операторные функции

зависят только от

, то можно

показать, что решение можно получить, используя правило Крамера:

( ) () ( ) ()

iki

yt pFt

∆∆

∑

где

– операторная функция, определяемая определителем:

)( p∆

()

11 12

21 22 2

L L ....

L L .... L

L L ....

∆

– операторная функция, которая является -алгебраическим дополнением

, т.е. является определителем с вычеркнутыми -й строкой и -м

столбцом, умноженным на

)( p∆

ik +

− )1(

Получение вход-выходного описания для систем с переменными

коэффициентами (нестационарные системы) гораздо сложнее.

3.2. Временные характеристики динамических систем

Известно, что решение дифференциальных уравнений вида (3.1.1) при

заданных начальных условиях единственно. Это свойство можно

использовать и описывать динамические системы не дифференциальным

уравнением, а его решением при определенных (заданных, типовых) входных

воздействиях.

При исследовании динамических систем чаще всего в качестве типовых

воздействий используются единичная ступенчатая функция

и дельта

функция

1( )t

(t)

Аналитическое выражение единичной ступенчатой функции

имеет

вид:

1( )

при t

⎧

⎨

≥

⎩

Другим типовым сигналом, часто используемым при исследованиях

динамических систем, является дельта-функция

()t

()

при t

⎧

⎨

∞≠

⎩

() 1tdt

∞

−∞

∫

Переходная характеристика

(переходная функция) системы

определяется как реакция динамической системы на единичное ступенчатое

входное воздействие

при нулевых начальных условиях.

()ht

Аналитически – это есть решение дифференциального уравнения (3.1.1)

при нулевых начальных условиях и при условии

() 1()ut t

Импульсная переходная функция (характеристика) системы – это

есть реакция динамической системы при подаче вход дельта-импульса

()wt

()t

Аналитически – это есть решение дифференциального уравнения (3.1.1)

при нулевых начальных условиях и при условии, что

() ()ut t

Начальный момент воздействия на систему можно принять за начало

отсчета, т.е.

. Тогда, для физически реализуемых систем при

, т.к. выходной сигнал не может появиться раньше входного. Кроме

того, можно доказать, что импульсная переходная функция устойчивых

систем является затухающей функцией.

0t =

() 0wt =

0t <

Переходная и весовая функции динамической системы являются ее

временными характеристиками.

Рассмотрим детальнее роль импульсной переходной функции

()wt

Управляющее воздействие

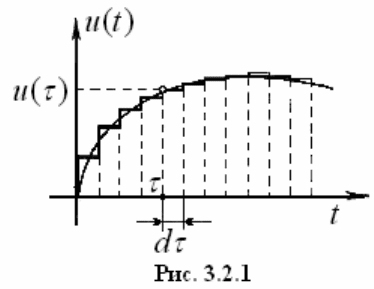
, поступающее на вход динамической

системы, можно аппроксимировать (прибли-

женно представить) ступенчатой ломанной

линией с бесконечно большим числом

ступеней и бесконечно малым шагом каждой

ступени (рис. 3.2.1)

()ut

Таким образом, воздействие

на

(ut)