Асанов А.З. Введение в математическое моделирование динамических систем

Подождите немного. Документ загружается.

где и

представляют собой

изображения по Лапласу для выходного и входного сигналов.

Y( p ) Y( t )exp( pt )dt

∞

=−

∫

p) U(t )exp( pt )dt=−

∫

Пусть известны уравнения состояний динамической системы в

пространстве состояний

X(t) AX(t ) BU(t),

Y(t) CX(t) DU(t).

(5.8.2)

Здесь X(t), U(t), Y(t) – векторные функции времени.

Найдем передаточную функцию передаточной системы, заданной

уравнениями (5.8.2). Применим к этим уравнениям преобразование Лапласа.

С учетом свойств преобразования Лапласа получатся уравнения:

X( p) X( ) AX( p) BX( p),

Y( p) CX( p) DU(p),

−

(5.8.3)

где

– начальные условия.

0X( )

Из первого уравнения выразим вектор

X( p)

(

)

(

)

0X( p) pI A BU( p) pE A X( )

−

=− + −

1−

(5.8.4)

и подставим во второе уравнение

()

(

)

()

0Y( p) C pI A B D U( p ) pI A X( )

−−

=−+ +−

. (5.8.5)

Здесь и далее

– единичная матрица соответствующего размера.

При нулевых (по определению передаточной функции) начальных

условиях, т.е. при

0X( ) 0

, можно найти аналитическое выражение

передаточной функции динамической системы, определяемое через

параметры уравнений состояния:

()

Y( p )

W( p) C pI A B D

U( p)

−

=− +

В общем случае, когда входное воздействие

и выходной сигнал

являются векторами (например, как представлено на рис.5.8.1),

представляет собой матрицу и называется матричной передаточной

функцией (МПФ). Элементами матрицы

являются скалярные

передаточные функции

, характеризующие операторные

коэффициенты передачи от j-го входа системы до ее i-го выхода.

t )

Y(t ) p)

W( p)

W(p)

157

Если система конечномерна и физически реализуема, то скалярные

передаточные функции

являются правильными рациональными

дробями, причем для физически реализуемых систем порядок полинома

числителя меньше порядка полинома знаменателя.

W(p)

Когда система линейна и стационарна, то связь между изображениями

входных и выходных сигналов при нулевых начальных условиях может быть

описана в операторной форме с помощью МПФ следующим образом

Y(p) W( p)U(p)

Описание связей между входными и выходными сигналами во

временной области может быть получено применением обратного

преобразования Лапласа к обеим частям соотношения (5.8.7), и выражаются

эти связи векторным интегралом свертки

Y(t ) w(t )U( )d

ττ

∞

=−

∫

В этой формуле матрица

является оригиналом матрицы и

называет матричной весовой функцией (МВФ). Матричная весовая

функция, также как и МПФ, полностью описывает многомерную

стационарную систему. Элементами этой матрицы являются скалярные

функции

, каждая из которых представляет собой сигнал на i-м

выходе системы при подаче на его

-й вход импульсного воздействия

w( t ) W( p)

w(t)

U(t ) (t )

Если система устойчива и физически реализуема, то с течением времени

все компоненты

экспоненциально стремятся к нулю.

w( t )

Пример.

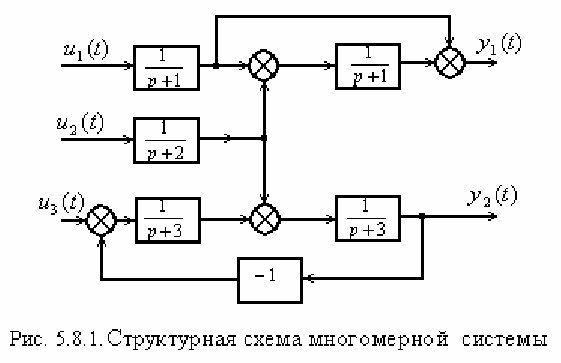
Многомерная динамическая система с тремя входами и двумя выходами

имеет структуру, представленную на рис. 5.8.1.

158

Матричная передаточная функция данной системы имеет вид

11 1 2

2610 61

(p )(p ) (p )(p )

W( p)

(p)(pp)pp

⎡⎤

⎢⎥

++ ++

⎢⎥

+++ ++

⎣⎦

Применяя обратное преобразование Лапласа, можно получить матричную весовую

функцию

()

ttt

(t)e (e e)

w( t )

e(costsint) e e sint

−−−

−−

⎡⎤

+−

⎢⎥

−−

⎢⎥

⎣⎦

3t−

В частном случае, когда система имеет один вход и один выход,

матричная передаточная функция вырождается в обычную скалярную

передаточную функцию. Приведенные выше формулы и соотношения

сохраняют свою корректность и в этом случае.

5.9. Канонические формы уравнений состояний

Из результатов предыдущих разделов можно сделать вывод, что одной

и той же динамической системе с передаточной функцией

bp b p ... bp b

W( p)

ap ...apa

−

++ +

++++

(5.9.1)

может соответствовать множество эквивалентных реализаций в

пространстве состояний и, следовательно, множество схем моделирования.

Что это именно так, можно достаточно легко доказать аналитически. Здесь

мы это посмотрим на примере.

Пусть динамическая система задана уравнениями

[]

26 1

25 1

U, Y

−

⎡

⎤⎡⎤

⎡⎤⎡⎤

=+=

⎡⎤

⎢

⎥⎢⎥

⎢⎥⎢⎥

−−

⎣⎦⎣⎦

⎢⎥

⎣

⎦⎣⎦ ⎣⎦

. (5.9.2)

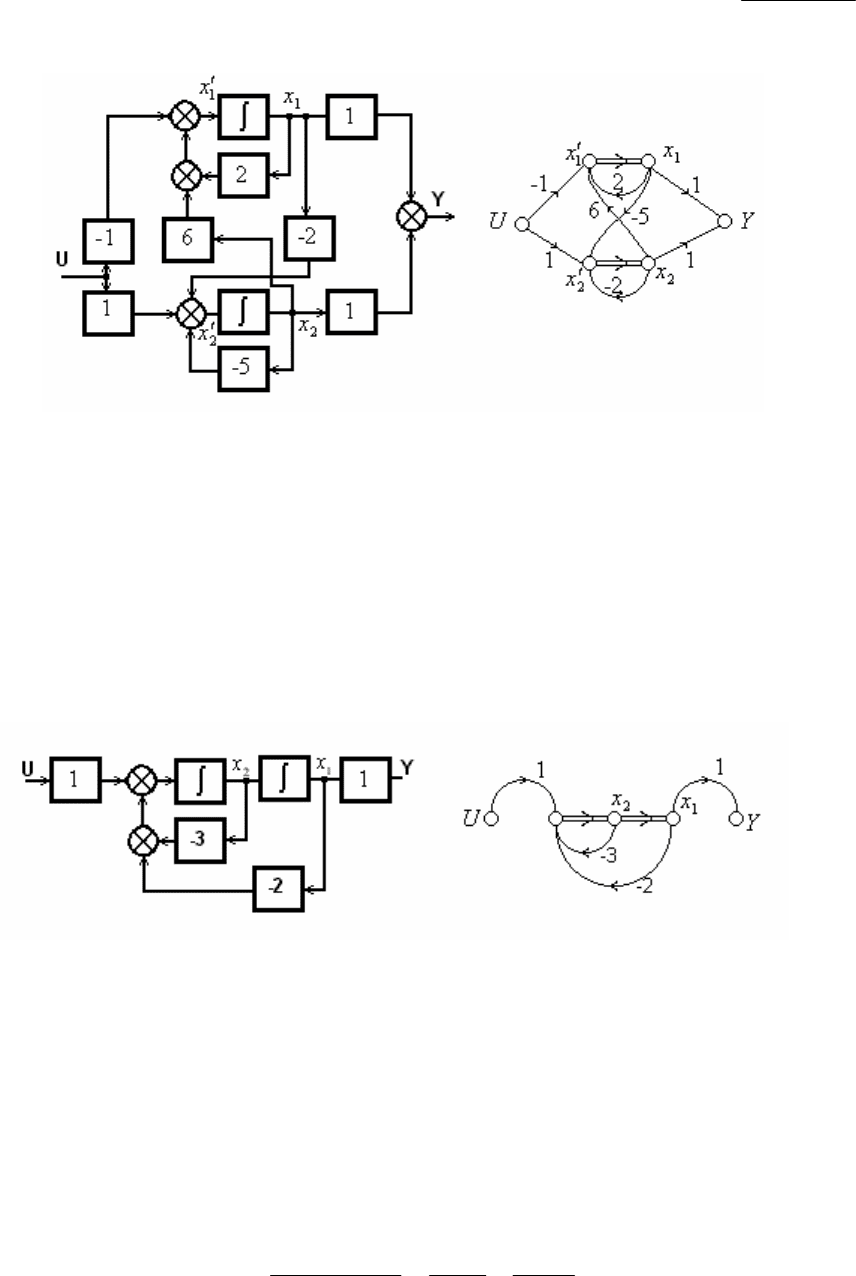
Соответствующие структурная схема и граф системы представлены на

рис 5.9.1.

По структурной схеме и по графу системы нетрудно установить, что

этот вариант реализации динамической системы (5.9.2) отличается большим

количеством связей и сложностью.

159

Передаточная функция, соответствующая системе (5.9.1), при

имеет вид

[]

26 1

25 1

A,B,C

−

⎡⎤ ⎡⎤

⎢⎥ ⎢⎥

−−

⎣⎦ ⎣⎦

p ) C( pE A) B

−

=−=

Рис. 5.9.1. Структурная схема и граф системы

Другая, отличная от структуры на рис. 5.9.1, реализация системы (5.9.1)

по известной передаточной функции может быть получена с помощью

методики, изложенной в разделе 5.5. Так, для рассматриваемой системы

возможно представление

. Структурная

схема и граф этой формы математической модели представлены на рис. 5.9.2.

[]

01 0

23 1

A,B,C

⎡⎤ ⎡⎤

===

⎢⎥ ⎢⎥

−−

⎣⎦ ⎣⎦

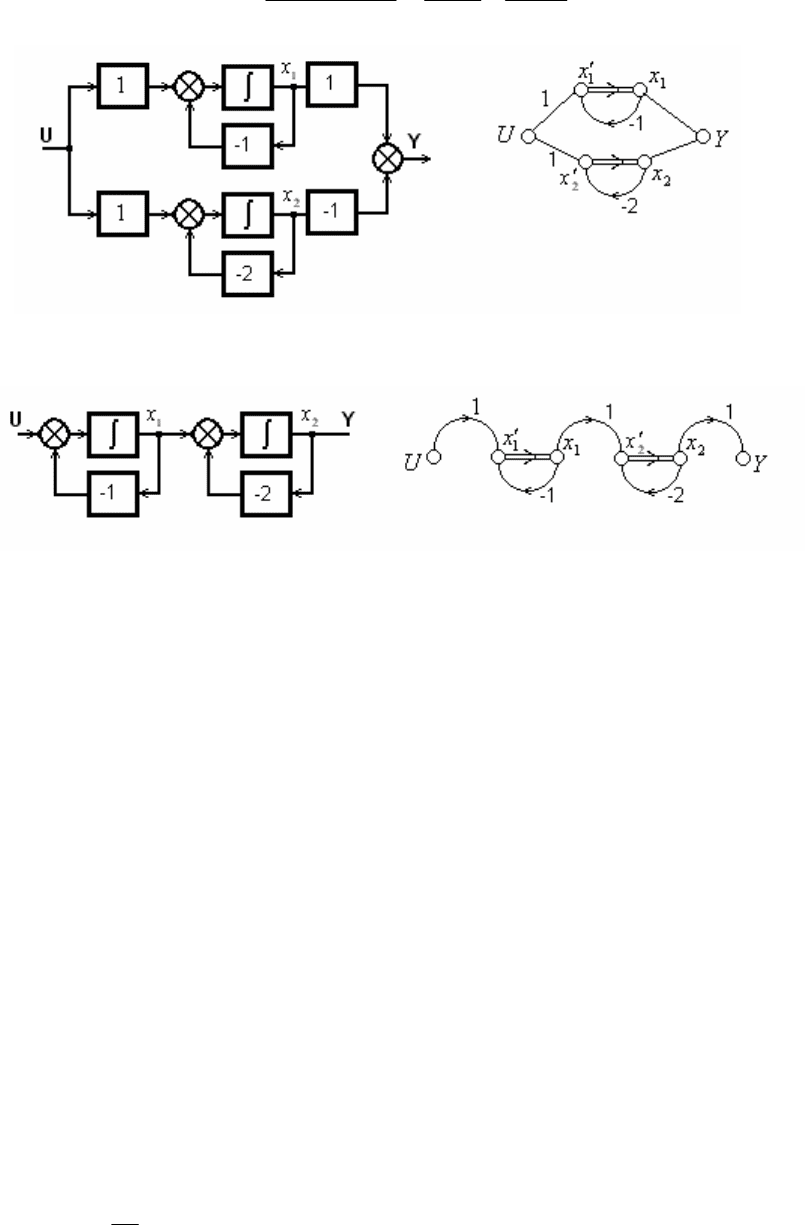
Рис. 5.9.2. Структурная схема и граф системы

Для передаточной функции

могут быть получены и другие

реализации. Так, эти реализации передаточной функции можно представить

как параллельное (рис.5.9.2) и последовательное (рис.5.9.3) соединение двух

апериодических звеньев, что соответствует представлению передаточной

функции динамической системы в виде суммы и произведения простейших

дробей:

32 1

W( p)

pp p p

==−

++ + +

, (5.9.3)

160

32 1

W( p)

pp p p

==×

+++

. (5.9.4)

Рис. 5.9.3. Структурная схема и граф системы (5.9.3)

Рис. 5.9.4. Структурная схема и граф системы (5.9.4)

Рассмотренный пример отчетливо демонстрирует наличие множества

структур моделей, соответствующих одной и той же динамической системе,

одной и той же передаточной функции. Отсюда вытекает необходимость

выбора наиболее рациональной модели (структуры) при математическом

описании динамических систем.

На практике обычно отдают предпочтение так называемым

каноническим реализациям (каноническим формам), отличающимся

простотой математического описания и регулярной

структурой. Это

обеспечивается переходом от исходного описания с помощью замены

переменных X=TZ к такой системе координат, что большинство элементов

матриц A,B,C,D в новой системе координат становятся равными нулю или

единице.

Пусть известно некоторое исходное (условно – "старое") описание

динамической системы:

ст ст ст

X(t) A X(t) B U(t); Y(t) C X(t)

=+ =

. (5.9.5)

Положим, что старые координаты X(t) и координаты в новой системе

описания задаются соотношением X=TZ , где Т – некоторая матрица, а Z(t)

– координаты в новой системе.

161

ст ст ст

нн н

(TZ( t )) A TZ( t ) B U( t ); Y( t ) C TZ( t );

T Z(t) A TZ(t) B U(t); Y(t) C TZ(t);

(t) T A TZ(t) T B U(t); Y(t) C TZ(t);

Z(t ) A Z(t ) B U(t ); Y(t ) С Z(t ),

−−

=+ =

(5.9.6)

где

Z – вектор переменных в новой системе координат.

Таким образом, между матрицами системы в старой и новой системах

координат существуют связи

нст нст нст

нст нст

T A T; B T B ; C C T;

RTR; QTQ,

−−

−

(5.9.7)

где

и , и – матрицы управляемости и наблюдаемости в старой

и новой системах координат, соответственно.

ст

При этом отметим, что

ст ст ст н н н

C(pE A )B C(pE A)B W(p)

−−

−=−=

В общем случае выбор преобразующей матрицы

Т произволен. Но,

конечно, для перехода к определенным формам описания требуется и

определенная матрица

Т. Так, матрица Т может быть составлена из

собственных векторов

матрицы A, т.е. векторов, которые удовлетворяют

уравнению

(A E)t

−=

, где

– собственные числа матрицы

Если

[]

121 2

26 1

25 1

;B;C

;;t;t

λλ

−

⎡⎤ ⎡⎤

⎢⎥ ⎢⎥

−−

⎣⎦ ⎣⎦

−

;

⎡

⎤⎡

=− =− = =

⎤

⎢

⎥⎢

−

⎥

⎣

⎦⎣⎦

121 2

,,t,t

λλ

−

⎡

⎤⎡

=− =− = =

⎤

⎢

⎥⎢

−

⎥

⎣

⎦⎣⎦

, то

[]

23 23

12 12

10 1

02 1

T,T,

TAT , B TB , C CT

−

−−

−

⎡⎤ ⎡⎤

⎢⎥ ⎢⎥

−

⎣⎦ ⎣⎦

−

⎡⎤ ⎡⎤

== == ==−

⎢⎥ ⎢⎥

−

⎣⎦ ⎣⎦

Система с матрицей

примечательна тем, что по диагонали матрицы

стоят собственные числа

, а структура, реализующая такую систему,

имеет простейший вид (рис.5.9.3).

162

Такая система, так же, как и уравнение (5.9.3) с матрицами

, , ,

носит название канонической формы Жордана.

B C

В общем случае, матрица преобразования Т может быть сформирована,

исходя из последних соотношений (5.9.7):

1 T

ст н н ст

TRR, T(QQ)

−

. (5.9.8)

Таким образом, если рассматривать проблему в качественном плане, в

пространстве состояний существуют системы координат, в которых

матрицы

, , имеют простой вид и содержат небольшое число

коэффициентов. Такие математические описания и соответствующие им

схемы моделирования называются каноническими формами.

B C

С инженерной точки зрения канонические формы – это модели

исходной системы, отличающиеся простой структурой и минимальным

числом варьируемых параметров. Совокупность канонических форм

можно рассматривать, как набор типовых моделей динамических систем.

Знание свойств

этих моделей и их характеристик позволяет выбирать

модели, удобные для решения конкретных задач моделирования, анализа и

синтеза систем.

Существуют и строгие математические определения и формулировки

канонических форм, но здесь они не рассматриваются; при необходимости

их можно найти в соответствующей учебно-научной литературе.

Каждую каноническую форму (КФ) можно охарактеризовать

различными способами. Но

наиболее употребительными в практике

являются следующие:

• специальные способы записи передаточной функции динамической

системы (в виде произведения простых дробей, в виде цепной дроби и

т.п.) с указанием правила перехода к структурной схеме;

• указание матрицы преобразования Т исходной системы к канонической

форме.

Например, чтобы охарактеризовать каноническую форму Жордана для

системы с различными вещественными собственными числами, достаточно

указать одно из положений, что

• матрица A системы в этой КФ имеет вид

[, ,..., ]

Adiag

λλ

, а матрица

;

[1,1,...,1]

B =

• схема моделирования представляет собой параллельное соединение

163

апериодических звеньев

()

−

;

• структурная схема (граф) системы строится по передаточной функции

системы, представленной в виде суммы простейших дробей

( ) ...

CC C

pp p

λλ

=+++

−− −

;

• переход к КФ осуществляется с помощью матрицы Т, составленной из

собственных векторов матрицы

исходной динамической системы.

В некоторых случаях возможны и другие способы описания КФ,

например, в терминах весовой или переходной функции динамической

системы. В частности, для КФ Жордана характерно раздельное

моделирование элементарных собственных движений системы, т.е.

представление весовой функции в виде суммы

w( t ) C e C e ... C e

λλ

=+ ++

Теоретически различные способы задания КФ эквивалентны, хотя и

опираются на разный математический аппарат – технику преобразования

рациональных дробей (передаточные функции) в одном случае и методы

линейной алгебры и технику матричных преобразований (описание в

пространстве состояний) в другом. Они позволяют решать одну и ту же

задачу построения КФ различными путями, приходя к

одному и тому же

результату. Но еще более эффективным является объединение указанных

видов описания, когда они дополняют друг друга и позволяют осветить одни

и те же вопросы с разных сторон. Во многих случаях совместное применение

различных способов описания динамических систем позволяет найти

наиболее эффективные и рациональные пути решения поставленных задач

анализа

и синтеза систем, в связи с чем представляется, что специалист в

области систем управления динамическими объектами должен свободно

владеть каждым из них.

Число всевозможных канонических форм достигает нескольких

десятков. Не все они имеют практическое применение. Далее рассмотрим

наиболее распространенные в практике канонически формы Фробениуса и

Жордана, а также каскадных соединений.

164

5.9.1. Фробениусовы канонические формы

Наибольший интерес представляют канонические формы, в которых

структура матриц

А, В, С имеет наиболее простой вид. Причем при

приведении уравнений к канонической форме простую структуру принимают

две матрицы из трех:

и (управляемые КФ) или B

и (наблюдаемые

КФ). Управляемые канонические формы чаще всего используются при

синтезе регулятора, а наблюдаемые – при синтезе наблюдателей.

Основу структурной реализации этих форм составляет цепочка

последовательно включенных интеграторов, охваченных обратными

связями, причем коэффициенты обратных связей совпадают с

коэффициентами характеристического полинома (знаменателя

передаточной функции) динамической системы.

Пусть известна произвольная передаточная функция

p...p

W( p)

pp...p

ββ

αα

−

++ +

, (5.9.9)

т.е. описана динамическая система с одним входом и одним выходом.

Строчная управляемая КФ

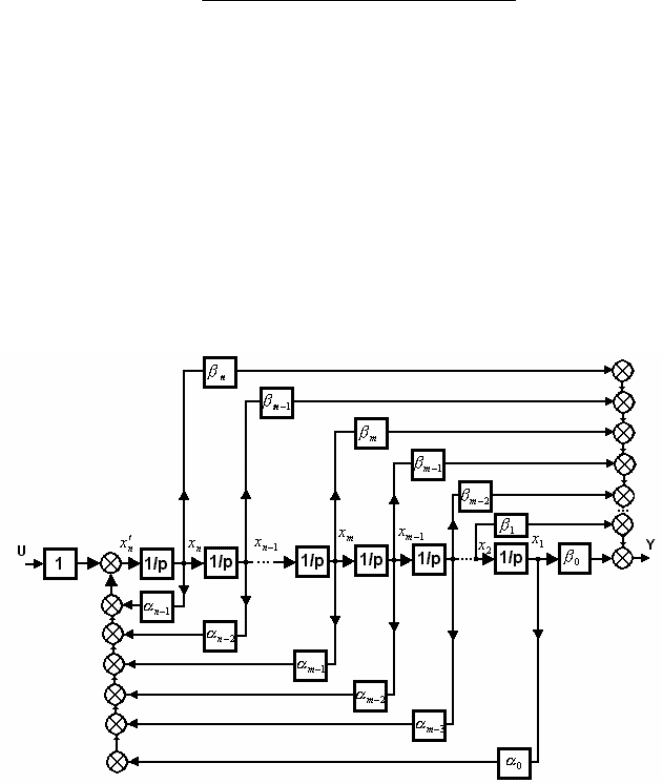
Структурная реализация такой КФ была достаточно подробно

рассмотрена в разделе 2.3. Здесь напомним, что она получена по методу

понижения производной (рис. 5.9.5), а все коэффициенты реализации

совпадают с коэффициентами передаточной функции (5.9.9) и не требуют

дополнительных расчетов.

Рис.5.9.5. Структурная схема строчно-управляемой КФ

165

Система дифференциальных уравнений, соответствующая строчно-

управляемой КФ, получается, если в качестве переменных состояния

1 n

,...,x

принять выходные сигналы интеграторов.

01 12 1

..........

xx... x

Yxx... x

αα α

ββ β

−

⎧

⎪

⎨

⎪

=− − − − +

⎪

=+++

⎩



(5.9.10)

Матричная запись этих уравнений имеет вид

X(t) AX(t) BX(t), Y CX(t)

=+ =

, (5.9.11)

где

012 1

010...0

001...0

... ... ... ... ... , , ...

...

000...1

...

ααα α β

−

−−

⎡⎤

⎢⎥

−−− −

⎣⎦

⎡⎤

⎢⎥

⎣⎦

Матрица

КФ (5.9.11) имеет характерную структуру. Ее правый

верхний блок равен единичной матрице, а последняя строка образована

коэффициентами характеристического полинома системы. В линейной

алгебре матрицы типа A, а также матрицы, получаемые их транспони-

рованием, называются фробениусовыми (в честь немецкого математика

Г.Фробениуса). Такие матрицы обладают рядом интересных свойств; здесь

мы упоминаем лишь одно

свойство, которое нам понадо-

бится в дальнейшем – каждая

строка матричной экспоненты

, где

– матрица Фробе-

ниуса вида (5.9.11), является

производной от предыдущей

строки.

Учитывая специальный вид

матриц

и , фробениусову

КФ (5.9.11) называют строчной

Рис.5.9.6. Граф строчно-управляемой КФ

166