Артюхов В.Г., Ковалева Т.А., Шмелев В.П. Биофизика

Подождите немного. Документ загружается.

логический эффект, предлагается именовать не ОБЭ, а отношением

равных эффектов (независимо от механизма их возникновения).

4. Лучевая болезнь

результате

действия ионизирующих излучений на живые клет-

ки

(биологические объекты) возникают повреждения важных био-

логических молекул и разнообразных

структур

клеток, что влечет

за собой развитие лучевой болезни (лучевого поражения).

Лучевая болезнь - заболевание, возникающее при воздействии

различных видов ионизирующих излучений на организм (человек,

животные, растения). Многообразие проявлений поражающего дей-

ствия радиации на живой организм зависит прежде всего от следую-

щих факторов: вид облучения - общее или местное, внешнее или от

инкорпорированных

радиоактивных веществ; временной фактор -

однократное,

повторное, пролонгированное, хроническое облуче-

ние;

пространственный фактор - равномерное или неравномерное

облучение, облучаемый объем и локализация облученного участка.

Человек, животные, микроорганизмы и растения постоянно под-

вергаются извне действию гамма-излучений земной коры, космиче-

ских лучей и изнутри облучаются находящимися в организме чело-

века в ничтожных количествах радиоактивными веществами (К,

жа,

222

Rn,

C и др.). Лучевая болезнь развивается лишь

тогда,

когда суммарная доза облучения превышает естественный радиоак-

тивный

фон. Чем больше поглощенная доза излучения, тем сильнее

проявляется поражающее действие радиации.

Различают острую

лучевую

болезнь, возникающую от однократ-

ного общего облучения в сравнительно больших

дозах,

и хрониче-

скую

лучевую

болезнь, которая может быть результатом перене-

сенной

острой лучевой болезни или хронического воздействия ма-

лыми дозами.

Характерной чертой

острой

лучевой

болезни

человека является

волнообразность ее клинического течения. А.К.Гуськова и Г.Д.Бай-

соголов

(1970)

предложили выделять три периода в течении острой

лучевой болезни: период формирования, период восстановления и

период исходов и последствий.

Рассмотрим более подробно первый период острой лучевой болез-

ни

- период формирования. Этот период течения острой лучевой бо-

лезни

в свою очередь можно разделить на четыре фазы: 1) фаза

первичной

острой реакции; 2) фаза кажущегося клинического бла-

гополучия (скрытая или латентная фаза); 3) фаза выраженных

311

клинических

проявлений (фаза разгара болезни); 4) фаза раннего

восстановления.

Острую

лучевую

болезнь различают и по степени тяжести радиа-

ционного

поражения, определяемой величиной поглощенной дозы

излучения. Лучевая болезнь человека возникает при облучении в

дозах 1-10 Гр и более (имеется в виду воздействие у-излучения).

После

облучения человека в меньших дозах наблюдают реакции

различной

степени выраженности со стороны отдельных его систем.

В интервале доз 1-10 Гр выделяют три степени тяжести острой

лучевой болезни: острая лучевая болезнь I (легкой) степени (1-2

Гр);

острая лучевая болезнь II (средней) степени (2-4 Гр); острая

лучевая болезнь III (тяжелой) степени (4-6 Гр); острая лучевая бо-

лезнь IV (крайне тяжелой) степени (выше 6 Гр).

Вероятность развития острой лучевой болезни той или иной сте-

пени

тяжести при данной поглощенной дозе излучения определяет-

ся

индивидуальной радиочувствительностью организма. Так, на-

пример,

при дозах 6-10 Гр выявляется переходная форма лучевой

болезни,

которая протекает как III степень, но с поражением ки-

шечника.

Специальное лечение человека может обеспечить его вы-

живание.

При дозах 10-20 Гр развивается типичная форма кишеч-

ного поражения, заканчивающаяся смертельным исходом через 8-

16 суток. При дозах

20-80

Гр отмечается токсемическое поражение

(сосудистая форма поражения). Смерть наступает на 4-7-е сутки

при

мозговой и менингиальной симптоматике. При дозах облучения

выше 80 Гр развивается церебральная форма поражения с колапсом

судорогами, завершающаяся смертью на 1-3-и сутки после воз-

действия радиации.

Критической

системой, степень поражения которой определяет

тяжесть и исход острой лучевой болезни при дозах 1-10 Гр, являет-

ся

система кроветворения и в первую очередь костный мозг.

Хроническая

лучевая

болезнь

- нозологическая форма

лучевого

поражения,

развивающаяся при продолжительном облучении орга-

низма

в малых

дозах.

Эта форма, как и острая лучевая болезнь, ха-

рактеризуется фазностью течения, особенностями проявления, свя-

занными

с неравномерностью облучения, и также имеет отдален-

ные

последствия. Большая

заслуга

в выделении, классификации и

принципах

диагностики хронической лучевой болезни принадле-

жит А.К.Гуськовой. Хроническая лучевая болезнь развивается по

достижении некоторой критической дозы облучения. Она представ-

ляет собой сложный четко очерченный клинический синдром с вов-

лечением большинства органов и систем организма. Хроническая

312

лучевая болезнь у животных сопровождается постепенным ослабле-

нием

сердечной деятельности, нарушением функций желез внут-

ренней

секреции, истощением, ослаблением сопротивляемости ин-

фекционным

болезням. Выраженный синдром хронической лучевой

болезни развивается при суммарных дозах 0,7-1 Гр

(70-100

рад) и

интенсивности

излучения

0,001-0,005

Гр/сут.

После прекращения

облучения человека и животных наступает период восстановления,

который

характеризуется преобладанием репаративных процессов

наиболее радиопоражаемых тканях (кроветворная система, эпи-

телий слизистой тонкого кишечника), а также нормализацией фун-

кциональных

нарушений в

других

системах.

У растений лучевая болезнь возникает под влиянием различных

видов ионизирующих излучений. Наибольшую опасность представ-

ляют а-частицы и нейтроны, нарушающие нуклеиновый,

углевод-

ный

и жировой обмен в растениях. Очень чувствительны к дейст-

вию радиации корни и молодые ткани. Общий симптом лучевой бо-

лезни

растений - задержка их роста. Выявлены видовые, сортовые и

индивидуальные внутрисортовые различия в радиочувствительно-

сти растений. При лучевой болезни повышается восприимчивость

растений к инфекционным болезням.

& 5. Модификация радиочувствительности

Проявление

радиобиологического эффекта может изменяться

под влиянием факторов физической и химической природы, назы-

ваемых

модификаторами

лучевого

поражения. Конечная цель исс-

ледований по вопросам модификации радиочувствительности - это

нахождение путей активного и избирательного воздействия на ра-

диочувствительность, т.е. ослабления ее или усиления в зависимо-

сти от необходимости. Наиболее активно проблема модификаци ра-

диочувствительности, точнее - овладения способами управления

радиочувствительностью, начала развиваться после

1945г.

и в по-

следующий период интенсивного испытания атомного оружия, ког-

да возникла реальная угроза возникновения массовых

лучевых

по-

ражений человека. Во

всех

развитых странах мира внимание уче-

ных в данный период было привлечено к поиску средств противолу-

чевой защиты.

Радиочувствительность биообъектов (биосистем) можно модифи-

цировать разными путями: изменением выходов первичных радиа-

ционно-химических реакций, дезактивацией свободных радикалов

других

активных продуктов радиолиза, активацией или ингиби-

рованием рапарационных, восстановительных процессов и т.п.

313

Процесс

модификации радиобиологичсскх эффектов осуществляет-

ся

на разных уровнях организации клетки, охватывая разные этапы

формирования

лучевого

поражения.

Кислородный

эффект в радиобиологических явлениях

Сильное

влияние на исход

лучевого

поражения организмов и ве-

личины

радиационно-химического выхода превращений многих ти-

пов

биосоединений оказывает свободный кислород в биосистеме.

Речь идет о так называемом кислородном эффекте - универсальном

явлении

радиобиологии.

Кислородный

эффект

- это явление усиления

лучевого

пораже-

ния

организмов в присутствии кислорода (при повышении его кон-

центрации)

по сравнению с поражением при облучении в условиях

гипоксии

или аноксии. Под кислородным эффектом в радиобиоло-

гии

понимают также защитное действие пониженного содержания

кислорода (гипоксии) при облучении живых организмов ионизиру-

ющей радиацией. Кислородный эффект впервые был описан еще в

1909 г. Г.Шварцем. Используя предельно переносимое снижение

концентрации

кислорода во вдыхаемом

воздухе

(для мышей - 7%,

для крыс - 5%),

А.Дауди

и сотр.

(1950)

отметили высокий процент

защиты этих животных, облученных рентгеновскими лучами в аб-

солютно смертельной дозе. Кислородный эффект обнаружен по раз-

личным

показателям

лучевого

поражения как в модельных систе-

мах, так и в экспериментах на

всех

уровнях биологической органи-

зации

(субклеточном, клеточном, тканевом, органном и организ-

менном).

При снижении содержания кислорода в биообъекте значи-

тельно ослабляются все радиобиологические реакции (биохимиче-

ские

нарушения, мутации, угнетение роста и развития) и повыша-

ется выживаемость облученных организмов. В настоящее время

еще полностью не

ясно,

какие свойства кислорода ответственны за

его радиомодифицирующес действие. Механизм защитного дейст-

вия

гипоксии объясняется тем, что при облучении в присутствии

молекулы кислорода, являющейся бирадикалом, образуются перок-

сидные радикалы, которые усиливают действие ионизирующих из-

лучений на жизненно важные макромолекулы и структуры клеток

(или) ослабляют эффективность внутриклеточных защитных ве-

ществ.

Количественным выражением изменения эффекта облучения

под влиянием кислорода служит ФИД (фактор изменения дозы),

который

в данном

случае

называют коэффициентом кислородного

усиления

(ККУ).

Величина кислородного эффекта зависит главным

314

образом

от

вида ионизирующего излучения

условий облучения.

Наибольший

кислородный эффект наблюдается при действии рент-

геновских

у-лучей.

ростом плотности ионизации кислородный

эффект

уменьшается,

при действии наиболее плотно ионизирую-

щих излучений, например а-частиц, исчезает.

Практически

сенсибилизирующее действие кислорода

при

облу-

чении

животных клеток может проявиться только

в том

случае,

когда

он

присутствует непосредственно

момент облучения.

Так,

при

подведении кислорода

клеткам китайского хомячка всего

че-

рез

0,3 мс

после облучения значение

ККУ

падало

с 2,6 (в

случае

присутствия кислорода

момент облучения)

до 1,5.

Если

же

кисло-

род подводили спустя

5 мс

после облучения,

то

величина

ККУ

уменьшалась

до 1,1. Для

получения.же максимальной сенсибилиза-

ции

этих опытах кислород надо было подавать

камеру

за 1-2 мс

до начала облучения.

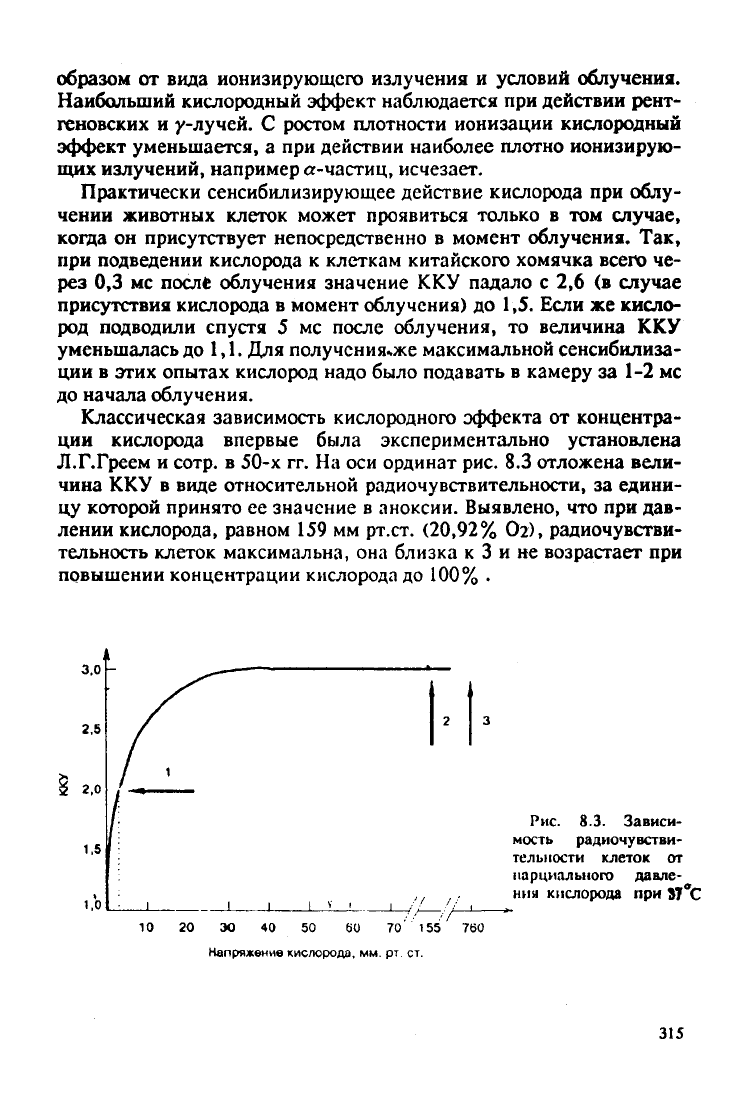
Классическая

зависимость кислородного эффекта

от

концентра-

ции

кислорода впервые была экспериментально установлена

Л.Г.Греем

сотр.

в 50-х гг. На оси

ординат рис.

8.3

отложена вели-

чина

ККУ

виде относительной радиочувствительности,

за

едини-

цу которой принято

ее

значение

аноксии. Выявлено,

что

при

дав-

лении

кислорода, равном

159 мм

рт.ст. (20,92%

Ог),

радиочувстви-

тельность клеток максимальна,

она

близка

к 3 и не

возрастает

при

повышении

концентрации кислорода

до 100% .

3,0

2.5

2,0

1.»

1,0

Рис.

8.3. Зависи-

мость радиочувстви-

тельности клеток от

парциального

давле-

ния кислорода при 5Т°С

20 30 40 50 60 70 155

Напряжение

кислорода, мм.

рт ст.

760

315

Кислородный

эффект находит применение в лучевой терапии:

повышение

содержания кислорода в опухоли и создание гипоксиче-

ских условий в окружающих тканях позволяют усиливать

лучевое

поражение опухолевых клетках с одновременным уменьшением по-

вреждения здоровых тканей.

Таким

образом, кислород - универсальный радиомодифицирую-

щий

агент.

Радиопротекторы и радиосенсибилизаторы

Область применения ионизирующих излучений в различных на-

правлениях науки и техники быстрыми темпами расширяется, что

выдвигает в качестве фундаментальной задачи современной радио-

биологии поиск путей повышения радиоустойчивости организма.

Одна из реальных возможностей решения этой задачи состоит в ис-

пользовании

средств фармако-химической защиты - протекторов,

существенно снижающих поражающее действие ионизирующей ра-

диации.

Проблема химической противолучевой защиты интенсивно

разрабатывается в лабораториях всего мира, большие успехи в этой

области достигнуты и в нашей стране (Ю.Б.Кудряшов, Е.Ф.Роман-

цев,

П.Г.Жеребченко, Е.Н.Гончаренко, А.С.Мозжухин, С.П.Ярмо-

ненко

и др.). Не менее активно разрабатывается и проблема, свя-

занная

с поиском средств, усиливающих

лучевое

поражение орга-

низмов

(А.М.Кузин,

Л.Х.Эйдус

и др.).

Радиопротекторы и радиосенсибилизаторы - вещества, введение

которых животному, а также добавление в культуральную

среду

или

к биологическому объекту перед действием ионизирующего из-

лучения вызывает соответственно значительное снижение или уси-

ление радиационного эффекта. Введение радиопротектора после об-

лучения организма неэффективно. Добавление радиозащитных

препаратов к биообъекту после его облучения может не дать долж-

ного эффекта. Показано, что введение цистеина после облучения

крыс

(не позже чем через 5 мин) оказывается неэффективным.

Защита

организма животных и биологических систем от поража-

ющего действия радиации с помощью химических веществ является

одним из наиболее значимых итогов развития радиационной био-

физики.

Радиопротекторы очень широко используются в целях по-

вышения

радиорезистентности организма и различных биологиче-

ских объектов. В век использования атомной энергии потребность в

химических протекторах никогда не отпадет, несмотря на огромные

возможности физической защиты.

316

Эффект

профилактической химической защиты организмов от

лучевого

поражения был открыт в 1949 г. 3.Баком.

настоящему времени из многих тысяч изученных соединений

отобраны наиболее эффективные, способные предотвратить гибель

животных, облученных в смертельных

дозах.

Некоторые радиопро-

текторы уже стали фармокопейными препаратами: их используют

при

лучевой терапии злокачественных новообразований.

Зная

механизм первичных физико-химических и биохимических

процессов,

развивающихся в организме после воздействия ионизи-

рующей радиации, можно нормализовать их при помощи опреде-

ленных радиопротекторов. С

другой

стороны, уменьшая эффект ра-

диационного

поражения путем введения ряда соединений, можно

понять

сущность процессов, происходящих в ткани в

результате

об-

лучения.

Защитные

вещества весьма разнообразны по своему химическо-

му строению и биологическому действию. Цианистый натрий был

одним из первых веществ, введение которого мышам в дозе 5 мг/кг

непосредственно перед облучением в летальных дозах повышало их

выживаемость по сравнению с контрольными животными

(З.Бак

сотр., 1949). Были изучены радиозащитные свойства и цистеина,

который

в дозе 1000 мг/кг значительно повышал выживаемость мы-

шей

(Г.Патт и сотр., 1949). Серосодержащие вещества - наиболее

многочисленная

и хорошо изученная группа защитных соединений.

Радиозащитным действием обладают азиды, аминокислоты, спир-

ты, сахара, фенолы, органические кислоты и т.д. Однако экспери-

ментальное изучение многих тысяч химических соединений выяви-

ло,

что наиболее перспективные и высокоэффективные из них от-

носятся

двум

классам веществ: индолилалкиламинам и меркапто-

алкиламинам.

Радиопротекторы, относящиеся к индолилалкилами-

нам,

являются производными триптамина. Последний при внутри-

брюшинном

введении мышам в дозах

79-95

мг/кг за 5-20 мин перед

облучением на

25-30%

повышал их выживаемость по сравнению с

контрольными

животными.

Одним из эффективных химических протекторов считается 5-ок-

ситриптамин

(серотонин):

— CH2NH2

317

Сейчас изучено более

двухсот

соединений, относящихся к классу

индолилалкиламинов, причем у некоторых из них выявлена проти-

волучевая активность, сравнимая с защитным эффектом серотони-

на.

Цистеинамин,

или 2-меркаптоэтиламин (МЭА)

обладает

способ-

ностью защищать животных от действия ионизирующей радиации в

летальной дозе. Обнаружение радиозащитной активности МЭА по-

служило толчком к интенсивному синтезу и

других

тиолсодержа-

щих соединений, в

результате

чего

были выявлены

другие

не менее

эффективные

радиопротекторы: меркаптопропиламин и его

дисуль-

фид,

аминоэтилизотиуроний, меркаптоэтилгуанидин, меркаптоп-

ропилгуанидин, аминоэтилтиофосфаты и многие

другие

вещества

класса меркаптоал

кил

аминов.

Различные гипотезы о механизмах противолучевой защиты так

или иначе связывают их с самыми начальными процессами, инду-

цируемыми в клетке при поглощении энергии ионизирующего из-

лучения.

Показана

значительная радиосенсибилизирующая эффектив-

ность (в отношении большого числа первичных

опухолей

мышей и

крыс) метронидазола, мизонидазола и

других

электроноакцептор-

ных соединений. При этом для достижения одного и

того

же

эффек-

та

требуются

дозы ионизирующего излучения почти в 2 раза мень-

шие,

чем при облучении без радиосенсибилизатора. В качестве ра-

диосенсибилизаторов применяют такие соединения, как синкавит,

иодацетамид, метилгидразин, иоддезоксиуридин и др. К эффектив-

ным

радиосенсибилизаторам относится и кислород.

Общие трудности использования радиопротекторов и радиосен-

сибилизаторов в радиоонкологической клинике состоят в значи-

тельной токсичности большинства препаратов, а также в необходи-

мости избирательности их действия на нормальные или

опухолевые

ткани.

Поэтому актуальной задачей клинической радиобиологии

является поиск условий, при которых поражение здоровых тканей

будет

минимальным, а

опухоли

- максимальным, а также выбор

средств и способов увеличения этой разницы.

6. Теоретические представления о механизме

биологического действия ионизирующих излучений

В последние два десятилетия четко выделились два направления

в развитии теоретических представлений о биологическом действии

радиации. Исследователи одного из них стремятся установить об-

щие,

в основном феноменологические, но обязательно количествен-

318

ные

закономерности, характеризующие начальные звенья

лучевого

поражения

клетки ("принципы попадания и мишени", "стохастиче-

ская

теория", "вероятностная модель радиационного поражения

клетки").

Другое

направление объединяет

ученых,

которые ставят

перед собой

задачу

объяснить все многообразие конкретных

луче-

вых реакций биологических объектов;

отсюда

преимущественно ка-

чественный, описательный характер гипотез данного направления

("гипотеза липидных радиотоксинов и цепных реакций",

"структур-

но-метаболическая теория").

Принцип

попадания и теория мишени

Теория

мишени - одна из количественных наиболее обоснован-

ных теорий биологического действия ионизирующих излучений,

летальный эффект которых имеет вероятностный характер

вследст-

вие случайного распределения элементарных актов первичного вза-

имодействия частиц с высокочувствительными объемами (мишеня-

ми) облученных объектов. Каждый акт одиночного переноса

энер-

гии

в теории мишени рассматривается как событие попадания, при-

водящее к поражению определенной биологической

структуры.

Ак-

ты попадания статистически распределяются по всей облучаемой

системе. При рассмотрении радиобиологических эффектов на моле-

кулярном и (или) клеточном уровне термин "мишень"

удобно

ис-

пользовать для формального обозначения

того

микрообъема, в ко-

тором должны произойти одна или несколько ионизации, приводя-

щих к наблюдаемой (изучаемой) реакции. В зависимости от числа

попаданий,

необходимых для поражения, различают одно-, дву- и

многоударные объекты или реакции.

Принцип

попадания и принцип мишени (чувствительной обла-

сти) и основанная на них теория мишени получили развитие в тру-

дах Д.Кроузера, Н.В.Тимофеева-Рсссовского, К.Циммера, Д.Ли,

исходящих в своих теоретических представлениях о механизме би-

ологического действия ионизирующих излучений из статистики

(уравнения) Пуассона.

Представим, что облучаемая биосистема состоит из No объектов,

каждый из которых имеет мишень сечением S. Пусть для инактива-

ции

объекта достаточно, чтобы трек плотноионизирующей частицы

прошел через сечение мишени S, т.е. произошло попадание. Если

траектории частиц распределяются по поперечному сечению объек-

та случайным образом и не зависят

друг

от

друга,

то вероятность

(Рп)

одного,

двух,

..., п попаданий в мишень, находящуюся в преде-

лах объекта, описывается уравнением:

319

P(n)-a

• e~

/n!, (8.1)

где a - среднее число попаданий в мишень; п! - n-факториал. Обоз-

начим

через D среднее число частиц, пролетающих через единич-

ную площадку сечением S,

тогда

a - SD. (8.2)

При

какой угодно малой дозе облучения D

существует

вероят-

ность прохождения частицы через одну из мишеней. С ростом дозы

облучения увеличится число мишеней, претерпевающих попада-

ние.

Ясно, что при возрастании размера мишени повысится и веро-

ятность попадания. Если принять за No общее число объектов в об-

лучаемой системе, а за N - число объектдв, сохранивших после об-

лучения исходные свойства (т.е. "выживших"), то величина N/No

соответствует вероятности непопадания

(п=0).

Из уравнения (8.1)

для случая п=0 получим

N/No

- (SD)° •

/0!

= e"

, (8.3)

так

какО!=1.

При

некоторой дозе облучения выполняется условие SD-1; это

соответствует случаю, когда в среднем число попаданий равно чис-

лу мишеней. В действительности же часть попаданий испытали уже

однажды пораженные мишени, а некоторые не претерпели ни одно-

го попадания. Согласно статистике Пуассона при SD=1 реально по-

ражается только 63% мишеней, 37% их оказываются непоражен-

ными.

Подтверждение этому можно получить, если подставить в

уравнение (б.3)значение

SD=1,

тогда

N/No-е^-е"

=0,37.

Отношение N/No, определяемое экспериментально, представля-

ет собой долю "выживших" объектов по отношению к их общему

числу до облучения. Найдя

дозу

облучения, при которой выживает

37% объектов (D37). можно рассчитать сечение мишени:

SD37-I или5=1/Оз7.

На

рис. 8.4, А-В представлена схема, иллюстрирующая зависи-

мость числа пораженных мишеней от дозы облучения. Видно, что

даже

при малой дозе облучения некоторое число частиц проходит

через мишени и вызывает их инактивацию; увеличение дозы

облу-

чения

приводит к резкому (почти по линейной зависимости) возра-

станию числа.пораженных объектов, а затем вес более вероятно по-

вторное прохождение частиц через однажды пораженные мишени.

При

дозе D37 общее число частиц соответствует числу мишеней

(SD=1),

однако 37% объектов остаются непораженными, так как

320