Аракелян А.К., Афанасьев А.А. Вентильные электрические машины в системах регулируемых электроприводов. Том 2

Подождите немного. Документ загружается.

227

226

где













экв

тэкв













TTTapTTTTapTaRa









22332

пт

pTpTpEab





- постоянные коэффициенты,

определяемые параметрами ВД и регулятора тока.

Решим (17.37) совместно с третьим уравнением системы

(17.31). Вычислив частный определитель, выведем

эc

по

возмущающему воздействию на двигатель. Определив модуль

 

 

pэкв

pэквэквт

эc



































TTTTa

(17.38)

и подставив значения резонансных частот демпфированных

колебаний

pII



pIII



для заданных



экв

, получим расчетные

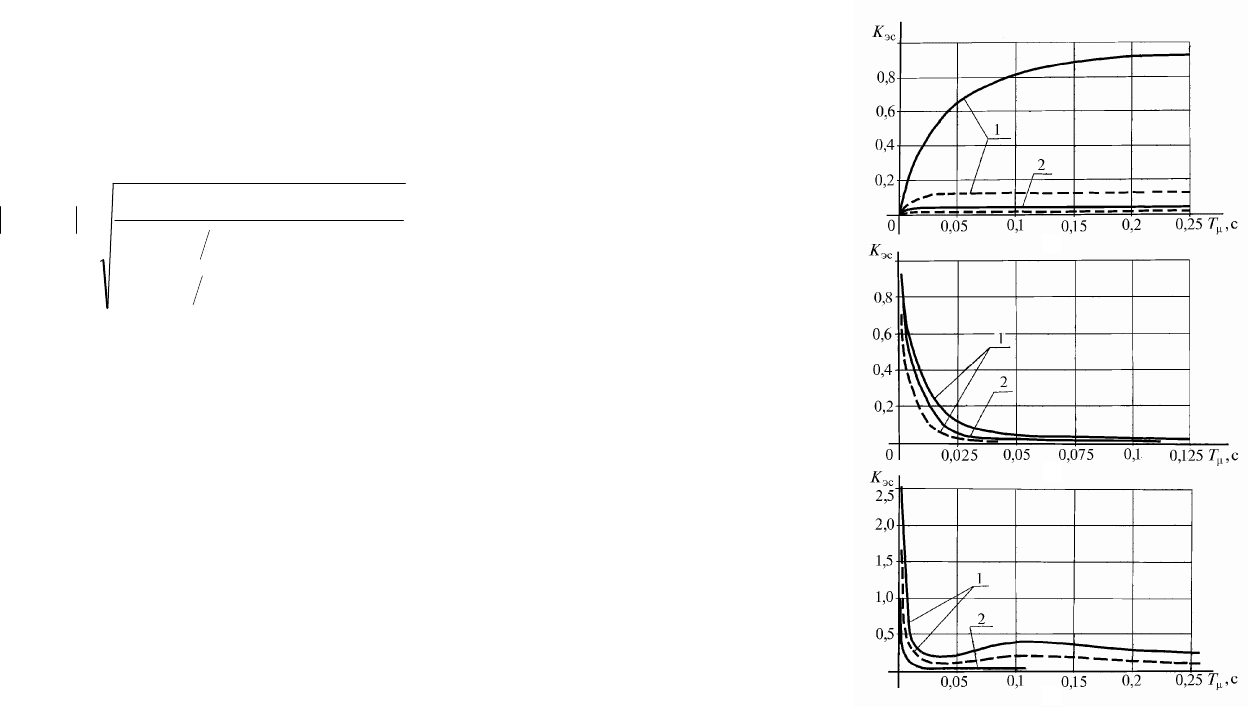
(рис.17.8, а).

При малых частотах (рис.17.8,а), т. е. в области возмущений,

где в разомкнутой САР имеет место интенсивное демпфирование

колебаний электроприводом (табл. 17.3), электромеханическая

связь значительно ослабляется при сравнительно малых значениях

некомпенсированной постоянной



. При

01,0





с и при егоо

увеличении демпфирующая способность ВД возрастает. Это

противоречит полученному (рис.17.7,в) результату, в САР с ИТ-СД

оптимизация контура тока приводит к замене звена (якоря ВД) с

большой инерционностью интегрирующим звеном с еще большей

постоянной времени. Для обеспечения оптимального

быстродействия по общепринятым критериям качества переходных

процессов при пуске САР с ВД необходима форсировка напряжения

якоря ВД, что достигается подбором (расчетом) относительно

меньшего значения некомпенсированной постоянной.

Оценим электромеханическую связь САР ДЭМС с ВД с

оптимизированным контуром скорости, реализуемым с помощью

тахогенератора, установленного на стороне электропривода.

Передаточная функция регулятора скорости для однократно

интегрирующей САР [388]

Рис. 17.8. Коэффициент электромеханической связи (

эc

) в

оптимизированной по быстродействию системе: а - при регулировании

тока якоря в функции малого параметра (



); б - при статическом

регулировании скорости двигателя в функции (



); в - то же при

астатическом регулировании скорости: 1 -

с;1,0

экв

T

2 - ;с175,0

экв

T

––––––

IIр



; - - - - -

рIII



229

228

Расчетные кривые

)(

эc 

(рис.17.8,б) показывают, чтоо

астатическая САР с ВД на базе типового СД также обладает

значительной электромеханической связью. Однако эта связь

несколько ниже, чем в аналогичной САР с ДПТ, из-за сравнительно

высокого значения эквивалентной электромагнитной постоянной

якорной цепи ВД.

Следовательно, если при синтезе САР с ВД для ДЭМС с

большой податливостью механического звена целесообразно

статическое регулирование скорости или токоограничивающей

характеристики с невысокой степенью точности, то в ДЭМС со

слабодемпфирующим механическим звеном желательно

астатическое регулирование скорости или момента.

В первом случае условия для демпфирования упругих

механических колебаний электрической частью и возникшие

колебания электропривода от управляющих воздействий

благоприятны, поэтому специальные меры по обеспечению

демпфирования сводятся к оптимизации регуляторов [501]. При

относительно малых



(меньших 0,01 с) возникают условия,

характерные для САР с жесткой электромеханической связью, в

которой демпфирование ослаблено вследствие чрезмерно жестких

механических характеристик ВД. Механические колебания в этом

случае не вызывают изменений скорости электропривода и отвода

энергии колебаний в якорную цепь, поэтому следует параметры

регуляторов подбирать такими, чтобы сумма некомпенсированных

постоянных САР была не меньше 0,01 с.

Выводы

1. Многомассовые электромеханические САР с ВД на базе

типовых СД в линейном приближении обладают большим диапазоном

возможных значений коэффициента электромеханической связи, в

каждом конкретном случае этот коэффициент может быть

рассчитан.

2. Область слабого демпфирования, как правило, охватывает

верхний диапазон регулирования, включая и критическую скорость

приводного двигателя, поэтому САР МЭМС с ВД по

быстродействию может быть оптимизирована на основе

 

pTaaRK

KTK





cnэквjc

еомот

рc

, (17.39)

где а

- коэффициент, характеризующий демпфирование контура ско-

рости.

Пренебрегая внутренней связью ВД по ЭДС с членом второго

порядка оптимизированного замкнутого токового контура, получим

уравнение контура регулирования скорости:

 

 

 

pTTTaK

pWK 







эквмтот

0п

рcоc

Преобразование этого уравнения по известному методу дает

выражение комплексного коэффициента электромеханической

связи. Выделив модуль

эc

, имеем:

 

экв

01тc

эc









TTTa

TTaa

Расчетные кривые

)(

эc 

(рис.17.8,б) показывают, что при

малых



существенно возрастает

)(

эc 

по сравнению с

эc

которое было получено с учетом значений, соизмеримых с

(рис.17.7,а). Это свидетельствует о том, что, как и для САР с

ДПТ или АД [429], уровень статизма регулировочных

характеристик ВД играет существенную роль в приобретении

определенных демпфирующих свойств.

Рассмотрим двукратно интегрирующую систему, т. е. астатиче-

скую систему регулирования. Учтем и внутреннюю обратную связь

ВД по ЭДС вращения [32]:













 

. 1

эквэкв10п

пртрc1оc







pTRppE

pTKpWpWpK

(17.40)

Решая (17.40) совместно с уравнением моментов из (17.31),

определим комплексный коэффициент







эc

, модуль которого будет

 





 

 

 



























1111

тc

01экв

тc

01тc

эc

TTT

TaaTTTaaTa

TTaa

. (17.41)

231

230









cот

*-1

123

1 



 MKTMTJJc

ММ

;

 Mc

;





эквувхмо





 MRKUKM

;





 SM

;



мН105,14



;

0схеомо

fad

ILKPKK





;

эквуотот

RKKK





;

-1

эквэквэкв

RLT 

;

ядэкв

LLL 

 





; 2cos33

















qdqd

LLLLL





;

дэкв











qdd

LLLrrR

;

-2

моэкв

KRJT

М 



;

1* 



 MMM

;

sin

































 tgMM

;0,3

L

;7636,1



aqad

;1178,0





;8814,1



;0001,0

r

;1698,0









LL ;0069,0

r

;23

сх



K

60,30





фи0п

36000



UE

В;

314





рад/с;



p (число пар полюсов СТД).

17.4. Синтез систем автоматического регулирования

с вентильным двигателем

Приведем математическое описание электромагнитных

процессов вентильного двигателя в неподвижной системе координат

и получим структурную схему, пригодную для анализа и синтеза

систем автоматического регулирования электропривода [32, 28]

Математическое описание электромагнитных процессов

выполним исходя из общеизвестных допущений, отмеченных в 17.1.

Для вентильного двигателя, бесконтактный коммутатор

которого выполнен по схеме инвертора тока [20], в качестве

переменных удобно принять токи отдельных контуров, тогда

система известных уравнений напряжений и потокосцеплений

примет вид

приведенного жесткого (одномассового) механического звена (т.е.



экв12

) известными методами.

3. Область существенной электромеханической связи в этих

САР охватывает область низкочастотного главного колебания,

поэтому передаточные функции регуляторов при последовательной

либо параллельной коррекции и место установки тахогенератора

рассчитаны и могут быть выбраны, например, по [429, 501, 532].

Приложение 17.4

Синхронный турбодвигатель 4000кВт;СТД



= 3000 об/мин;

мкг278 GD

;

15,0



м,

56,2



м. Питательный насос

кВт,3200ПЭН



мкг0,21 GD

(при рециркуляции), GD

= 54,0 кг

(при подаче),

11,0



м,

6,1



м. Тахогенераторор

ТГ-180П,

232

мкг102,1 



, зубчатая соединительная муфта -

мкг0,1 GD

мН10318,0

C

мН10288,5

3423

 CC

с13,251





с1321





(без жидкости),

с1610





(с жидкостью),

эквМп

TTT

a 

;

 

;

пэкв

2 М

TTT

a 













эквотп

-1

01эквп

-1

1213

TKTTJJTTTJJJa

ММ



;









01эквп

-1

1214

 TTTJJJa

;









01эквп

215





TTJJJa

;

010

а

;





*-1

121

MMTJJb



;

-1

122

MJJb 

;









cп

*-1

1213

MTMTJJJb



;

 Mb

;

cэквп

-1

121

 MTTTJJc

;





cэквп

-1

122

 MTTTJJc

;

Базовыми являются общепринятые номинальные параметры СД.

233

232

(17.42)

где



- угловая скорость вращения гладкой составляющей

магнитного поля ВД.

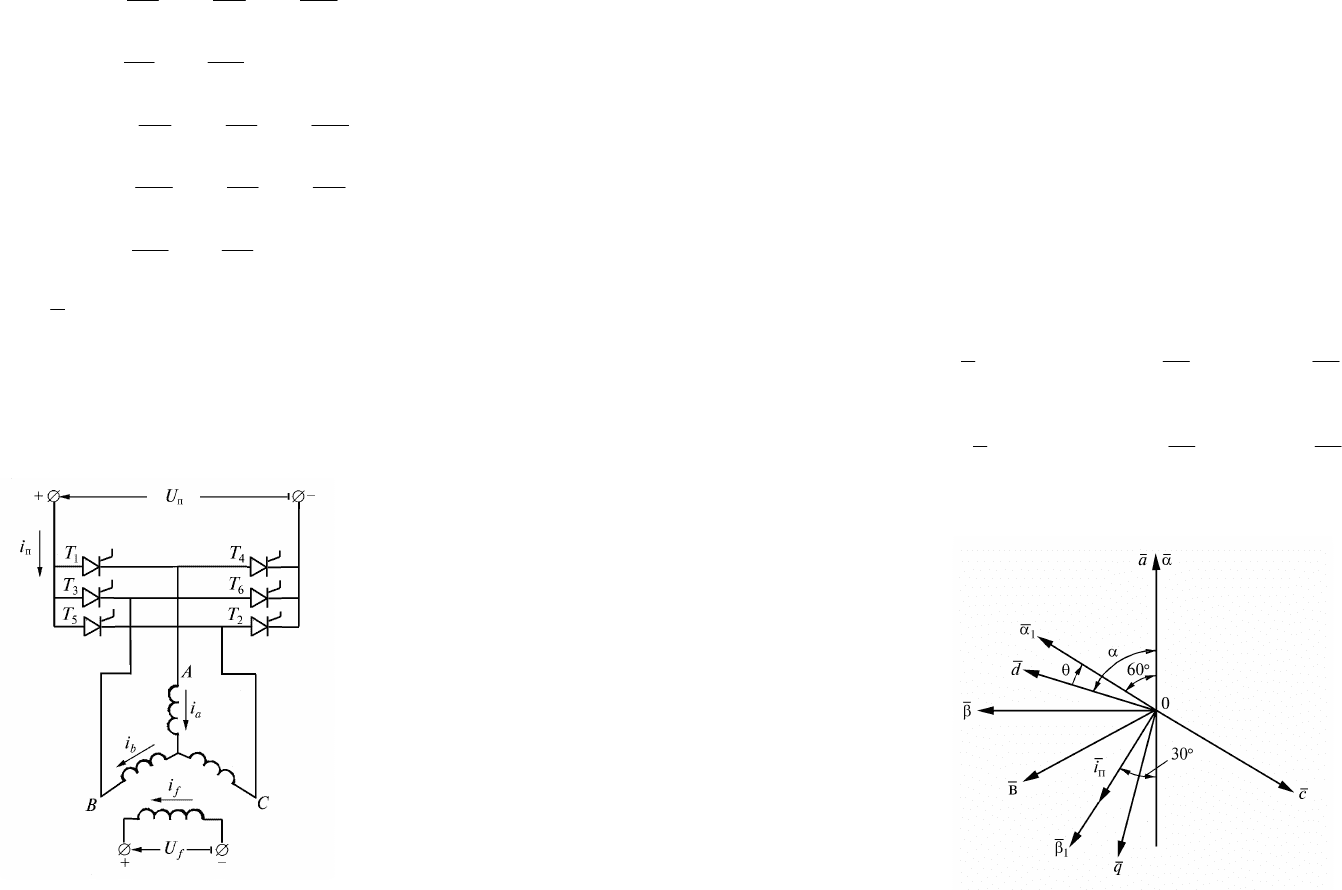
Анализ электромагнитных процессов проведем с учетом

дискретности вентильной части системы (рис.17.9).

Рассмотрим межком-

мутационный период.

Допустим, что проводят ток

тиристоры Т

, Т

, тогда















;

(17.43)

где

- мгновенное значение

входного тока инвертора.

Взаимное положение в

пространстве осей ротора и

статора будем

характеризовать углом



(рис.17.10).

В начальный момент

р а с с м а т р и в а е м о г о

межкоммутационного периода для угла



справедливо равенствоо

0нач

30 



где



- угол коммутации;



- начальный угол управления

инвертором, задаваемый датчиком положения ротора.

За время межкоммутационного периода ротор поворачивается

на угол





и к концу межкоммутационного периода угол



принимает значение

.90

0кон





Воспользовавшись формулами преобразования, осуществим

переход к неподвижной системе координат для переменных статора:

;

cos

coscos













































cвad

iiii

sin

sinsin













































cвaq

iiii

Подставив в эти равенства соотношения (17.43) и выполнив

Рис.17.10. К определению пространственного положения осей статора

и ротора

Рис.17.9. Упрощенная силовая

схема вентильного двигателя

 

   

 





















;

dkqaqqkdfadqdqd

kqkqkq

kdkdkd

ffff

kdadddfad

qqq

kqaqqq

ddd

iiLiiiLiiLLpM

Lir

LirU

iLiLiL

LriU

iLiL

LriU



235

234

преобразования, получим













.cos

;sin

(17.44)

Здесь введено обозначение текущего угла:





Мгновенные значения фазных напряжений













































sin

cos

;sincos

qdв

qda

UUU

(17.45)

Напряжение, подводимое к инвертору:





UUU





Подставив в это уравнение соотношения (17.45) и выполнив

преобразования, получим





. cossin3



UUU

(17.46)

Принимаем неподвижную систему координат





(рис.17.10),

одна из осей которой совпадает с результирующим вектором тока

якоря

. В этой системе координат взаимное положение в

пространстве осей ротора и вектора результирующего тока якоря

характеризуется углом



. За положительное направление

отсчета угловых положений принято направление, совпадающее с

угловой скоростью ротора. В этой системе координат ротор

принимается неподвижным, тогда результирующий вектор тока

якоря

перемещается относительно ротора со скоростью



обратным знаком.

В неподвижной системе координат дифференциальные

уравнения для контуров ротора из (17.42) принимают вид























.sin

cos

;cos

sin

;cos

sin

1п

•

Lir

LiL

Lir

LiL

LirU

kqkqkq

adad

kdkdkd

adad

ffff

Решая данную систему уравнений относительно производных,

получим

;cos

sin

1п

kdkd





;sin

cos

1п

 i

kqkq

 

. cos

sin

1п

















































adfff

kdkdf

LriU

LLL

(17.47)

Уравнение электромагнитного момента из (17.36) и уравнение

(17.46) с учетом (17.42), (17.44) и (17.47) принимают соответственно

вид

237

236





  

.sinctg1

3costg

sin2

3cos

sin22

п1п















































































































































kqkq

kdkd

fff

kqaqkdad

dfad

riU

iLiL

LiL

LirU

(17.48)





 

. sincos

32sincos3

пп





iiLiiL

piLLpiiLpM

kqaqkdad

qdfad

(17.49)

Уравнение (17.48) после преобразований можно представить в

виде

 



,sin

3cos3

2sincos322



















ctg

Шпп

kqkdkqkdkd

kdf

fff

kdf

kqaqkdad

afad

irkir

riU

iLiL

LriU

(17.50)

где

 

















 2cos

dqqd

LLLL

- индуктивность якоря дви-

гателя, абсолютное значение которой зависит от углового положе-

ния ротора;

;

k 

;

k 

k  - коэффициенты связи обмоткитки

возбуждения и демпферных контуров по осям d и q.

Индуктивность реакции якоря определяется по формуле









dqqda

LLLLL













или

 



























kdf

fkdkdf

adqda

kkkk

LLLL

При анализе и синтезе САР, которая выполнена по принципу

подчиненного регулирования, будем пренебрегать пульсациями

момента и скорости, обусловленными дискретностью переключения

тока в фазах якоря. Кроме того, будем полагать, что коммутация

тиристоров инвертора идеальная.

С учетом этих допущений осуществим переход в (17.49) и

(17.50) к средним значениям:

 



















,2sin

cos

;22

п0п

дв

•

япп

LLpk

iiL

LriU

qdcx

fad

(17.51)

где

 

0я

2cos





















dqqd

LLLL

- среднее значение ин-

дуктивности якоря при заданном угле



;

дв

- среднее значение выпрямленной ЭДС вентильногоо

двигателя;





233

- коэффициент схемы выпрямления для трехфаз-

ного мостового инвертора;

239

238

 

0п0п

sincos

 iiLiiLp

kqaqkdad

- составляющая

электромагнитного момента, обусловленная действием

демпферных контуров.

Для электрических машин с демпферной обмоткой можно

пользоваться упрощенной формулой при нахождении индуктивности

якоря:









Среднее значение выпрямленной ЭДС вентильного двигателя

можно представить в виде суммы отдельных составляющих:

тврa0дв

eeeee









;

010

cos



fad

;

01па

2sin

 iL

;

 

100вр

sincos



kdadkdad

iLiL

;





 





 



,sinctg

















kqkqkq

kdf

kdkdf

kdfff

kdf

irk

kriU

где

- ЭДС холостого хода;

- ЭДС реакции якоря;

вр



- ЭДС вращения, обусловленная действием демпферной

обмотки;

- трансформаторная ЭДС.

Если полученные соотношения дополнить уравнением

движения и учесть, что напряжение к вентильному двигателю

подводится от управляемого выпрямителя, то будем иметь систему

дифференциальных уравнений, пригодную для анализа

электромеханических процессов:

 

























;2sin

cos

;

cossin

п0п

твр

00п

эпэв

JMM

iiL

iLiL

LiRe

fad

afad

(17.52)

где

- среднее значение ЭДС выпрямителя;





рдтэ

rrrR

- эквивалентное сопротивление якорной

цепи с учетом сопротивления трансформатора (

), сглажи-

вающего дросселя (

) и эквивалентного сопротивления, учиты-

вающего коммутацию управляемого выпрямителя













2

;

дтяэ

2 LLLL 

- эквивалентная индуктивность якорной це-

пи с учетом индуктивности трансформатора (

) и

сглаживающего дросселя (

);



- угловая скорость вращения ротора.

Приведем (17.52) к операторной форме записи:

















       

   

     

























;2sin

cos

;2sin

cos1

п0м

твр0п

0епээв

pJppMpM

pMpi

LLpk

picpM

pepeppiL

pcpipTRpe

qdcx

(17.53)

241

240

где

- коэффициенты ЭДС, холостого хода и электромагнитно-

го момента,

fad

ем



;

- электромагнитная постоянная времени якорной цепи,

T 

Таким образом, получена система дифференциальных

уравнений, по своей физической сущности близкая к

электроприводам с машинами постоянного тока, методика анализа

и синтеза которых достаточно разработана. На основании

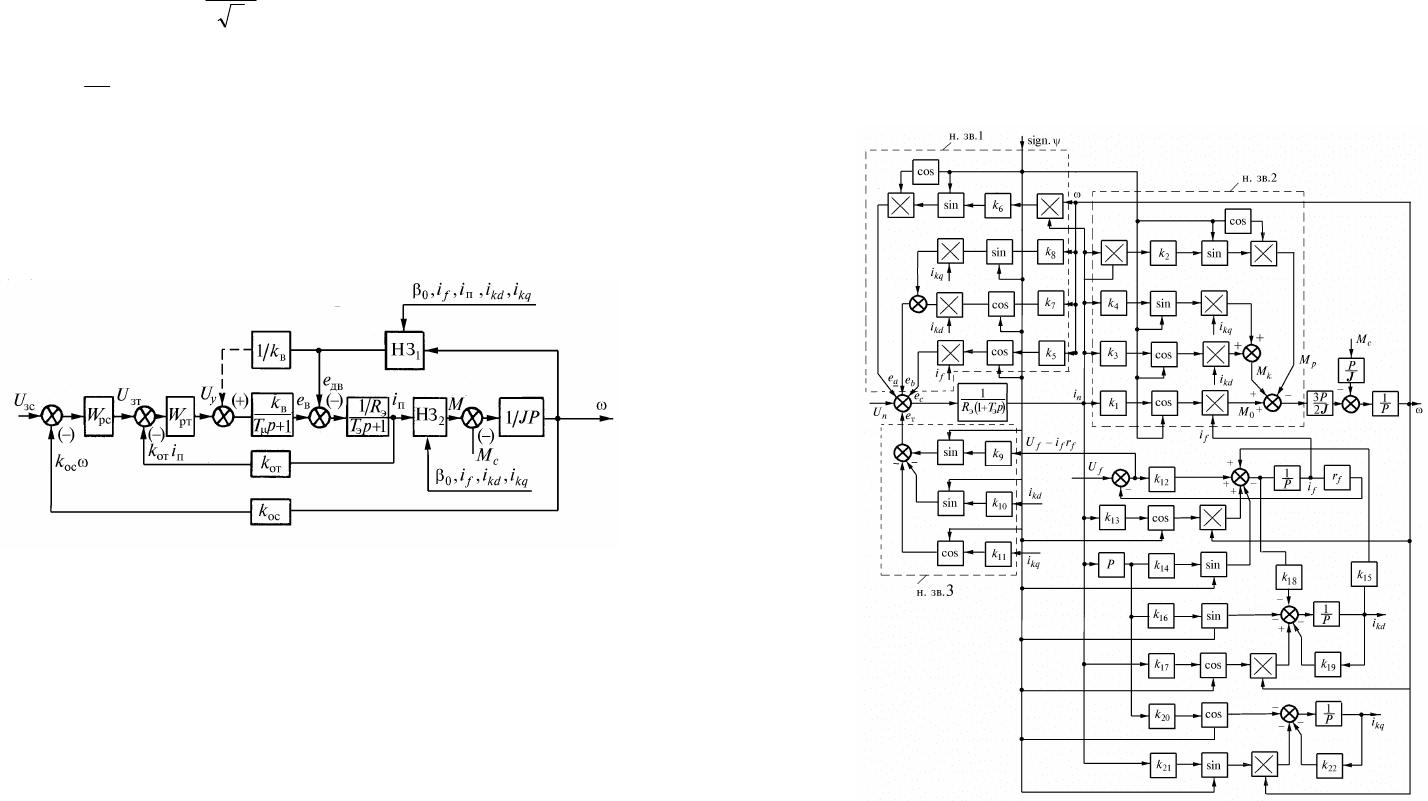
полученных соотношений строится двухконтурная система

подчиненного регулирования (рис.17.11).

В приведенной схеме управляемый выпрямитель представлен

в виде линейного звена с коэффициентом усиления

и фильтромм

на входе с малой постоянной времени



В исходной структурной схеме по модели рис.17.12 можно

выделить четыре звена: звено тока якоря

, звено тока обмотки

возбуждения



и звенья токов демпферной обмотки

В этой модели отсутствуют сильные перекрестные частотно-

зависимые связи между напряжением и ЭДС контуров якоря, а

собственные связи контуров обмоток ротора слабодействующие,

поскольку контурные коэффициенты

из-за

малых постоянных

проявляют себя в динамике

пренебрежимо слабо (см. прил. 17.5).

Рис.17.11. Структурная схема САР

Рис.17.12. Модель структурной схемы вентильного двигателя

в осях





, - неподвижных в пространстве: Т

- эквивалентная

электромагнитная постоянная входной цепи инвертора

Сильнодействующие связи между якорной обмоткой, обмоткой

возбуждения и демпферной обмоткой ротора особо проявляют себя

в динамике по аналогии с некомпенсированным двигателем

постоянного тока. Однако при малых установочных углах ДПР

(следовательно, при малых

sin



) влияние этих связей, как

показывает опыт, пренебрежимо мало. Поэтому с целью упрощения

и иллюстрации наглядности дальнейший анализ и синтез САР с ВД

243

242

в неподвижной системе отсчета ведется только по цепи якоря в

предположении, что компенсация реакции якоря осуществляется

автоматически путем компаундирования возбуждения входным

током инвертора, а действия нелинейных составляющих ЭДС и

электромагнитного момента в канале якоря ВД выражаются

реакциями нелинейных звеньев НЗ1 и НЗ2, вводимых в структуру

ВД. В вентильном двигателе в значительной мере проявляет себя

внутренняя обратная связь по ЭДС двигателя. Наиболее ярко это

наблюдается при реверсировании, когда изменяется угол управления

инвертором



. В связи с этим при оптимизации контура регулирова-

ния тока необходимо принимать меры по компенсации влияния внут-

ренней обратной связи по ЭДС двигателя.

Непосредственное измерение ЭДС вентильного двигателя

затруднено, поэтому целесообразно воспользоваться косвенными

методами. Довольно простое решение вопроса компенсации

внутренней обратной связи по ЭДС предложено в [165].

Воспользовавшись этой методикой, определим передаточную

функцию регулятора тока:

 

ээ

отв

рт

pTa







Напряжение задания по току

зт

подается с выхода фильтра,

имеющего передаточную функцию:

 







pTa

где





TTa

тт

- коэффициент, характеризующий степень демпфи-

рования колебаний тока;

- постоянная интегрирования контура

тока.

Передаточная функция оптимизированного замкнутого

токового контура

 

от

зам







pTTaTpTa

Расчет контура скорости осуществляется известными

методами. Нелинейное звено НЗ2 удобно представить в виде

упрощенной передаточной функции

 





 

,cos

0м

нз2

 c

которая может быть получена из (17.51) при пренебрежении

реактивной составляющей электромагнитного момента и

дополнительным моментом, вызванным действием демпферных

контуров (рис.17.12).

При определении передаточной функции регулятора скорости

следует принимать во внимание законы регулирования тока

возбуждения и угла управления инвертором.

Если скорость регулируется при поддержании постоянной

составляющей результирующего магнитного потока, действующего

перпендикулярно обобщенному вектору тока якоря, то

const,cos

м00м





где

0м0

fad

c 

- коэффициент электромагнитного момента,

пропорциональный нормальной составляющей магнитного потока;

- ток возбуждения двигателя при холостом ходе.

Для однократно интегрирующей системы передаточная

функция регулятора скорости принимает вид

 

тсэос

ме0от

ср

pTaaRk

Тсk





где

сомо

Т 

- электромеханическая постоянная времени;

- коэффициент, характеризующий демпфирование для конту-

ра скорости.

Для оптимизированной САР (рис.17.13) было проведено

исследование переходных процессов на аналоговой модели

(рис.17.14).

Проведенные исследования на аналоговой модели и

экспериментальной установке показали удовлетворительное

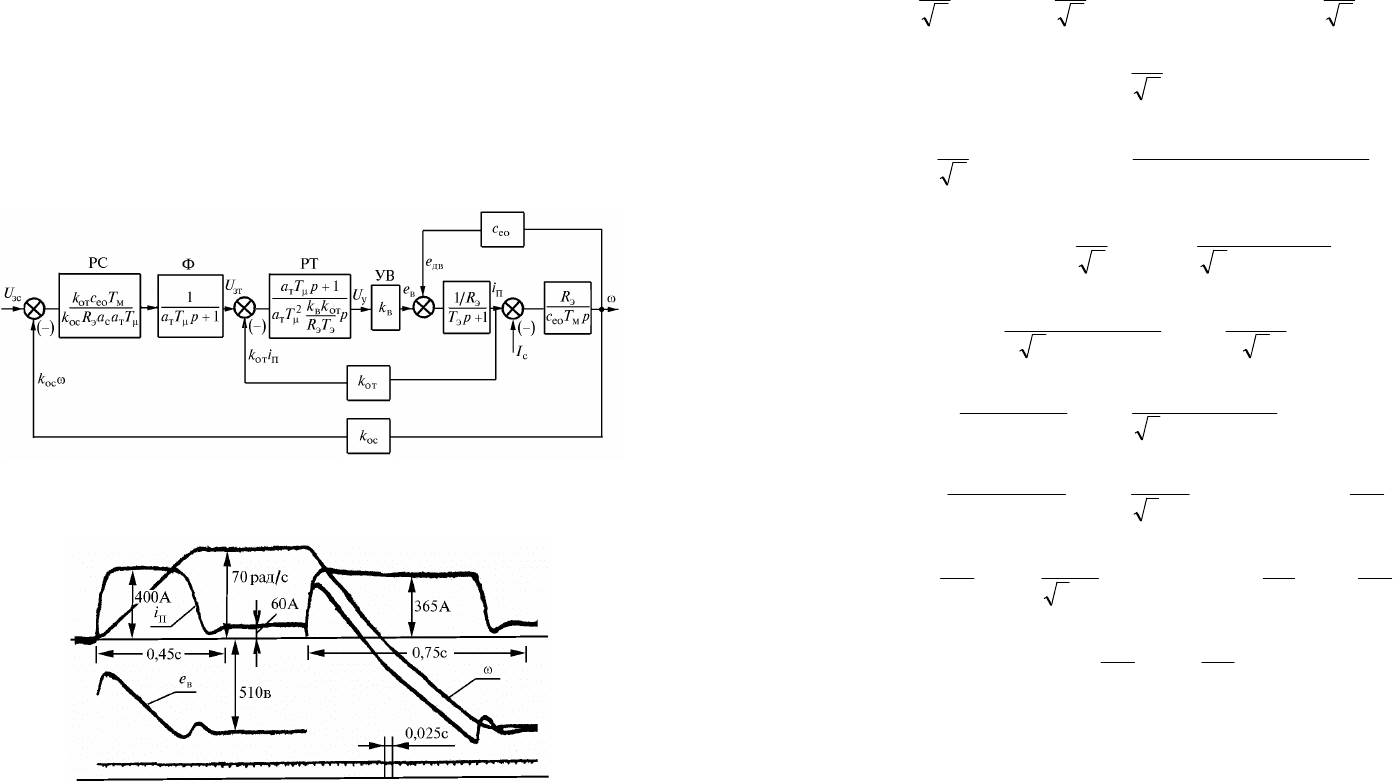
245

244

качество переходных процессов. Полученные соотношения были

использованы при разработке экспериментального электропривода

питательного насоса [28] (прил. 17.5).

Конструирование и синтез САР электропривода с ВД для

реализации режима пуска при условии задания алгоритма

переключения вентилей инвертора рассмотрены выше (см. гл. 7).

Расчет же параметров регулятора тока якоря ВД с учетом

прерывистости тока во входной цепи инвертора представляет

частный случай, требующий построения адаптивного регулятора

тока.

Рис.17.13. Упрощенная структурная схема САP

Рис.17.14. Осциллограмма переходных процессов пуска и реверсирования

двигателя

Приложение 17.5

Постоянные коэффициенты схемы рис. 17.11.

 

;

; ;

;

41321 aq

KKKLLP

KPL

K 

;

5 ad

K 

 

;

)1()1(







































kdf

fkdkdf

adqd

KKKK

LLL

 

;

)1(

;

9857

kdf

kdfcx

KKk

KKK





 

;

)1(

1110 kq

kqcx

kdf

fkdkdcx

KrKk

K 









 

; ;

;

1314

LLL

adkdf

adkdad

adkdf











 

; ; ;

;

18161716

adkdf

kdad

KKK

LLL

K 





; ; ; ;

;

2220212019

KKK

K 

; ;

K 

где

kqkdf

KKK , ,

- коэффициенты связи обмотки возбуждения и

демпферных контуров ротора по осям d и q.