Аракелян А.К., Афанасьев А.А. Вентильные электрические машины в системах регулируемых электроприводов. Том 2

Подождите немного. Документ загружается.

187

186



































;

к55

к56к555453

к44

к46к454443

к36ђ353433

26к25к2423

2221‰пк26

к25242322

16к15к1413

1211впк16

к15141312

qdf

ipaipaipapapa

Uib

ipaipaipapapa

bibibib

bbUMUipa

ipaipapapapa

bibibib

bbUMUipa

ipaipapapapa

(17.3)

где

- постоянные коэффициенты, 3,2,1 ...,3,2,1



ji :

 

 

 

; ,

tg2sin

cos

2sin23

100э

ILLMp

mqd



































 

 

 



 



 

; ,

sincos

cos

cos33

2sin23

1001

100э

mqd

ILLMp

































. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

; ,cos

cos

cBb











. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2616

 bb

при

0с0э



;

J - момент инерции ротора электродвигателя и присоединенных

вращающихся масс.

Представим полученные в (17.3) дифференциальные уравнения

в операторной форме по Лапласу для приращений выходных величин

в функции входных величин с учетом внешнего возмущающего

воздействия:

 

 

 

   

 

 





















































pWpU

ijf

(17.4)

где

 

 









 





- матрица передаточной функции ВД для

входных (управляющих) воздействий;





pQ - определитель системы (17.3),

 

5554535251

4544434241

3534333231

2524232221

1514131211



AAAAA

(17.5)









- транспонированная матрица;





- алгебраическое дополнение определителя





pQ ;

- операторные коэффициенты,

; ,

1112

1111

cBbpapaA 

. . . . . . . . . . . . . . . . . . . . . .

; ,

555655

cBbpaA







.1 ;2;5 ;5,...1,



lnmji

189

188

Решая (17.4) с учетом (17.5), получим:





























             

















;

52п

51к

42п

41к

32п

22п

12п

pMpWpUpWpUpWpi

pMpWpUpWpUpWp

(17.6)

где





- передаточные функции ВД соответственно по

управляющим и возмущающим воздействиям,

;5,...1



3,...1



j .

Выражения по (17.6) позволяют определить передаточные

функции и вычислить необходимые частотные характеристики ВД

при любом характере воздействия на САР, однако практическое

использование этих уравнений связано с громоздкими

вычислительными операциями. Существенное упрощение структуры

ВД можно получить при тактовой синхронизации инвертора по

положению ротора двигателя (

const





) либо при синхронизации

по напряжению якоря (

const





) и использовании средств

искусственной коммутации, позволяющих свести к минимуму

пространственный угол между вектором реакции якоря и поперечной

осью ротора. Так, например, при соответствующей установке

датчика положения ротора (





), обеспечивающего холостой ходд

двигателя практически при

0 ,0





, все динамические

процессы ВД оказываются связанными с поперечной осью магнитной

системы машины. Следовательно, можно допустить:

.0 ;0

;





dqqq

fadfd

Результаты анализа при таком допущении, как отмечается для

ВД с

const





в гл. 5, могут оказаться приемлемыми также для

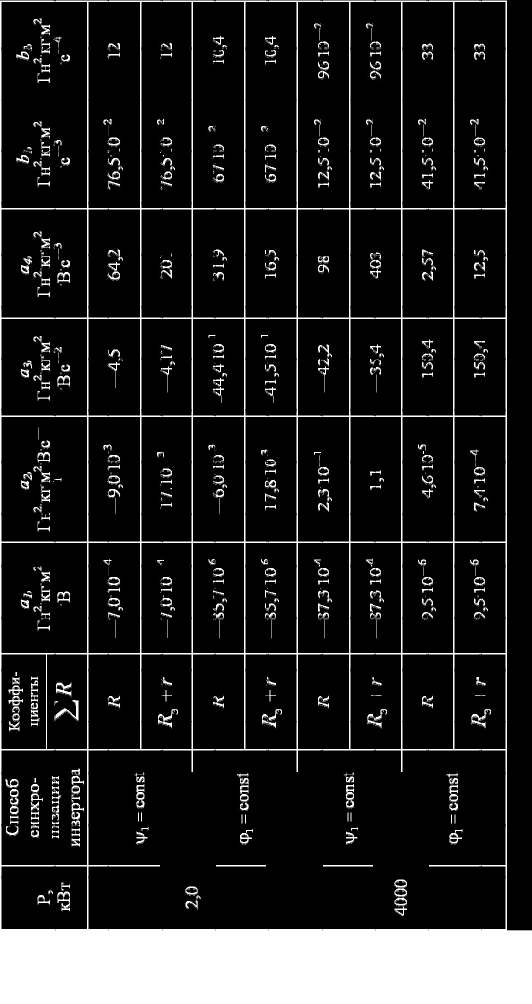
случая нагруженного двигателя, структурно представленного на

рис.17.2 для ВД с

const





Передаточная функция этой структурной схемы, например по

управляющему воздействию









для приращения скорости,

определится из (17.6):













pWPUp

11п



, (17.7)

где

 

apapapa

bpb







;









; cos02









LKrTJrTa













; coscos022

00э2













LrRTTKrJra

















; 03cos202

222

0э3 qfad

TILpKrRJJrKra 













; cos03

0э

 rRKrILa

fad





;cos03



qfad

TrILrb





.cos03



fad

ILrb

При тактовой синхронизации инвертора по условию

const



коэф-

фициент





 K

cos

, указанный на структурной схеме, заменяется на

021

 kk

Рис.17.2. Упрощенная структурная схема вентильного двигателя:

эквивалентное сопротивление, учитывающее сопротивление

сглаживающего дросселя и коммутационного явления в инверторе,

нf



приведенный к обмотке статора номинальный ток возбуждения

двигателя

191

190

Анализ уравнения (17.7) показывает, что коэффициенты

характеристического уравнения при использовании инверторов тока

(со сравнительно большой индуктивностью во входной цепи) могут

иметь различные знаки, что при отсутствии регуляторов

возбуждения или напряжения (или и того, и другого) обусловит

неустойчивую работу [46].

В целях сопоставления ожидаемых результатов при

исследовании модели ВД по рис.17.2 с синхронными двигателями

соответственно 2,0 и 4000 кВт (см. прил. 17.1) при различных

способах синхронизации инвертора и различных величинах

сопротивлений входной цепи были рассчитаны коэффициенты

характеристического уравнения (17.7) и операторного коэффициента

управляющего воздействия, которые сведены в табл.17.1.

Данные таблицы свидетельствуют о существенном влиянии

на степень устойчивости ВД индуктивности сглаживающего

дросселя и суммарного активного сопротивления цепи постоянного

тока, частично учитывающего влияние коммутационного процесса

в системе инвертор-двигатель.

Таким образом, по линеаризованным уравнениям синхронной

машины получены сравнительно точные передаточные функции

ВД, по которым можно произвести построение частотных

характеристик ВД при синтезе САР. Упрощение структуры ВД

позволяет снизить порядок характеристического уравнения без

существенного ущерба динамическим свойствам, что делает

доступным приближенный анализ и синтез САР с ВД в процессе

поиска структур регуляторов.

При расчетах коэффициентов характеристического уравнения

для ВД с тактовой синхронизацией инвертора по положению ротора

приняты

,968,0



K ,37,1



K 577,0tg





При синхронизации по напряжению соответственно приняты

,907,0



866,0cos





Таблица 17.1

191

193

192

17.2. Устойчивость электропривода с вентильным

двигателем

17.2.1. Постановка задачи

Исследование динамики (в частности, асимптотической

устойчивости) вентильного электродвигателя на базе синхронного

двигателя и полупроводникового преобразователя с зависимым

инвертором тока выполнено в ряде работ [20, 40, 41, 53], в которых

не учитывается влияние механической части электропривода. В

некоторых из перечисленных работ, учитывая, что переходные

электромагнитные процессы в синхронной машине при наличии

короткозамкнутых демпферных обмоток протекают весьма быстро

и не оказывают существенного влияния на изменение частоты

вращения вала двигателя, рассматривают электромагнитные

процессы в предположении постоянства частоты вращения

двигателя. В этом случае дифференциальные уравнения вен-

тильного двигателя становятся линейными и удается дать их

строгое аналитическое решение.

При таком подходе вне поля зрения остаются такие

существенные факторы, как влияние нелинейности характеристик

холостого хода, конечной жесткости валопровода и соединительной

муфты, влияние внешней нагрузки, в общем случае нелинейно

зависящей от скорости вращения двигателя, наконец, некоторые

диссипативные силы. Следовательно, можно считать, что задача

определения областей устойчивой работы вентильного

электродвигателя в электроприводе с учетом конечной жесткости

валопровода, нелинейности характеристики холостого хода и

различной по виду функции характеристики нагрузки на валу

двигателя в настоящее время однозначно не решена.

Как известно, имеется большое количество методов

исследования устойчивости систем. Некоторые из них являются

чисто алгебраическими, например критерий Гурвица, другие –

частотными, например Михайлова. В последнее время матричные

методы исследования применяются чаще в силу компактности

записи, а также использования алгоритмов линейной алгебры.

В силу вышеизложенного в данной главе решаются следующие

задачи:

1. Получение полной системы дифференциальных уравнений

вентильного двигателя постоянного тока в электроприводе с учетом

нелинейности характеристики холостого хода; конечной жесткости

валопровода и различной (функциональной) характеристики нагрузки

(с ,2,1,1,0







где



- показатель зависимости характеристики

механизма от скорости вала).

2. Получение системы нелинейных уравнений и определение

параметров стационарных движений разомкнутой системы

электропривода.

3. Получение системы уравнений возмущенного движения для

исследования устойчивости стационарных движений

электромеханической системы с вентильным двигателем по

первому методу Ляпунова.

4. Получение в матричной форме рабочей формулы для

определения областей устойчивости стационарных движений.

5. Исследование устойчивости определенных невозмущенных

движений системы электропривода с вентильным двигателем.

17.2.2. Исходная система дифференциальных уравнений

Система дифференциальных уравнений вентильного

электродвигателя с учетом инерционности канала управления

задающего угла



, конечной жесткости валопровода, нелинейности

характеристики холостого хода и различной характеристики нагрузки

и допущений, принятых в [20], может быть представлена в виде

P, кВт

Гн

2,0 200 7,2 0,052 0,026

4000 6000 439 0,0056 0,0056

r, Ом

, с

J, кг

L Гн ,

R Ом

0,402 0,064 0,139 2 0,12 0,2

0,042 0,13 69,5 1 0,031 0,02

Приложение 17.1

195

194

   

 

       

 

 

 

   

 

 

     

 

   

 

   

 

   

 

  

 





































































































































































































































































;

;coscossin

2sin

;

sincos

;

cossin

;cossin

cos

sin2cos

cos

;sincos

cos

sin

cossin

cos

sin

;

cossin

002

ппп

ппк

пдэп

пк

ппк

пдэп

пк

MMMc

iLiFiiLiiL

iLLc

idF

LiFiriLiLL

UiRRU

iLL

iriLiLL

UiRRU

iLL

idF

LirU

adfkdadkqaq

aqad

kqkq

kqaq

aqaq

kdkd

kdad

adadad

adfkdaddad

qaqqaq

kqaqqaq

daddad

adf

adadfff



(17.8)

где

 

























LLR

sin31

- эквивалентное сопротив-

ление, учитывающее коммутацию тока в инверторе;

с - приведенная жесткость валопровода и соединительной

муфты;

, MM

- относительные моменты нагрузки и холостого хода

механизма;









, - угловая скорость вала и ее приращение;



- показатель характеристики механизма,





,2,1,0,1









;

 

0

























- нелинейная функция аппроксимации;













nfn

aiaiaiai 



















...

- аппроксимирующий

характеристику холостого хода двигателя полином.

Все остальные переменные в (17.8) являются общепринятыми

в предыдущих главах.

В системе уравнений (17.8) переменными состояния являются

приведенные относительные значения: тока возбуждения

синхронной машины



, осевых токов демпферных обмоток

(



); угла установки датчика положения (



) либо иногоо

пространственного угла между векторами напряжения и тока якоря

(



) или ЭДС и напряжения якоря (



); скорости вращения валала

двигателя (



); угла упругой деформации вала (





) и егоо

производной (







В дальнейшем для удобства записи введем следующие

обозначения переменных состояния:

;

1 f





;

п2



;





x ;

4 kd





;

5 kq





;





x ;







x 



В этом случае система уравнений (17.8) с учетом обозначений





iFR











перепишется в виде

   

;

cossin







































xxL

xLxrU

adadf

adadff

197

196

       

 

 

 

   

;sincos

cos

sin

cossin

cos

sin

3256362к

2дэп

32к

3к

xxrxxLxxxLL

UxRRU

xxLL

xLL

aqqaq

adad

daddad



















































   

 

 

       

;cossin

cos

sincos

cos

6132362к46

2дэд

32к

3к

xLxFxxrxxxLLxxL

UxRRU

xxLL

xLL

addadad

daqdad













































   

 

;

cossin

xxL

kqkdadad

adad























   

 

;sincos

xxL

kqkqaqaqaq



















 

       



; coscossin

2sin

321324325

xxLxFxxxLxxxL

xxLLcx

adadaq

aqad

















(17.9)

где

 

   

 

























































....

;

sin31

11101

axaxaxax

xxF

xLLR

Заметим, что уравнения (17.8) или система уравнений (17.9)

полностью определяют движение исследуемой электро-

механической системы электропривода.

В соответствии с общепринятым правилом в практике

исследования динамики систем (см. 17.2) в дальнейшем необходимо

определить установившиеся движения и составить уравнения

малых колебаний в окрестности найденных движений.

Установившиеся движения определяют так называемые

невозмущенные движения, а уравнения малых колебаний –

возмущенные движения.

17.2.3. Уравнения невозмущенного движения

В качестве невозмущенных движений, определяющих

установившиеся движения, выберем случаи, когда

.8,...,2,1 const,



ixx

(17.10)

Непосредственной подстановкой искомого невозмущенного

движения, определяемого (17.10), получим систему нелинейных

трансцендентных уравнений для определения параметров

. При

этом учитываем, что

. 0





Получим:

   

 

 

   

 

 

     

 



   

     



  

 

















































,0 ;0

;coscos

sin2sin

;0 ;0;

cossin

2coscos0

;sincos

2cossin0

;

8008060070

302010302040

30205030

50406010

3020306020к4060

20дэп

30205060306020к

20Љэп

xMxxMMcx

xxLxFxxxL

xxxLxxLLcx

xrxrxLxF

xxrxxxLLxxL

UxRRUK

xxrxxLxxxLL

UxRRUK

xrU

adad

aqaqad

kqkdad

dadad

acx

aqqaq

acx

(17.11)

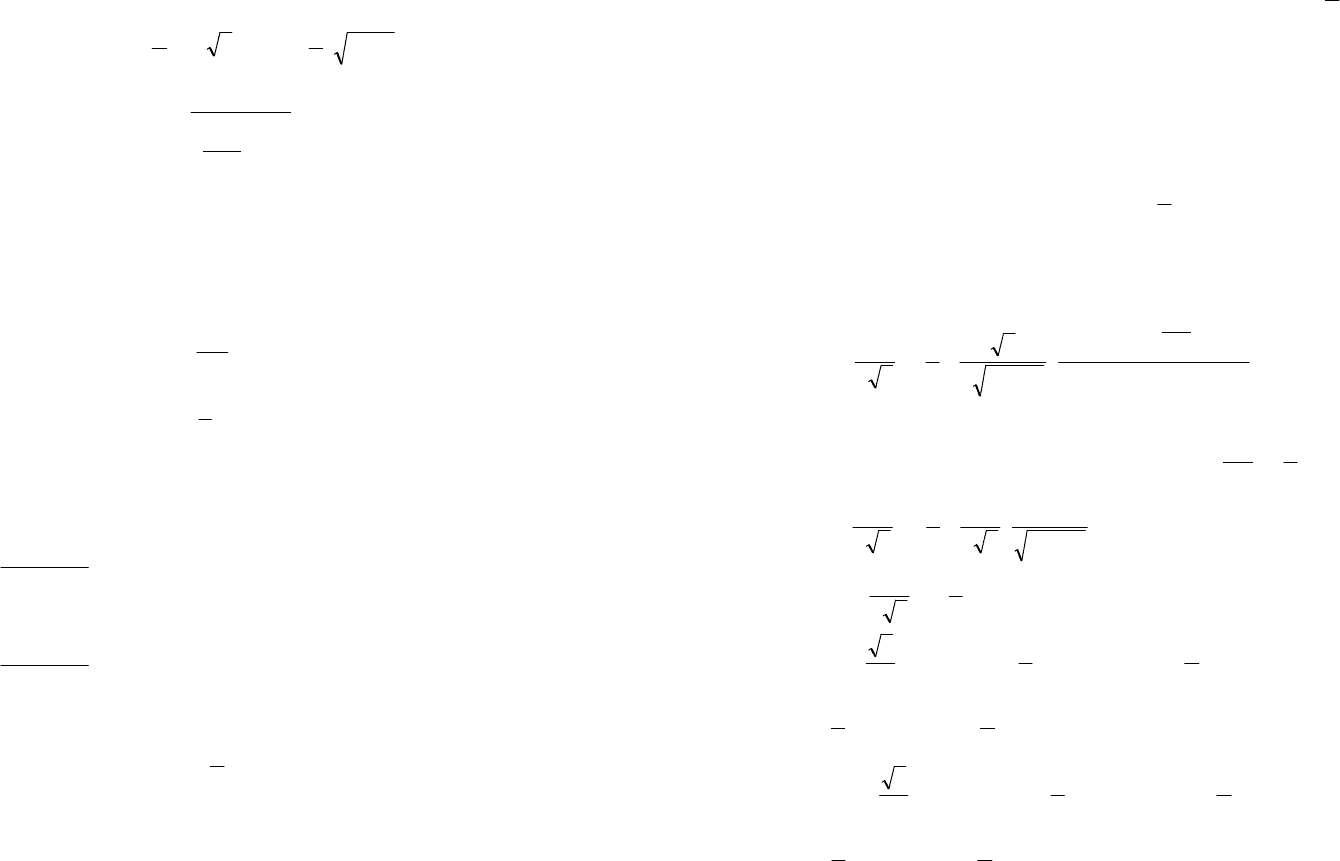
199

198

где

 



























































....

;

sin31

10110010

axaxaxax

xLLR

Анализ системы (17.11) позволяет определить некоторые

а именно:

 

 





















;0 ;0 ;0 ;

060070

80504010

MxMM

xxx

(17.12)

Для определения

с учетом (17.12) имеем

систему нелинейных трансцендентных уравнений

 

 

 

 

   

 

   



































.cos

2sin

;cossin

cos

;sincos

cos

sin

302010

6000

60103020306020

к20дэп

3020306020

к20Љэп

xxLxF

xxLLxMMM

xLxFxxrxxx

LLUxRRU

xxrxxx

LLUxRRU

aqadc

dada

qaqa

(17.13)

Для однозначного решения систем (17.12) и (17.13) необходимо

задавать следующие параметры электропривода (см. прил. 17.4)





cos











sin













, с,

Задачу определения установившихся режимов можно несколько

расширить, если ввести дополнительные выражения для определения

угла нагрузки



и угла коммутации вентилей инвертора



[20]:

















;

130

bbb

(17.14)

где

   

 

   











































































































































































33sin

sin

22sin

cos

;

33cos

cos

22sin

sin

;

sin

;cossin

cos

;

sincoscossinsin

sin

sincos

sin

1110

3003001

130130

xfxf

xLxL

(17.15)

201

200

Таким образом, по уравнениям (17.13), (17.14) с учетом

обозначений по (17.15) можно определить

;





Далее по выражению (17.12) определяется значение

. Для

этого необходимо задать значения параметров электропривода,

приведенные в приложении, за исключением





Полученная методика является наиболее общей из известных

и позволяет найти множество установившихся режимов типа

const



(см. расчетные характеристики рис.17.4).

17.2.4. Уравнения возмущенного движения

Для получения уравнений возмущенного движения в выражения

(17.9) подставим

xxx



, (17.16)

где

- малые отклонения (возмущения) от соответствующих

установившихся значений

const



Учитывая

const



, получим









;

cos

sin

32030230110

xLx

xxxLxxLxrxrU

adadf

adadfff















































       



   



   

 

   

;

sinsin

cos

sincos

cos

sin

~~~

cos

sin

cos

2303020

330206505605060

23060630203306020306020

к202дэ20дэ

330

20к230к

xxrxxr

xxxrxxLxxLxxL

xxxxxxxxxxxxx

LLxRxRRUxRR

xLx

Lxx

xLLxxLL

aqaqaq

dada

adad

daddad































































 

   

 

   

       

   

     

;

~~~

cos

sincos

cos

sin

cossin

cos

sin

cos

160

6106010230

330203020640460

406023060к63020

к3306020к306020

к202дэ20дэп

5330

20к230к

xxL

xLxFxLxFxxr

xxxrxxrxxLxxL

xxLxxxLLxxx

LLxxxxLLxxx

LLxRxRRUxRRU

xLxx

xLLxxLL

adadad

adad

addad

daddad

dada

qaqqaq



































































   

 

;

cos

sin

4404

33020230

xrxrxLL

LxxxLxxL

kdkdkdad

adadad













































;

cos

550

533020230

xrxr

xLLxxxLxxL

kqkq

kdadaqaq















 

   

     

       

 

;

cos

sin

cos

sin

2sin

cos

sin

2sin

13020

3321023010

30201043020

5302023020

330

77061











































xxxL

xxxLxFxxLxF

xxLxFxxxL

xxxLxxxLL

xxxLLxxxLL

xxLLxccxxJ

adad

aqaqad

aqadaqad

aqad

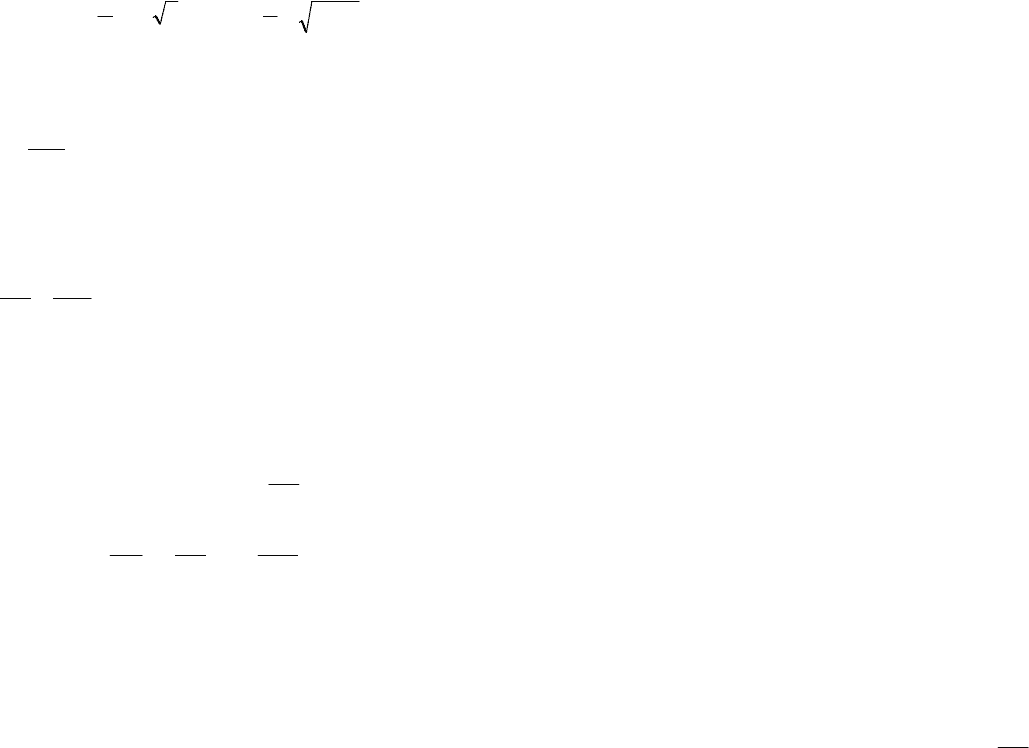
203

202























   



;

8807086

8060

080600770682

xxxMxxxx

MMxxMMxxcxxJ













(17.17)

Во втором и третьем уравнениях системы (17.17) приведенное

сопротивление принимает значение

 

sin31

xLLR



































В системе уравнений (17.17) учтена нелинейная

аппроксимирующая функция

       



 



nnn

axxa

xxaxxaxxa











1101

1102

11011100

...

~~~

и ее производная

    



  



, ...

1102

1101

1100













axxna

xxnaxxna

которые согласно формуле бинома Ньютона могут быть

представлены в виде

   





























































;

1011

xFxF

(17.18)

Заметим здесь же, что





33030330

cossin

sin xxxxx











33030330

sincos

cos xxxxx







Члены системы (17.17), содержащие

в первой степени,

определяют возмущенное движение, а все остальные члены -

невозмущенное движение (установившийся режим), и в уравнениях

указанной системы они составляют тождества.

В силу вышеизложенного и опуская для простоты записи волни-

стые черточки над переменными

, получим уравнение

возмущенного движения в матричной форме:





, (17.19)

где матрицы B и F имеют вид

;

0000000

000000

0000000

00000

0000

00000

0000

7876

555352

44434241

353332

24232221

14131211















bbb

bbbb

bbb

bbbb

0000000

00000

0000000

000

0000

0000000

787776

676564636261

3634333231

26252322















fff

ffffff

fffff

ffff

В векторном уравнении (17.19)





xxx

811

...,,,X

- матрица-

столбец размерности



Коэффициенты

матрицы B в (17.19) определяются нижесле-

дующими соотношениями:

;



















LLb

adf





;sin

3012

xLb









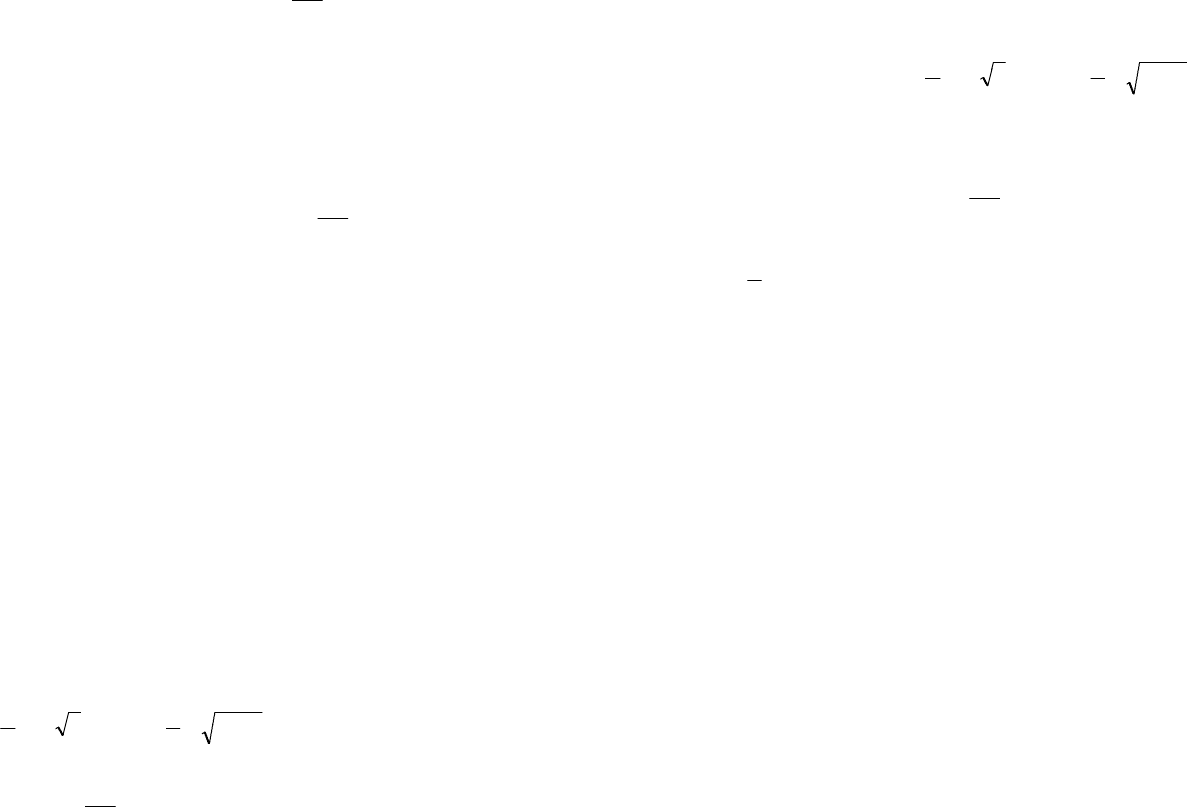
205

204





;cos

302013

xxLb









;

14 ad





;

































; sincoscos

30к

1д22

xLLKLb

dadcx











;cos

3020к23

xxLLb

dad 







;

24 ad





















; coscoscos

30к

1д32

xLLKLb

qaqcx















;sin

3020к33

xxLLb

qaq











;

35 aq



;





















;cos

302042

xxLb











;

44 kdad

LLb











;cos

3052

xLb













;sin

302053

xxLb







;

55 kqaq

LLb







;

166



;

276



;

278



Элементами матрицы

по (17.19) будут

;

11 f

















 

;cos

sincossin

3060к

30дэ

122

xxLL

xrRRKf

qaq





















;cossin

3020306020к23

xxrxxxLLf

qaq



















;

6025

xLf

















 

;

sin31

cossincos

13020к26

cxqaq

LLx

KxxLLf









































;

































 

;cos

sincoscos

3060кдэ

132

xxLLRRKf

dadcx





















;coscos

3020306020к33

xxrxxxLLf

dad



















;

6034

xLf





   

     

;sin

sin31

coscos

103020к

136

addad

qdcx

LxFxxLL

LLxKf











































;

44 kd







;

55 kq







 

;cos

3020

xxL



















 

     

;cos2sin

30103020

xLxFxxLLf

adaqad



















   

;sin

cossin

302010

xxLxF

xxLLxxLLf

aqadaqad









;cos

302064

xxLf







;sin

302065

xxLf



;













;

8060076



 xxMMf

;











;

8060078



 xxMMf



f .1



Уравнения возмущенного движения в виде (17.19) неудобны

для проведения исследований устойчивости невозмущенного

движения (17.10). В практике исследований обычно систему (17.19)

приводят к форме Коши. Процедура приведения уравнения (17.19)

к форме Коши формально решается следующим образом.

Умножим слева уравнение (17.19) на обратную матрицу

1

11 





Очевидно,



1

, где Е - единичная матрица размерности



. Тогда





, (17.20)

где

1



В результате преобразований система (17.19) приводится к

форме Коши (17.20).