Аракелян А.К., Афанасьев А.А. Вентильные электрические машины в системах регулируемых электроприводов. Том 2

Подождите немного. Документ загружается.

207

206

17.2.4.1. Матричный критерий устойчивости

Известно, что если в (17.19) и (17.20) все





8...,,2,1 0Re







то нулевое решение системы (17.20) асимптотически устойчиво

по Ляпунову. Таким образом, для исследования асимптотической

устойчивости автономной системы возникает задача определения

знаков корней характеристического уравнения

0 AE . (17.21)

Для этого можно использовать стандартные программы ЭЦВМ

для вычисления собственных чисел матрицы. Однако для

установления факта асимптотической устойчивости достаточно

выяснить знак



. Для этого, как известно [113], существуютт

методы установления принадлежности собственных чисел матриц

к левой полуплоскости без вычисления их значений.

17.2.4.2. Принцип построения матричных критериев

устойчивости

Пусть на плоскости комплексной переменной



задана

некоторая область

[285]. Обозначим

- совокупность всехех

матриц порядка n, все собственные значения которых

располагаются внутри области

;



- совокупность всех матриц

порядка n, все собственные значения которых лежат внутри

единичного круга с центром в начале координат на плоскости

комплексной переменной



. Предположим, что существует

оператор

, устанавливающий взаимнооднозначное соответствие

двух множеств:



. Тогда, если



, то оператор ор A от

матрицы A есть такая матрица порядка n, что









BAH

, и

наоборот, если В есть матрица из семейства



, то





ABH 

1

Здесь через

1

обозначен оператор, обратный оператору Н. Для

того чтобы матрица В принадлежала области



, необходимо и

достаточно, чтобы выполнялось условие

lim





Покажем это на примере диагональной матрицы.

Действительно, если В чисто диагональная матрица, то по главной

диагонали расположены ее собственные числа



...,, ,

. Отсюда

следует, что условие

lim





возможно в том и только в томм

случае, когда

0

для всех ni ...,,2,1



, ибо

есть чистоо

диагональная матрица, на главной диагонали которой

располагаются числа



...,, ,

. Отсюда следует следующее

утверждение: для того чтобы матрица А принадлежала области

, необходимо и достаточно, чтобы выполнялось условие









lim





Изложенный принцип далее используется для разработки

алгоритмов устойчивости линейных систем большой размерности,

в частности систем электроприводов с вентильным двигателем.

17.2.4.3. Построение критерия устойчивости

Рассмотрим систему дифференциальных уравнений

АX





, (17.22)

где А - матрица коэффициентов системы, непрерывно зависящих

от параметров автоматической системы (коэффициенты усиления,

постоянные времени, жесткости, моменты инерции и т.д.);

- вектор-столбец координат..

Чтобы система (17.22) была асимптотически устойчива,

необходимо и достаточно, чтобы все собственные значения



исходной матрицы А лежали в левой полуплоскости комплексной

переменной



, т.е. необходимо и достаточно, чтобы выполнялось

условие

0Re





для всех



1, 2, ...,

, где решения

алгебраического уравнения

0 EA . (17.23)

Построим матрицу В, используя известное дробно-линейное

преобразование, широко применяемое в теории аналитических

функций:







. (17.24)

Оно обладает тем свойством, что мнимая ось,

рассматриваемая как окружность бесконечного радиуса,

209

208

переводится им в окружность единичного радиуса с центром в

начале координат. Если комплексная переменная



движется вдоль

мнимой оси, то комплексная переменная



перемещается вдоль

единичной окружности. Так как каждой точке левой полуплоскости

комплексной переменной



соответствует вполне определенная

точка, принадлежащая кругу единичного радиуса, и наоборот, то

это соответствие однозначно









Подставим значение



из выражения (17.24) в (17.23). Тогда

уравнение (17.23) примет вид







 EA

. (17.25)

Умножая (17.25) на (





1

) и имея в виду, что

aAAa



получим:









011  AA

или





0 EAEA .

Умножим это уравнение на (-1),









0 EAEA .

Полученное выражение умножаем на





1

 EA

слева





















EAEAEAEA

окончательно имеем













EEAEA

. (17.26)

Обозначая в уравнении (17.26) матрицу









MEAEA 

1

получим 0 EM .

Матрицу М преобразуем следующим образом:

















   

 

 

.22







EAEEEAEA

EEEAEAEAEAM

Легко увидеть, что если все собственные значения



исходной

ì àòðèöû êî ýô ô èöèåí òî â

А лежат в левой полуплоскости

комплексной переменной



, то все собственные значения



преобразованной матрицы коэффициентов М находятся внутри

круга единичного радиуса, и наоборот, если хотя бы одно



окажется в правой полуплоскости, среди



найдется такое, для

которого









Известно, что собственные значения матрицы М являются



, ...,



, то собственными значениями матрицы

являются



, ...,



. Тогда, если система (17.22) устойчива,а,

последовательное возведение матрицы М в степень уменьшает

абсолютную величину собственных значений



, ибо все



лежатт

внутри единичного круга с центром в начале координат и по модулю

меньше единицы. Возведение матрицы в степень рекомендуется

выполнять так, чтобы каждая последующая матрица являлась

квадратом предыдущей, т.е. по закону

;

kk 22

, ... .

В этом случае в оперативном запоминающем устройстве

ЭЦВМ не надо постоянно удерживать матрицу М, так как каждый

раз используются лишь полученные у нее степени.

17.2.4.4. Оценка устойчивости по следу матрицы М

Возможность оценки устойчивости по следу матрицы









вытекает из того факта, что след

S M



устойчивой системы

стремится к нулю при





. Рассмотрим этот вопрос подробнее.

Известно, что след матрицы

представляет собой сумму всех

собственных значений



, взятых в той же степени, что и матри-

ца

kkkk

S 



...

321

Вопрос о стремлении матрицы

к нулю при





можетет

быть решен в общем случае путем изучения следов

последовательных степеней, взятых в таком количестве, какой

ï î ðÿäî ê ì àòðèöû

n. Однако в некоторых случаях при исследовании

211

210

реальных автоматических систем матрицу М можно не возводить

в степень. Эти случаи выделяет теорема Зубова из его лекций по

теории управления.

Если при исследовании системы (17.22) выполняется

í åðàâåí ñòâî

nS 



, то среди







, (



1, 2, 3, ..., n) найдется

хотя бы одно, для которого удовлетворяется условие









Доказательство. Это утверждение легко доказывается от

противного: Допустим, напротив, что все









. Тогда

 







. (17.27)

Но по условию справедливо неравенство

 























. (17.28)

Тогда из неравенства

 

 

 















1 1

, а также из неравенстваа

(17.27) следует, что



















1

. (17.29)

Из противоречия неравенств (17.28) и (17.29) непосредственно

следует истинность сформулированного утверждения. Таким

образом, если модуль суммы диагональных элементов М

превышает порядок матрицы n, то среди







всегда найдется

такое, для которого









Из рассмотренного неравенства









вытекает, чтоо

достаточно построить матрицу М, и если ее след по модулю

превышает порядок матрицы n, то исследуемая точка пространства

допустимых значений параметров не принадлежит области

асимптотической устойчивости. Однако если соотношение









не удовлетворяется, никаких выводов относительно

неустойчивости сделать нельзя. В этом случае следует

рассмотреть следы последовательных степеней матрицы М:

















. ..., ; ;

42 k

SSSS MMMM



Для оценки устойчивости достаточно опираться на изучение

следов трех последовательных степеней. Если начиная с некоторого

следы трех последовательных степеней матрицы

убывают,т,

исследуемая система рассматривается как устойчивая.

Äëÿ âû÷èñëåí èÿ ýëåì åí òî â ì àòðèö

В и F исследуемой системы

необходимо для невозмущенного движения задавать динамические

параметры, приведенные в прил. 17.3.

Исследования стационарных режимов и устойчивости

движения системы в целом выполнены на ЭЦВМ по блок-схеме,

приведенной на рис.17.3. в прил. 17.3. Расчетные характеристики

даны на рис.17.7. Анализ этих данных позволяет сделать

следующие выводы:

1. Система уравнений (17.9) с учетом обозначений















является наиболее полной системой дифференциальных

уравнений исследуемого электропривода с вентильным двигателем,

позволяющей учитывать влияние конечной жесткости вала привода,

различного характера нагрузки, а также нелинейность

характеристик холостого хода. При необходимости угол нагрузки



и угол коммутации вентилей инвертора



могут быть

определены равенствами (17.14).

2. Множество возможных стационарных движений может быть

определено равенствами (17.12)-(17.15).

3. Приведенная методика исследования устойчивости стацио-

нарных движений на основе матричного критерия В.И. Зубова по-

зволяет построить области допустимых изменений параметров

управления САР, что является важным моментом задач анализа и

синтеза систем с ВД.

Приложение 17.2

Исходные переменные и параметры системы электропривода

Двигатель серии СТД 4000 2РУ;

4000



кВт;

4580



кВА;А;

9,0cos





(опережающий);

6000



В;

439



А;

102



В;

283



А; КПД = 97,5 ; маховой момент ротора -

мкг 278 GD

; максимальный вращающий момент при к. з. (при

213

212

пуске)

макс



номМ. Частота вращения

3000



об/мин;

критическая частота вращения

2230

рк



об/мин;

1012 С

Нм.

Расчетные параметры, о.е.

;655,1



;

3 ;465,0 ;0014,0 ;03,0















cxfHff

KirU

;851,1 ;851,1 ;129,0 ;722,1 ;722,1



 dqaqad

LLLLL

;01,0 ;602,3 ;00899,0 ;14286,0 ;14286,0

дд









RLrLL

 

;1011 ;10 ;

sin

;1,0 ;0,1











 JCMM

;0 ;0004,0 ;2,1,0,1











kqkdkqkda

rrLLU

Коэффициент приведения роторного тока

.4,1

рп







adW

KKmW

Характеристика холостого хода двигателя

о.е.,

0 0,367 0,581 0,742 0,916 1,115

1,24

о.е.,

0 0,165 0,252 0,33 0,417 0,563

0,709

о.е.,

1,364 1,427 1,497 1,554 1,618

о.е.,

0,913 1,049 1,233 1,417 1,68

Функция аппроксимации характеристики





.00164,072189,121016,3

24140,158769,155178,73532,1

1010





xxxxxF

Приложение 17.3

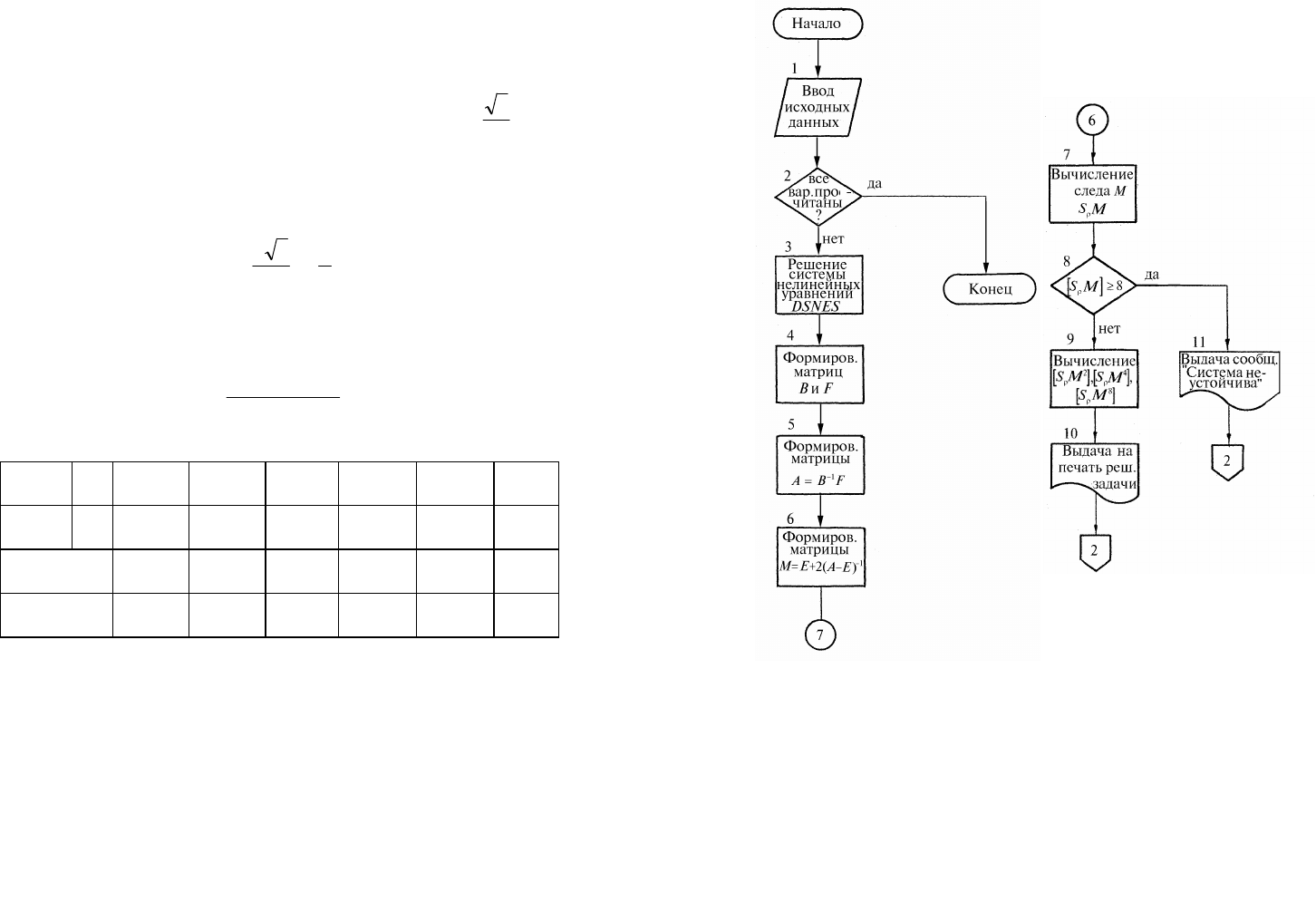
Описание блок-схемы решения задачи

Блок 1. Ввод исходных данных с ПК.

Блок 2. Проверка. Если все заданные варианты просчитаны,

то передача управления на завершение работы программы.

В противном случае переход к блоку 3.

Блок 3. Для выбранного варианта решение системы

нелинейных алгебраических и трансцендентных уравнений методом

Рис. 17.3. Блок-схема решения задачи

212

215

214

Стеффенсена (стандартная программа DSNES) для определения

параметров невозмущенного движения



Блок 4. Формирование матриц В и F.

Блок 5. Вычисление матрицы А.

Блок 6. Вычисление матрицы М.

Блок 7. Вычисление следа матрицы









Блок 8. Проверка. Если









, то переход к блоку 11.

В противном случае - к блоку 9.

Блок 9. Вычисление













842

, , MMM



SSS

Блок 10. Выдача на печать результатов решения программы.

Переход к блоку 2.

Блок 11. Выдача на печать сообщения "Система неустойчива".

Переход к блоку 2.

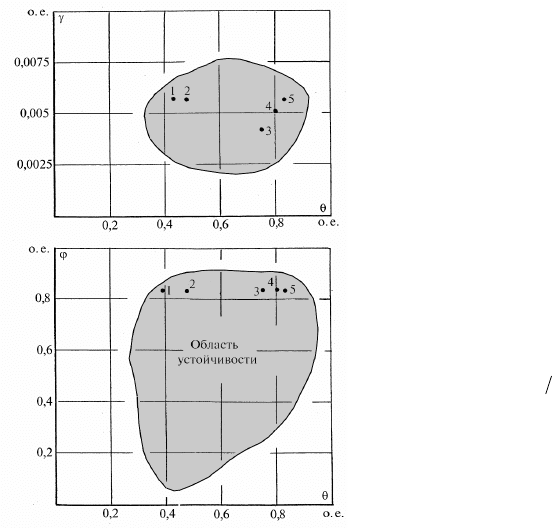
Рис. 17.4. Расчетные

области устойчивых

движений разомкнутой

системы электропривода

насосного агрегата при

вариации внешней нагрузки:

;6 ;8265,0

U

;к

* 



;

MМ 



;





;

-1

k





1 -

;5,0



2 -

;6,0



3 - ;85,0



4 -

;95,0



5 - 0,1



17.3. Электромеханическая связь в системе

электропривода с вентильным двигателем

Ниже анализируются явления упругих колебательных

процессов, демпфирование в многомассовой электромеханической

системе (МЭМС) и влияние на эти процессы электромеханической

связи ВД [14, 28]. Вентильный двигатель на основе типового

синхронного двигателя имеет значительную, по сравнению с

эквивалентным ДПТ, постоянную времени якорной цепи, в общем

случае ослабляющую электромеханическую связь в САР и

ухудшающую демпфирующую способность ВД.

Некомпенсированная составляющая продольной реакции якоря

способствует возбуждению автоколебательных электро-

механических процессов и может служить источником

параметрического резонанса. Переменная составляющая

электромагнитного момента ВД от высокочастотных составляющих

тока якоря и напряжения этой обмотки может возбуждать

вынужденные колебания на низких частотах вращения

электропривода и при определенном сочетании электромеханических

параметров привести к резонансным явлениям. Зависимость

предельной логарифмической амплитудно-частотной характеристики

ВД от значения и способа задания пространственных углов (







) между векторами ЭДС и тока якоря, напряжения и тока,

напряжения и ЭДС якорной обмотки ВД, соответственно может быть

причиной ограничения пределов статической и динамической

устойчивости СД и ИТ и снижения электромеханической связи по

аналогии с коммутационными ограничениями в САР с ДПТ [35, 206].

Затронутая проблема усложняется для мощных (несколько

МВт и более) и быстроходных (3000 об/мин и более)

многомассовых электромеханических систем с виброактивным

вентильным двигателем. В упругом механическом звене подобных

систем могут возбуждаться несколько главных крутильных

колебаний различной формы отдельных вращающихся масс.

Предварительно по расчетной схеме (рис.17.5, а, прил. 17.4) можно

оценить характер колебаний в МЭМС и степень влияния этих

колебаний на скорость, ток (электромагнитный момент) ВД и на

упругий момент в механическом звене.

217

216

Главные собственные частоты недемпфированных колебаний

МЭМС находим на основе уравнения Лагранжа, без учета действия

внешних моментов и диссипативных сил по [35]:







, (17.30)

где

- постоянные коэффициенты, определяемые моментами инер-

ций сосредоточенных вращающихся масс и жесткостями упругих

звеньев;

1

 p

- обобщенные угловые координаты вращающихся

масс;

- оператор дифференцирования; )1(1



i ... 4.

Абсолютные значения корней

, характеристическогоо

уравнения (17.30) определяют собственные частоты

недемпфированных колебаний



. По частотам рассчитываются

амплитуды колебаний

отдельных масс и формы этих колебаний

[14] (см. прил. 16.4, табл. 17.2, рис.17.6,б)

По данным табл.17.2, первое главное двухузловое колебание в

валопроводе может возбуждаться приблизительно при

шестикратной угловой скорости электропривода. Это много выше

верхнего предела регулирования скорости САР и потому из

дальнейшего рассмотрения исключается. II-III формы колебаний

происходят в интервале регулирования скорости электропривода,

причем II - в окрестностях номинальной скорости ВД, а III - в

окрестностях скорости, при которой частота переменной

составляющей электромагнитного момента ВД может совпадать

Расчеты



- из-за громоздкости опущены, см. [159].

с частотой вращения вала механизма. Эпюры амплитуд главных

êî ëåáàí èé (ðèñ.17.5,

б) указывают на возможность упрощения

расчетной схемы (рис.17.5,а) и сведения ее к двухмассовой

(ДЭМС). Колебания ТГ-СД и СМ-РМ происходят попарно на часто-

те II формы синфазно и с амплитудами

2212



;

4232



Главные

колебания и

Собств.

частоты,

Относительная амплитуда колебаний,

их формы



ТГ(ВВ) СД СМ РМ

I — двухузловое 5,74 a

=6,54 a

=1,0 a

= - 2,8 a

=5,175

II — двухузловое 0,89 a

=1,32 a

=1,0 a

= -0,85 a

=2,6

III — одноузловое 0,154 a

=1,007 a

=1,0 a

= - 0,65 a

= - 3,45

Системное 0,80 a

=1,25 a

=1,0 a

= - 0,73 a

=1,8

Таблица 17.2

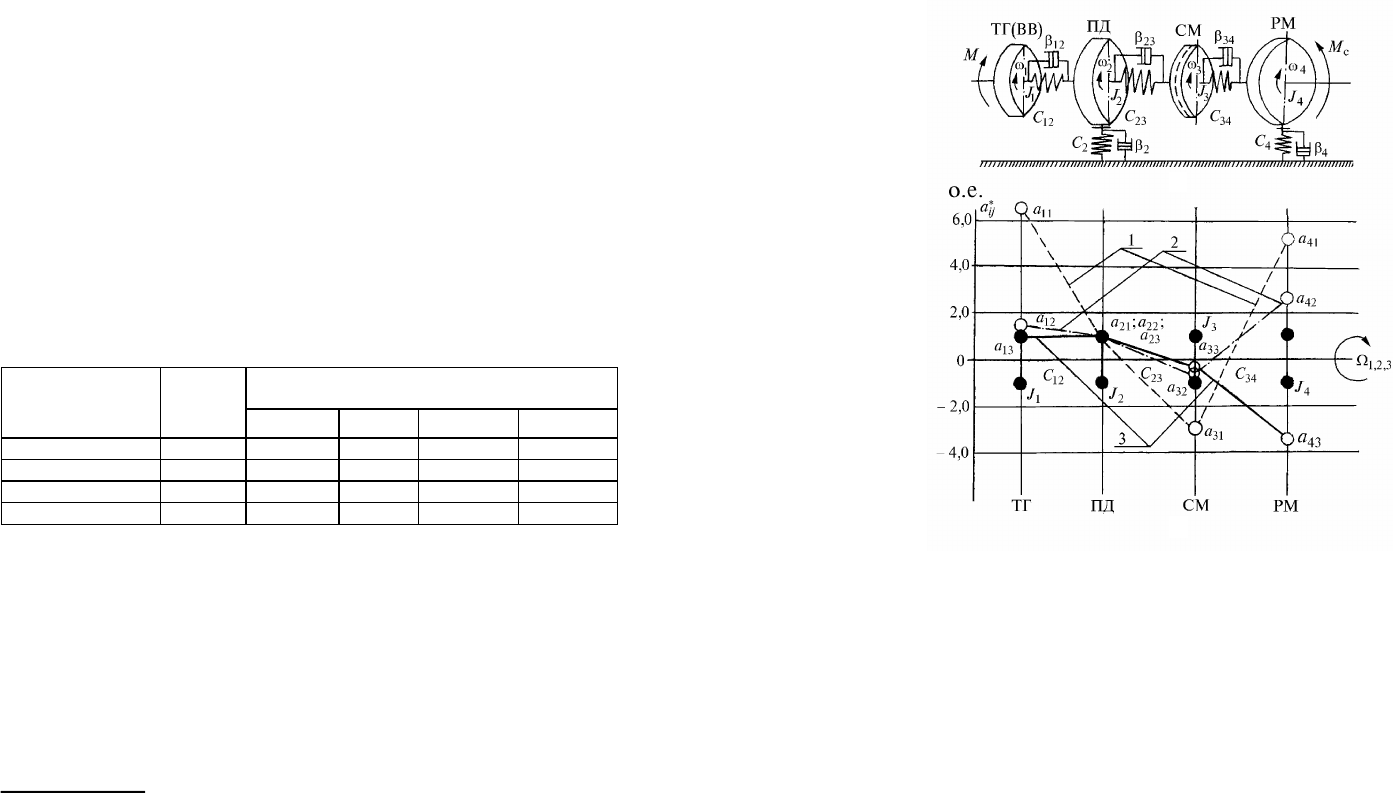
Рис. 17.5. Расчетная схема: а) - многомассовой упругой

электромеханической системы и б) - эпюры главных колебаний: ТГ (ВВ) -

тахогенератор (или вращающийся возбудитель); ПД - приводной

электродвигатель; СМ - соединительная муфта; РМ - рабочая машина;

4321

,,, JJJJ

- моменты инерции вращающихся роторов;



- жесткость

и коэффициент вязкого трения элементов валопривода; М, М

электромагнитный момент и момент сопротивления механизма;

4321

,,, 

- мгновенные угловые скорости роторов;

321

,, 

- угловые

частоты главных крутильных колебаний валопривода;

- амплитуды

крутильных колебаний соответствующих роторов; 1 - эпюра первого

двухузлового главного колебания; 2 - то же второго (двухузлового) и 3 -

третьего (одноузлового) колебаний

219

218

а на частоте III - формы

2313



;

4333



, что равносильно

защемлению четвертой вращающейся массы.

Следовательно, расчетную ДЭМС можно представить

эквивалентными массами

1

2

, связанными упругим

элементом

экв12

Для соблюдения условия допустимости пренебрежения связи

между упругими механическими процессами в валоприводе и

электромеханическими (электромагнитными) ВД используем

значения коэффициента электромеханической связи (

эc

) ДЭМС

с ВД.

Операторные изображения электромагнитного момента ВД

М(р) и упругого механического момента М

(р) могут быть

определены из системы (17.30). Аппроксимируя входные и

выходные величины ИТ непрерывными функциями и эквивалентируя

ВД по якорной цепи уравнением электрического равновесия, по

(11.42) запишем систему (17.30) в явном виде для нулевых условий

с заданным

const





[14].

















     

   

























;

2м

21экв1212

•н.з2

2212

1112

1н.з1п

пэквэквпп

ppKpM

CpM

pipWpM

ppJpMpM

pppWpE

pipTRpEpU

(17.31)

Линейное приближение системы (17.31)

получим исходя из

допущений. Пренебрегая насыщением СД, коммутационными

процессами инвертора и составляющей ЭДС якорной цепи ВД от

гармонических токов высоких порядков, трансформаторных связей

роторных контуров, получим





11еонз1

cos







pKpW

Электромагнитный момент ВД представим гладкой

составляющей, следовательно:









1пмонз2

cos





piKpW

Переменную составляющую М(р) учтем лишь при

исследовании уравнения электромеханической связи в окрестностях

резонансных частот III формы главных колебаний. Влияние

переменной составляющей М(р) (пульсирующей с частотой, равной

шестикратной частоте вращения вала ВД) на II форму главных

колебаний будет пренебрежимо мало.

Входное напряжение инвертора тока

представим (из-за вве-

денной непрерывной отрицательной обратной связи по току)

функцией входного тока





, а момент сопротивления механизмаа





- линейной функцией координаты



. Получим изображения

искомых моментов:

 























;

apapapapapa

cpcpcpc

apapapapapa

bpbpbpb

(17.32)

где

- постоянные коэффициенты характеристическогоого

уравнения системы (17.31) и полиномов числителей соответ-

ствующих изображений (прил.17.4).

Предположив, что быстродействие полупроводникового

преобразователя ДЭМС с ВД не ограничено его СИФУ или

Расчеты



- из-за громоздкости опущены, см. [159].

218

221

220

естественным запаздыванием (т.е.



от



, т.е.





вхп



UKpU

, находим, что постоянные коэффициенты

характеристического уравнения (17.32), а также определитель

Гурвица, составленный из этих коэффициентов, и все его

диагональные миноры положительны при любых соотноше-

ниях

1

2

Следовательно, вентильный двигатель при управлении с

const





в разомкнутой ДЭМС обладает определенным запасом

устойчивости благодаря некоторой демпфирующей способности,

равносильной введению диссипативных сил в упругом звене, однако

исключенных в (17.30) и (17.31).

Для количественной оценки степени электромеханической связи

САР с ВД проанализируем соответствующие АФЧХ передаточных

функций ДЭМС по возмущающему воздействию:

 





 





 













Исключение из рассмотрения передаточных функций по управ-

ляющему воздействию (



) обусловлено малым влиянием

этих возмущений на электромеханическую связь по сравнению с

возмущением, действующим непосредственно на вал двигателя

(рис.17.5,б).

Модули искомых амплитудно-частотных характеристик

получены из















при

от







 

   





 

 

;

///1

10эквэкв2экв2

экв

10эквэкв2

эквэкв2

10эквэкв2



































мм

TJJJJJTT

JJJJJJTTJJ

JJJ

(17.33)

 

 





 

 

 

 

15.12 по15.12 по

2222

эквэкв2









ММ

TTJJJ

(17.34)

Результаты расчетов амплитудно-частотных характеристик по

(17.33), (17.34) и соответствующих коэффициентов затухания ()

для двух главных частот демпфированных колебаний

pII



pIII



приведены в табл. 17.3 и на рис.17.6,б. Исходные данные для

расчетов приведены в прил. 17.5.

При возмущающем воздействии и

экв



АЧХ ДЭМС с ВДД

имеют явно выраженные резонансные максимумы, находящиеся в

окрестностях II и III форм главных недемпфированных колебаний

с частотами соответственно



III

61 

(



собственная частота колебания вала СД). При этом влияние

электромагнитной инерции якорной цепи ВД существенно

проявляется в II форме колебаний и относительно большем

2

, а

в III форме - при

2

малом. Это указывает на относительно слабое

поглощение электрическими контурами якоря и ротора ВД энергии

механических колебаний масс в ДЭМС в противоположность

синхронному двигателю, включенному по нормальной схеме.

Результат подтверждает вывод о слабом влиянии демпферных

обмоток на частотные характеристики ВД [41].

Полагая в (17.33) и (17.34)

экв



, вычислим эффект

подавления резонансов в окрестностях зоны

pIII



и ослабление

его в окрестностях

pII



. Это указывает на хорошую

1,0

экв

I

41,0

экв

I

Резо-

нансные

частоты



Элект-

ромагн.

пост. якоря

экв

 

jA

 

jA

 

jA

 

jA



 *



0,0 - - - - 6,7

6,9

—2

25,2

1,83

—2

II — 0,8

16,25 - - - - 29,5

0,157

—2

100

0,415

—2

0,0 0,99

7,31

—2

0,935

—2

76,3

—2

1,035

7,0

—2

0,635

11,4

—2

III—

1,33

16,25 2,3

3,16

—2

2,46

—2

34,6

—2

1,21

6,0

—2

0,735

9,9

—2

Таблица 17.3

Примечание.



1*

;

c1314



;

TT 

эвк

экв

;





212

экв



 IIII

221

223

222

демпфирующую способность ВД с малой эквивалентной

индуктивностью якорной цепи, одновременно способствует и

лучшему использованию электрической машины.

Относительно слабое демпфирование механических колебаний

в САР с ВД при

экв

T

вызвано, как и в ДПТ, ослабляющим

действием индуктивности якорной цепи на электромеханическую

связь ВД. Для количественной оценки уровня этой связи по аналогии

с (17.33) и (17.34) получим комплексный коэффициент

эс

САР с

ВД, модуль которого для

pII

(1 

;

pIII

61 

)

выразится согласно (17.33) и (17.34) соотношением

 





 

 

 

 

01эквпм

экв

01эквмп

экв01отм

12экв

1экв

01п

экв

эс











TTTIII

TTTIkTIII

IITI

(17.35)

Это выражение позволяет найти при безынерционном преобразо-

вателе (



) для разомкнутой САР (

от



) коэффициент элек-

тромеханической связи, который в зависимости от параметров

звеньев САР, в частности от





,,,

дэкв qd

LLLT

;





моэквэкв

,, KRIT

;





21экв

, III

, может принять значения





эс

0 K

Расчетные значения

эс

при вариации части указанных выше

параметров приведены на рис.17.7,а. Пределы измерения

0,305,0

эс



за исключением





отэc



, говорят о том, чтоо

САР на основе мощных типовых синхронных двигателей серии СТД,

в зависимости от сочетания параметров механической части,

может обладать, согласно [144], свойствами слабой и

существенной электромеханической связи. Следовательно, при

исследовании динамических процессов подобных систем при пуске

или при внешних возмущениях необходимо учитывать вероятность

слабой связи, исключающей взаимодействие электрической и

механической частей САР как единой электромеханической

системы. В исследуемой системе свойства существенной

электромеханической связи явно выражены в окрестностях низшей

резонансной частоты, это указывает на значительные колебания

тока якоря ВД и на повышенный уровень поглощения энергии

механических колебаний непосредственно СД либо отвод ее в

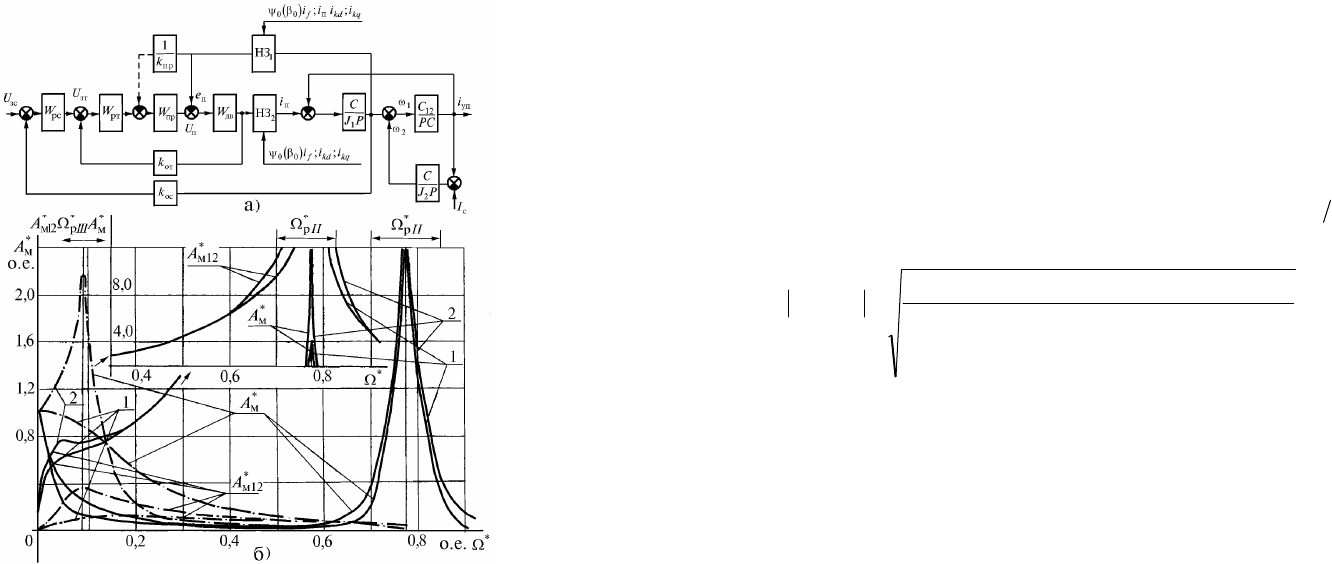
Рис.17.6. Структурная схема а - САР с ВД, амплитудно-частотные

характеристики электромагнитного момента





jA

и б - упругого

момента







при возмущающем воздействии рабочей машины:

зтзс

,UU

- сигналы задания скорости и тока двигателя соответственно;

двпрртрс

,,, WWWW

- передаточные функции регуляторов (скорости и тока),

преобразователя частоты и электродвигателя соответственно;

отос

, KK

- коэффициенты обратных связей;

нз,нз

- нелинейные звенья;

суп

,ii

- токи якоря двигателя, определяемые упругим моментом

и моментом статистического сопротивления;

пр

- коэффициент усиления

преобразователя частоты по напряжению;



- несущая угловая скорость

вращения валопривода;

pII



pIII



- резонансные угловые частоты,

обусловленные второй и третьей формами главных крутильных

колебаний. 1 - АЧХ при 0,0

экв

T ; 2 -АЧХ при

25,16

экв

T

––––––––

41,0

экв

J

; - · - · - · -

1,0

экв

J

225

224

питающую сеть. Следовательно, в данном конкретном случае

пренебрегать демпфированием электропривода упругих механи-

ческих колебаний, тем более на низших резонансных частотах,

неправомерно. Эти обстоятельства учтены при оптимизации САР

по скорости и по току.

Рассмотрим влияние токоограничения на электро-

механическую связь ВД в замкнутой САР с жесткой отрицательной

обратной связью по току в режиме пуска. Расчетные кривые





эквотэc

,TKK

(рис.17.7,б,в) показывают, что при высокомм

быстродействии преобразователя с ИТ отрицательная обратная

связь обратная по току в значительной степени уменьшает

электромеханическую связь ВД. Следовательно, по аналогии с САР

с приведенным (одномассовым) жестким механическим звеном с

ДПТ быстродействующие схемы токоограничения могут быть

использованы в САР ДЭМС с ВД с синхронными двигателями

большей мощности (серии СТД и др.) для формирования пусковых

и регулировочных характеристик.

Уровень электромеханической связи ВД в САР,

оптимизированной по критерию быстродействия методами

подчиненного регулирования с последовательной коррекцией,

оценим с помощью того же коэффициента электромеханической

связи. Установим значение

эc

САР при оптимизированном контуре

тока. С учетом внутренней связи по ЭДС вращения ВД для САР

(рис.17.6, а) можно записать следующее уравнение [32]:

   





 

piRpTpK

pWpiK

пэквэкв1эc

ртпот





, (17.36)

где













поттэквтрт





 pKKTaRpTapW

- передаточная функция

регулятора тока;

ртт





 TTa

- коэффициент, характеризующий степень демп-

фирования колебаний тока якоря;

рт

- постоянная интегрирования контура тока.

После преобразования (17.36) представим в конической

форме [144]:















pbpaM

, (17.37)

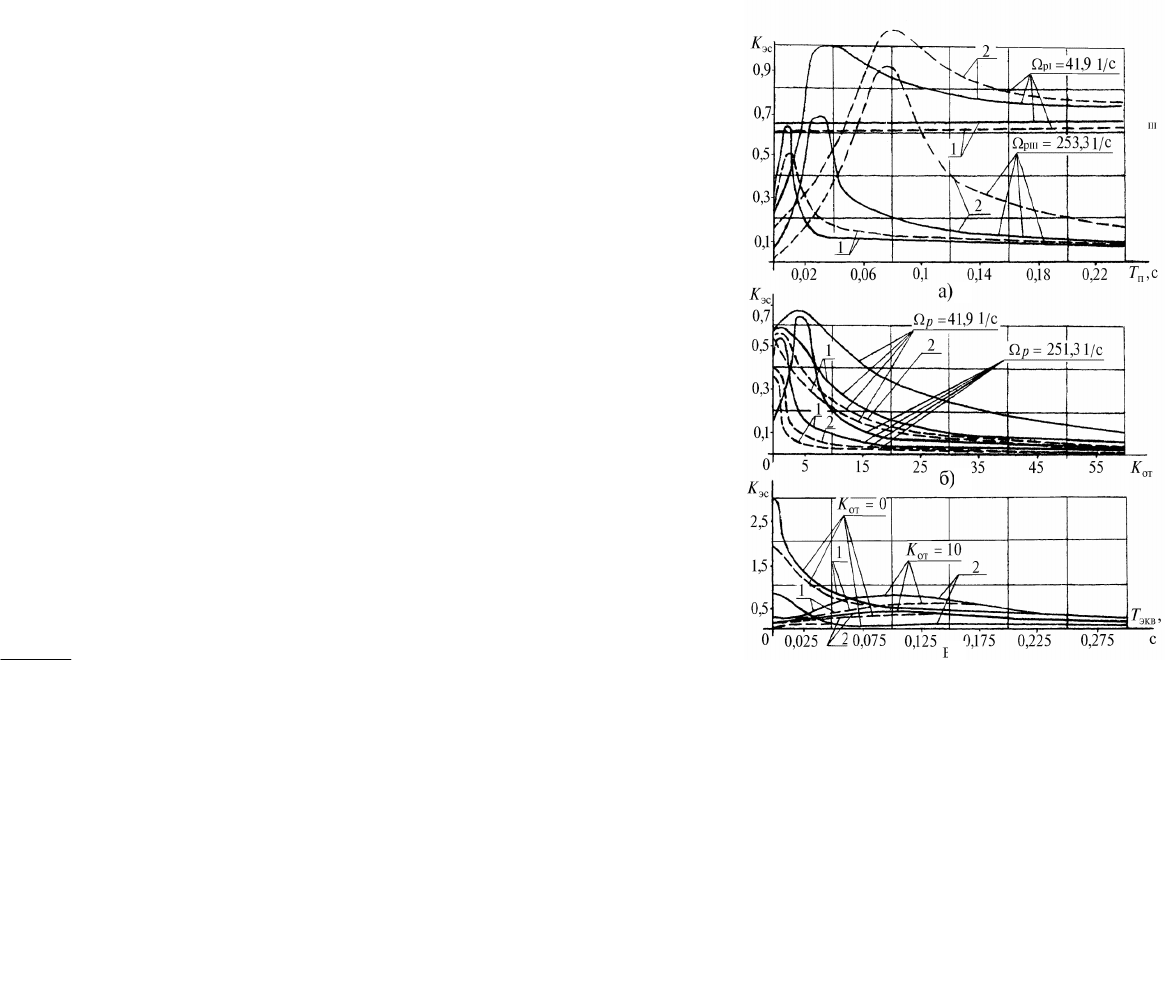
Рис.17.7. Коэффициент электромеханической связи K

эс

оптимизированной по быстродействию системе: а – при регулировании

тока якоря в функции постоянной времени преобразователя

; б – то

же в функции коэффициента отрицательной обратной связи по току

якоря K

от

; в – то же в функции эквивалентной постоянной времени

якорной цепи Т

экв

рI



;

рIII



– резонансные частоты соответствующих

форм главных демпфированных колебаний; по а: 1 – K

от

= 0 ; 2 – K

от

= 10 –

для K

эс

(

); по б: 1 –

= 0,036 с: 2–

= 0,1 с — для K

эс

от

); по в: K

эс

(

экв

);

––––

;1,0

экв

I

- - -

;41,0

экв

I

225