Аракелян А.К., Афанасьев А.А. Вентильные электрические машины в системах регулируемых электроприводов. Том 1

Подождите немного. Документ загружается.

214 215

Из системы уравнений (4.126), (4.127) можно определить

коэффициенты

 

























































.cossincossin

,sincossincos

,cossincossin

,sincossincos

nnnn

nnn

nnnn

nnn

iyixriyixr

iyixriyix

(4.128)

По этим формулам определяют две системы коэффициентов

А и В.

Первая система коэффициентов (их обозначают

















BABA











,,,

) находится на базе четных узловых точек





mn ,,3,2,1,2 







, являющихся образами четных точек

(4.124).

Вторая система коэффициентов (их обозначают

















BABA





,,,

) находится на базе нечетных узловых

точек





12,,5,3,1,





mkkn 

, являющихся образами нечетных

точек (4.125).

Далее, используя первую систему коэффициентов, можно по

формулам (4.126), (4.127) найти образы нечетных точек





12,,5,3,1,





mkkn 

, которые, вообще говоря, не будут лежать

на границах заданной области в плоскости z, поэтому их называют

внеконтурными нечетными узловыми точками. Например, из

первого уравнения (4.126) получим

   

.sincos

sincos

iBiA

iBiAx

























(4.129)

После подстановки в (4.129) и в три других аналогичных

выражения для



kkk

yxy

зависимостей (4.128) с

),,3,2,1(,2 mn 







получим формулы для координатт

внеконтурных нечетных узловых точек, которые зависят только от

координат четных узловых точек. Например,





 

































т.д.и,,,,

,,,,,

22222

yxyxyy

yxyxxx

(4.130)

Сами эти функции приведены в [220].

Радиус

внутренней окружности кольца можно найти по

формуле

.,,3,2,1,

sincos

2222

























(4.131)

Аналогично изложенному можно, используя вторую систему

коэффициентов ,BиA найти образы внеконтурных четных

узловых точек через координаты нечетных узловых точек





 





















т.д.и,,,,

,,,,,

222

kkkk

kkkkk

yxyxyy

yxyxxx

(4.132)

Вид этих функций также приведен в [220].

Для радиуса справедливо

.12,,5,3,1,

sincos



















kkkk



(4.133)

Итерационный процесс, позволяющий определить с заданной

степенью точности координаты узловых точек, целесообразно

начинать при m=4. Стартовое (нулевое) приближение четных

узловых точек можно найти с помощью графических построений

[220].

216 217

Схема итерационного процесса выглядит следующим образом

1.Определяется радиус

внутренней окружности кольца по

формуле (4.131), исходя из стартового приближения четных

узловых точек.

2.При помощи формул вида (4.130) по четным узловым точ-

кам

2



2

находятся внеконтурные нечетные узловые точки



3.Внеконтурные нечетные узловые точки



сносятся на

контур заданной области и определяются нечетные узловые точки



4.Определяется радиус

внутренней окружности кольца по

формуле (4.133) по найденным



5.При помощи формул вида (4.132) по нечетным узловым

точкам



находятся внеконтурные четные узловые точки

2



2

6.Внеконтурные четные узловые точки

2



2

сносятся на

контур заданной области и определяются более точные четные

узловые точки

2



2

, т.е. получаются исходные данные для

пункта 1.

Итерационный процесс считается законченным тогда, когда все

внеконтурные точки (четные и нечетные) будут отклоняться от

заданного контура на величину меньшую допустимой ошибки



Если при выбранном m этого не удается достичь, то число узловых

точек удваивается, что проще всего сделать, приняв четные и

нечетные узловые точки при исходном m только за четные, т.е. число

четных узловых точек становится равным 2m.

Определив координаты узловых точек с заданной степенью

точности по формулам (4.128), вычисляем коэффициенты A и B,

относящиеся к первой и второй системам (они построены на базе

соответственно четных и нечетных точек). Необходимо, чтобы

обе эти системы коэффициентов совпали между собой, по крайней

мере, с точностью до величины допустимой ошибки



После окончания итерационного процесса более точное

значение радиуса

внутренней окружности кольца можно

определить по формуле

sincos











nnnn

(4.134)

где

.2,,3,2,1 mn 



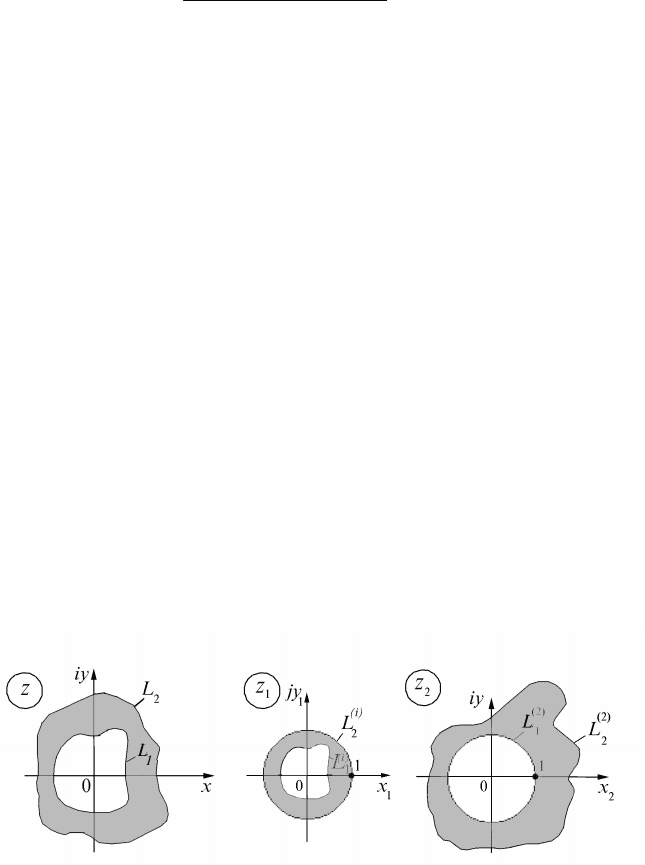
Конформное отображение двухсвязных областей на основе

последовательного отображения односвязных областей

Конформное отображение кругового кольца на двухсвязную

область, ограниченную контурами

, причем контур

находится внутри

, можно свести к последовательным

конформным отображениям внешности или внутренности

единичного круга на односвязную область, границей которой

является соответственно контуры

заданной двухсвязной

области.

Итерационный процесс решения этой задачи имеет следующую

схему.

1. Внутренность единичного круга в комплексной плоскости

с помощью функции





zfz



конформно отображается на

внутренность внешнего контура

исходной комплексной

плоскости z (рис. 4.24).

2. Внутренний контур

при помощи функции





zfz





кон-

формно отображается на контур





, находящийся внутри

единичного круга плоскости

Рис. 4.24. Последовательное отображение односвязных областей

218 219

3. С помощью функции





221

zfz 

внешность единичной

окружности в плоскости

конформно отображается на внешность

контура





плоскости

4. С помощью функции





zfz





внешний контур





плоскости

отображается на внешний контур





в плоскости

и далее процесс повторяется, начиная с пункта 1].

Алгоритмы конформных отображений внутренности и

внешности единичной окружности соответственно на внутренность

и внешность произвольного контура известны [143, 220].

Итерационный процесс продолжаем до тех пор, пока внешний и

внутренний контуры не будут совпадать (с заданной точностью)

соответственно с единичной окружностью и окружностью радиуса



, т.е. до тех пор, пока с заданной точностью не получим

круговое кольцо. Затем каждую из окружностей 1

z и





разбиваем на 2m равных частей и выбираем две системы точек:

четную





z ;

rz 





;









;

m,,3,2,1 





и нечетную

1

z ;





;





;

12,,5,3,1





mk 

Отобразив эти точки последовательно при помощи функций

















112211

,,,, zfzfzfzf

nnnnnn





получим соответственно

четные и нечетные узловые точки в плоскости z. По эти узловым

точкам при помощи формул (4.128) находим коэффициенты

и строим конформно отображающую функцию в виде

усеченного ряда Лорана (4.120).

В [220] доказано, что рассмотренный итерационный процесс

является сходящимся.

Конформное отображение кругового кольца

на двухсвязную область, ограниченную многоугольниками

с прямолинейными сторонами (аналог формулы

Кристоффеля-Шварца для двухсвязных областей)

Общее выражение для функции, конформно отображающей

круговое кольцо в плоскости t на двухсвязную область в плоскости

z, ограниченную прямолинейными многоугольниками, впервые

было получено Н.И. Ахиезером в 1928 г. [67].

Г.М. Голузиным доказана теорема [133, 149], согласно которой

двухсвязная область, ограниченная кривыми Жордана (т.е. кривыми

без самопересечений), всегда может взаимно - однозначно

(однолистно) отображаться на круговое кольцо, если заданной точке

на границе области соответствует заданная точка на границе кольца.

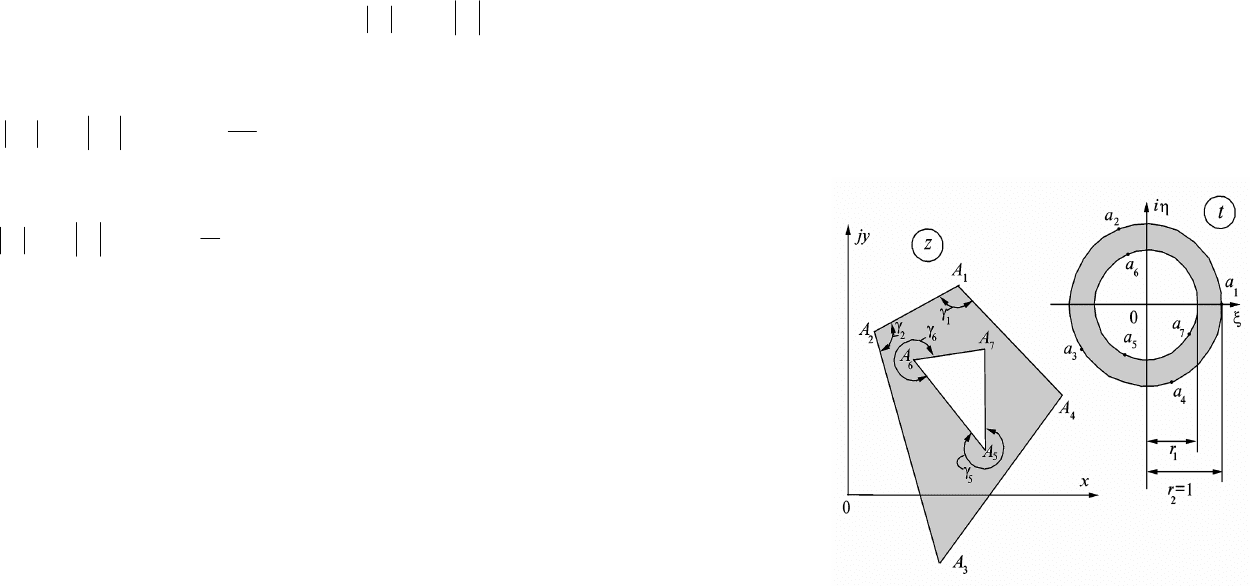
Обозначим через





mkA

,,2,1 



вершины прямолинейных

многоугольников плоскости z, причем

RSm





, где S, R - число

вершин соответственно внешнего и внутреннего многоугольников

(рис. 4.25). Этим вершинам будут соответствовать их образы - точки





mka

,,2,1 



в плоскости t.

Рис. 4.25. Конформное отображение кругового кольца на двухсвязную

область с прямолинейными границами

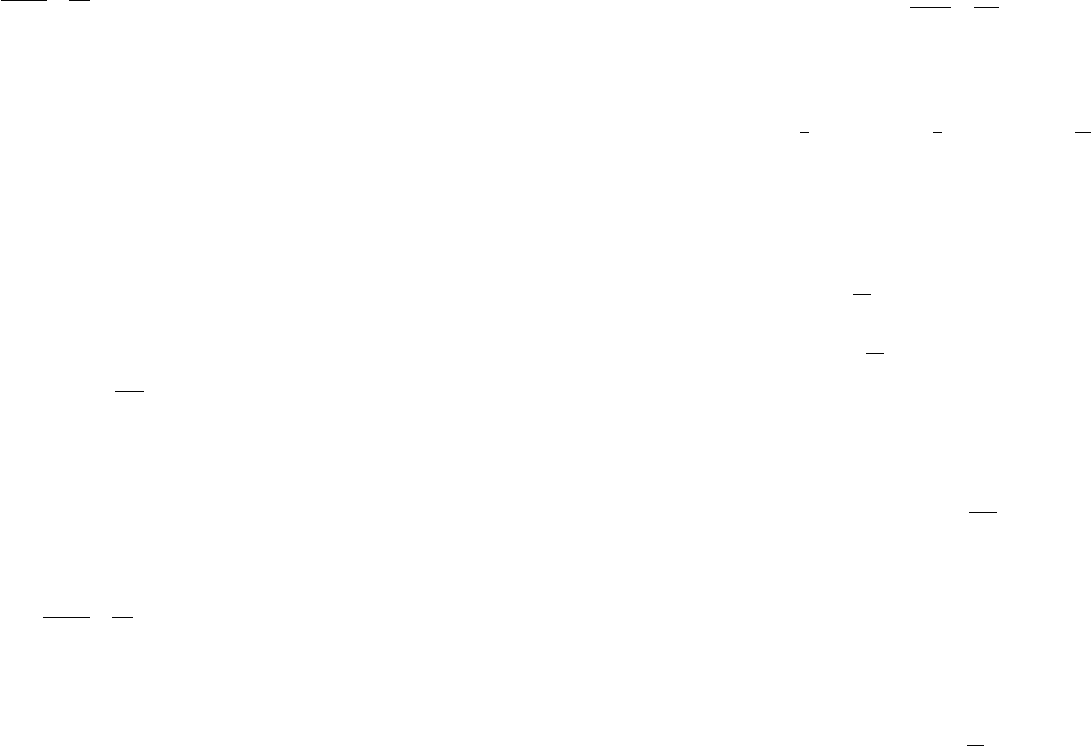
220 221



- внутренний угол при вершине

Отображающая функция





находится из дифференциальногоо

уравнения, являющегося аналогом известной формулы

Кристоффеля-Шварца [162, 174].









ПП













rat

tdz

, (4.135)

где









; постоянные





mkaC

,,2,1, 



и радиус

подлежат определению.

Значение одной из постоянных

можно задать произвольно,

расположив ее на соответствующей окружности кольца. Остальные

постоянные подлежат определению численными способами,

аналогичным способам, применяемым при отыскании постоянных

в дифференциальном уравнении Кристоффеля-Шварца, которое

задает конформное отображение верхней полуплоскости на

внутренность многоугольной односвязной области.

Уравнению (4.135) можно придать более компактный вид, если

ввести новую переменную



согласно выражению

,lnt

j 





(4.136)

в котором



- некоторая вещественная постоянная, выбираемая

произвольно.

Из (4.136) следует









. (4.137)

После подстановки (4.137) в (4.135) можем получить





 









tdz

, (4.138)

где

















; (4.139)

 





rrrH

4/1

101

2cos21Пsin2 





– (4.140)

– первая тета-функция Якоби (общее число этих функций - четыре);





1П 





. (4.141)

Переменную



в (4.138) можно выразить, учитывая (4.136) и

(4.139), через t

.ln

j



(4.142)

Тета-функция Якоби (4.140) может быть представлена также

в виде бесконечного ряда

        

.5cos23cos2cos2

 rrr

(4.143)

Уравнение (4.136) устанавливает связь комплексной плоскости

t с новой комплексной плоскостью



. Образом точки





ert

будет

точка в плоскости VjU







с координатами

 

























.ln

,2,1,0,2

kkU 

(4.144)

Легко увидеть, что образом кругового кольца (рис.4.7) в

плоскости t будет прямоугольник в плоскости



(рис.4.26).

Функция

 

,lnt







как видно из (4.144), многозначна. Обратная ей функция





однозначна. Поэтому вся плоскость



может быть покрытаа

бесконечным количеством прямоугольников, ширина которых

равна вещественному числу



2 , а высота - мнимому числу

.ln









(4.145)

222 223

Рис. 4.26. Образ кругового кольца в плоскости



Величины



2 и





являются периодами двоякопериоди-

ческой мероморфной

(эллиптической) функции [67, 162]

   





 

tdz

tzd

tgtG 

где





- функция, конформно отображающая круговое кольцо на

двухсвязную область с прямолинейными границами.

Функция (4.145) устанавливает связь между периодами





.ln









(4.146)

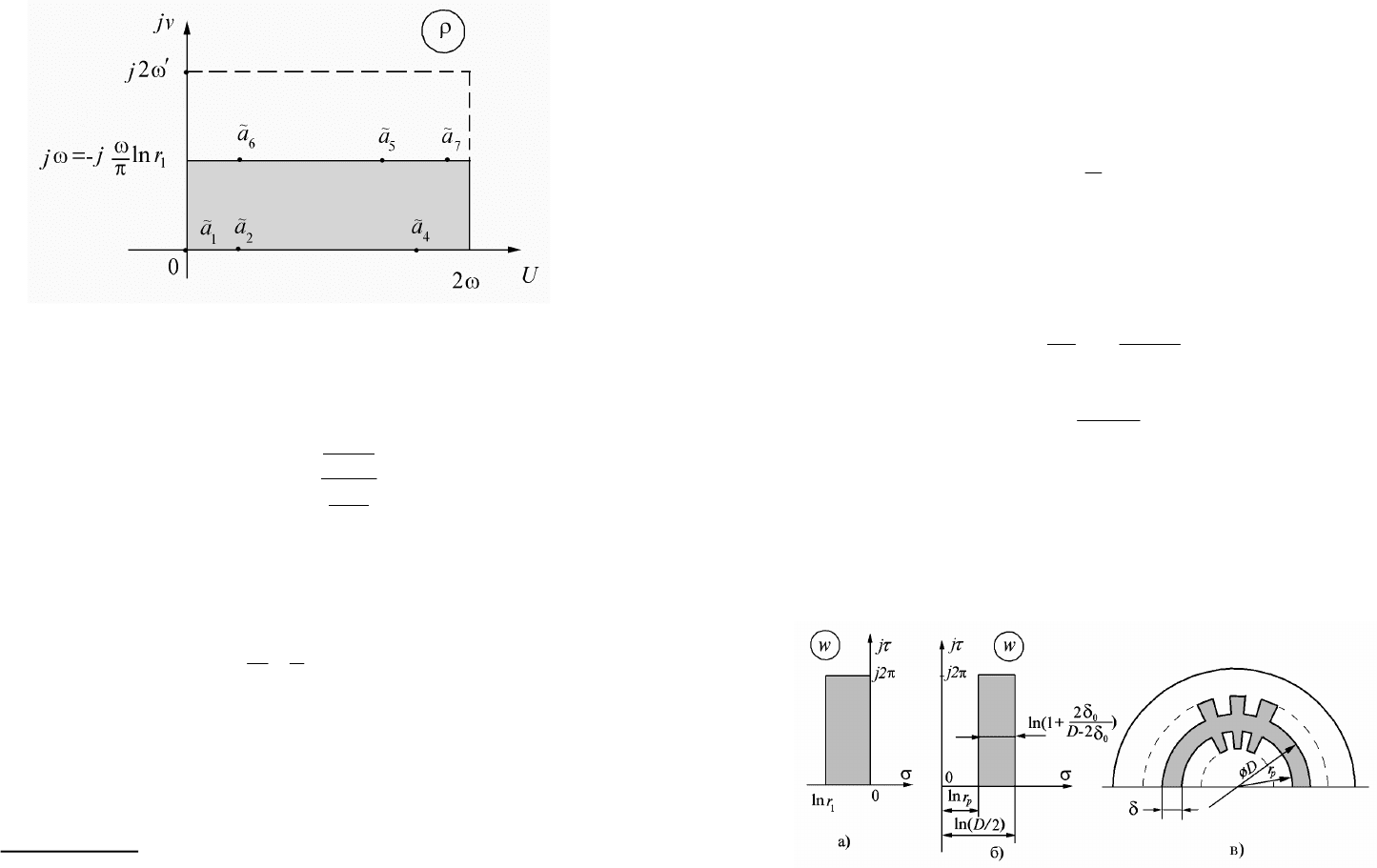
Круговое кольцо в плоскости t (рис. 4.25) можно преобразовать

в прямоугольник в плоскости

(рис. 4.27,а) с помощью уравнения

tjw ln











, (4.147)

где ,2,1,0,2,ln



















kkr .

Функция комплексного переменного называется мероморфной (дробной), если

она не имеет других особенностей, кроме полюсов. Двояко периодические

мероморфные функции называются эллиптическими.

Кольцевому зазору в плоскости







будет соответство-о-

вать его образ в плоскости

с размеромм

.ln







(4.148)

В плоскости размер зазора составит, как видно из рис. 4.26,

величину

ln r









. (4.149)

Учитывая размеры прямоугольников - образов кругового кольца

на рис. 4.26 и 4.27, а - можем записать выражения для магнитных

проводимостей зазора соответственно в комплексных плоскостях



и w

 

r















(4.150)

 









(4.151)

В электрических машинах воздушный зазор с двухсторонней

зубчатостью (рис.4.27,в), имеющий минимальный размер



приводят к "гладкому" кольцевому зазору размером



, используяя

коэффициент Картера





0 







(4.152)

Рис. 4.27. К расчету магнитной проводимости кольцевого

воздушного зазора

224 225

С помощью уравнения (4.116) условная "гладкая" кольцевая

область воздушного зазора между магнитными сердечниками

(рис. 4.27), в конформно преобразуется в прямоугольник плоскости

w (рис. 4.27,б) с размером зазора

1ln



















(4.153)

Магнитная проводимость этого прямоугольника будет равна

 

  

2/21ln









(4.154)

При конформных преобразованиях, как известно, магнитные

потенциалы, магнитные потоки, магнитные проводимости и

индуктивности являются инвариантными величинами [133].

Поэтому магнитные проводимости (4.151) и (4.154) должны быть

одинаковыми. Приравнивая их друг к другу, найдем

 

2/21











(4.155)

Это равенство совместно с (4.152) позволяет в первом

приближении определить радиус внутренней окружности кругового

кольца (рис. 4.25), являющегося образом двухсвязной области с

прямолинейными границами. Найденный стартовый размер

будет уточняться до требуемой точности в процессе вычисления

постоянных C и

с помощью дифференциальных уравнений

(4.135) или (4.138).

4.12. Параметры синхронной явнополюсной

электрической машины

Будем полагать, что функция





tfz



, конформно

отображающая круговое кольцо в плоскости

на двухсвязную

немагнитную область между статорным и роторным сердечниками

(рис. 4.23) в плоскости z, нам известна.

В полярной системе координат радиальные и тангенциальные

составляющие напряженности магнитного поля в точке





ert

плоскости t будут соответственно равны

   













(4.156)

где u - скалярный магнитный потенциал.

На границе двухсвязной области в плоскости z для нормальных

и касательных составляющих напряженности магнитного поля

будет справедливо

   









(4.157)

   

















(4.158)

где производные отображающей функции (4.120) находятся для гра-

ничных окружностей кольца по формулам

tCi











(4.159)

tCi













(4.160)

На основе походов, изложенных в предыдущих параграфах 4.1-

4.9, можем аналитически определить магнитное поле в круговом

кольце плоскости t.

Будем считать, что магнитное поле создается только трехфазной

обмоткой статора и в начале является продольным. Магнитный

поток основной гармоники по продольной оси (продольная ось

ротора совпадает с магнитной осью фазы A статора, т.е. угол между

этими осями





) через наружную границу двухсвязной области

в плоскости z в пределах одного полюса равен

         

   

 

,,,1/

0,0



















rlkB

lkBlB

mdN

(4.161)

226 227

где









mdNd

BBk /



- (4.162)

- коэффициент формы продольного поля якоря;





mdN

- амплитуда основной гармоники нормальной составляю-

щей магнитной индукции по продольной оси на наружной границе

двухсвязной области в плоскости z;





- нормальная составляющая магнитной индукции

продольного поля якоря в точке пересечения наружной границы

двухсвязной области положительной частью продольной оси;

)(

- нормальная составляющая магнитной индукции поля

якоря в точке наружной окружности кругового кольца (в среде2)

с координатой 0





при





;







- протяженность полюсного деления по наружной границе

двухсвязной области, включая и контуры пазов статора;

   





 ,,1,,1

; (4.163)

l - активная длина машины.

Аналогично при поперечном положении ротора











будем иметь

         

   

 

,0,0,1/

















rlkB

lkBlB

mqN

(4.164)

где









mqNq

BBk /



- (4.165)

- коэффициент формы поперечного поля якоря;

Вычисляя первые гармоники индукции продольного и

поперечного поля якоря, получим формулы для коэффициентов его

формы

 





 





  

.cos

2/0,

0,04















(4.166)

Эти коэффициенты будут зависеть только от геометрии

воздушного зазора и обмоточных данных якоря, если принять

магнитные проницаемости статорного и роторного сердечников

равными бесконечности. Тогда, согласно формуле (4.48),

распределение радиальной составляющей магнитной индукции на

наружной границе кругового кольца







будет

   













nFn

cos

(4.167)

или с учетом выражения (4.3) для





 

.cos















nkI

(4.168)

После подстановки (4.168) в формулу (4.166) для

коэффициентов формы поля получим

 

  

.cos

2/0,

cos

0,04





























nwn

(4.169)

Из (4.168) следует

 

2 nw















(4.170)

После подстановки этого выражения в формулы (4.161) и

(4.164) для магнитных потоков основной гармоники по продольной

и поперечной осям получим

 





 

qda

















(4.171)

где





. 0,0,1

















rdr

(4.172)

Эти потоки, вращающиеся синхронно с ротором, будут

наводить в обмотке якоря ЭДС самоиндукции, амплитудные

значения которых

228 229

 





 

1 mqd

qda

wqda

kwl

kwE











(4.173)

где

 

wdr

nwn















(4.174)

Формула (4.173) позволяет получить выражения для

индуктивных сопротивлений и индуктивностей реакции якоря по

продольной и поперечной осям

   





 

qdaqda

kwl









(4.175)

Теперь представим, что магнитное поле создается только

обмоткой возбуждения, расположенной на роторе по продольной

оси. Магнитный поток основной гармоники поля возбуждения

÷åðåç í àðóæí óþ ãðàí èöó äâóõñâÿçí î é î áëàñòè â ï ëî ñêî ñòè

z в

пределах полюсного деления





 будет

         

   

 

,0,1/

















rlkB

lkBlB

mfr

mfN

(4.176)

где









 





















BBk

mfr

mfN

mfNf

const,,1

cos

const,,14

(4.177)

- коэффициент формы поля возбуждения.

Как и в предыдущем случае примем магнитные проницаемости

статорного и роторного сердечников равными бесконечности. Тогда

из формулы (4.48), заменяя магнитный потенциал вихревых токов

ротора





на магнитный потенциал обмотки возбуждения

(умноженный на коэффициент 2/3), получим для радиальной

составляющей индукции поля возбуждения на наружной

окружности кругового кольца с учетом (4.10), (4.82)

 

,cos

sin4

cos































nFn

(4.178)

где

- суммарное число витков обмотки возбуждения (на всехх

полюсах).

После подстановки этого выражения в формулу для

коэффициента формы поля возбуждения (4.177) будем иметь





 

const,,1

cos

sin

const,,14

















































(4.179)

Магнитный поток основной гармоники поля возбуждения

(4.176) будет иметь с фазой обмотки статора максимальное

потокосцепление (ось этой фазы совпадает с продольной осью

ротора)

 





 

,Ф

1 f

wff

fwdaf

kwkw









(4.180)

где

 





sin8

















(4.181)

;1,2,3,1,-21,,1









kknrr





. const,0,1





rdr

(4.182)

230

Взаимная индуктивность обмотки возбуждения с фазой

обмотки статора (по потоку основной гармоники поля возбуждения)

будет, очевидно, изменяться при вращении ротора по

косинусоидальному закону. Амплитудное значение этой

индуктивности будет





 

kwkw

wff

daf











 (4.183)