Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

Solution of the problem 487

The potential χ is o f the form

χ(r) =

cosh µr +

sinh µr for all R

< r < R

and moreover satisﬁes χ(R

) = χ(R

) = V , which leads to the system of equations

A e

−µR

+ B e

µR

= R

V ,

A e

−µR

+ B e

µR

= R

V .

Solving this linear system, we obtain

χ(r) =

r sinh(µ∆R)



sinh µ(R

− r) + R

sinh µ(r − R

)



with ∆R = R

− R

. Then, differentiating, we get th e values of the electric ﬁeld on

the left and on the right of R

, and the difference is

E(R

) − E(R

−

) =

∂ϕ

∂ r



r=R

−

∂χ

∂ r



r=R

= µV



coth µR

+ coth µ∆R −

sinh µ∆R



Thus, for small µ, we have

σ =

V ǫ

+ R

The total charge is therefore

Q = 4πR

σ =

2π

V R

+ R

5. With the data in the text, since Q ¶ 10

−9

C, we obtain µ

−1

¾ 6 m, or, adding

correctly the proper factors }h and c,

µ ¶ 3. 10

−43

kg,

which is a very remarkable result. (Compare, for instance, with the elect ron mass

= 9.1 ·10

−31

kg.)

488 Differential forms

Sidebar 6 (Integra tion of differential forms) Let ω be a differential k-form.

In R

, it would be easy to give a meaning to the integral of ω on (a subset of) R

(see Deﬁnition 17.33, pa ge 471).

In order to deﬁne the integral of ω on a k-dimensional “surface” S (also called

a k-dimensional manifold), one starts by transforming S into a ma nifold ∆,

which is indeed a subset of R

, by means of a change of coordinates. Let f denote

the inverse change of coordinates, that is, the map from ∆ ⊂ R

into S :

f : ∆ −→ S ⊂ R

x 7−→ f ( x).

A point x ∈ R

in the space R

is mapped to f ( x). How are the tangent

vectors in R

transformed? Since tangent vectors correspond to “differences between

two p oints of R

,” the image by the change of coordinates of a vector v attached

to the point x will be v 7→ d f

. v, that is, the result of evaluating the differential

form d f

(given by the differential of f at the point x) at the vector v. It is often

customary to write f

∗

= d f the differential of f (without indicating precisely at

which point it is considered).

From the change of coordinates, a k-differential form on ∆, the “inverse image

of ω by f ,” which is denoted f

∗

ω, may be deﬁned by pu tting

( f

∗

ω) : (R

)

−→ R,

( v

, . . . , v

) 7−→ f

∗

ω( v

, . . . , v

)

def

= ω( f

∗

, . . . , f

∗

Using the deﬁnition of the integral of a dif ferential k-form on R

, it is then possible

to deﬁne:

def

∆

∗

ω.

Of c ourse, this deﬁnition can be shown to be independent of the choice of f .

∆

f ω

∗

Chapter

Groups

and group representations

18.1

Groups

DEFINITION 18.1 A group (G, ·) is a set G with a product law “·” deﬁned on

G ×G, such that

1. “·” is associative: (g · h) ·k = g ·(h ·k) for all g, h, k ∈ G;

2. (G, ·) has an identity element e, that is, an element of G such that

e · g = g · e = g for any g ∈ G;

3. any element in G is invertible, that is, for any g ∈ G, there exists an

element h ∈ G such that g · h = h · g = e. This element is unique; it is

denoted g

−1

and is called the inverse of g.

DEFINITION 18.2 A group (G, ·) is abelian or commutative if the product

law is commutative, that is, if g ·h = h · g for any g, h ∈ G. An abelian group

is often denoted additively: one writes g + h instead of g · h.

490 Groups and group representations

For commutative groups, the deﬁnition can thus be rephrased as follows:

DEFINITION 18.3 An additive group is a pair (G, +) such that

′

. “+” is an addition law on G, which is associative and commutative;

′

. (G, +) has an identity element 0

such that

∀g ∈ G 0

+ g = g + 0

= g;

′

. any G is invertible, that is, for any g ∈ G, there e xists an element

h ∈ G such that g + h = h + g = 0

. This element is d enoted −g and

is called the opposite of g.

Example 18.4 The set GL

(R) of invertible square matrices w ith real coefﬁcients of size n, with

the law given by the product of matrices, is a group; for n ¾ 2, it is non-abelian.

Example 18.5 The set of symmetries of a molecule, with the law given by composition of

maps, is a group.

Example 18.6 The set of rotations of t he vector space R

(rotations ﬁxing the origin) is a

commutative group.

Example 18.7 Consider t h e oriented space E = R

with its euclidean structure. Let G denote

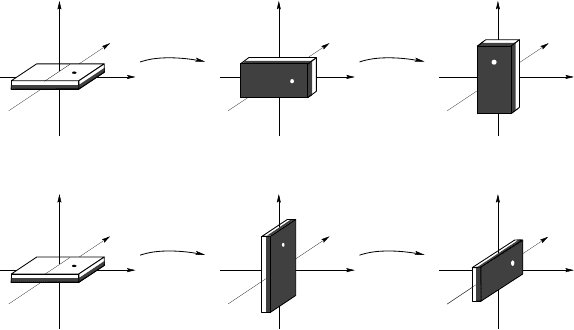
the set of rotations of E centered at the origin 0. Then (G, ◦) is a noncommutat ive group.

Indeed, if R

denotes the rotation with axis O x and angle π/2, and if R

denotes the rotation

with axis Oy and angle π/2, the following transformations of a domino show that R

◦ R

Linear representations of groups 491

18.2

Linear representations of gr oups

A group may be seen as an a bstract set of “objects,” together with a table

giving the result of the product for every pair of elements (a “multiplication

table”). From this point of view, two groups (G, ·) and (G

′

, ⋆) may well have

the same abstract multiplication table: this means there exists a bijective map

ϕ : G → G

′

which preserves the product laws, that is, such that for any g

, g

in G, the image by ϕ of the product g

·g

∈ G is the product of the respective

images of each a rgument:

ϕ(g

· g

) = ϕ(g

) ⋆ ϕ(g

In such a case, the groups are called isomorphic.

DEFINITION 18.8 A map that preserves in this manner the group structure

is called an homomorphism or a group morphism; if it is bijective, it is a

group isomorphism.

Example 18.9 The set M o f matrices



1 x

0 1



with the product given by the product of matrices, is a group. Since M

· M

= M

x+ y

for any

x, y ∈ R, it follows that the (obviously bijective) map ϕ : x 7→ M

is a group isomorphism

between (R, +) and (M , ·).

Alternately, one speaks of a representation of the group G by G

′

if there

exists a homomorphism ϕ : G → G

′

(not necessarily bijective).

Example 18.10 Let U be the set of complex numbers z such t hat |z|= 1. The map ϕ : R → U

deﬁned by ϕ(θ) = e

iθ

is a group morphism between (R, +) and ( U, ·), but it is not an

isomorphism. Its kernel, deﬁned as the set of elements with image equal to the identity

element in U, is g iven by

Ker ϕ = {θ ∈ R ; ϕ(θ) = 1} = 2πZ.

The map ϕ : R → U is a (nonbijective) continuous representation

of the additive group R.

(Note th at the groups R and U have very different topological propertie s; for instance, R is

simply connected, whereas U is not.)

On the other hand, if we denote by G the group of rotations of R

centered at the

origin 0, th e map ψ : G → U which associates e

iθ

to a rotation with angle θ is indeed a group

isomorphism. M o reover, it is conti nuous. It follows that G, like U , is not simply connected.

By far the most us eful representations are those which map a group (G, ·)

to the group of a utomorphisms of a vector space or, equivalently, to the group

(K) of invertible square matrices of s ize n:

To speak of continuity, we must have a topology on each group, which h ere is simply the

usual topology of R and of U ⊂ C.

492 Groups and group representations

DEFINITION 18.11 Let K be either R or C. A linear representation of a

group G deﬁned over K is a pair (V , ϕ), where V is a K-vector space a nd

ϕ is a homomorphism of G into Gℓ(V ), t he group of linear automorphisms

of V.

Such a representation is of ﬁnite degree if V is a ﬁnite-dimensional vector

space, and the degree of the representation is the dimension n of V . In this

case, Gℓ(V ) is isomorphic to GL

(K), and we have a matrix representation.

By abuse of notation, one sometimes refers to V only, or to ϕ only, as a

representation of the group G.

DEFINITION 18.12 Let (V , ϕ) be a linear representation of a G. This repre-

sentation is faithful if ϕ is injective, tha t is, if distinct elements of the group

have distinct images (this means no information is lost by going th rough t he

map ϕ).

On the other hand, the representation is trivial if ϕ(g) = Id

for any

g ∈ G, i.e., if we have ϕ(g)(v) = v for all g ∈ G and all v ∈ V (which means

all information in G is lost after applying ϕ).

Example 18.13 Consider Example 18.9 again. The map ϕ : R → GL

(R) which associates the

matrice M

to a real number x is a faithful matrix representation of R.

18.3

Vectors and the group S O(3)

In this section, physical space is identiﬁed with the vector space E = R

DEFINITION 18.14 The special orthogonal group or group of rotations of

euclidean space E = R

, denoted S O(E), is the group of linear maps R :

→ R

such that

• the scalar product is invariant under R:

∀a, b ∈ R

( a|b) =



R( a)



R( b)



;

• R preserves orientation in space: the image of any b asis which is posi-

tively oriented is also positively oriented.

The rotation group SO(E) will be identiﬁed without further comment with

the group S O(3) of matrices representing rotations in a ﬁxed orthonormal

basis.

Denoting by R the matrix representing a rotation R in the (orthonormal)

canonical basis of E, we have

( a|b) = (R a|R b) = ( a|

RR b) for all a, b ∈ E

Vectors and the g roup SO(3) 493

(using the invariant of the scalar product under R), which shows that R is an

invertible matrix and that

R = R

−1

. (18.1)

A matrix for w hich (18.1) holds is called an orth ogonal matrix.

Thus linear maps preserving the scalar product correspond to orthogonal

matrices, and they form a group, called the orthogonal group, d enoted O(E).

The group of orthogonal matrices is itself denoted O(3). Note that the matrix

−I

, although it is orthogonal, is not a rota tion matrix; indeed, it reverses

orientation, and its determinant is equal to −1.

The group O(3) is therefore larger than SO(3). More precisely, we have:

THEOREM 18.15 The group O(3) is not connected; it is the union of two connected

subsets, namely, SO(3) and {−R ; R ∈ SO(3)}, on which the determinant is equal,

respectively, to 1 and −1.

Since the identity matrix lies in SO(3), it is natural to state that SO(3) is

the connected component of the identity in O(3).

To summariz e, th e notation SO(3) means

“S” for special (i.e., with determinant 1),

“O” for orthogonal (such that

R = R

−1

Consider then a rotation R

θθ

, cha racterized by a vector θθ

θθ ∈ R

with norm

θ ∈ [0, 2π[ (the angle of the rotation), directed along a unit vector n (the axis

of the rotation): θθ

θθ = θ n.

Denote by (e

, e

) the basis vectors in space and by (e

′

, e

′

, e

′

) their

images by a rotation R

θθ

. With matrix notation (it is easy to come back to

tensor notation) we denote by R(θθ

θθ) the matrix deﬁned by the relations

′

j=1



R(θθ

θθ)



i j

Note : the matrix R(θθ

θθ) is not the matrix for the change of basis L

deﬁned Equation (16.1)

on page 434, but its transpose. Here, we have, symbolically,







′







= R(θθ

θθ)













which means that one can read the coordinates of the new vectors in th e old basis in the rows

of the matrix (rather than in the columns). The matri x linking the coordinates of a (ﬁxed)

point in both bases is R(θθ

θθ)

−1

R(θθ

θθ) :







′







R(θθ

θθ)













494 Groups and group representations

A rotation R(θ e

) with angle θ around the axis O z is represented by th e

matrix

(θ)

def

= R(θ e

) =







cos θ sin θ 0

−sin θ cos θ 0

0 0 1







Similarly, the matrices of rotations around the axis O x and O y are deﬁned

(ζ)

def

= R(ζ e

) =







1 0 0

0 cos ζ sin ζ

0 −sin ζ cos ζ







and (b e careful with the sign in this last formula!)

(η)

def

= R(η e

) =







cos η 0 −sin η

0 1 0

sin η 0 cos η







Remark 18.16 When speaking of space rotations, the re are two different points of view, for

a physicist. The ﬁrst point of view (called active) is one where the axes of the frame (the

observer) are immobile, whereas the physical system is rotated. In the sec ond point of view,

called passive, the same system is observed by two different observers, the axes of whose

respective frames differ from each other by a rotation. In all the rest of the text, we only consider

passive transformations.

For a rotation R(θθ

θθ) parameterized by θθ

θθ = θ n, we can express the vector θθ

θθ

in terms of the canonical basis:

θθ

θθ = ζ e

+ η e

+ θ e

How does one deduce the representation for the rotation R(θθ

θθ)? It is tempting

to try the product R

(ζ) · R

(η) · R

(θ); however, performing th e product in

this order seems an a rbitrary decision, and the example of the d omino on

page 490 should convince the reader that this is unlikely to be the correct

solution. Indeed, in neither the ﬁrst nor the second line is the ﬁnal state of

the domino the same as its state after a rotation of a ngle π/

2 around the

ﬁrst diagonal in the O x y-plane.

A proper solution is in fact quite involved. It is ﬁrst required to use

inﬁnitesimal transformations, that is, to consider rotations with a “very small”

angle δθ. Then it is necessary to explain how non-inﬁnitesimal rotations may

be reconstructed from inﬁnitesimal transformations, by means of a process

called “exponentiation” (which is of course related to the usual exponential

function on R).

Consider then a rotation with axis O z and “inﬁnitesimal” a ngle δθ: it is

given by

R(δθ e

) =







1 δθ 0

−δθ 1 0

0 0 1







= I

+ δθ J

Vectors and the g roup SO(3) 495

where we put

def

dR(θ e

)

dθ



θ=0







0 1 0

−1 0 0

0 0 0







Similarly, deﬁne

def

dR(ζ e

)

dζ



ζ=0







0 0 0

0 0 1

0 −1 0







and

def

dR(η e

)

dη



η=0







0 0 −1

0 0 0

1 0 0







DEFINITION 18.17 Denote J

= J

, J

= J

, and J

= J

. The matrices J

thus deﬁned are the inﬁnitesimal generators of rotations. We denote by J

the vector J = ( J

, J

How does one now pass from inﬁnitesimal t ransformations to “ﬁnite”

transformations?

A ﬁ rst method is to remark that the set of matrices of the

form R(θ e

) is a representation of the addit ive group (R, +), wha t is called a

one-parameter group,

since we have R



(θ + θ

′

) e



= R(θ e

) ·R(θ

′

). An

explicit computation shows that

dR(θ e

)

dθ



θ=θ







−sin θ

cos θ

−cos θ

−sin θ

0 0 1







= J

·R(θ

and hence the matrix-valued function R(θ e

) is a solution of the ordinary

differential equation with constant coefﬁcients

′

= J

· M

for w hich the solutions are given by

R(θ e

) = R(0)·exp(θ J

) = exp(θ J

) = I

+θ J

+···+

+··· .

(This series is absolutely convergent, and therefore convergent.) This is a

general fact, and the following theorem holds:

THEOREM 18.18 Let



R(θ)



θ∈R

be a one-parameter group of matrices. Then its

inﬁnitesimal generator given by J = R

′

(0) satisﬁes R(θ) = e

θ J

for any θ ∈ R.

“Finite” in the usual physicist’s sense, meaning “not inﬁnitesimal.”

I.e., a group with elements of the type g

, x running over the group of real numbers R,

such that g

· g

= g

y+x

and g

−x

= g

−1

for any x, y ∈ R.

496 Groups and group representations

Proof. Indeed, we have R(0) = I and

dR(θ)

dθ

= lim

h→0

R(θ + h) − R(θ)

= lim

h→0



R(h) −Id



R(θ) = J R(θ),

which shows that R(θ) is the solution of the differential equation with constant co ef-

ﬁcient R

′

= J R such that R(0) = I, that is, R(θ) = e

θ J

THEOREM 18.19 Let R

θθ

be a rotation characterized by the vector θθ

θθ = θ n (angle θ,

axis directed by the vector n). Then, denoting as before J = ( J

, J

), the matrix

representing R(θθ

θθ) is given by

R(θθ

θθ) = exp(θθ

θθ · J) = exp(θ

+ θ

It is important here to be very careful that the matrices J

do not commute

with each other, so that this expression is not a rotation with angle θ

around

the x-axis, followed by a rotation with angle θ

around the y-a xis, and a

rotation with angle θ

around the z-axis:

exp(θ

+ θ

) 6≡ exp(θ

) exp(θ

However, using the exponentials, the matrices J

can provide any rotation

matrix. Even better: it turns out that, in practice, it is only necessary to know

the commutation relations between the matrices J

. The reader will easily check

that they are given by

[ J

, J

] = −J

, [ J

, J

] = −J

, and [ J

, J

] = −J

(recall th at [A, B] = AB − B A for any two square matrices A and B), which

can be summarized neatly by the single formula

[ J

, J

] = −ǫ

i jk

, (18.2)

where summation over the repeated index (i.e., over k) is implicit, and where

the tensor ǫ is the totally anti-symmetric Levi-Civita tensor. The commutation

relations (18.2) deﬁne wha t is called the Lie algebra of S O(3). The coefﬁcients

−ǫ

i jk

are the structure constants of the Lie algebra of SO(3).

Remark 18.20 The minus sign in the formula is not important; if we had been dealing with

active transformations instead of p assive ones, the matrice s J

would have carried a minus sign,

and the commutation relations also.

Knowing the Lie algebra of the group (i.e., knowing the structure constants)

is enough to recover the local structure of the group. (However, we will see

that there exist groups wh ich are “globally” different but have the same Lie

algebra, for instance, SO(3) and SU(2), or more simply SO(3) and O(3); but

this is not a coincidence, s ince SU(2) is a covering of SO(3).)

Remark 18.21 Since SO(3) i s a group, performing a rotation with parameter θθ

θθ followed by a

rotation wit h parameter θθ

θθ

′

is another rotation, with parameter θθ

θθ

′′

. However, there is no simple

relation between θθ

θθ, θθ

θθ

′

and θθ

θθ

′′