Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

The group SU(2) and spinors 497

DEFINITION 18.22 Ob jects that are transformed by a matrix of SO(3) during

a passive rotation of coordinate axes a re called vectors. It is sometimes said

that SO (3) is the vector representation of the group of rotations.

Example 18.23 Consider a rotation R of R

. The differential of R at any point is dR = R,

which shows that velocit y vectors t ransform according to R. In other words veloci ty vectors

are indeed objects that transform according to a vector representation.

A vector, in the representation-theoretic sense here, is therefore more than

simply an element of a vector space: it is an object generating the representa-

tion SO(3) of the rotation g roup [18, 28].

18.4

The group S U(2) and spinors

Consider now the complex vector space E

′

= C

, with its canonical

Hilbert structure, that is, with the hermitian scalar product

( x|y) =

x · y = x

+ x

, wh ere x =





and y =





DEFINITION 18.24 The special unitary group of E

′

, denoted S U(E

′

), is the

group of linear maps from E

′

to itself which preserve the scalar product and

have determinant one.

If M is the matrix representing such a linear map in the canonical basis,

we have therefore:

( x|y) = (M x|M y) =

(M x) · M y =





M M y



for any x, y ∈ E

′

, wh ich implies that

M M = I

DEFINITION 18.25 The conjugate transpose of a matrix M is denoted

†

def

A matrix such that M · M

†

= I

only also satisﬁes

|det M|

= det M ·det

M = det(M · M

†

) = 1.

Such a matrix is a unitary matrix. Its determinant is of the form e

iα

for

some real number α.

Example 18.26 The matrix M = diag(e

iα

, e

iβ

) is unitar y, but does not belong to SU(2) if

α + β 6≡ 0 mod 2π.

498 Groups and group representations

DEFINITION 18.27 The group of complex 2 by 2 matrices such that

M · M

†

= I

and det M = 1

is denoted S U(2).

The notation SU(2) comes f rom

“S” for special (i.e., with determinant 1),

“U” for unitary (i.e., with

M = M

−1

Recall that any rotation matrix could be expressed as the exponential of a

linear combination of elementary matrices J

; a similar phenomenon holds

for matrices in SU(2). First, notice that any matrix in SU(2) is of the form

U =



α β

−β α



with |α|

+ |β|

= 1.

 Exercise 18.1 Prove this property.

If we write α = a + ib and β = c + id, it follows therefore that a

+ c

+ d

= 1. We can write a = cos(θ/2) for some θ and then write

(b, c, d) = sin(θ/2)n, where t he real vector n = (n

, n

) is of norm one.

Then U is given by

U (θθ

θθ) =



cos





i sin



n ·σσ

σσ,

where

σσ

def

= (σ

, σ

the matrices σ

being none other than the Pauli matr ices , well known to

physicists:



0 1

1 0





0 −i

i 0





1 0

0 −1



Those matrices h ave trace zero (th ey are “traceless” in the physicist’s language)

and are her mitian, which means that we have

†

= σ

for i = 1, 2, 3.

The Pa uli matrices play for SU(2) the same role that th e J

play for SO(3), as

we will see. First, notice that the reasoning above can be reversed:

PROPOSITION 18.28 Let θθ

θθ = θ n be a vector in R

. The matrix θθ

θθ·σσ

σσ is hermitian,

and the matrix U (θθ

θθ) = e

iθθ

θθ·σσ

σσ/2

is unitary. Moreover, we have

U (θθ

θθ) = (cos θ/2) I

+ (i sin θ/2) n ·σσ

σσ

cos

+ in

sin

(in

+ n

) sin

(in

−n

) sin

cos

−in

sin

The group SU(2) and spinors 499

Proof. A direct computation shows that U (θθ

θθ) ·

U (θθ

θθ) = I

PROPOSITION 18.29 (Properties of the Pauli matrices)

Commutation relations:



iσ



= −ǫ

i jk

iσ

;

Anticommutation relations:

+ σ

= 2 δ

i j

= δ

i j

+ iǫ

i jk

tr (σ

) = 0, σ

†

= σ

The groups SO(3) and SU(2) are quite similar. Indeed, for any vector

θθ

θθ ∈ R

, we construct t wo matrices

R(θθ

θθ) = exp(θθ

θθ · J) ∈ SO(3) and U (θθ

θθ) = exp(iθθ

θθ ·σσ

σσ/2) ∈ SU(2),

using the matrices ( J

, J

) and (σ

, σ

), respectively, which satisfy the

same commutation relations:

[ J

, J

] = −ǫ

i jk

and



iσ



= −ǫ

i jk

iσ

The structure constants of SO(3) and SU(2) are identical. Since these structure

constants are enough to reconstruct (locally) the internal product law of the

group, there should e xist a strong link between the groups. This is made

precise by the following theorem:

THEOREM 18.30 The group SO(3) is a representation of SU(2): there exists a

homomorphism

R : SU(2) −→ SO(3),

U 7−→ R

Moreover, for any U ∈ SU(2), the matrices U and −U have same image: R

−U

Proof. We need a way of constructing a matrix R

∈ SO(3) for any matrix U ∈

SU(2), such that the group structure is preserved. In other words, we need that

·R

= R

U V

for al l U , V ∈ SU(2).

A trick is needed to do this. Denote by

M =



M ∈ M

†

= M, tr M = 0}

the vector space of hermitian matrices with trace zero. This may be written

M =

¦

z x−i y

x+i y −z



; x, y, z ∈ R

= {x ·σσ

σσ ; x ∈ R

Thus, for any vector x = (x, y, z) ∈ R

, we have a unique associated matrix in M ,

denoted M ( x) = x ·σσ

σσ.

500 G roups and group representations

LEMMA 18.31 For all x, y ∈ R

, we have

x · x

′



M( x) M( x

′

)



and det M( x) = −x

Conversely, any matrix M ∈ M can be written M =

with x

tr (M σ

Proof of the lemma. This is a simple computation.

Now we can describe the construction of the map U 7→ R

Let U ∈ SU(2 ). We look for a matrix R

, that is, a rotatio n matrix, which we may

characterize by its action on R

. Si nce M ≃ R

, we may start by ﬁnding a matrix

acting on M . For this purpose, deﬁne

Q(U ) : M −→M ,

M 7−→ U M U

−1

First notice t h at obviously we have Q(−U ) = Q(U ) for all U ∈ SU(2). It is also

simple to check that M

′

= U M U

−1

is also in M : indeed, we have

†

= (U M U

−1

)

†

= (U M U

†

)

†

= M

and

tr M

′

= tr (U M U

−1

) = tr M = 0.

Hence there ex ists a unique element x

′

∈ R

such that M

′

= x

′

·σσ

σσ. We then deﬁne

′

= R

( x), and in this manner we have deﬁned a map R

: R

→ R

. The

uniqueness of x

′

implies that R

is linear.

LEMMA 18.32 R

is a rotation.

Proof of the lemma. We compute the norm of x

′

: we have

= −det M

′

= −det(U M U

−1

) = −det M = x

and hence R

is an isometry. I t is therefore in O(3). We may c o mpute the

coefﬁcients of R

, remarking that the vector x = (x

)

is mapped to x

′

= (x

′

)

with

′

tr (M

′

) =

tr (U M U

−1

) =

tr (U x

−1

)

tr (U σ

−1

) x

)

i j

tr (σ

U σ

−1

A direct computati o n shows ﬁnally that we have det R

> 0; hence R

is a

rotation.

To conclude, we check now that for any M ∈ M , we have



Q(U ) ◦ Q(V )



(M ) = U (V M V

−1

= (U V ) M (U V )

−1

= Q (U V )(M),

showing that Q(U ) Q(V ) = Q (U V ) for any U , V ∈ SU(2) and therefore that U 7→

Q(U ) is a homomorphism. It also satisﬁes Q (−U ) = Q(U ). This implies th at

these propertie s are also valid for the map U 7→ R

(this may be checked usi ng the

coefﬁcients (R

)

i j

computed above).

Here is a summary of the course of the proof:

The group SU(2) and spinors 501

R θθ

θθ = θ n M (θθ

θθ) = θθ

θθ ·σσ

σσ U = exp (iθθ

θθ ·σσ

σσ/2)

rotation vector matrix in M matrix in SU(2)

(θ deﬁned up to 2π) θθ

θθ =

tr (Mσσ

σσ) (θ deﬁned up to 4π)

In other words, any element of SU (2) may be mapped to an element

in SO(3). However, this representation is not faithful: different elements

of SU(2) can have th e same image in SO(3); indeed this is the case for U and

−U which have the s ame associated represent ation (this is the only case where

this happens). In other words, there is no inverse to this homomorphism (it

would be “bi-valued”).

In fact, there is no continuous isomorphism b etween SO(3) and SO(2)

because these two spaces are not topologically equivalent:

THEOREM 18.33 SO(3) is not simply connected, but is doubly connected (i.e.,

running twice ov er any closed path gives a path which is homotopic to a point).

On the other hand SU(2) is simply connected.

Proof (intuitive). We will explain why SO(3) is not simply connected. Any element

R ∈ SO(3) may be characterized by a unit vector n, deﬁning the axis of rotation, and

by its angle θ, as before, and R is parameterized again by the vector θ n. This is a

continuous parameterization, so the group SO(3) may be represented by a sphere with

radius π (any rotation of angle between π and 2π is also a rotation with angle θ [0,π]

and vector −n).

This is an exact description, up to one small detail: th e rotations (n, π) and (−n, π)

are equivalent. The group SO(3) is t herefore, topologically, the “same” as the following

space: a sph ere of radius π on the surface of which diametrically opposite points have been

identiﬁed.

Hence the ﬁgure below represents a closed path in SO(3). It is indeed closed since

the nort h and south poles of the sphere are identiﬁed, that is, they represent the same

point in SO( 3). The reader will easily convince herself that this closed path cannot be

continuously deformed into a single point (if we try to move the north pole toward

the south pole, the south pole is o bliged to also move to remain opposite).

On the other hand, suppose we travel along this path twice. Then the resulting path

may be co ntracted to a si ngle point, following the sequence of movements below (in

the ﬁrst ﬁgure, the path taken twice is also drawn twice for legibility):

502 Groups and group representations

Note, moreover, that a closed path in SU(2) may be represented as a closed path

that is repeated tw ice in SO(3).

A consequence of this theorem is th at a rotation of 4π is always equivalent

with a triv ial rotation for a physical object.

What is this useful for?

You may perform the following magic trick. Take any object (a rectangular

pencil eraser, for instance), and att ach at least t wo pieces of string to it. Then

attach the pieces of str ing to th e walls, ﬂoor, or ceiling of the room where you

are operating. Then turn the eraser once (a 2π-rotation). The strings become

entangled. Without cutting a string or turning the eraser again, it is impossible to

disentangle them and bring them back to their original state. However, if you turn

the eraser once more (another 2π-rotation, so altogether a 4π-rotation), it will

now be perfectly possible — in front of an admiring and disbelieving audience

— to disentangle t he strings without any more turns or cutting (see sidebar 7,

page 506).

This shows that rotat ing the eraser twice (4π-rotation) is equivalent to no

rotation at all, whereas one turn (2π-rotation) is not.

But shouldn’t a 2π-rotation be, in fact, equivalent with a zero rotation, a s is

commonly stated and believed? It all depends on the object considered. If, as

in th is trick, the object is not by itself, the answer is “No.” More generally, t he

mathemat ical properties of the object will reﬂect the path followed in SO(3)

to perform the rotation. In other words, the laws of the transformation must

reﬂect the group structure involved; but such a law is not unique: a physical

object may follow the trivial representa tion of SO(3) (it is then a scalar, such

as temperature), or a vector representation (it is then a vector, such as velocity);

a complex object may follow a representation of SU(2).

This is, for instance, the case of the wave function of the electron.

An electron may be represented (in nonrelativistic quantum mechanics) by

a wave function with two components,

Ψ( r, t) =



ϕ( r, t)

ψ( r, t)



During a rotation, this changes according to a spinorial transformation:

Ψ( r, t) 7−→ Ψ

′

( r

′

, t) =



′

( r

′

, t)

′

( r

′

, t)



= e

−iθθ

θθ·σσ

σσ/2



ϕ( r, t)

ψ( r, t)



, (18.3)

where θθ

θθ = θ n is the vector characterizing the rotation. Note that, as s een

previously, we have

−i(θ+2π) n·σσ

σσ/2

= −e

−iθ n·σσ

σσ/2

but

−i(θ+4π) n·σσ

σσ/2

= +e

−iθ n·σσ

σσ/2

Hence, a 4π-rotation is required in order that the wave function remain in-

variant. How is it, then, that this particular behavior of the electron (it is not

Spin and Riemann sphere 503

invariant under a 2π-rotation) has no consequence in physical observations?

After all, electrons exist abundantly in everyday matter. Note that, in fact, af-

ter a 2π-rotation, only th e sign of the wave function has changed; consequently,

the physical properties of the particle are unchanged. What changes are prop-

erties of interactions of th e particles: in particular, t he fact that electrons

are fermions (and hence obey the Pauli exclusion principle, so that matter is

stable) derive from this fact.

An object t ransforming according to the rule (18.3) is called a spinor.

Exercise 18.3 s hows tha t other transformation rules are poss ible.

Remark 18.34 The fact t h at SU(2) is like “twice SO( 3)” (or, more technically, it is a “double

cover” of SO(3)) is used to show that two states of spin e xist in the fundamental spinor rep-

resentation. In special relativity, the group of isometries of space is not SO(3) anymore, but

rather the group SO(3, 1) , that leaves Minkowski space (R

with the Minkowski metric) invari-

ant. One can show that there exists a si mply connected double cover of this group, isomorphic

to SL(2, C) and generated by two independent representations of SU(2) (one sometimes ﬁnd

the notation SU(2) ⊗ SU(2) to recall this independance). This is constructed using suitable

linear combinations of generators of rotations and Lorentz boosts as inﬁnitesimal generators.

This group then affords four degrees of freedom for a particle with spin

, instead of the two

expected; this allows us to predict that not only the particle is thus described, but so is the

associated antiparticle.

The reader interested by the mathematics underlying the representations of the Dirac equa-

tion may begin by looking at the excellent book [68].

18.5

Spin and Riemann sphere

While we are dealing with pretty pictures, I will not resist the temptation

to present an application to quantum mechanics of the representation of the

complex plane as the Riemann sphere (see page 146); more precisely, this

concerns the representation of the spin.

We know that th e wave function of an electron (or indeed of any other

particle with spin

) may be represented as the tensor product of a vector |f 〉

corresponding to a space dependency and a vector |χ〉 corresponding to the

spin:

|Ψ〉 = |f 〉⊗|χ〉.

This is another way of e xpressing that th e wave function has two components,

as in (18.3) (the ﬁrst, ϕ, corresponding to the sta te |↑〉 or “spin-up,” and the

second, ψ, corresponding to the state |↓〉 or “spin-down”).

Let us concentrate only on the spin for now. Then the wave function |χ〉

is a linear combination of the basis vectors |↑〉 and |↓〉. This, however, is

related to the choice of one particular direction for the measure of the spin,

namely, the direction z. We might as well have chosen another direction, for

504 Groups and group representations

instance, the direction x. Any vector |χ〉 would then be a linear combination

of |→〉 and |←〉, eigenvectors for the measure of spin on the x axis.

How is a wave function (denoted |ր〉) characterized w hen it is an eigen-

vector for the measure of spin in an arbitrarily chosen direction? Since the

family



|↑〉, |↓〉



is a basis of the space of spins, there exist complex num-

bers λ, µ ∈ C such that

|ր〉 = λ |↑〉+ µ |↓〉.

Because the physical meaning of a wave function is not changed when the

vector is multiplied by an arbitrary nonzero complex number, it follows that

only the ratio λ/µ is necessary to characterize the state |ր〉.

Then we have the following very nice result:

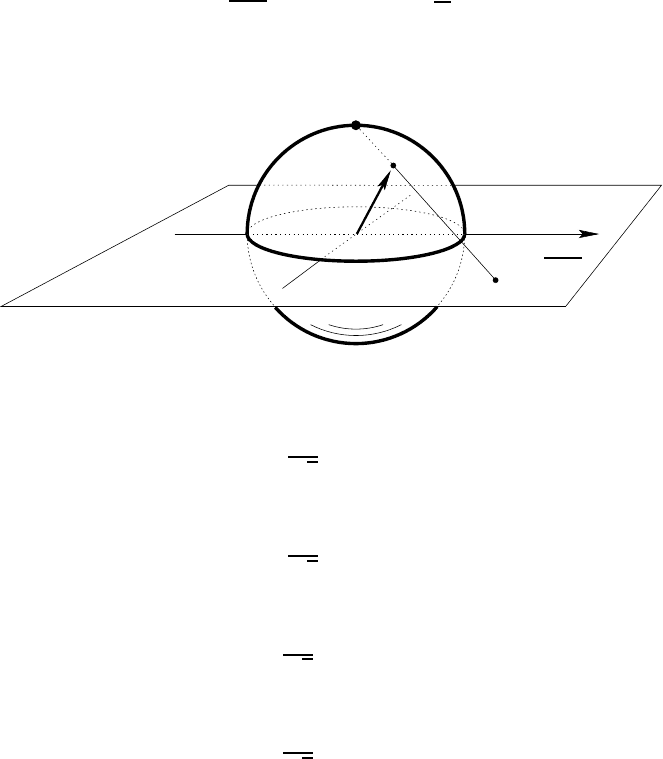
THEOREM 18.35 Let z = λ/µ; then we have z ∈ C = C ∪ {∞}. The stereo-

graphic projection z

′

of z on the Riemann sphere gives the direction characterizing the

vector |ր〉.

′

1−1

−i

z = λ/µ

∞

For instance, to obtain the direction of positive x, we should take z = 1,

which gives (after normalizing appropriately):

|→〉

|↑〉+ |↓〉

To obtain t he direction (−O x), we must ta ke z = −1:

|←〉

|↑〉−|↓〉

For the direction (O y), we take z = i:

|→〉

|↑〉+ i |↓〉

Similarly, for the direction (−O y), we take z = −i:

|←〉

|↑〉−i |↓〉

Exercises 505

Finally, for direction (O z), we must of course take z = ∞:

|↑〉= |↑〉+ 0 |↓〉,

whereas the direction (−O z) corresponds to z = 0, so:

|↓〉= 0 |↑〉+ |↓〉.

EXERCISES

 Exercise 18.2 Let σ

(i = 1, . . . , 3) denote the Pauli matrices. For a real number γ, compute

exp (−iγσ

/2) ·σ

·exp (iγσ

/2) when k = 1, 2, 3. Interpret this result.

 Exercise 18.3 (Rotations acting o n functions) Let R be a rotation. To a smooth funct ion

ψ( r), we associate the function Rψ such that Rψ( r) = ψ



−1

( r)



(so that th e axes have been

transformed by the rotation R). For a rotation R

(θ) around the O z-axis, show that we have

(δθ)ψ(x, y, z) = ψ(x − y δθ, y + x δθ, z) and then that

(θ)

dθ

ψ = i L

(θ) ψ with L

= −i



∂

∂ y

+ y

∂

∂ x



Deduce that R

(θ) = exp(iθL

) and generalize this to the other axes. Show that

[iL

, iL

] = −ǫ

i jk

506 Groups an d group representations

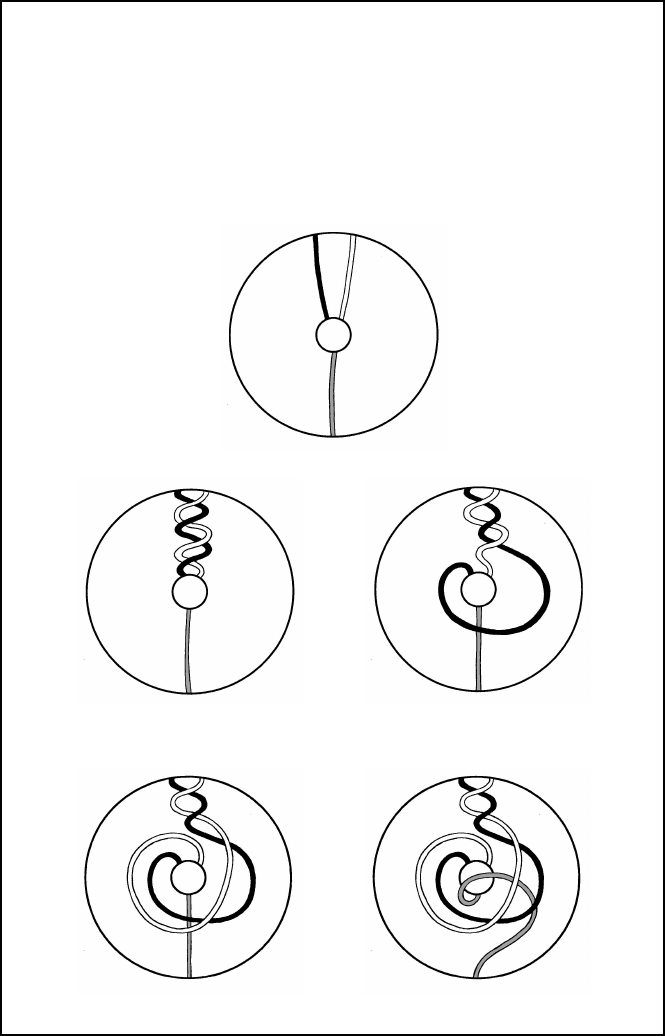
Sidebar 7 (Double connectedness of S O(3) and magic tricks) Start with a

sphere attached to the ceiling and ﬂ oor with three strings (or more). At the beginning

of the experiment, the sphere is rotated by an angle of 4π (i.e., turned twice completely);

hence the strings that attach it become entangled. However, without turning the sphere

anymore, and of course without putting knife or scissors to the str ings, it is possible to free

the strings, following the sequence below, at the end of which all the strings are exactly as

they where before the rotation was performed.

(It is necessary to assume that the strings are some what ﬂexible; all this is topological,

that is, it requires continuous deformation.)

Initial positon.

After two rotations of the sph ere, the

strings are entangled.

Beginning of the trick .

The white string goes over the rest. The gray string starts moving.