Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

Conditional probability 517

19.4

Conditional probability

 Exercise 19.1 You’re taking a plane to Se attle. A colleague tells you: “There is a one in ten

thousand chance that there is a bomb in a plane. But there is only one in a hundred million

chance that there are two bombs. So, for more security, just bring your own bomb.”

What should you think of this argument?

DEFINITION 19.19 Let A and B be two events such th at P(B) 6= 0. The

conditional probability of the event A knowing the event B is the quantity

(A) = P(A|B) =

P(A ∩ B)

P(B)

It is denoted either P

(A) or P(A|B).

Example 19.20 The probability that there are two bombs in your plane, knowing that there is

at least one (yours) is therefore simply one in ten thousand. Bringing one in your luggage is a

useless precaution.

If P(A) 6= 0 as well as P(B) 6= 0, it is also possible to deﬁne th e probability

of B knowing A. Then we have

P(A ∩ B) = P(B) ·P(A|B) = P(A) ·P(B|A),

hence the following formula, due to the clergyman T homas Bayes, who pub-

lished it in 1764 [12]:

THEOREM 19.21 (Bayes formula ) Let A and B be two events in Σ with nonzero

probability. Then we h ave

P(B|A) =

P(A|B) ·P(B)

P(A)

Although it is very simple, this is an interesting result since it relates

the probability that the event B is realized knowing A to the “reciprocal”

probability tha t A be realized knowing B. One has to be careful because

those two quantities are often confused, either knowingly or unknowingly.

For instance, a scary message such as “95% of heroin addicts started by

smoking marijuana” may be used with the intent of suggesting (without stat ing

it explicitly) that “95% of smokers of marijuana become heroin addicts.” This

is the ordinary fare of most political campaign arguments, of advertisements

of every kind, and those never-ending polls.

But the greatest care is necessary, as the following example shows:

518 Introduction to probability theory

Thomas Bayes (1702—1761), English Presbyterian minister and the-

ologian, studied mathematics, and in part icular probability theory,

during his free time. He published little of his work during his

lifetime and remained unknown to most of his peers. His Essay

towards Solving a Problem in the Doctrine of Chances was published

posthumously in 1764.

Example 19.22 On the planet Zork live two ethnic groups: Ents and Vogons. According to a

recent statistical analysis of th e distribution of wealth on Zork, it is true that

• 80% among the Vogons are poor • 80% among the poor are Vogons.

Is it possible to deduce that wealth is inequitably distributed between the two groups?

◊ Solution: Cer tainly not, in the absence of othe r data such as the proportion

of Vogons in the population. It may very well be the case that the Vogons

represent 80% of the total population, and that 80% of the total population is

poor. If that is the case, wealth is equitably distributed between the t wo groups

(not necessarily within each group). Again, this kind of confusion occurs

continually, and is sometimes encouraged. (Many ex amples can be found by

reading almost any newspaper, adapting the two words “poor” and “Vogons”

to various circumstances.)

We now introduce a minor generalization of a complete system, which

allows the events in the system only to cover the sample space up to a set of

probability zero.

DEFINITION 19.23 An almost complete system is a sequence (A

)

n∈N

events in Σ such that

i) A

∩ A

= ∅ if m 6= n,

ii) P



n∈N



= 1.

THEOREM 19.24 (Bayes formula ) Let (A

)

n∈N

be an almost complete system of

events, and let B be an arbitrary event B ∈ Σ. Assume that P(A

) > 0 for any

n ∈ N. Then we have

i) P(B) =

n∈N

P(B|A

)P(A

);

ii) if, moreover, P(B) > 0, then

∀p ∈ N P(A

|B) =

P(B|A

) ·P(A

)

n∈N

P(B|A

) ·P(A

)

Independent events 519

Remark 19.25 The Collins case is a striking example of the use (or misuse) of probability and

conditional probability. In Los Angeles i n 1964, a blond woman and a black man with a beard

were arrested for a robbery. Despite the absence of convincing evidence, the prosecution argue d

successfully that they must be guilt y because the chance that a random couple corresponded (as

they did) to the w itness’s description was estimated to be one in twelve million. The California

Supreme Court reversed th e judgment on appeal, since it was shown that the probability that

at least two couple s in the Los Angeles area correspond to the description knowing that at least

one couple does (namely, the actual thieves) was close to 4 2 %, and therefore far from negligible

(certainly too large to decide guilt “beyond reasonable doubt”!). This shows t h at there was a

high probability that arresting the co u ple was a mistake.

19.5

Independent events

It is now time to deﬁne the notion of independent events. Intuitively, to

say that two events A and B a re independent means tha t the probability that

A is realized is equal to th e probability that it is realized knowing th at B is

realized, or indeed to the probability that A is realized know ing th at “not-B”

is realized.

DEFINITION 19.26 Let A and B be two events in Σ. Then A and B are

independent if P(A ∩ B) = P(A) P(B), or, equivalently if 0 < P(B) < 1, if

P(A|B) = P(A|∁B) = P(A).

Let Σ

, . . . , Σ

be σ-algebras contained in Σ. They are independent σ-

algebras if

∀(B

, . . . , B

) ∈ Σ

×···×Σ

, P



i=1



i=1

P(B

Moreover, events A

, . . . , A

are independent if the σ-algebras

σ({A

}), . . ., σ({A

})

are independent.

Warning! The pairwise independence of events A

,. . . , A

does not imply

their independence. In fact, we have the following result:

THEOREM 19.27 The events A

, . . . , A

are independent if and only if, for any

p ∈ N, p ¶ n, and for any p-uple of distinct indices (i

, . . . , i

), we have



k=1



k=1

P(A

In p articular, for n = 2, we recover the ﬁrst deﬁnition: A and B are independent

events if and only if P(A ∩ B) = P(A) P(B).

520 Introduction to probability theory

Example 19.28 Consider the experiment of rolling two dice, and the events:

• event A: the sum of t he results of both dice is even;

• event B: the result of the ﬁrst die is even;

• event C: the result of the second die is e ven.

It is easy to check that A, B, and C are pairwise independent. Indeed, we have (assuming all

36 outcomes of the experiment have probability 1/36):

P(A) = P(B) = P(C ) =

whereas P(A ∩ B) = P(B ∩ C ) = P(C ∩ A) =

On other hand, A, B, C are not independent, since

P(A ∩ B ∩ C ) = P(B ∩ C ) =

whereas P(A) P(B) P(C ) =

(This is also clear intuitively, si nce A and B together imply C , for instance.)

One should note tha t t his concept of independence depends only on a

numerical evaluation of probabilities , and that it may turn out to be in contra-

diction with common sense or intuition, for which independence may carry

deeper meaning. In particular, independence should not be mistaken with

causality (see Section 20.11, page 550).

Chapter

Random variables

Falstaff. Prith ee, no more prattling; go. I’ll hold.

This is the third ti me; I hope good luck lies in odd numbers.

Away I go. They say there is divinity in odd numbers,

eithe r in nativity, chance, or death. Away!

William Shakespeare

The Merry Wives of Windsor, Act V, Scene i.

As we have noticed in the previous chapter, the sample space Ω is not

usually a mathematically simple set — it may well be a population of exotic

ﬁshes, a collection of ideas, or representatives of various physical measure-

ments. Worse, this set Ω is often not known. Then, instead of working with

the probability measure P on Ω, one tries to reduce to various probabilities

on R.

For this purpose, we consider a map X from Ω to R (which is called

a random variable); R becomes the new set on which a measure is deﬁned.

Indeed, a probability measure denoted P

, which is the “ image” of P by X ,

and which is called the probability distribution of X , is deﬁned.

20.1

Random variables and probability distributions

DEFINITION 20.1 Let (Ω, Σ) be a probability space. A random variable is a

function X , deﬁned on Ω and with values in R, which is measurable when R

522 Ran dom variables

is equipped with the Borel σ-algebra, that is, such that we have X

−1

(A) ∈ Σ

for any Borel set A ∈ B(R).

To simplify notation, we will abbreviate r. v. instead of writing “random

variable.”

A “random” function is, in other words, simply a measurable function —

and, for a physicist not overly concerned with quoting the axiom of choice,

this means “any function” that she may think about.

Here is an example. Take as probability space

Ω

def

= {all students at Rutgers university},

with the σ-algebra Σ = P(Ω).

We can deﬁne a random variable X corresponding to the “age” of a stu-

dent:

X (student) = age of the student ∈ R.

Now we can study the distribution of the age in the population (evaluate

the average, the standard dev iation,...) without knowing too much about Ω,

which can be a rather complicated set to envision precisely (if we think that

it contains information such a s the fact that François prefers to sing Bach in

B-ﬂat, or that Winnie’s preferred dessert is strawberry cheesecake).

Given a probability space (Ω, Σ, P) a nd an r.v. X on Ω, the probability

distribution of X is deﬁned as the image probability measure of P by X :

DEFINITION 20.2 (Distribution) Let (Ω, Σ, P) be a probability space and X

a random variable. The probability distribution of X is the probability

measure

: B −→ R

B 7−→ P{X ∈ B},

where

{X ∈ B}

def

= X

−1

(B) =



ω ∈ Ω ; X (ω) ∈ B



In particular, we have



]a, b]



= P{a < X ¶ b} = P



−1



]a, b]





= P





ω ∈ Ω ; a < X (ω) ¶ b





Note that this probability measure is in general deﬁned on a nother set

(R) and with respect to anoth er σ-algebra (of Borel sets) than that of the

probability space itself (Ω).

The following diagram summarizes this discussion:

Random variables and probability distributions 523

(unknown set) Ω

R R

(unknown)

(known)

In the example of the Rutgers students, assume moreover that the sample

space is given the uniform probability measure (ea ch student is given the same

probability, p = 1/N, where N is the tota l number of students). What is the

probability distribution of the random variable “ age,” which we see as integer-

valued? This distrib ut ion is a probability measure on the set N, an inst ance

of what is often called a discrete distribution:



{n}



= P



{X = n}



= P



{students ; age (student) = n}



number of students aged n

It can very well be the case that t wo random variables have the same

distribution without b eing closely related to each other. For instance,

THEOREM 20.3 Let X and Y be two random variables deﬁned on the same sample

space which are equal almost everywhere. Then X and Y have the same distribution:

= P

But be warned that the converse statement is completely false.

Consider, for example, t he process of ﬂipping n times a fair (unbiased)

coin, using 0 and 1 to denote, respectively, “head s” or “tails.” We can take

Ω = {0, 1}

and of course Σ = P(Ω). Let ω = (E

, . . . , E

) ∈ Ω, where

∈ {0, 1} for i = 1, . . ., n, be an atomic event. The probability of {ω} ∈ Σ,

if the successive throws are independent, is equal to



{ω}



= (1/2)

(uniform probability).

Consider now the random variable

X : Ω −→ N,

ω 7−→

i=1

= number of “tails.”

We can ﬁnd the distribution of X by denoting, for instance, A

the event

corresponding to “k tails out of n throws.” So A

∈ Σ and in fact



ω ∈ Ω ; X (ω) = k



The distribution of X is supported, in the case considered, on the set {0, . . . , n},

and we have



{k}



= P(X = k) = P(A

) =









524 Ran dom variables

This distribut ion is called the binomial distribution, and it is often denoted





. Note that it is easily checked that

(N) =

k=0





(1 + 1)

= 1,

as it should be. Moreover, it is easily seen th at if X has a binomial distribu-

tion, so d oes (n − X ) (corresponding to the number of “heads” in n throws).

Of course, X and (n − X ) are not equal almost everywhere!

What is clearly visible from this example is that distributions of random

variables only provide some information on the full sample space, by no means

all. This is the price to pay for t he simpliﬁcation that results from their use.

Whatever is not encoded in the random varia ble (all the factors lead ing to a

student of a certain a ge and not another, the exact trajectory in space of the

falling die...) is completely forgotten.

DEFINITION 20.4 (Bernoulli distribution, binomial distribution) Let n ∈ N

and p ∈ [0, 1]. A random variable X follows the Bernouilli distribution

with parameter p, denoted BB

BB(1, p), if



{1}



= p and P



{0}



= 1 − p.

A random variable X follows the binomial distribution BB

BB( n, p) if



{k}







(1 − p)

n−k

for k ∈ [[1, n]].

The binomial distribution B(n, p) corresponds to the sum of n indepen-

dent random var iables, each of which has a Bernoulli distribution with the

same parameter B(1, p).

20.2

Distribution function and probability density

DEFINITION 20.5 The distribution function of an r.v. X is the function

deﬁned for x ¾ 0 by

F (x)

def

= P



{X ¶ x}



= P



X ∈ ]−∞, x]



For all a, b ∈ R, we have



{a < X ¶ b}



= F (b) − F (a).

Distribution function and probability density 525

Since the σ-algebra of Borel subsets of the real line is generated by the

intervals ]−∞, a], the folowing result follows:

PROPOSITION 20.6 Let (Ω, Σ) be a probability sp ace. A map X : Ω → R is a

random variable if and only if X

−1



]−∞, a]



∈ Σ for all a ∈ R.

Moreover, the probability distribution P

is u niquely determined by the values



−1

(]−∞, a])



= F (a) for a ∈ R, that is, by the distribution function.

All information conta ined in the probability distribution P

is contained

in the distribution function F . The distribution function is t hus a funda-

mental tool of probability theory.

 Exercise 20.1 Express P



{a < X < b}



, P



{a ¶ X ¶ b}



, and P



{a ¶ X < b}



in terms

of F (b), F (a), F (b

−

), and F (a

−

From the deﬁnition of the distribution function, we immediately derive

the following theorem:

THEOREM 20.7 Let X be a random var iable with distribution function F. Then

F has the following properties:

i) F is right-continuous; that is, for all x ∈ R, we have

F (x

)

def

= lim

ǫ→0

F (x + ǫ) = F (x) ;

ii) F is not necessarily left-continuous, and more precisely we h ave

F (x) − F (x

−

) = P{X = x};

iii) for all x ∈ R, we have 0 ¶ F (x) ¶ 1 ;

iv) F is increasing ;

v) if we deﬁne

F (−∞)

def

= lim

x→−∞

F (x) and F (+∞)

def

= lim

x→+∞

F (x),

then

F (−∞) = 0 and F (+∞) = 1 ;

vi) F is continuous if and only if P{X = x} = 0 for all x ∈ R. Such a

probability distribution or random variable is called diffuse.

Proof. Only i) and ii ) require some care. First, write F (x + ǫ) − F (x) = P{x <

X ¶ x + ǫ}, then notice th at, as ǫ tends to 0 (following an arbitrary sequence), the set

{x < X ¶ x + ǫ} “tends” to the empty set which has measure zero. This proves i).

Moreover, writing F (x) −F (x −ǫ) = P{x −ǫ < X ¶ x}, one notices similarly that

the set {x −ǫ < X ¶ x} “tends” to {X = x}.

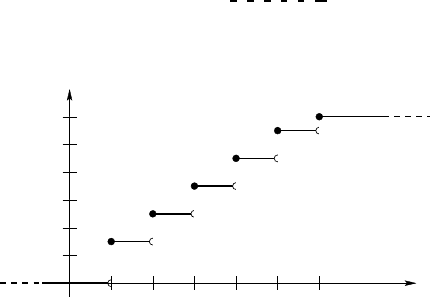
526 Random variables

20.2.a Discrete random variables

DEFINITION 20.8 Let (Ω, Σ, P) be a probability space. A random variable X

on Ω is a discrete random variable if X (Ω) is almost surely countable, that

is, there is a countable set D s uch that P{X /∈ D} = 0.

When an r.v. is discrete, it is clear that its distribution function has

discontinuities; it is a step function.

Example 20.9 Consider the e xperience of th rowing a weighted die, which falls on the numbers

1 to 6 with p robabilities respectively equal to

(this is the one I hand to my

friend Claude when playing with him).

The distribution funct ion of the corresponding random variable is given by the following

graph:

1 2 3 4 5 6

1/6

2/6

3/6

4/6

5/6

20.2.b (Absolutely) conti nuous random variables

DEFINITION 20.10 A random variable is continuous if its distribution func-

tion is continuous.

Remark 20.11 In fact, we should not speak simply of continuity, but rath er of a similar but

stronger property called absolute continuity. The reader is invited to look into a probability

or analysis book such as [83] for more details.

Since, for distribution functions, continuity and absolute continuity are in fact equivalent,

we will continue writing “continuous” instead of “absolutely continuous” for simplicity.

DEFINITION 20.12 The probability dens ity of a continuous r.v. with distri-

bution function F is a non-negative function f such that for all x ∈ R we

have



{X ¶ x}



= F (x) =

−∞

f (t) dt.

The density probability is almost everywhere equal to the derivative of F .

For a discrete r.v., the probability density f does not exist as a f unction, but

it may be represented with Dirac distributions, since we want to differentiate

a discontinuous function.