Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

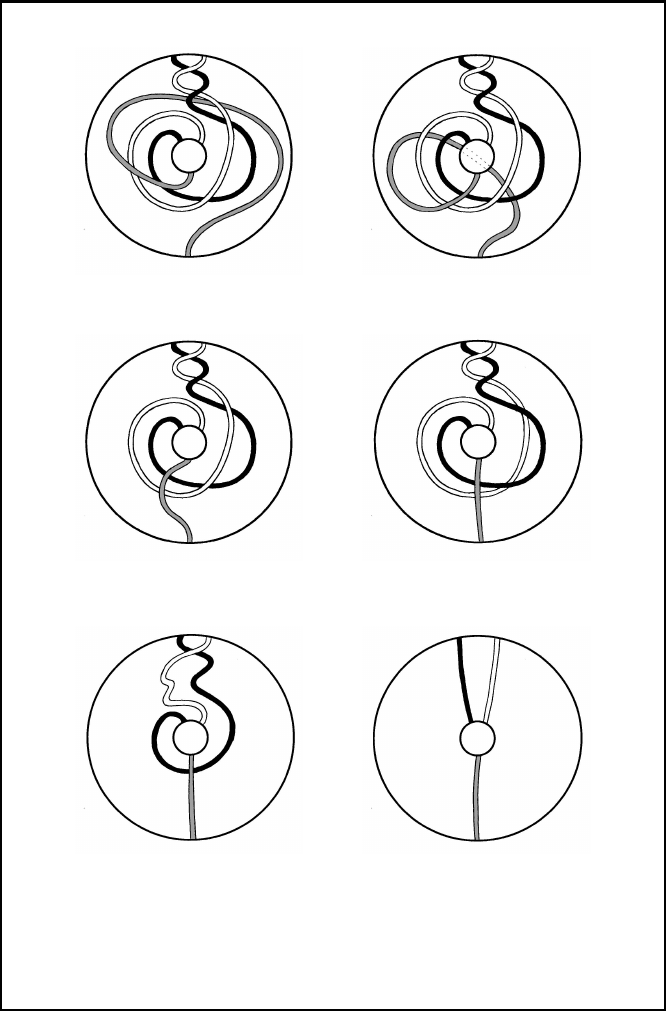
Exercises 507

Sidebar 7 (Cont.)

The gray string goes behind the rest...

... continues...

... and goe s back to its initial position.

The white string goes behind the black

string...

... and into position.

The black string is now free to take its

original place.

This magic trick (which may very well be done at home, using a pencil eraser, some tacks and

a yard or so of ordinary string) is a consequence of the double connectedness of SO( 3).

Another illustration of this fact is “Feynmann’s hand trick” [36].

Chapter

Introduction to probab ility

theory

Statistics is that science which proves

that 99.99% o f human beings have

more legs than the average number.

The goal of probability theory is to provide mathematical tools to discuss rigorously

the elusive c oncept of randomness.

Randomness means in general that we have incomplete knowledge of some system.

Probability theory is interested, for instance, in what can be said of an event when

an “experiment” is repeated a large number of times. For instance, this “experiment”

may be the throwing of a die, and the event might be “the result of the throw is at

most 3.”

However, probability the o ry is not only concerned with “random” events, since it

is also at the heart of the formalism of statistical mechanics, which, at the classical

level, is based on deterministic equations (the Newton equations, in the Lagrangian

or Hamiltonian formalism). It can also be used to describe in a simpler (maybe

incomplete) manner some very complicated distributions, such as in signal theory

or in image processing.

Finally, it should be mentioned that probability theory may be used to discuss vari-

ous events, and — as the case may be — to mislead, bluff, or h oodwink the unsuspecting

public. Although this is not something that students should do, it is important

that they know some of those techniques, not only to be capable of clear scientiﬁc

judgment (some experimental results are presented as “proved,”

whereas rig orous

statistical analysis shows them to be no better than purely random), but also to

enlighten the daily life o f an informed citizen.

510 Introduction to probability theory

19.1

Introduction

Dice are the embodiment of randomness. The Latin name, alea, is indeed

the source of the French word “aléatoire” for “random.” The Arabic word

az-zahr, which also means “dice,” has produced Spanish azar, French “hasard”

(“randomness”), as well as English “hazard.” The way dice fall, through the

Latin cadere (to fall), has brought the Old French word chaance and then th e

word “chance.”

According to a dictionary, chance is “The unknown and unpredictable element

in h appenings that seems to have no assignable cause.”

This is what happens w ith t he throw of a d ie. Even if we hold tha t t he

laws that dictate the fall and rebounds of the die are perfectly deterministic,

it is a fact that this system is chaotic and thus, in practice, has unpredictable

behavior: the ﬁnal outcome of the throw has no apparent reason [86].

It is quite remarkable that such a common concept as “chance” should at

the same time be so difﬁcult to fathom. Here is a math ematical example:

Some real numbers have the following property,

which we call Property P :











the decimal expansion of x contains statistically as many ze-

ros as ones, twos, threes, etc; morevoer, any ﬁnite sequence of

digits (for instance, “123456789” or your birthd ate) appears

in the decimal e xpansion and indeed appears statistically as

frequently as any other sequence of the same length (thus

“12345” is as f requent as “94281”).

Mathematicians (in particular, É. Borel) have proved that Propert y P holds

for the overwhelming majority of real numbers. More precisely, the probability

that P holds for a real number x is equal to 1. The probability that P does

not hold is therefore equal to 0.

Now, can you give me a single example of a real number such that Property P

holds?

It should be noted that rational numbers do not have Property P . Indeed,

the decimal ex pansion of a rational number is periodic (for example, 1/7 =

0.142857142857... with an inﬁnite repetition of the s equence “142857”), which

clearly contradicts Property P . Maybe a number such as π, or e, or

2 would

work. This is quite possible, but this is a complete mystery at the current

time: nobody has been able to show, for instance, that π h as Property P , nor

indeed that it doesn’t .

So, we know that a “randomly chosen” real number must almost surely

satisfy Property P ; yet, (almost) a ny time we chose a number, either it does

E.g., the famous case of “water memory,” which is described in detail in [15].

A number for which Property P holds is called a normal number.

Introduction 511

not have this property, or if it does, we are not able to prove it.

The conclusion

is that it is in fact very difﬁcult to make a “ random” choice of a real number;

most of our “choices” are not random at all.

This simple example should be enough to suggest how difﬁcult it may be to

express rigorously what is a “random choice.” To overcome those dif ﬁculties,

it has been necessary to formalize and axiomatize probability theory, leaving

aside questions of interpretation to concentrate solely on the mathematical

content.

In this sense, the forefathers of probability are certainly Blaise Pascal (see

page 606) and Pierre de Fermat (1601—1665), during a famous exchange of let-

ters during the summer 1654. The physicist Christiaan Huyghens (1629—1695)

published this correspondance in the ﬁrst treatise of probability theory, De Ra-

tiociniis in ludo aleæ, where in particular the notion of mathematical expecta tion

is introduced.

However, the works of Jacques Bernoulli (see page 555) and Abraham de

Moivre,

with the ﬁrst theorems concerning laws of large numbers, are the

real star ting point of modern probab ility theory. Laplace and Gauss studied

the theory of errors (with important applications to measurements such as

that of the terrestrial meridian).

In th e ninetheenth century, Pafnouti Tchebychev

(1821—1894) and his

students Andrei Markov (1856—1922) and Alexandre Liapounov (1857—1918)

created a formalism suitable for the study of sums of random variables,

which marks t he beginning of the important Russian school of probability

theory. The complete axiomatization of probability is due to Andrei Kol-

mogorov (see below), building on previous work of Sergei Bernstein (1880—

1968), Richard von Mises (1883—1953) and Émile Borel (1871—1956).

To be precise, we know a few normal numbers. For instance, the number obtained by ﬁrst

writing successively all positive integers, the n concatenating the resulting sequences of digits

(Champernowne, 1933):

0, 1234567891011121314151617 . . .

or the number obtained by doing t h e same with the sequence of prime numbers (Erdös and

Copeland, 1945) :

0, 23571113171923293137. . .

It is quite obvious that those numbers are artiﬁcial; in particular, they depend on the fact

that we work in base 10. So one may increase the difﬁculty by asking for an absolutely normal

number, one which is normal (in an obvious sense) in any basis. It seems that today not a

single absolutely normal number is known, whereas, again, “almost all” numbers must have this

property.

Consider also the great difﬁculty inherent in the wri ting of a random number generator

for a computer.

Abraham de Moivre (1667—1754) left France at eighteen during the repression against

Protestants. He discovered mathematics through a chance encounter with Newton’s Prin-

cipia [69]. Besides studies of complex numbers, he gave the mathemati cal deﬁnition of in-

dependent events, and proved the “Stirling” formula.

The mathematical great-great-great-great-grandfather of the translator.

512 Introduction to probability theory

19.2

Basic deﬁnitions

In this section, we introduce the b asic vocabulary of probability theory

and the axioms stated by Kolmogorov [19] in Über die analytischen Metho-

den in der Wahrscheinlichkeitrechnung (Analytic Methods of Probability Theory,

1931), and also in the historical book Grundbegriffe der Wahrscheinlichkeitrechnung

(Foundations of Probability Theory, 1933).

The probability of an event that can range only over a discrete set (such as

the result of throwing a die) can b e captured very intuitively. However, when

the space of possible events is continuous (such as the points in space, or an

instant in time), a precise mathematical description of the “probability that

an event occurs” is required.

Kolmogorov suggested that the probability of an event be the expression

of the measure of a set.

DEFINITION 19.1 A probability space is a pair (Ω, Σ), where

• Ω: a set (the sample space).

• Σ: σ-algebra of events, that is, a set such that

i) Σ ⊂ P(Ω) (P(Ω) is the set of a ll subsets of Ω);

ii) Ω ∈ Σ and ∅ ∈ Σ;

iii) if A ∈ Σ, then its complement ∁

Ω

A also belongs to Σ;

iv) if A

∈ Σ for any n ∈ N, then

n∈N

∈ Σ.

An element of Σ is called an event. An element of ω ∈ Ω is sometimes called

the result of the experiment Ω, or an atomic or elementary event.

The reader should recognize Deﬁnitions 2.7 and 2.10 on page 59. So a

measurable space is a probabilistic space.

Example 19.2 When playing (once) heads or t ails, one can take Ω = {P , F } and

Σ =



∅, {P }, {F }, {P , F }



Example 19.3 When rolling once a die with six facets, the space of elementary events can be

Ω = {1, 2, 3 , 4 , 5 , 6} and Σ = P(Ω).

The event “the result of the throw is even” is the element {2, 4, 6} ∈ Σ.

Example 19.4 Take Ω = R. Then both {∅, R} and



∅, [0, 1] , ∁

[0, 1] , R



are σ-algebras.

Remark 19.5 Note that it is sometimes useful to take for Ω a “set” which is not an abstract

mathematical object, but rath er a group of persons, a collection of objects, etc.

Basic deﬁnitions 513

DEFINITION 19.6 An event A ∈ Σ is realized if the result ω of an experi-

ment is in A.

Working with the σ-algebra Σ, we have at our dis posal on the set of

events the usual set-theoretic operations of union, intersection, and taking the

complementary subset. These have the following intuitive meaning:

• the union of two events A and B, that is, A ∪ B, corresponds to the

realization of A or B (an inclusive “or,” where A and B is possible);

• the intersection of two events A and B, i.e., A ∩ B, corresponds to the

realization of A and B;

• taking the complementary subset corresponds to the realization of the

opposite of A, or equivalently to the no-realization (the failure) of A.

DEFINITION 19.7 Let (Ω, Σ) be a sample probability space A, B ∈ Σ. Two

events A and B are simultaneously realized if the outcome of the experiment

is ω ∈ A ∩ B.

The events A and B are incompatible if A ∩ B = ∅.

A complete class of events is any countable (or ﬁnite) sequence of non-

empty events (A

)

n∈N

, which are mutually incompatible and which together

exhaust Ω, that is, such t hat

i) A

∩ A

= ∅ if m 6= n,

ii)

n∈N

= Ω.

Any element ary event {ω} ∈ P(Ω) is th en contained in one and only one of

the elements of the complete class.

DEFINITION 19.8 Let C ⊂ P(Ω) be any set of subsets of Ω. The intersection

of all σ-algebras containing C is a σ-algebra, which is called the σ-algebra

generated by CC

CC and is denoted σ(CC

CC ).

Example 19.9 Consider the experiment of rolling a die once. We take

Ω = {1, 2, 3 , 4 , 5 , 6} and we put Σ = P(Ω).

Consider now C =



{1, 2}



. The σ-algebra generated by C is

σ(C ) =



∅, {1, 2}, {3, 4, 5, 6}, Ω



On the other hand, if we put C =



{1}, {2}



, we have

σ(C ) =



∅, {1}, {2}, {1, 2}, {3, 4, 5, 6}, {1, 3, 4, 5, 6}, {2, 3, 4, 5, 6}, Ω



Having deﬁned these notions, which are basically set-theoretic in nature,

we can use the σ-algebra for th e purpose of deﬁning measures of sets in this

σ-algebra, as in the deﬁnition of the Lebesgue integral. A suitably normalized

positive measure will provide the notion of probability.

514 Introduction to probability theory

DEFINITION 19.10 (Probability measure) Let (Ω, Σ) denote a sample space

with a σ-algebra. A map P : Σ → R

is a probability (measure) on (Ω, Σ) if :

(P1) P(Ω) = 1;

(P2) for any countable (or ﬁnite) sequence (A

)

n∈N

of pairwise disjoint

events in Σ, we have



n∈N



n∈N

P(A

The triplet (Ω, Σ, P) is also called a probability s pace .

Comparing with Deﬁnition 2.11 on page 59, we see that a probab ility space

is simply a measure space where the total measure of the space is supposed to

be equal to 1.

The reader is then invited to check the following propert ies:

PROPOSITION 19.11 Let P be a probability measure. Then the following properties

hold:

i) if A ⊂ B, then we have P(A) ¶ P(B);

ii) P



∁

Ω



= 1 −P(A);

iii) if A ⊂ B, then we have P(B) = P(A) + P(B \ A);

iv) P(A ∪ B) = P(A) + P(B) −P(A ∩ B);

v) if (A

)

n∈N

is an increasing sequence (for inclusion), then we have



n∈N



= sup

n∈N

P(A

) = lim

n→∞

P(A

);

vi) if (A

)

n∈N

is a decreasing sequence (for inclusion), then we have



n∈N



= inf

n∈N

P(A

) = lim

n→∞

P(A

Example 19.12 Let a ∈ Ω be an elementary e vent. The map

: P(Ω) −→{0, 1},

A 7−→

1 if a ∈ A,

0 if a /∈ A

is a probability measure, which is called the Dirac measure or mass at a.

Example 19.13 Let (p

)

n∈N

be an arbitrary sequence of non-negative real numbers such that

n∈N

= 1. Let Ω be any set and let (x

)

n∈N

be a sequence of e l ements in Ω. Then

n∈N

deﬁnes (in an obvious way) a probability measure on



Ω, P(Ω)



Basic deﬁnitions 515

Andrei Nikolaievitch Kolmogorov (1903—1987) could not receive any

education from his parents, as his mother died in childbirth and his

father, an agriculturist, was in exile. He was raised by his aunt and

became a train conductor. In his free time, Kolmogorov wrote a

treatise on Newtonian mechanics. His further works dealt with very

varied subjects: trigonometric series, the axiomatization of probabil-

ity theory, the theory of Markov processes, information theory. In

physics, his contributions were important in the theory of turbu-

lence, the study of chaotic systems and dynamical systems (his initial

remains in the acronym “K AM theory,” with Arnold’s and Moser’s).

He also had deep interests outside mathematics, including the poeti c

works of Pushkin.

Example 19.14 Let f : R

→ R

be an integrable function (with respect to Lebesgu e measure)

such that

f dµ = 1. For any Borel subset A ∈ B(R

) (recall that the Borel σ-algebra is the

σ-algebra on R

generated by op en sets, or equivalently by “rectangles” [a

, b

] ×···×[a

, b

]),

let

P(A) =

f dµ.

The map P thus deﬁned i s a probability measure on



, B(R

)



Example 19.15 Let σ be a positive real number, and let m ∈ R. The Gauss distribution or

normal distribution with mean m and standard deviation σ is the probability measure on R

(with respect to the Borel σ-algebra) deﬁned by

P(A) =

2π

exp



(t −m)

2σ



dt for any A ∈ B(R).

DEFINITION 19.16 A subset N ⊂ Ω is negligible (for a given probability

measure P) if it is contained in a measurable subset (and event) with probabil-

ity zero:

∃N

′

∈ Σ N ⊂ N

′

and P(N

′

) = 0.

A property p that depends on elementary events h olds almost surely or

is almost s ure if the set of those ω which do not satisfy p, namely, the set



ω ∈ Ω ; p(ω) is false



is negligible.

Example 19.17 Let Ω = [0, 1], with the Borel σ-algebra Σ = B



[0, 1]



and the “uniform”

probability measure on [0, 1] (i.e., the Lebesgue measure restricted to [0, 1]). Then for x ∈ [0, 1],

x is almost surely an irrational number.

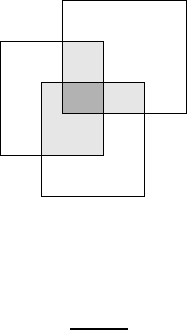
516 Introduction to probability theo ry

Fig. 19.1 — The Poincaré formula for n = 3. In dark gray, A ∩B ∩C ; in light gray, A ∩B,

A ∩ C and B ∩ C .

19.3

Poincar

e formula

Consider two events A and B. Obviously (just using the deﬁnition as the

measure of the corresponding e vents) we have the formula

P(A ∪ B) = P(A) + P(B) −P(A ∩ B).

Can this be generalized to more than two events? Let A, B, C be three

events. We can compute

P(A) + P(B) + P(C ) −P(A ∩ B) −P(B ∩ C ) −P(C ∩ A),

but as clearly seen in Figure 19.1, this is not th e correct result for P(A ∪B ∪C ),

because the subset A ∩ B ∩ C has been counted three times, then subtracted

three times. Hence the correct relation is in fact

P(A ∪ B ∪ C ) = P(A) + P(B) + P(C ) −P(A ∩ B)

−P(B ∩ C ) −P(C ∩ A) + P(A ∩ B ∩ C ).

With this done, the general result is easy to guess and prove.

THEOREM 19.18 (Poincar

e formula) Let n ∈ N

∗

and let A

, . . . , A

be arbitrary

events, not necessar ily disjoint. Then we have



i=1



k=1

(−1)

k+1

1¶i

<···<i

¶n

P(A

∩···∩ A

Proof. A proof using random variables, as deﬁned in the next chapter, is given in

the Appendix D. A n element ary proof by induction is also easy.