Антонов В.Ф. Практикум по биофизике

Подождите немного. Документ загружается.

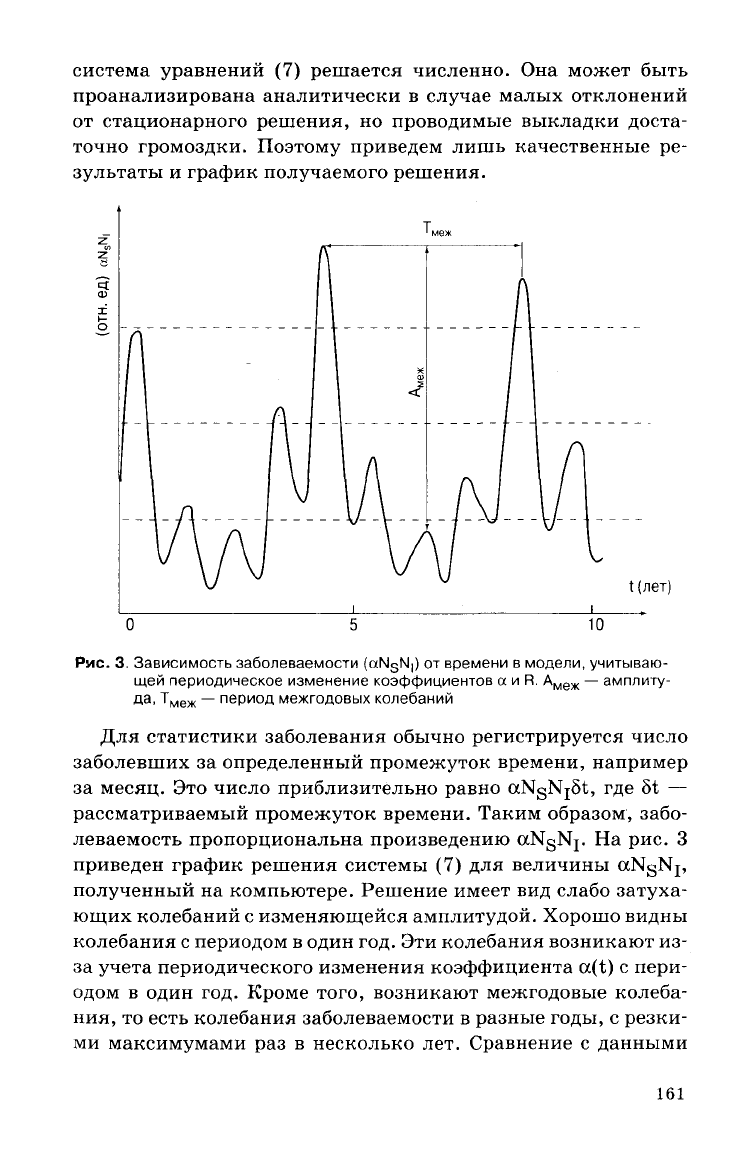
система уравнений (7) решается численно. Она может быть

проанализирована аналитически в

случае

малых отклонений

от стационарного решения, но проводимые выкладки

доста-

точно громоздки. Поэтому приведем лишь качественные ре-

зультаты

и график получаемого решения.

(лет)

Рис.

Зависимость

заболеваемости (aN

N|) от времени в

модели,

учитываю-

щей

периодическое

изменение

коэффициентов а и R.

меж

— амплиту-

да,

меж

—

период

межгодовых колебаний

Для статистики заболевания обычно регистрируется число

заболевших за определенный промежуток времени, например

за месяц. Это число приблизительно равно aNgNj5t, где 8t —

рассматриваемый промежуток времени. Таким образом, забо-

леваемость пропорциональна произведению aNgNj. На рис. 3

приведен график решения системы (7) для величины aNgNj,

полученный на компьютере. Решение имеет вид слабо

затуха-

ющих колебаний с изменяющейся амплитудой. Хорошо видны

колебания с периодом в один год. Эти колебания возникают из-

за

учета

периодического изменения коэффициента a(t) с пери-

одом в один год. Кроме того, возникают межгодовые колеба-

ния,

то есть колебания заболеваемости в разные годы, с резки-

ми

максимумами раз в несколько лет. Сравнение с данными

161

реальной заболеваемости коклюшем (см. рис. 1) показывает,

что данная модель, по крайней мере качественно, хорошо опи-

сывает реальный эпидемический процесс. Эта модель является

адекватной.

Пользуясь моделью, можно проследить влияние различных

параметров заболеваний, в частности амплитуды

годовых

ко-

лебаний коэффициента a(t) и времени запаздывания At, на ха-

рактер получаемого решения. Это удобно делать с помощью

компьютера, вводя различные значения параметров модели.

Оказывается, что при невыраженной сезонности заболевания

(маленькая

амплитуда колебаний a(t)) многолетняя циклич-

ность (увеличение заболеваемости через несколько лет) незна-

чительна, а при выраженной сезонности цикличность велика.

На

многолетнюю цикличность также сильно влияет величина

времени запаздывания.

Выполнение работы

1. Простейшая

модель

постоянными

коэффициентами.

На

компьютере рассчитывается простейшая модель эпиде-

мического процесса, описываемая системой уравнений:

dNj/dt

= aNgNj - PNj,

/dt

= y(N - N

) - О.ЩЩ, (1)

где Nj — число инфицированных членов популяции, Ng —

число восприимчивых членов, t — время,

a = R/(NT) (2)

—

постоянный коэффициент, характеризующий заражение,

R — среднее число лиц, к которым передается возбудитель от

одного инфицированного человека за все время болезни, т —

средняя

продолжительность заболевания,

Р=1Л

—

коэффициент выздоровления,

у=1/Т

—

коэффициент смерти, где Т — средняя продолжительность

жизни.

162

Решение

системы (1) для малых отклонений w(t) от стацио-

нарного

решения имеет вид

затухающих

колебаний:

w(t) = A

з cos(oot + ф^, (3)

где

= 2/( yR), (4)

— время затухания, ,

со

« Vp>(R-l) (5)

— круговая частота.

Задание

1. Ввести некоторые значения параметров:

коэффи-

циента

R (например, R = 4 или

другое

значение), длительности

заболевания в днях (от 5 до 40), начальную долю восприимчи-

вых Ng/N вблизи значения 1/R в процентах (от 1/R + 0,1% до

1/R +

3,0%).

Например, при R = 4 1/R = 25%, 1/R + 0,5% =

25,5% . Нажать клавишу Enter. На экране появляется график

зависимости заболеваемости (в относительных единицах) от

времени.

Зарисовать график в тетрадь. Ввести

другую

дли-

тельность заболевания при том же начальном уровне воспри-

имчивых. Построить и зарисовать полученный график. Срав-

нить

полученные графики с экспериментальной зависимостью

заболеваемости коклюшем от времени (рис. 1). Сделать вывод

об адекватности простейшей модели.

Задание

2. Пользуясь формулами (3) — (5), рассчитать для

некоторых значений параметров характерное время затухания

период колебаний. Сравнить с периодом колебаний экспери-

ментальной зависимости.

2. Модель с

запаздыванием

периодически

меняющейся

вероятностью

передачи

инфекции.

Эта модель описывается системой дифференциальных урав-

нений:

dNj(t)/dt

a(t)N

(t)N

- At) - (3N

(t) (6)

(t)/dt

= 7(N -

(t))

a(t)N

(t)N

- At), (7)

где At — характерное время от заражения до заражения,

a(t)

= a

4- Asin(co

t + ф),

163

— постоянная составляющая, щ = 2л/Т

, Т^ — период в

один

год. Параметр R связан с а соотношением (2).

На

компьютере рассчитывается решение системы (7) с за-

данными

параметрами. На экран выводится зависимость забо-

леваемости (в относительных единицах) от времени, а также

периодически изменяющийся коэффициент R.

Задание

3. Ввести значения параметров: амплитуду измене-

ния

коэффициента R в процентах (от 0 до 3,0), время запазды-

вания

в днях (от 2 до 20). Нажать клавишу Enter. На экране

появляется

зависимость заболеваемости от времени (белым

цветом),

рассчитанная в течение одного

года,

и R(t) (зеленым

цветом).

Для продолжения расчета нажать

любую

клавишу.

Подбирая

параметры, получить зависимость заболеваемости

от времени, рассчитанную в течение нескольких лет, с четко

выраженными межгодовыми колебаниями. Зарисовать гра-

фик

в тетрадь. Сравнить полученный график с эксперимен-

тальной зависимостью заболеваемости коклюшем от времени

(рис.

1). Сделать вывод об адекватности рассматриваемой мо-

дели.

Задание

4. Ввести последовательно несколько значений вре-

мени

запаздывания в днях (от 2 до 20) при фиксированной ве-

личине

амплитуды колебаний коэффициента R(t) (например

1,5 или

другое

значение). Как влияет изменение времени запаз-

дывания

на амплитуду межгодовых колебаний заболеваемости

на их период? Амплитудой межгодовых колебаний назовем

максимальную разность (по всем годам)

между

максимальны-

ми

значениями заболеваемости в течение одного

года

(локаль-

ными

максимумами), см. рис. 3. Периодом межгодовых коле-

баний

назовем время

между

локальными максимумами в годы

с пиками заболеваемости. Результаты записать таблицу:

Время

запаздывания

Амплитуда

межгодовых

колебаний

Период

межгодовых

колебаний

Сделать и записать качественный вывод.

164

Задание

5. При фиксированном времени запаздывания (на-

пример, 4 дня или

другое

значение) ввести несколько значе-

ний

амплитуды колебаний коэффициента R(t) (от 0 до 3). Как

влияет изменение амплитуды колебаний R(t) на амплитуду и

период межгодовых колебаний aN

Nj? Результаты записать в

таблицу:

Амплитуда

коэффициента

Амплитуда

межгодовых

колебаний

Период

межгодовых

колебаний

Сделать и записать качественный вывод.

Приложение.

Рассмотрим решение системы уравнений (1) в

случае

малых отклонений от стационарного решения. Поло-

жим Ng(t) = NgQ + v(t), Nj(t) = NjQ + w(t). После подстановки в

систему (1) получим:

dw/dt

= y(R ~ l)v + avw,

dv/dt

= -yRv - pw - avw.

(П1)

Для малых отклонений v и w член avw мал по сравнению с

другими членами системы (П1), и им можно пренебречь. В ре-

зультате

получаем систему:

dw/dt

dv/dt

= -yRv - Pw. (П2)

Эта система дифференциальных уравнений может быть

сведена к одному дифференциальному уравнению второго по-

рядка. Действительно, продифференцируем второе уравне-

ние

(П2):

v/dt

-yRdv/dt

- pdw/dt.

Исключая

dw/dt

с помощью первого уравнения (П2), получаем

дифференциальное уравнение второго порядка с постоянными

коэффициентами:

v/dt

yRdv/dt

+ py(R - l)v = 0. (ПЗ)

165

Его решение ищем в виде:

v(t) =

После

подстановки в (ПЗ) находим характеристическое

уравнение для к:

+ yRk + (3T(R -1) = 0.

Решения

этого квадратного уравнения имеют вид:

1>2

= (-yR ±

V5)/2.

где дискриминант

= (

- 4py(R - 1).

Можно

показать, что при реальных значениях параметров

дискриминант

D < 0, a kj и к

— комплексные. В математике

показывается, что в этом

случае

дифференциальное уравнение

(ПЗ)

описывает затухающие колебания, а его решение имеет

вид:

v(t) = А

Тз

cos(cot + ф

где

= 2/(yR), со = A/(3Y(R - 1)- (yR)

/4.

Вспомним,

что Р = 1/т, у= 1/Т, где х — средняя продолжитель-

ность заболевания, Т — средняя продолжительность жизни. Сле-

довательно, Р > Y(a часто Р »у). Если при этом R - 1

1, то

со

Vpy(R

—1).

Из

второго уравнения (П2) можно найти

w(t) = A

cos(cot

Покажем

теперь, при каких значениях параметров D < 0.

Неравенство D < 0 можно переписать в виде

< 4pY(R-l),

откуда

у/р < 4(R-1)/R

или

х/Т < 4(R — 1)/R

. (П4)

166

Если R-l 3= 1, то это условие выполняется при реальных

значениях R, так как т < Т. При R близких к 1 можно пока-

зать, что (П4) выполняется при

+T/2T.

Таким

образом, практически

всегда

дискриминант D харак-

теристического уравнения для к отрицателен, то есть уравне-

ние

(ПЗ) и система (П2) описывают

затухающие

колебания.

Характерное время затухания порядка средней продолжи-

тельности жизни.

4.5.

Фармакокинетическая

модель

Фармакокинетическая

модель описывает кинетику (изме-

нение

во времени) распределения введенных в организм пре-

паратов (лекарств, индикаторов). Терапевтический эффект

препарата зависит от его концентрации в больном органе (ор-

гане-мишени) и времени нахождения в органе при оптималь-

ной

концентрации лекарства.

Задачей врача является выбор дозы, способа и периодично-

сти введения лекарства, обеспечивающих максимальный тера-

певтический эффект при минимальных побочных явлениях.

Цель создания фармакокинетической модели — помочь в ре-

шении

этой задачи.

Фармакокинетическая

модель позволяет в пределах опреде-

ленных допущений найти изменения концентрации препарата

во времени при различных способах его введения в организм,

рассчитать оптимальное соотношение

между

параметрами

ввода и вывода препарата для обеспечения необходимого тера-

певтического эффекта.

Цель

работы:

Познакомиться

с задачей моделирования кинетики лекар-

ственных препаратов в организме. Научиться составлять про-

стейшие кинетические уравнения, описывающие фармакоки-

нетическую модель и анализировать их решение.

167

Литература:

Х.Антонов

В.Ф.

и др.

Биофизика.

— М.:

Владос,

2000.

Владимиров ЮЛ. и др.

Биофизика.

— М.:

Медицина,

1983.

Данное

методическое

пособие.

Подготовка

работе

Изучить по рекомендованной

литературе

следующие

во-

просы:

1. Фармакокинетическая модель (общая

схема,

метод

со-

ставления уравнений).

2. Упрощенная

схема

модели. Составление дифференциаль-

ных уравнений, описывающих изменение во времени концен-

трации лекарства в крови.

3. Анализ решений при разных способах введения лекар-

ства.

Теоретические

сведения

При

составлении дифференциальных уравнений, описы-

вающих кинетику распределения лекарств, используются

следующие, известные из физиологии, факты. Концентрация

препарата в крови зависит: 1) от всасывания препарата в кро-

веносное

русло

(константа всасывания kj) при внесосудистом

введении; 2) от транспорта лекарства из крови в орган-ми-

шень и обратно (константы к

з и к

2); 3) от удаления препа-

рата из крови и разрушения, инактивации препарата (кон-

станта к

Соответствующая

схема

показана на рис. 1.

Кожа,

мышцы

кишечник

Кровь

Орган-

мишень

Рис.

1. Схема

кинетики

распределения

лекарства

Каждый процесс, изображенный стрелкой, можно предста-

вить в виде химической реакции первого порядка (скорость реак-

ции

пропорциональна концентрации реагирующего вещества)

168

dCi

—

= -k

——

= k^ -

(1)

где

, C

—

концентрации

соответствующем блоке моде-

ли

(рис.

1).

Уравнения

(1)

выражают баланс массы лекарственного

ве-

щества

соответствующем блоке модели. Производные,, стоя-

щие

уравнении, имеют смысл изменения концентрации

за

единицу времени.

Их

величина естественно определяется

вве-

денной

выведенной массой вещества

за это

время.

Решение

этих уравнений

дает

зависимость концентрации

(t).

Система уравнений

(1) —

система дифференциальных

уравнений первого порядка, аналитическое решение которой

затруднительно, решить систему можно

применением специ-

альных методов

ПК.

Упрощенная

модель.

Рассмотрим более простую модель,

которой

предусмотрим возможность введения препарата непо-

средственно

кровь

(в

виде непрерывного введения

со

скоро-

стью

Q или

разового введения

виде разовой (нагрузочной)

до-

зы

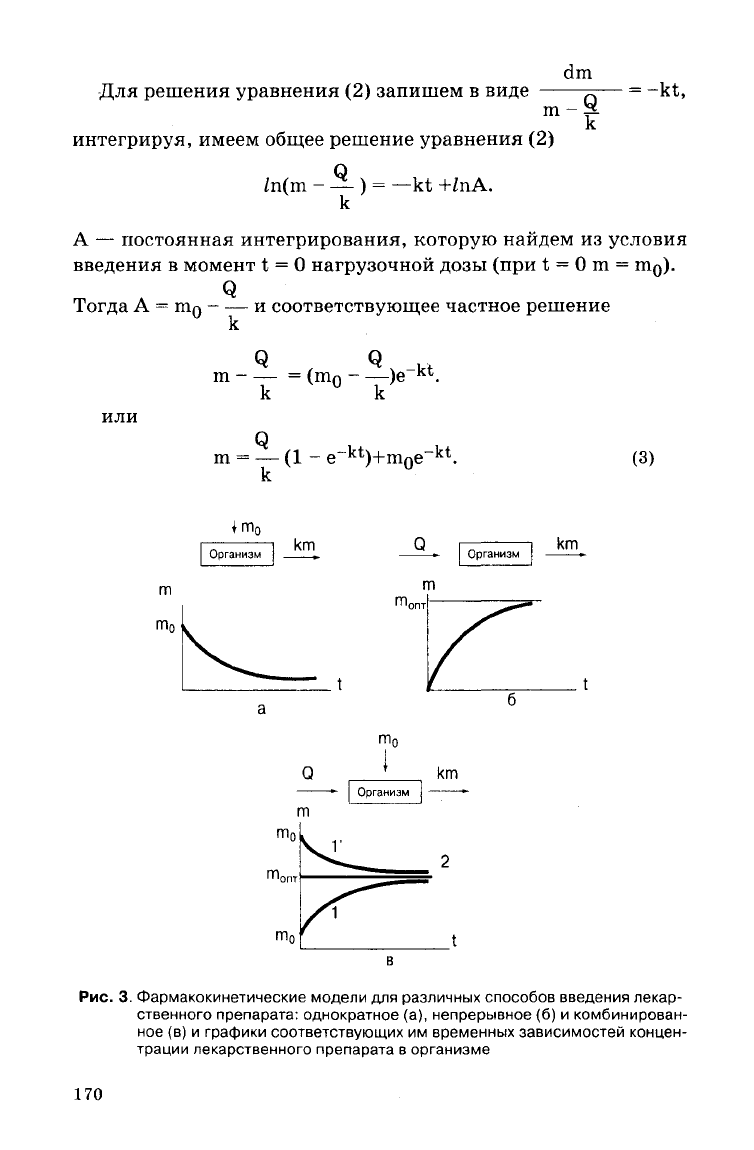
Схема модели показана

на

рис.

кровь

m(t)

— ?

Рис.

Схема модели

(к —

константа выведения препарата

из

крови)

Дифференциальное

уравнение (кинетическое уравнение)

для m(t) запишется

виде:

Q-km (2)

где

m —

масса препарата

крови,

—

скорость изменения

массы препарата.

169

Для решения уравнения (2) запишем в

виде

•

= -kt,

интегрируя, имеем общее решение уравнения (2)

/п(ш - — ) = —kt +ZnA.

А — постоянная интегрирования,

которую

найдем из условия

введения в момент t = 0 нагрузочной дозы (при t = 0 m = nig).

Тогда

А = m

- — и

соответствующее

частное решение

или

4 kt

m — — = (nig - —)e

кь

m = — (1 - e""

)+m

(3)

Организм

Рис. З. Фармакокинетические модели для различных способов введения лекар-

ственного

препарата: однократное (а), непрерывное (б) и комбинирован-

ное (в) и графики соответствующих им временных зависимостей концен-

трации лекарственного препарата в организме

170