Антонов В.Ф. Практикум по биофизике

Подождите немного. Документ загружается.

ми,

а форма фазовой траектории становится отличной от эл-

липсоидальной .

4. Проведите исследование с помощью ПК, при каких соот-

ношениях параметров модель "хищник—

жертва"

практичес-

ки

превращается в модель естественного роста.

Варианты изменения параметров приведены в таблице:

Параметры

1 система

2 система

3 система

система

е,

1/год

0,5

Р.

1/год

0,72

0,0125

0,009

ст

Уст

Начальные

условия

= х

ст

+дх

= х

ст

0,О5х

ст

= х

ст

+0,1х

ст

= х

ст

+О,5х

ст

+х

ст

У0

Уст

+А

У=Уст

Сопоставьте расчетные кривые изменения x(t) и y(t) с экспе-

риментальными кривыми, представленными на рис. 1.

4.4.

Математическое

моделирование

эпидемического

процесса

Математической

моделью

называют описание реального

процесса с помощью математических уравнений. Исследова-

ние

этих уравнений помогает понять поведение системы, а

главное, предсказать ход процессов при изменении условий. В

данной работе рассматривается математическое моделирова-

ние

на примере модели эпидемического процесса.

Эпидемический процесс — это цепь инфицирований и пере-

дач инфекционного заболевания от одного человека к

друго-

му. Более строго, эпидемическим процессом называют "само-

регулирующийся процесс взаимодействия гетерогенных из-

менчивых популяций возбудителя заболевания и хозяина".

Это сложное явление, включающее в себя не только биологи-

ческие, но и социальные компоненты. Математическое моде-

лирование помогает получить прогноз развития эпидемичес-

кого процесса и, следовательно, принять возможные меры по

снижению заболеваемости.

151

Цель

работы:

1. Изучить математическое моделирование на примере мо-

дели эпидемического процесса.

2. Исследовать влияние параметров модели на получаемое

решение.

Литература:

1. Данное пособие.

Анщонов

В.Ф. и др.

Биофизика.

— М.: Владос, 2000.

Подготовка

работе.

Изучить следующие вопросы:

1. Что такое моделирование? Математическое моделирова-

ние.

2. Адекватность и границы применимости модели.

3. Система уравнений простейшей модели эпидемического

процесса. График получаемого решения.

4. Система уравнений модели эпидемического процесса с

учетом

запаздывания и зависимости коэффициентов от време-

ни.

График получаемого решения.

Теоретические

сведения

При

построении математической модели эпидемического

процесса необходимо учитывать многие его особенности. Пере-

числим некоторые из них.

1. Для большинства инфекций заболевание оканчивается

выработкой иммунитета, предохраняющего хозяина от по-

вторного заражения. По этому признаку инфекции можно раз-

делить на следующие группы:

а) приводящие к выработке пожизненного иммунитета (на-

пример,

корь, дифтерия);

б) приводящие к выработке временного иммунитета (напри-

мер,

бактериальные дизентерии);

в) не приводящие к выработке иммунитета (например, си-

филис,

гонорея,

СПИД).

2. В различных фазах заболевания выделение возбудителя

во внешнюю

среду

неодинаково. Некоторое время после

инфи-

152

цирования,

когда инфекционный процесс только развивается,

возбудитель

не выделяется. В конечной фазе заболевания вы-

деление возбудителя обычно также менее интенсивно. Следо-

вательно, вероятность передачи инфекции от больного к здоро-

вым членам популяции зависит от времени, прошедшего с мо-

мента заражения. Кроме того, вероятность передачи инфек-

ции

часто зависит от времени

года.

3. Популяция хозяев неоднородна. В силу как биологичес-

ких, так и социальных особенностей вероятность инфицирова-

ния

разных членов популяции неодинакова.

4. Популяция возбудителя также неоднородна, в ней есть

более или менее вирулентные штаммы.

5. Вероятность смерти членов популяции зависит от их воз-

раста.

1970

1975

1980

1985

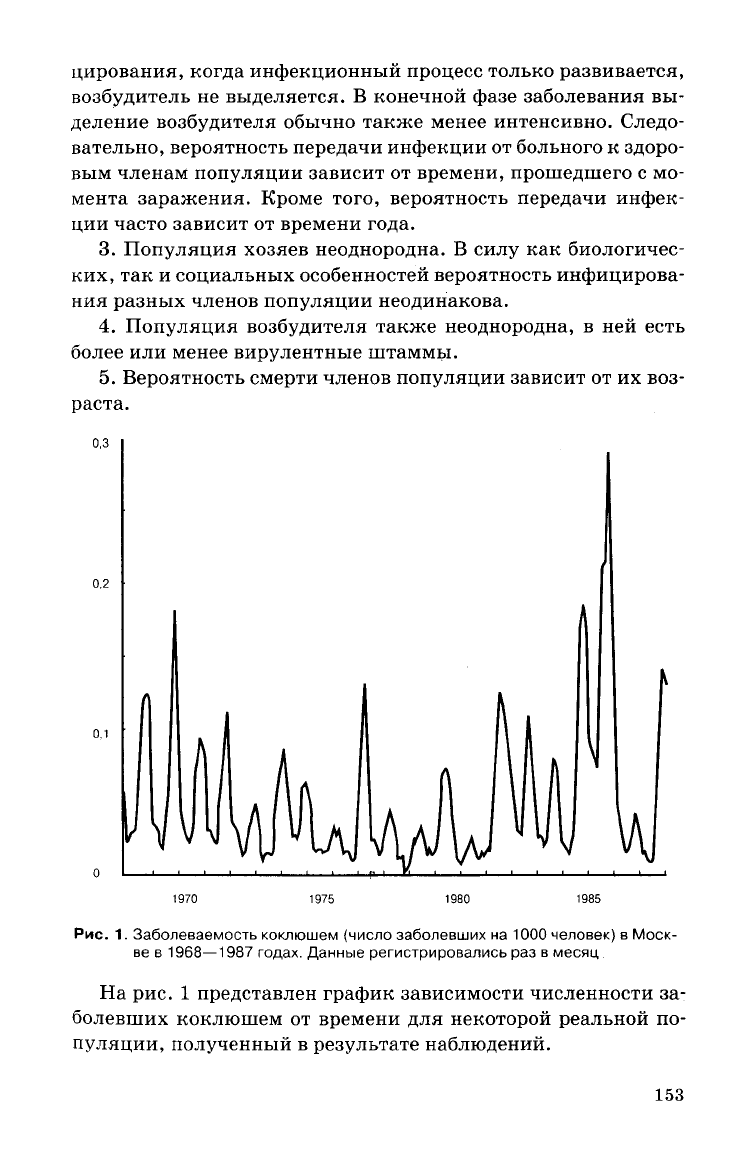
Рис.

1. Заболеваемость коклюшем (число заболевших на 1000 человек) в

Моск-

ве

в 1968—1987 годах. Данные

регистрировались

раз в

месяц

На

рис. 1 представлен график зависимости численности за-

болевших коклюшем от времени для некоторой реальной по-

пуляции,

полученный в

результате

наблюдений.

153

Для построения математической модели эпидемического

процесса сделаем следующие общие допущения:

1) рассмотрим инфекционные заболевания с пожизненным

иммунитетом;

будем

считать, что численность популяции людей не из-

меняется

с течением времени;

3) популяция возбудителя однородна.

Рассмотрим сначала простейшую модель с максимальным

количеством дополнительных упрощений, а затем усложним

ее,

стараясь приблизить к реальному процессу.

Простейшая

модель.

Дополнительно к сделанным выше

предположениям

будем

считать, что:

1) популяция людей однородна;

2) вероятность смерти человека не зависит от возраста;

3) вероятность выздоровления человека не зависит от вре-

мени,

прошедшего с момента заражения;

4) вероятность передачи инфекции не зависит от времени

года.

Для построения математической модели выделим три состо-

яния.

Это:

— восприимчивый, т.е. не болеющий и еще не болевший

этим

инфекционным заболеванием человек, который впослед-

ствии может заразиться;

— инфицированный человек;

— иммунный, т.е. имеющий иммунитет в

результате

пере-

несенного

заболевания человек.

Пусть N — численность рассматриваемой популяции, Nj —

число инфицированных, N

— число восприимчивых членов

популяции.

Введем коэффициенты, характеризующие следующие про-

цессы:

а — коэффицицент, характеризующий заражение воспри-

имчивых членов популяции;

р — коэффициент, характеризующий выздоровление

инфи-

цированных

членов;

у — коэффициент, характеризующий смерть членов попу-

ляции.

154

Запишем скорости

соответствующих

процессов:

а) Заражение восприимчивых членов популяции (переход

"восприимчивые" — "инфицированные"). Увеличение числа

инфицированных членов популяции за малый промежуток

времени dt пропорционально как имеющемуся числу

инфици-

рованных членов Nj, так и числу восприимчивых членов Ng,

т.е. приращение dNj равно:

Если все члены популяции восприимчивы, то за время dt

возбудитель

передается от одного инфицированного к aNdt

членам популяции. За все время болезни

возбудитель

пере-

дается от одного инфицированного в среднем к R членам,

причем

R = aNx

соответственно

a = R/(Nx),

где х — средняя длительность заболевания. Величина R

служит

числовой мерой заразности заболевания.Если R > 1, то есть за

время болезни один инфицированный заражает в среднем боль-

ше одного члена популяции, то инфекция вызывает массовые

заболевания. Если же R < 1, то заболеваемость уменьшается по-

сле заноса инфекции, и массовая эпидемия не возникает.

б) Выздоровление инфицированных людей. За малый про-

межуток времени dt выздоравливает число инфицированных,

равное

PNpdt.

Коэффициент

= 1/х,

где X — средняя продолжительность заболевания. Нетрудно

видеть, что

ос/Р

= (R/N х) х = R/N.

в) Смерть иммунных и инфицированных членов популя-

ции.

За малый промежуток времени dt по причинам,не связан-

ным

с данным заболеванием,

умирает

число людей, равное

yNdt. При этом

155

Y=l/T,

где Т — средняя продолжительность жизни. Поскольку чис-

ленность популяции постоянна, одновременно рождается такое

же количество новороженных, которые, однако, не имеют им-

мунитета. Так как число невосприимчивых (иммунных и ин-

фицированных) членов популяции равно N—Ng, то среди не-

восприимчивых членов умирает число, равное y(N-Ng)dt. Из-

менение числа восприимчивых членов Ng и невосприимчивых

(N-Ng)

результате

смерти и рождения можно представить в

виде таблицы:

Восприимчивые чле-

ны популяции,

Невосприимчивые чле-

ны популяции,

N—N

Смерть

-yN

-y(N-N

)

Рождение

+yNdt

Изменение

+y(N-N

)

-y(N-N

)

Таким

образом, в

результате

рождения и смерти прираще-

ние

числа восприимчивых членов популяции равно

7(N-N

)

dt.

В итоге общие скорости изменения числа инфицированных

членов популяции dNj/di? и числа восприимчивых членов

dNg/dt равны соответственно

dNj/dt = ocNgNj — PN

dNg/dt =

T(N

- N

) - aNgNj. (1)

Мы

получили систему дифференциальных уравнений, описы-

вающих динамику эпидемического процесса в простейшем слу-

чае. Общее решение этой системы может быть получено только

численными методами. Далее мы приведем некоторые аналити-

ческие результаты, позволяющие понять характер решения.

Найдем стационарное решение системы (1). Положив

dNj/dt = 0, dNg/dt = 0, полчим два решения.

Первое:

Nio

= О- N

= N

—

тривиальное решение, инфицированных членов популяции

нет.

Второе решение нетривиальное:

156

= T(R - 1) /a, N

= p/a = N/R.

При

R < 1 получаем единственное стационарное решение

NJO

= 0, Ngg = 0. Второе решение N

< 0, N

> N не имеет фи-

зического смысла.

Рассмотрим отклонения от ненулевого стационарного реше-

ния.

Положим N

(t) = N

Q + v(t), Nj(t) =

NJQ

+ w(t). Можно по-

казать (см. Приложение), что в

случае

малых отклонений v и

w система (1) сводится к следующей системе уравнений для

w(t) и v(t):

dw/dt

= 7(R - l)v,

dv/dt

= -yRv - p\v.

В Приложении показано, что ее решение имеет вид

_ t _ t

w(t) cos(cot

, v(t) = A

Тз

cos(cot + cp

), (3)

(Формула для со справедлива при т «Т, R ^ 2, где т — про-

должительность заболевания, Т — продолжительность жизни.)

Анализ результатов. На рис. 2 показаны графики полу-

ченного решения для относительного числа инфицирован-

ных I = Nj/N при

двух

значениях со. Это затухающие колеба-

ния

около стационарного решения, аналогичные

затухаю-

щим колебаниям пружинного маятника при наличии сопро-

тивления среды.

(лет)

Рис.

Зависимость

относительного числа инфицированных членов популяции

от

времени в

простейшей

модели

157

Частота этих колебаний — со, а характерное время

затуха-

ния

— т

. Малое отклонение от стационарного решения, воз-

никшее

в начальный момент времени,

будет

уменьшаться, со-

вершая при этом колебания около стационарного значения.

Характерное время затухания — это время, через которое амп-

литуда

колебаний уменьшается в е = 2,72 раз. Из формулы

видно,что

= 2/(

R) = 2T/R (4)

порядка

среднего времени-жизни человека Т при не слишком

больших R. (Напомним, что R численно равно среднему числу

лиц,

которым передается возбудитель от одного инфицирован-

ного человека за время болезни.)

Период

колебаний:

= 2 л/со « 2TIVXT/(R — 1) (5)

зависит от времени жизни, средней продолжительности забо-

левания

и от параметра R. На рис. 2 представлены два реше-

ния

для разных т. При реальных значениях параметров полу-

чаем периоды колебаний около

10—20

лет.

Анализ исходной системы уравнений (1) показывает, что не

только малые, но и большие отклонения уменьшаются со вре-

менем,

в отличие от модели "хищник — жертва", где решение

имеет характер незатухающих колебаний.

Сравним

полученные результаты с данными о реальной за-

болеваемости. График реальной заболеваемости коклюшем

приведен на рис. 1. Видно, что в отличие от полученного реше-

ния

реальная заболеваемость имеет характер незатухающих

колебаний.

Виден период этих колебаний в один год, который

сильно

отличается от полученного нами периода. Кроме того,

хорошо видны межгодовые колебания заболеваемости. В

неко-

торые годы заболеваемость резко возрастает, причем такое воз-

растание повторяется через несколько лет. Все эти особеннос-

ти не описываются простейшей моделью.

Таким

образом, простейшая модель не является адекватной

для описания заболеваемости коклюшем (и многими другими

заболеваниями).

Неадекватность модели является следствием

сделанных допущений. Будем теперь усложнять модель, отка-

зываясь от упрощающих предположений.

158

II.

Модель с

учетом

изменения

заразности

инфицирован-

ных.

Снимем предположение

(4) в

простейшей модели

посто-

янной

вероятности передачи инфекции

при

встрече инфициро-

ванного

восприимчивого членов популяции. Действительно,

для инфекционных заболеваний количество возбудителя

в ор-

ганизме хозяина

интенсивность

его

выделения

окружаю-

щую

среду

разные периоды заболевания неодинаковы. Сразу

после заражения возбудителя мало

и его

выделение практиче-

ски

не

происходит.

По

мере размножения возбудителя

его ко-

личество

заразность возрастают,

а в

заключительной фазе

за-

болевания

—

уменьшаются. При этом динамика заразности

во

время заболевания может быть весьма сложной.

Так,

напри-

мер,

при

инфекции СПИД

первые недели после заражения

крови инфицированного имеется небольшое количество виру-

сов, затем после выработки иммунного ответа

его

количество

резко уменьшается

вновь возрастает

уже

через несколько

лет

в фазе клинических проявлений СПИДа. Кроме того, инфек-

ции

активизируют механизмы, увеличивающие выделение

возбудителя

во

внешнюю

среду

(такие,

как

кашель

насморк

при

гриппе

понос

при

дизентерии

холере).

тому

же ряд

возбудителей находится

во

внешней среде

течение длитель-

ного времени.

Таким образом, интенсивность заражения новых членов

по-

пуляции зависит

не

только

от

того, какое количество

инфици-

рованных имеется

настоящее время,

но и от

того, когда

они

были инфицированы.

Для

учета

этого эффекта введем запаз-

дывание,

так что

уравнения динамики приобретут

вид:

(t)/dt

(t)N

- At)

(t)/dt

-aN

(t)N!(t

- At) + y(N -

(t)),

(6)

где коэффициент

постоянный;

величина

имеет смысл

ха-

рактерного времени

от

заражения

до

заражения

цепочке

по-

следовательных инфицирований.

Система дифференциальных уравнений

(6)

может быть

ре-

шена численно

на

компьютере

при

помощи соответствующих

программ. Возможно также

аналитическое

(в

виде формул)

исследование полученных уравнений, которое показывает,

что

как

и в

простейшей модели, решение имеет

вид

затухающих

колебаний около стационарного значения величин

NJQ

Ngg.

159

График

решения

для

малых отклонений имеет такой

же вид

(см.

рис. 2).

Расчет периода колебаний также

дает

величины

порядка

десяти

лет, то

есть результаты модели опять

не

соот-

ветствуют

реальному процессу

ни

количественно,

ни

качест-

венно.

Модель

запаздыванием также

не

является адекватной

для описания эпидемического процесса.

///.

Модель с периодически меняющейся

вероятностью

пе-

редачи инфекции. Для

многих инфекционных заболеваний

ха-

рактерна явная связь активности механизма передачи

со вре-

менем

года,

что

обычно объясняется сезонной активацией

не-

которых путей передачи

или

появлением новых путей. Приве-

дем несколько примеров.

Скорость размножения микроорганизмов

пищевых

про-

дуктах

сильно зависит

от

температуры. Поэтому

при тех же

начальных условиях количество размножающихся

продук-

тах микроорганизмов

теплое время

года

будет

больше,

чем в

холодное. Здесь активизируется постоянно действующий путь

передачи.

В теплое время

года

странах

умеренным климатом появ-

ляются

мухи,

являющиеся дополнительным переносчиком

инфекции.

Весеннее половодье

разлив

рек

существенно

ухудшает

качество речной воды.

этом

случае

также появля-

ется дополнительный путь передачи.

Эти явления можно

учесть

модели переходом

от

постоян-

ного коэффициента

а к

периодическому

периодом

один

год.

Система уравнений

(1) при

этом принимает

вид:

a(t)N

(t)N

- At) -

(3N

(t)

(t)/dt

T(N

(t))

a(t)N

(t)N

- At), (7)

где

a(t)

можно представить

виде:

a(t)

= a

ад

—

постоянная составляющая,

ш^ =

2л/Т^,

Т^ —

период

один

год, (р —

начальная фаза.

Как

и в

предыдущем разделе, усложнение модели связано

со снятием предположения

(4) в

простейшей модели

постоян-

ной

вероятности передачи инфекции

при

встрече инфициро-

ванного

восприимчивого членов популяции.

общем виде

160