Ames W.F., Roger C. Nonlinear equations in the applied sciences. Volume 185
Подождите немного. Документ загружается.


310
Greg
King
and
Ian
Stewart
window, then the eigenvectors above the noise floor should be
jixed
by the isotropy subgroup of the attractor. In practice this will only
hold approximately, but it would be easy enough to devise
a
measure
for the amount to which the eigenvectors deviate from this type of
symmetry: for example, consider the sum of squares of differences
between the entries of the eigenvector and those of its image under
elements
of
the isotropy subgroup.
9
Turbulent Taylor Vortices Revisited
What can we say about the phenomenon of turbulent Taylor vortices,
which we began with, in the light of the above understanding of
symmetric chaos?
There is
a
strong resemblance between the creation of turbulent
Taylor vortices and
a
symmetry-increasing crisis of strange attrac-
tors. What at first sight may seem just an analogy may be
a
com-
plete mat hematical relationship. Although we have discussed mainly
discrete dynamical systems, the same general range of phenomena
should occur
for
continuous flows; and in any case we may discuss
continuous dynamics in terms of
a
hypothetical Poincarb mapping.
The following scenario
was
suggested by Golubitsky in conversation:
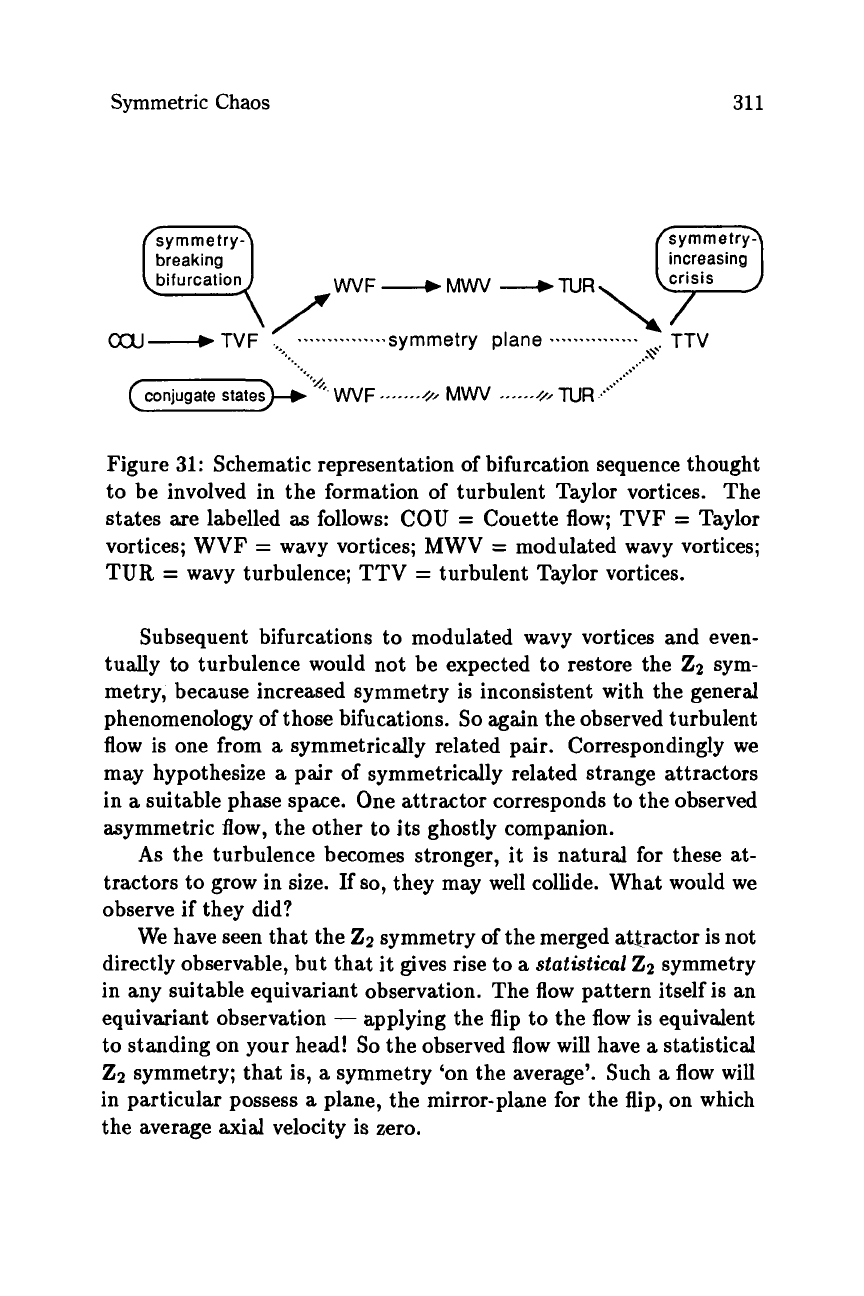
it is summarized schematically in Figure
31.
Focus only on the Z2
‘flip’ symmetry whose
mirror-
plane is the boundary between
a
pair
of adjacent vortices, and which for genuine Taylor vortices leads to
the boundary being planar. The bifurcation from Taylor vortices to
wavy vortices breaks this symmetry, but the system
as
a
whole re-
tains it. Thus for every Zz-symmetry-breaking flow that can occur
there is
a
second flow, its conjugate under the flip, which can
also
occur.
Initial conditions select one from this pair. As it happens,
the two flows for wavy vortices are identical up to
a
phase shift, be-
cause wavy vortices have
a
symmetry that is
a
flip composed with
a
half-period phase shift. This renders the two flows indistinguishable
in the usual experiments, and indeed it is hard to think of an experi-
ment that would distinguish them. However, it is clear on symmetry
grounds that if one
flow
is
a
possible solution to the equations, then
so
must the other be.
Symmetric
Chaos
311
breaking increasing
TTV
WF'MWV
dTUR
symmetry plane
...... .....
....
&
TVF
,,.,
......,........
*S'.
..*'.
"%,,
..*"
WF
.....
-.///
MW
-.---.///
TUR
..
Figure
31:
Schematic representation of bifurcation sequence thought
to be involved in the formation of turbulent Taylor vortices. The
states are labelled
as
follows: COU
=
Couette flow; TVF
=
Taylor
vortices; WVF
=
wavy vortices; MWV
=
modulated wavy vortices;
TUR
=
wavy turbulence; TTV
=
turbulent Taylor vortices.
Subsequent bifurcations to modulated
wavy
vortices and even-
tually to turbulence would not be expected to restore the
22
sym-
metry, because increased symmetry is inconsistent with the general
phenomenology of those bifucations.
So
again the observed turbulent
flow is one from
a
symmetrically related pair. Correspondingly we
may hypothesize
a
pair
of
symmetrically related strange attractors
in
a
suitable phase space. One attractor corresponds to the observed
asymmetric
flow,
the other to its ghostly companion.
As
the turbulence becomes stronger, it is natural for these at-
tractors to grow in size.
If
so,
they may well collide. What would we
observe if they did?
We have seen that the
22
symmetry
of
the merged aqractor is not
directly observable, but that it gives rise to
a
statistical
22
symmetry
in any suitable equivariant observation. The
flow
pattern itself is an
equivariant observation
-
applying the flip to the flow is equivalent
to standing on your head!
So
the observed flow will have
a
statistical
22
symmetry; that is,
a
symmetry 'on the average'. Such
a
flow will
in particular possess
a
plane, the mirror-plane for the flip, on which
the average axial velocity is zero.

312
Greg King and Ian Stewart
This is precisely what Fenstermacher
et
al.
[15]
have observed in
turbulent Taylor vortex flow.
Indeed more may be true.
Experiments in Swinney’s labora:
tory (communicated to us by Dan Lathrop) suggest that the
entire
sequence of symmetry-breaking bifurcations from Couette
flow
to
modulated wavy vortices may be restored in
a
corresponding series
of
crises
(or
similar transitions) of chaotic attractors.
The symmetry-increasing crisis model shows that the most puz-
zling aspect of the formation of turbulent Taylor vortices
-
the in-
crease in pattern
as
the turbulence becomes stronger
-
is actually
natural. Only by growing in size can strange attractors collide to
combine their symmetries.
There are strong analogies between this scenario, the bifurcations
of the cubic logistic map, and those of the Van der Pol-Duffing
os-
cillator reported above. The general changes in symmetry, and the
changes from order
to
chaos, are essentially identical in all three.
The differences lie in the fine detail
of
the dynamics.
It would be interesting to test this idea. It does not appear
fea-
sible to do
so
by way of numerical simulations: we are looking at
a
turbulent time-dependent three-dimensional flow, beyond the ca-
pabilities even of
a
supercomputer. However, it should be relatively
easy
to
test it experimentally, by using
a
22-equivariant time se-
ries. The natural way to achieve this is to use two laser probes,
symmetrically placed above and below the ‘boundary’ between adja-
cent turbulent Taylor vortices, arranged
to
measure the
axial
velocity
(or
some velocity with
a
strong axial component). Indeed two beams
could be produced from
a
single laser using
a
beam-splitter; however,
two detectors might be necessary. The signals could be processed by
an equivariant version of the method of Broomhead and King
[6],
as
described above.
Acknowledgements
We are grateful
to
Peter Ashwin, Sofia Castro, Mike Field, Marty
Golubitksy, Gabriela Gomes, Maciej Krupa, Dan Lathrop, Robert
MacKay, and Mark Roberts for permission to include unpublished
ideas of theirs and to describe work in progress, and
for
helpful dis-

Symmetric
Chaos
313
cussions about symmetric chaos. Many of our pictures were drawn
using the dynamical systems package
Kaos
for
SUN
workstations,
written by John Guckenhimer and Swan Kim. The first author's
research
was
partially supported by
a
grant from the Science and
Engineering Research Council. Part of this paper derives from work
done by the second author when visiting the Institute for Mathemat-
ics and its Applications
at
the University of Minnesota,
to
whom he
is grateful for financial support and hospitality.
Bibliography
(11
P.Ashwin, Symmetric chaos in systems of three and four forced
oscillators,
Nonlinearity,
to appear.
(21
P.Ashwin, G.P.King, and J.W.Swift, Three identical oscillators
with symmetric coupling,
Nonlinearity,
to appear.
[3]
J.S.Birman and R.F.Williams, Knotted periodic orbits in dy-
namical systems
I:
Lorenz equations,Topology
22
(1983) 47-82.
[4]
R.Bowen,
On
Aziom
A
Difleomorphisms,
CBMS Regional Con-
ference Series in Mathematics
35
,
Amer. Math. SOC., Provi-
dence RI
1978.
[5]
A.Brandstater and H.L.Swinney, Strange attractors in weakly
turbulent Couette-Taylor
flow,
Phys. Rev.
A
35
(1987) 2207-
2220.
[6]
D.S.Broomhead and G.P.King, Extracting qualitative dynamics
from experimental data,
Physica
20D
(1986) 217-236.
[7]
D.S.Broomhead and G.P.King, On the qualitative analysis of
experimental dynamical systems, in
Nonlinear Phenomena and
Chaos,
(ed. S.Sarkar), Adam Hilger, Bristol
1986, 113.
[8]
S.Castro,
Ezperiments
in
Nonlinear Dynamics: an attmctor
of
the modified van der
Pol
oscillator (with quintic characteristic),
Nonlinear Systems Laboratory report, Univ.
of
Warwick
1990.

314
Greg
King
and
Ian
Stewart
[9]
P.Chossat and M.Golubitsky, Iterates of maps with symmetry,
SIAM
J.
Math. Anal
19
(1988) 1259-1270.
of chaotic attractors,
Physica
D
32
(1988) 423-436.
namical Systems,
Birkhauser, Boston
1980.
[lo]
P.Chossat and M.Golubitsky, Symmetry- increasing bifurcation
[ll]
P.Collet and J.-P.Eckmann,
Itemted Maps
of
the Interval as Dy-
[12]
W.D.Crowe, R.Hasson, P.J.R.ippon, and P.E.D. Strain-Clark,
On the structure of the Mandelbar
set,
Nonlinearity
4
541-554.
[13]
P.CvitanoviC,
Universality in Chaos
(2nd ed.), Adam Hilger,
Bristol
1989.
[14]
R.L.Devaney,
An Introduction to Chaotic Dynamical Systems,
[15]
P.R.Fenstermacher, H.L.Swinney, and J.P.Gollub, Dynamical
instabilities and transition to chaotic Taylor vortex
flow,
J.
Fluid
Mech.
94
(1979) 103-128.
2nd ed., Addison-Wesley, Redwood City CA
1989.
[16]
M.J.Field and M.Golubitsky, to appear.
[17]
J.G.Franjioni, C.-W-Leong, and J.M.Ottino, Symmetries within
chaos:
a
route to effective mixing,
Phys. Fluids
A
1
(1989) 1772-
1783.
[18]
S.T.Gaito and G.P.King, Chaos on
a
catastrophe manifold, in
Quantitative Measures
of
Dynamical Complexity,
NATO ARW
Series, Plenum Press, New York
1990.
[19]
M.Golubitsky, D.G.Schaeffer, and I.N.Stewart,
Singularities and
[20]
M.G.M.Gomes and G.P.King,
Bifurcation analysis
of
a chaotic
Van der Pol-Dufing oscillator,
preprint, University
of
Warwick
1990.
Gmups in Bifurcation Theory
v01.2, Springer,
New
York
1988.
[21]
C.Grebogi, E.Ott, F.Romeiras, and J.A.Yorke. Critical expo-
nents
for
crisis induced intermittency,
Phys. Rev.
A
36
(1987)
5365-5380.

Symmetric
Chaos
315
[22]
J.Guckenheimer and P.J.Holmes,
Nonlinear Oscillations, Dy-
namical Systems, and Bifurcations of Vectro Fields,
Applied
Mathematical Sciences
42
,
Springer, New York
1983.
[23]
P.J.Holmes, A nonlinear oscillator with
a
strange attractor,
Phil.
%ns.
R.
Soc.
London
A
292
(1979) 419-448.
[24]
M.Kitano, T.Yabuzaki, and T.Ogawa, Symmetry- recovering
crises
of
chaos in polarization-related optical bistability,
Phys.
Rev.
A
29
(1984) 1288-1296.
[25]
M.Krupa and R.M.Roberts, in preparation.
[26]
R.S.MacKay and C.Tresser, Transition to topological chaos
for
[27]
J.Milnor,
Remarks on iterated cubic maps,
preprint, SUNY
circle maps,
Physica
19D
(1986) 206-237.
Stonybrook Inst. Math. Sci.
1990.
[28]
N.H.Packard, J.P.Crutchfield, J.D.Farmer, and R.S.Shaw, Ge-
ometry from
a
time series,
Phys. Rev. Lett.
45
712-.
ping,
Phys. Lett.
A
135
(1989) 190-196.
Modelling
4
(1983) 9-25.
map,
Progr. Theomt. Phys.
78
(1987) 305-315.
[29]
E.Piiia and E.Cantoral, Symmetries of the quasicrystal map-
[30]
T.Rogers and D.C.Whitley, Chaos in the cubic mapping,
Math.
[31]
H.Sakaguchi and K.Tomita, Bifurcations of the coupled logistic
[32]
Science and Engineering Research Council,
The Remarkable
World of Nonlinear Systems,
SERC
,
Swindon
1989.
[33]
K.G.Szab6 and T.Tdl, On the symmetry-breaking bifurcation of
chaotic attractors,
J.
Stat. Phys.
64
(1989) 925-948.
[34]
F.Takens, Detecting strange attractors in turbulence, in
Dynarn-
ical Systems and Turbulence, Warwick
1980,
Lecture Notes in
Math.
898
(eds. D.A.Rand and L.-S. Young), Springer, New
York
1981, 366-381.
This page intentionally left blank

Backlund and Reciprocal
Transformations: Gauge
Connect
ions
B.G. Konopelchenko
Institute
of
Nuclear Physics
630090,
Novosibirsk
USSR
C. Rogers
Loughborough University
of
Technology,
U.K.
and
University
of
Waterloo, Canada
1
Introduction
The r6le
of
Backlund Transformations
(BTs) is well-
established in the analysis of nonlinear evolution equa-
tions amenable to the
Inverse Scattering Transform
(IST). Thus, in particular, BTs are routinely used to con-
struct nonlinear superposition principles whereby multi-
soliton solutions may be generated.
BTs
can be con-
structed by
a
variety
of
means. Classical, jet-bundle
and bilinear operator methods are described, in detail,
in Rogers and Shadwick
[l].
In the context of integrable
systems, perhaps the most direct approach is via the
so-
called
Dressing Method
(DM) (Zakharov and Shabat
[2]). This is linked to the
Classical Darboux Transfor-
mation
(CDT) introduced in 1882 which generates
so-
lutions to related Schrodinger equations (Darboux
[3]).
The connection has been described by Levi, Ragnisco
and Sym
[4].
Therein, the analogue of the
CDT
for the
Zakharov-Shabat-AKNS spectral scheme was presented.
The relation between the
BT
and DM methods for
1
+
1
Nonlinear Equations in the Applied Sciences
317
Copyright
0
1992 by Academic Press,
Inc.
All
rights
of
reproduction in
any
form
reserved.
ISBN 0-12-056752-0

318
B.
G.
Konopelchenko
and
C.
Rogers
-dimensional nonlinear integrable systems has been de-
tailed by Levi, Ragnisco and
Sym
in
[5].
Decomposition
of
BTs into the product of commut-
ing
elementary
Backlund
Transformations
(EBTs) has
been treated by Konopelchenko,
[6-81
and Calogero and
Degasperis
[9].
Generalised lattices of solutions which in-
corporate the Bianchi lattices associated with the stan-
dard BTs may be thereby constructed
[8].
Certain classes
of
BTs
constitute Abelian free groups, the generators of
which are the EBTs
[6].
Extension to higher dimensions of the established
methods developed for nonlinear integrable equations in
1
+
I-dimensions is
a
subject
of
current research.
BTs
have been shown
to
play
a
key r6le in this area. Thus,
until recently, the only known localized objects in
2
+
1-
dimensions were the so-called lump solutions which de-
cay algebraically at infinity. However, in an important
new development, BTs have been exploited by
M.
Boiti
and his co-workers
to
derive truly two-dimensional coher-
ent structures which decay exponentially in all directions
[lo].
The associated nonlinear superposition principle
was used to study the scattering properties
of
these lo-
calized phenomena. The
2
+
I-dimensional
BTs
employed
were constructed by the
DM
based on appropriate gauge
transformations (Boiti, Konopelchenko and Pempinelli
[ll]).
The
DM
had been earlier used in
2
+
1-dimensions
by Levi, Pilloni and Santini
[12]
to generate auto-BTs for
the Kadomtsev-Petviashvili
(KP),
two-dimensional three
wave and Davey-Stewartson
(DS)
equations, in turn.
Gauge transformations, in conjunction with reciprocal
transformations, also play an important part in links be-
tween scattering schemes associated with classes
of
non-
linear integrable systems. Here, reciprocal transforma-
tions in
1
+
1-
and
2
+
1-
dimensions are introduced. The
link between the
1
+
1-dimensional
ZS-AKNS
and WKI

Backlund and Reciprocal Transformations: Gauge Connections
319
spectral schemes via
a
combination
of
gauge and recip-
rocal transformations is established.
A
reciprocal invari-
ance
of
the
1
+
1-dimensional Dym hierarchy is also exhib-
ited. In
2
+
I-dimensions,
a
reciprocal link between the
KP
and
a
Dym-type equation is revealed. This allows
a
novel invariance of the latter to be constructed.
2
The Dressing Method
The inverse spectral transform
(IST)
is now a well-
established tool in the investigation
of
initial value prob-
lems for
a
wide class of nonlinear equations
[13-171.
The
key to the
IST
method is the correspondence between
a
nonlinear system
and an associated pair of
linear
prob-
lems
where the operators
Ll
and
L2
are parametrized by
a
certain set of functions
ul(xl,.
. .
,
xn),
. . .
uk(x1,.
. .
,
xn)
of the independent variables
xl,.
. .
,
z,.
The compatibil-
ity
of
the two linear problems
(2.1),
(2.2),
namely, the
commutativity condition
[Ll,
L2]
=
0
(2.3)
produces the nonlinear system for the
ui
which
is
amen-
able to the IST. The standard IST method involves the
application of both the direct and inverse spectral meth-
ods to the linear system
(2.1)
-
(2.2)
to
solve initial value
problems for the associated
integrable
nonlinear system.
Dressing transformations
