Ames W.F., Roger C. Nonlinear equations in the applied sciences. Volume 185
Подождите немного. Документ загружается.


320
B.
G.
Konopelchenko
and
C.
Rogers
applied to the inverse scattering formulation (2.1)
-
(2.2)
were originally introduced by Zakharov and Shabat [2]
and provide, in particular, an incisive method for the con-
struction of auto-BTs admitted by the nonlinear equa-
tions associated with the commutativity condition (2.1).
Thus, it
is
required that the dressing transformations pre-
serve the form
of
the operators
L1
and
L2
so
that, since
it follows that the functions
ui,
. .
.
,
ui
obey the same non-
linear system as the functions
u1,.
. .
,
uk.
Accordingly, the
dressing transformations (2.4)
-
(2.5) convert solutions
of
a
given integrable nonlinear equation
as
generated
by
the
compatibility condition (2.3), into solutions of the same
equation.
In order to extract explicit dressing transformations,
it is necessary to assume specific forms for the dress-
ing (gauge) operator
G.
Thus, if one chooses the op-
erator
G
as
an
appropriate Volterra-type integral opera-
tor then one arrives at the well-known Gelfand-Levitan-
Marchenko linear integral equations and the correspond-
ing reconstruction formulae for the potentials.
The ini-
tial value problem for the underlying nonlinear integrable
equations may then, in principle, be solved. The details
of this approach to the
IST
via dressing transformations
are set down in [2,14]. In what follows, it is shown how
the
DM
may be used to construct auto-BTs and associ-
ated nonlinear superposition principles for nonlinear in-
tegrable equations amenable to the inverse scattering for-
mulation (2.1)
-
(2.2).
3
Biicklund Transformations
via
the
Dressing
Method

Backlund and Reciprocal Transformations: Gauge Connections
321
The use of another ansatz for
G
allows the construction
via the dressing transformations (2.4)
-
(2.5) of associ-
ated auto-BTs.
This method
of
construction was origi-
nally proposed in [12,
19,
201.
Here, we consider the application of the
DM
to the con-
struction
of
auto-BTs for nonlinear evolution equations
associated with the Zakharov-Shabat
(2s)
and Ablowitz-
Kaup-Newell-Segur
(AKNS)
spectral problem viz, [2,
151,
La$=
[$
-V(x,t;h)]
(;:)
=0,
V=
(
AB
)
(3.2)
C
-A
where
X
is
a
(spectral) parameter,
+i
i
=
1,2
are eigen-
functions,
q(x,
t)
and
r(z,
t)
are generally complex-valued
functions and
V(z,t;
A)
is
a
2
x
2
matrix with polyno-
mial dependence on
A.
The compatibility condition (2.3)
with different
V(x,t;
A)
gives rise to various systems of
nonlinear evolution equations for
q(x,
t)
and
r(x,
t).
One
important system is that corresponding to
2X2i
-
iqr
2Xir
-
irx
2Xiq
+
iq,
-2X2i
+
iqr
v=
(
(3.3)
namely
(3.4)
iqt
+
qxx
-
2qrq
=
0
irt
-
rxx
+
2qrr
=
0
where it is assumed that
q,r
---,
0
as
I
x
I+
00.
In the
case
q
=
-F,
the system (3.4) reduces to the nonlinear
Schrodinger
(NLS)
equation
iqt
+
qxx
+
2
I
q
l2
q
=
0.
(3.5)

322 B.
G.
Konopelchenko
and
C.
Rogers
Other specializations of
V
leading to nonlinear evolution
equations of importance are given in
[l].
The ansatz for
G
which give rise to
BTs
adopts the
form [12,2O]
n
k=O
where
gk(2,t)
are
2
x
2
matrix-valued functions.
The simplest
BT
corresponds to the most elementary
G
of
the type
(3.6),
namely, the
lSt
order matrix polynomial
To
determine the explicit form
of
the auto-BT corre-
sponding to
(3.7))
it
is
noted that the
ZS-AKNS
system
may be written as
$z
=
Ulc,
$t
=
vlc,
where
u
=
A03
+
P
(3.9)
with
(3.10),
(3.11)
0
-1
Under the dressing transformation (2.4)
-
(2.5)
the
ZS-AKNS
system becomes
(3.12)
$;
=
U'$'
$;
=
v'lc,'

Backlund
and
Reciprocal Transformations: Gauge Connections
323
where
U'
=
GUG-l+ G,G-l,
(3.13)
V'
=
GVG-I
+
GtG-'.
(3.14)
In particular, substitution of (3.9) into (3.13) produces
the following system of equations for
go
and
91:
[03,s1]
=
0,
-
dX
-
[03,go]
+
g1P
-
P'g1
=
0,
(
3.1 5a)
(3.15b)
as1
ago
-
+
goP
-
P'go
=
0,
dX
where
PI=(;
z).
(3.15~)
(3.16)
The solution
of
the system (3.15a
-
3.15~)
is
readily
obtained if
(3.17)
In this case, if
go
=
(goij)
then (3.15b) gives
go12
=
-7Q
1'
,
go21
=
-7'
1
(3.18), (3.19)
while substitution
of
these expressions into the diagonal
part of the matrix equation (3.15~) yields
go11,z
=
0,

324
B.
G.
Konopelchenko
and
C.
Rogers
where
A0
is
a
complex constant. Further, with the use
of
(3.20)
-
(3.21), the off-diagonal part
of
(3.15~) yields
(q‘r’
-
qr)dx‘
+
2Aoq’
-
2gOllq
=
0,
(3.22~)
(q’r‘
-
qr) dx’
-
2x07-
+
2gOllr‘
=
0,
(3.22b)
and elimination
of
the integral terms in (3.22) gives
Hence, (3.22a,
b)
yield, with
go11
=
-1
(3.23)
The relations (3.24) constitute the spatial part
of
the
auto-BT associated with the dressing (gauge) transfor-
mation with
.
(3.25)
tr
A0
-
iq’r
+(
--
00
G:=GA,,(A)=h(O
(1)
They
are
generic to the whole class of nonlinear evolution
equations connected with the linear system (3.1).
On the other hand, the temporal part of the BT
de-
pends on the particular member
of
the
ZS-AKNS
class:
thus, it
is
determined
by
the form
of
V.
In particular,

Backlund and Reciprocal Transformations: Gauge Connections
325
with the specialization
(3.3)
corresponding to the cou-
pled NLS system
(3.4),
the relation
(3.14)
produces
'I-
2-
.
dq'
-
q'
(q'r'
+
qr
-
-T-
8q')
-
2XOZ
%'
-
2z aq
=
o
at
(
2q
ax
at
ax
2-
+
r
q'r'
+
qr
+
1
I-
a,)
-
2XOZ
-
2az
=
0
dr
art
(3.26)
The relations
(3.26)
represent the temporal part
of
the
auto-BT for the coupled
NLS
system
(3.4)
corresponding
to the dressing transformations
G
=
GY)(X).
Another simple BT corresponds to the choice
91=(;
;)
(3.27)
in
(3.15).
Proceeding as in the previous
case,
it is readily
seen that the associated dressing (gauge) transformation
is
(3.28)
-1
G
:=
Gl;b)(X)
=
X
(:
;)
+
(
with corresponding generic spatial part
of
the auto-BT
(3.29)
&7
1'2
-
-
p'
q
+
2poq
+
2q'
=
0,
art
1
'2
ax
-
+
2r
q
-
2pOr'
-
2r
=
O
dX
The temporal part
of
the
BT
in the case
of
the coupled
NLS system
(3.4)
is given by
(3.14)
together with
(3.3)

326
B.
G.
Konopelchenko
and
C.
Rogers
as
34
at
ax
ax
ax
art ar
z--q
qr +q~--~r-
-2po--2-=0
i?
+r/
(q/r/
+
qr
+
+qz
-
2po-
-
2-
=
o
(3.30)
at
")
ax ax
The
BTs
associated with the gauge (dressing transfor-
mations)
GP:(X)
and
G(,J(X)
play an important rde in the
analysis
of
the nonlinear evolution equations associated
with the
ZS-AKNS
spectral problem
(3.1)
-
(3.2).
They
are termed
elementary
BTs and are here denoted by
el\';
and
Bp'
respectively. It
is
readily shown that any BT
corresponding to
a
gauge operator
of
the form
(3.6)
may
be obtained
as
an appropriate product of several
GY;(X)
and
Gjl2,)(X)
with different
A0
and
po.
In particular, the
general operator
G
linear in
X
as
given by
(3.7)
can be
represented
as
the product
of
two
elementary
gauge
op-
erators
GYJ(X)
and
G;J(X).
The associated elementary
BTs may likewise be composed to generate broad classes
of
BTs
of the type
i=
1
k=l
(3.31)
The sequential application of
GY;(X)
and
G(,J(X)
to
1c,
yields

Backlund and Reciprocal Transformations: Gauge Connections
327
(3.32)
while, the reversed order composition gives
(3.33)
In the above, we adopt the notation
2 12
412
:=
B,oB:040
7
421
:=
B,o
@po
40
7
7-12
:=
B;,B:,rO
7
7-21
:=
B:oBporo
(3.34)
41
:=
B:,Qo
7
7-2
:=
B2,,7-0.
2
It
is
seen
that
commutativity of the action of the el-
ementary gauge transformations is assured by the two
conditions
qxo
-
Po)
421
-
40
=
?+&
(3.35)
(3.36)
It
is noted that
(3.35)
-
(3.36)
impose the simple relation
-2po
-
PO)
TI2
-
To
=
p+&
fd40
-
421)
=
Ql(7-12
-
7-0)
(3.37)
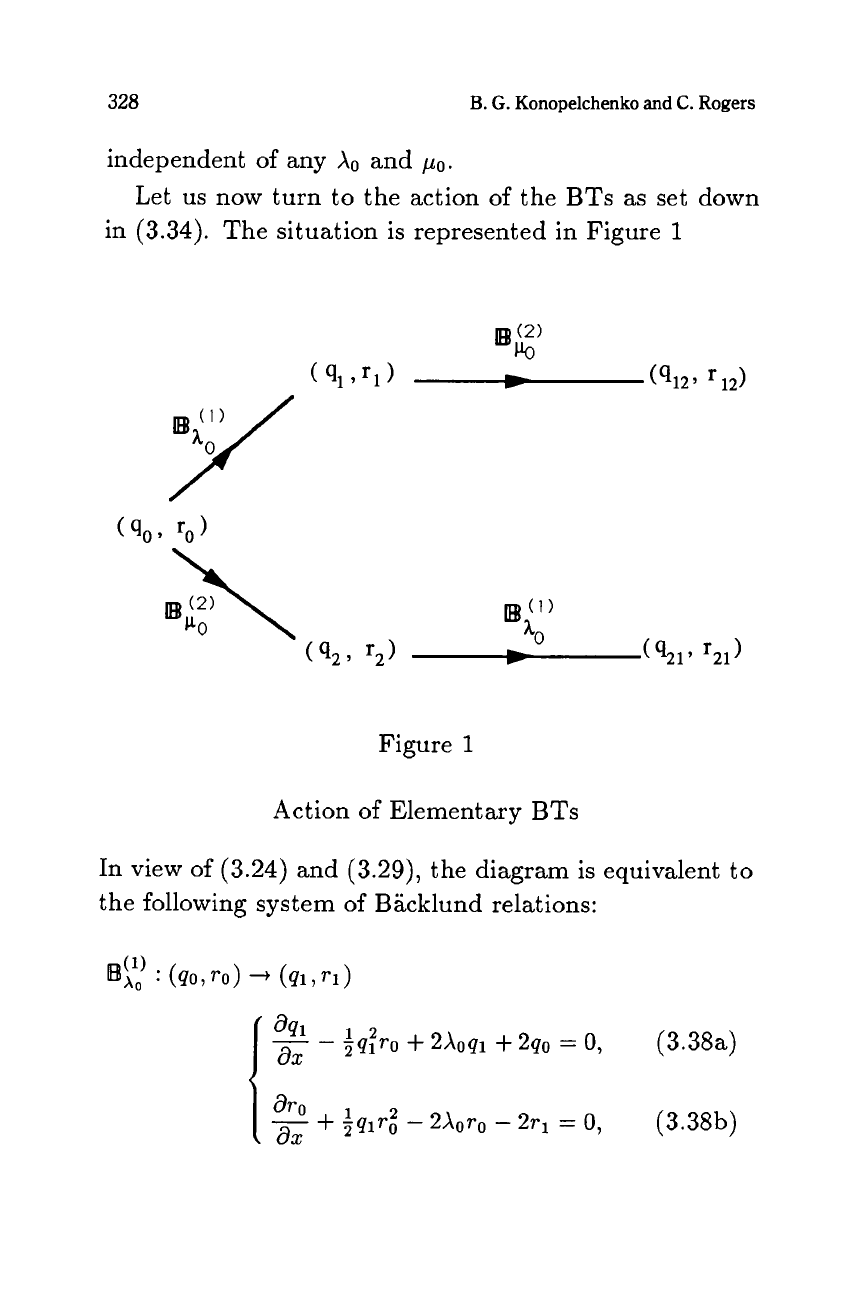
328
B.
G.
Konopelchenko
and
C.
Rogers
independent
of
any
A0
and
po.
in
(3.34).
The situation
is
represented
in
Figure
1
Let
us
now
turn to the action of the BTs as set down
Figure
1
Action of Elementary BTs
In view of
(3.24)
and
(3.29),
the diagram is equivalent to
the following system
of
Backlund relations:

Backlund and Reciprocal Transformations: Gauge Connections
329
1r12q;
+
2poq1
+
2q12
=
0,
{
:-21
ax
+
p1241
2
-
2po7-12
-
27-1
=
0,
(3.39a)
(3.39b)
(3.40a)
(3.40b)
(3.41a)
(3.41b)
Comparison
of
(3.38a) and (3.39a) yields
12
-5~1r0
+
2x041
+
2qo
=
-+~12~:
+
2~0~1
+
2412,
(3.42)
while, coiiiparison
of
(3.40b)
aiid (3.41a) gives
5r2q0
12
-
2por2
-
2ro
=
5q21r;
1
-
2X07-2
-
2r21, (3.43)
