Ames W.F., Roger C. Nonlinear equations in the applied sciences. Volume 185
Подождите немного. Документ загружается.


460
R.
W.
Ogden
and the inequalities (111) show that the solution branches corre-
sponding to
A
#
1
are stable for
ni2
>
1
and unstable for
ni2
<
1.
Moreover, the symmetrical solution
X
=
1
is unstable for
t’
>
tt.
We
emphasize that bifurcation is predicted for
every
form of
14’
consis-
tent with the requirement Ik”(1)
=
2p
of the classical theory. We
illustrate these results in Figure
2.
Energy
Considerations
For
the dead-load traction boundary-value problem considered here
the energy functional
(42)
can be written,
on
use
of
the divergence
theorem,
as
arguments being omitted. Since the deformation is homogeneous it
suffices to consider the integrand of (115), which we write
as
3
E
=
IY
-
tr(SA)
=
IY
-
Ct!Xi
(116)
i=l
for an isotropic material. This
is
the energy per
unit
volume of
B,.
The additional term associated with the incompressibility constraint
is omitted since it plays
no
part in the following analysis.
The two-dimensional counterpart of
(
1
lG), obtained by
a.
niiiior
change in the definition of
E
(A3
is
replaced by
A3
-
l), can be
expressed
as
E
=
1V(X1,X2,1)
-
t;x,
-
t;x,
(117)
on
taking
A3
=
1.
Now
let
E,,
and
E,
respectively denote the
energies (per unit cross-sectional area and per unit length in the
3-
direction) on the asymmetric and symmetric soh tion paths discussed
above. Then
E,,
=
1/2l(X)
-
t’(X
+
X-’),
E,
=
-2f.’,
and hence
E,,
-
E,
=
l@(X)
-
t’(X
+
A-’
-
2).

Nonlinear Elasticity
461
On
the asymmetric path we can regard
X
as
a
function of
t1
through
(107); note that
E,,
=
E,
when t'
=
t:.
On
use of (107) we then
obtain
(119)
d
1
-(&,
-
E,)
=
-(AT
-
A-3)2
5
0.
dt
1
This shows that on
a
stable (asymmetric) path of deformation with
t'
increasing from
ta
the energy is less than on the corresponding
symmetric path. Thus, the asymmetric path provides the (global)
energy-minimising solution. In particular, near
t'
=
t:,
we have
7
(120)
where
7
is given by (110). If
7
>
0
the asymmetric solution is stable
and branches to the right, while
if
11
<
0
it is unstable and branches
to the left (Figure 2). In the latter case the symmetric path provides
the energy minimiser.
To
be more explicit, if we take
m
=
2 in (113) then
7
>
0,
1
2
t'
=
-p(A
+
A-'),
and (118) reduces to
(
122)
1
P
E,,
-
E,
=
--(p
-
t')2.
For
rn
=
2 the strain-energy function (112) is called the
neo-Hookeun
strain-energy function and this provides
a
model for the behaviour
of rubber-like solids at moderate deformations.
For further discussion of this and related problems we refer to,
for example, [3,10,14,15,16,19].
Clearly, the degree of non-uniqueness in the relation between
tf
and
A;,
as reflected in that between
S
and
A
will have implications
for the solution of inore general boundary-value problems than the
homogeneous dead-load problem discussed in this section. Reference
to other problems in which non-uniqueness is evident
can
be found
in, for example,
[6,14].
In
Section
5,
we consider one further ex-
ample of the onset of bifurcation from
a
homogeneously-deformed
configuration.

462
R.
W.
Ogden
5
Surface Deformations of a Half-space
We now consider
a
pure homogeneous deformation of the form
and we suppose that
B
corresponds
to
the region
22
<
0
with bound-
ary
22
=
0.
Let tl,t2,t3 denote the principal components
of
the
Cauchy stress tensor
T.
An incremental deformation of the form (47)
is superimposed on the above deformation, and we denote the dis-
placement vector
x
by
u.
At this point we update the reference
configuration
so
that
B,
coincides with
B
and we rega.rd u
as
a
func-
tion of
x
through (47) and the inverse of
(1).
Let
F
=
gradu denote the
displacement gmdient,
where grad is
the gradient operator in
B.
The components
T;j
=
ih~/Oxj
of
r
are
denoted by
u;j
for compa.ctness, where
,i
represents
a/&i.
We also
take the material to be incompressible
so
that
X1X2X3
=
1,
while, for
the incremental deformation,
The updating of the reference configuration modifies the incre-
mental stress-deformation relation (53), which
now
becomes
So
=
&r
+
p~
-
ji,
(124)
where the zero subscript indicates evaluation in
B.
In
the
absence of
body forces, the equilibrium equations (54) become
divSo
=
0.
(125)
while the incremental traction
Sin
per unit area
of
3B
has compo-
nents
(127)
1
Sojinj
(dojilk
+
P6jkS;I)uk,/nj
-
fin;.

Nonlinear Elasticity
463
For an incompressible material, the components
of
4
a.re given
by
Ahijkr
=
X;Xkd,1JI;I
(128)
(no summation), where the componeiits of
A'
are obtained from
(81)-(84)
subject to
X1X2X3
=
1.
We
also note t1ia.t the strong ellip-
ticity condition
(45)
becomes
dhj;rknjnimimk
>
0
(129)
for all non-zero vectors
m
and
n
satisfying the condition
m
.
n
=
0
imposed by the iiicompressibility constraint.
We now specialize to two-dimensional incremental deformations
with ug
=
0
and
~1,212
independent
of
23
so
that
(123)
reduces to
111,l
t
1L2,2
=
0,
(130)
from which we deduce the existence
of
a
function
11,
such that
Substitution
of
(131)
into the appropriate specia1iza.tion of
(125)
yields (after some rearrangement
[7])
an equation for
~,
namely
4JJ111
t
'2P11,,1122
t
74,2222
=
0
.2'2
<
0.
(132)
If
we take the incremental boundary traction to vanish on
8B
then
use of
(127)
leads to the following boundxy conditioiis
011
,$:
(2P
+
Y
-
t2)$,112
+
Y$,222
=
0
on
22
=
0.
(134)
See
[7]
for details in
a
slightly more general setting. In
(132)-(134)
we have introduced the notation

464
R.
W.
Ogden
The strong ellipticity condition
(129),
appropriately specialized to
the two-dimensional situation considered here, reduces simply to
a
>
0,
p
>
-(ay)f.
(137)
We seek incremental deformations which decay
as
22
-,
-00;
such
a
deformation is regarded as
a
surjace deformation.
For
sim-
plicity, we take
+
to have the form
where
A,
s
and
k
are constants. Substitution into
(132)
yields
a
quadratic equation for
s2,
namely
ys4
-
2ps2
+
(Y
=
0.
(139)
Denoting the roots of
(139)
by
s:
and
s;,
we deduce that
(140)
SlS2
22
=
a/y
=
x;/x;.
Taking
s1
and
s2
to
be the solutions
of
(139)
with positive real part,
we write the general solution of
(132)
with the required properties
in the form
FkX1
7
(141)
$,
=
(AeSlkQ
t
Bes'2b
where
B
is another constant.
the expression
(141)
leads to
When substituted into the boundary conditions
(133)
and
(134)
(y~l
2
t
y
-
t2)A
t
(7s;
+
y
-
t2)B
=
0,
(142)
(143)
For
a
non-trivial solution A,
B
of
these equations the determinant
of
coefficients must vanish. After elimination of
a
factor
s1
-
s2,
whose
vanishing yields
a
trivial solution, we obtain
(2p
t
y
-
t2
-
~s;L)s~A
+
(2p
t
y
-
22
-
~s;)s~B
=
0.
y"
t
2(P
t
Y
-
tz)(ra)i
-
(7
-
t2j2
=
0.
(
144)

Nonlinear Elasticity
465
Thus, surface deformations with
$
given by
(141)
are possible for
values of
Ai7A2,A3
and t2 satisfying
(144).
In particular, when the
normal surface stress t2 vanishes equation
(134)
becomes
y(0
-
7
+
2(a/y)f(P
+
y)}
=
0.
(145)
In
the undeformed stress-free configuration
y
=
p
and tlie fa.ctor in
braces in
(145)
is
$1.
Since
p
is positive then, by continuity, we must
have
y
>
0,
0
-
y
+
2(a/y)qP
+
y)
>
0
(146)
for surface deformations to be excluded on
a
pa,th of homogeneous
deformation from this stress-free configuration. We note that the in-
equa.lities
(146)
imply the strong-ellipticity inequalities
(137).
When
t2
#
0
the corresponding exclusion condition
is
obta.ined by rep1a.c-
ing
'
=
'
in
(144)
by
'
>
'
,
and this yields
a
range of values for tz
which simplifies to
-2p
<
t
<
2p
when tlie stress
is
hydrostatic
(t;
=
t,
i
E
{1,2,3}).
In
terms of the strain-energy function
lV,
expressed
as
a
function
of two independent stretch variables through
VV(A,,A3)
=
W(A~,X,1A,',A3),
(147)
the second inequality in
(146)
becomes siinply
A
further specialization, using the notation
(103)
with
A3
=
1,
en-
ables
(148)
to be written
x3i/Vii(x)
+
W(A)
>
0,
(149)
while
y
>
0
requires that
r4q
A)
(A
-
1)
>
O.
Particular cases of the criterion
(144)
for the onset of surface
deformations (or instabilities) have been obtained
by
a
number
of
466
R.
W.
Ogden
-
t
2
0
-1
-2
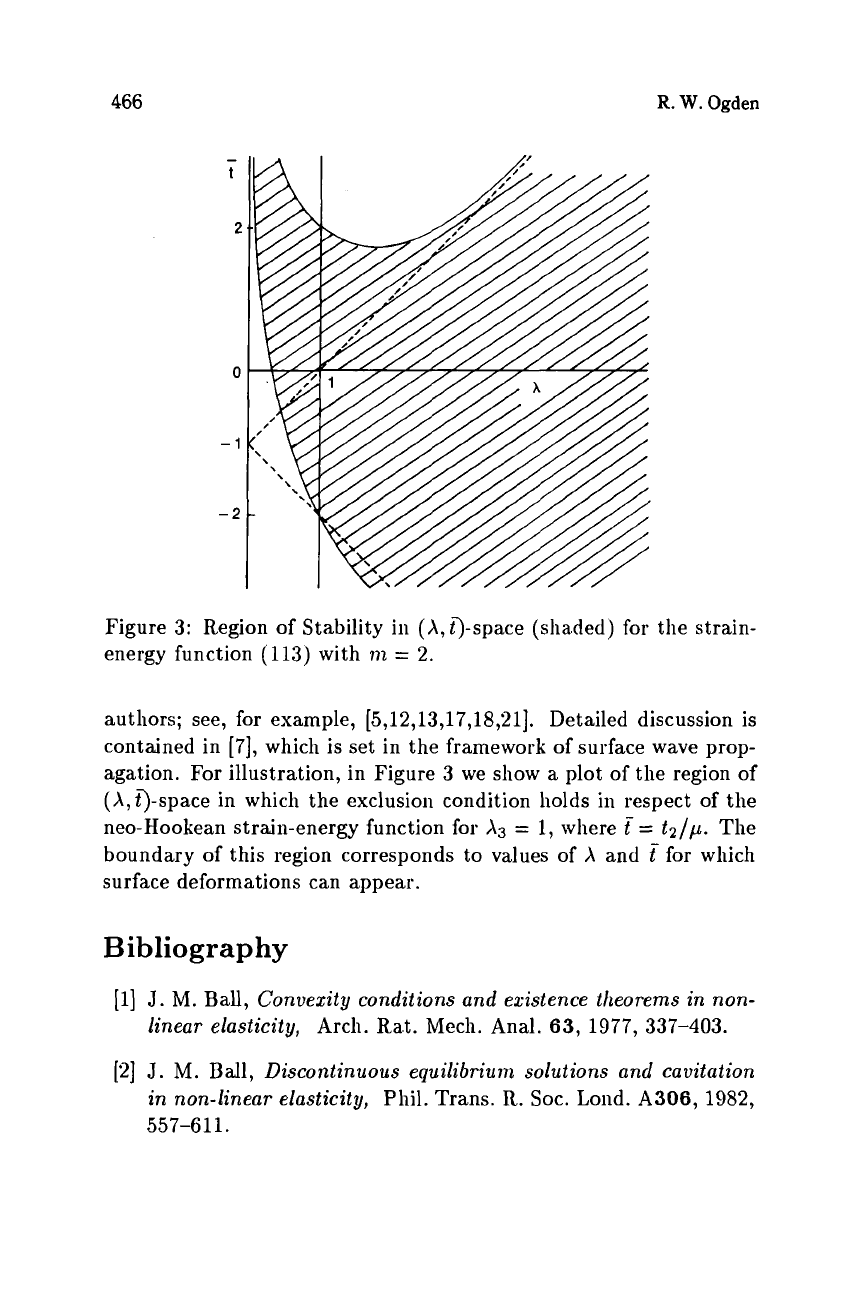
Figure
3:
Region
of
Stability in (X,q-space (sha.ded)
for
the strain-
energy function
(113)
with
in
=
2.
authors;
see,
for example,
[5,12,13,17,18;21].
Detailed discussion is
contained in
[7],
which
is
set in the framework of surface wave prop-
agation.
For
illustration, in Figure
3
we show
a
plot of the region of
(A,
@space in which the exclusion condition holds
in
respect
of
the
neo-Hookean strain-energy function for
=
1,
where
f
=
tz/p.
The
boundary
of
this region corresponds to values of
X
and
t
for which
surface deformations can appear.
Bibliography
[l]
J.
M.
Ball,
Convexity conditions
and
existence theorems
in
non-
linear elusticity,
Arch. Ra.t. Mech. Anal.
63,
1977, 337-403.
[2]
J.
M.
Ball,
Discontinuous equilibrium solutions and cavitation
in
non-linear elasticity,
Phil. Trans.
R.
SOC.
Lond. A306,
1982,
55 7-6 1
1.

Nonlinear Elasticity
467
[3]
J.
M. Ball and D.
G.
Schaeffer,
Bifurcation and stability
of
ho-
mogeneous equilibrium configurations of an elastic body under
dead-load tractions,
Math. Proc. Cambridge Philos. SOC.
94,
1983, 315-339.
[4] M.
F.
Beatty,
Topics in
finite
elasticity: hyperelasticity of rub-
Appl.
bers, elastomers
and
biological tissues-with examples,
Mech. Rev.
40,
1987, 1699-1734.
[5]
M. A. Biot,
Mechaizics of Incremental Defornzutions.
Wiley,
New
York,
19G5.
[6]
P.
G.
Ciarlet,
Mathematical Elasticity
Vol.
I:
Three-dimensional
Elasticity.
North Holland, Ams terd a.m,
1988.
[7] M. A. Dowaikh and
R.
W.
Ogden,
On
srwfcce waves and defor-
mations in
a
pre-stressed incompressible elastic solid,
I. M. A.
J.
Appl. Math.
44,
1990, 261-284.
[8]
R.
Hill,
On uniqueness and stability in
the
theory
of
finite elastic
strain,
J.
Mecli. Phys. Solids
5,
1957, 229-241.
[9] R. Hill,
Aspects
of
invariance in solid mechanics,
Adv. Appl.
Mech.
18,
1978, 1-75.
[lo]
G.
P.
MacSithigh,
Energy-minimal finite deformations of
a
sym-
metrically loaded elastic sheet,
Quart.
J.
Mech. Appl. Math.
39,
1986, 111-123.
[ll]
J.
E.
Marsden and
T.
J.
R.
Hughes,
A4ntlieniaticcl.l Foundations
of Elasticity.
Prentice Hall, Englewood Cliffs, 1983.
[12]
J.
L.
Nowinski,
On the surfuce instability of
(in
isotropic highly
elastic half-space,
Indian
J.
Math. Mech.
18,
190, 1-10.
[13]
J.
L.
Nowinski,
Surface instability of
a
half-space under high two-
dimensional compression,
J.
Fraiikliii Inst.
288,
1969, 367-376.
[14]
R.
W.
Ogden,
Non-linear Elastic Deformations.
Ellis Horwood,
Chichester, 1984.

468
R.
W.
Ogden
[15]
R.
W.
Ogden,
On non-uniqueness in the traction boundary-value
problem for
a
compressible elastic solid,
Quart. Appl. Math.
42,
1984, 337-344.
[16]
R.
W.
Ogden,
Local and global bifurcation phenomena in plane
strain finite elasticity,
Int.
J.
Solids Structures
21,
1985, 121-
132.
[li]
B.
D.
Reddy,
Surface instabilities on
an
equibiazially stretched
hay-space,
Math. Proc. Cambridge Philos. SOC.
91,
1982, 491-
501.
[18]
B.
D.
Reddy,
The occu,rrence of surface instabilities and shear
bands in plane-strain deformation
of
an elastic half-space,
Quart.
J.
Mech. Appl. Math.
36,
1983, 337-3.50.
[19]
R.
S.
Rivlin,
Stability of pure homogeneous deformations of an
elastic cube under dead loading,
Quart. Appl. Math.
32,
1974,
265-271.
[20]
C.
A.
Truesdell and
W.
Noll,
The Nonlinear Field Theories of
IIsndbucli der Physik
Vol.
III/3
(Ed.
S.
Flugge).
Mechanics.
Springer, Berlin,
1965.
[21]
S.
A.
Usmani and M.
F.
Beatty,
On
the surface instability ofa
highly elastic half-space,
J.
Elasticity
4,
1974, 249-263.

Index
A
Acoustic equations
AKNS (Ablowitz, Kaup, Newell,
Segur)
system,
symmetry groups,
41, 42
399
gauge transformations,
343, 344
spectral problem,
321. 322. 343
Algebra, hereditary,
250
Arnold
map,
284
tongue,
288
Attractors,
262
bifurcation,
271
for
equivariant maps,
269
symmetric,
282
B
Ecklund transformation
action of,
328
auto,
324-326
dressing transformation,
324-326
elementary,
326
in
2
+
1
dimensions,
335-340
lattice,
335
nonlinear superposition,
331
BBM equation,
246
Bianchi diagram,
331
Bifurcation
pitchfork,
287, 290
Sacher-Naimark torus,
299
saddle node,
290
Bi-Hamiltonian formulation,
246
Boundary layer equations,
51
symmetry group
for,
51, 52
Boussinesq equation, Riccati type
pseudopotential,
423
Breather,
198
Broomhead-King method,
309
Brusselator,
375, 376, 380
hybrid system,
381
no Riccati type pseudopotential,
415
via Riccati chain,
418
singularity manifold equation,
425-427
Bullough-Dodd equation,
415
Burgers’ equation,
176, 425
C
Canonical transformation, of symmetry group,
Canonical variables,
158-165
Chart,
216
Chaos
159- 16
1
patterned,
259-261
symmetric.
257-313
Cole-Hopf transformation,
176
Computer algebra
for pseudopotentials,
401
for symmetry groups,
66, 67
boundary conditions,
11,
12
nonexistence of solutions,
8-12
weak solutions,
11
Concavity method.
8-12
Conserved quantity, time dependent,
217
Conservation law,
152, 153
gas dynamics,
154
Constant state,
167-171
Constitutive equation,
442
Constraint, incompressibility,
442
Continuous dependence, Holder,
15
Crises,
265
Critical points, hyperbolic,
82
symmetry increasing,
267, 270, 280, 281
D
Davey-Stewartson equation,
193, 336
nonlinear superposition,
338
soliton solutions,
339. 340
469
