Ames W.F., Roger C. Nonlinear equations in the applied sciences. Volume 185
Подождите немного. Документ загружается.


400
M.
C.
Nucci
[38]-[43]
but is not always reliable
[ll].
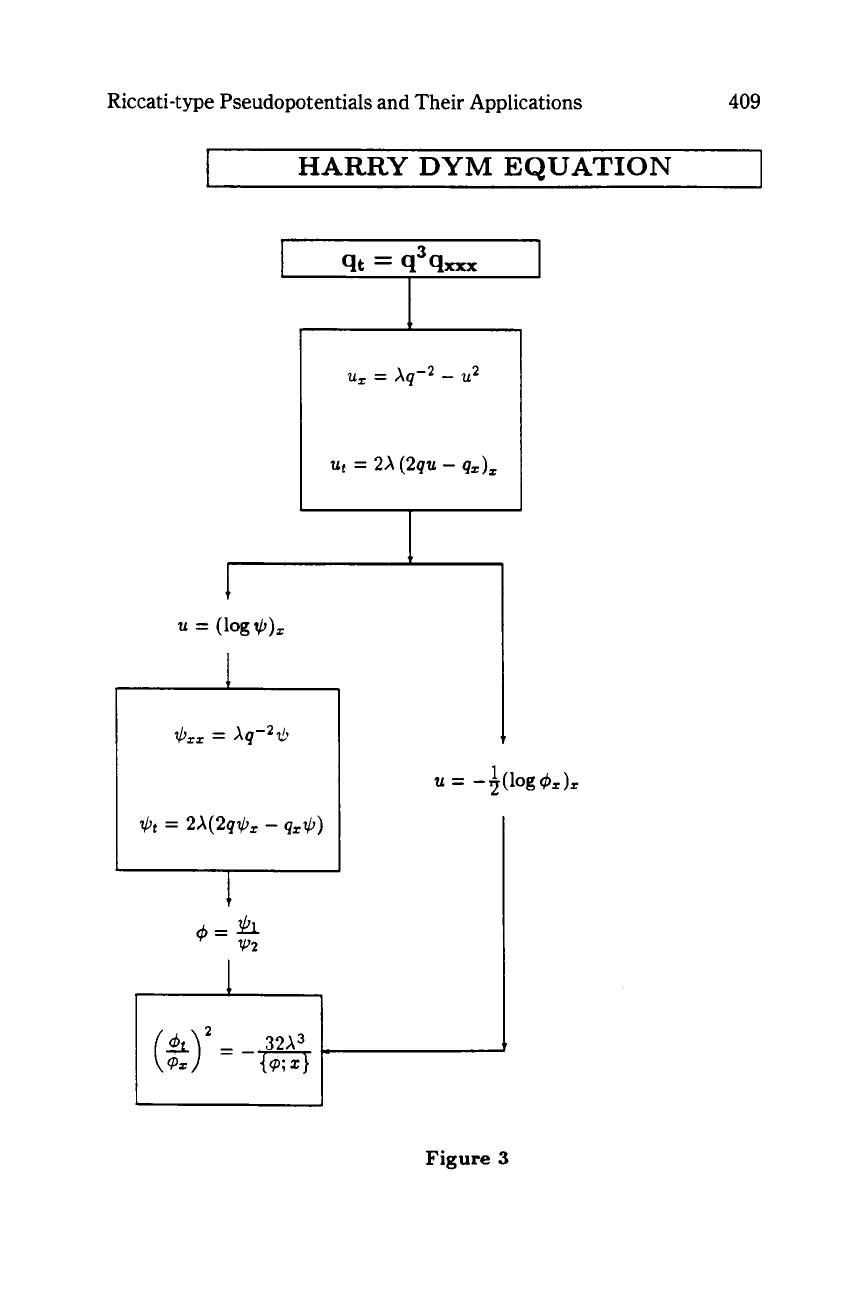
For
example, the Harry Dym
equation does not possess the PainlevC property
[38],
although it is
S-int egrable
[
21.
In
a
fundamental and outstanding paper
[37],
Wahlquist and Es-
tabrook introduced the idea of pseudopotential to the study of NLE
equations in
1+1
dimensions. They used the differential forms ap-
proach to produce pseudopotentials. In particular they obtained the
Lax
equations and the auto-Backlund transformation of the Korteweg-
de Vries equation. Since then many papers have been dedicated to
pseudopotentials. In
[25]
some references are given. Several
au-
thors have found
Lax
equations and auto-Backlund transformations
of NLE equations by using different types of pseudopotentials. It
is known that
a
non-Abelian pseudopotential gives rise to an auto-
Backlund transformation, and
if
it is linear with an arbitrary param-
eter it generates the
Lax
equations
[2].
This monograph is devoted
to
those pseudopotentials which have
defining equations of the Riccati-type
[25]-[30].
This type of pseudopotential generates the
Lax
equations, auto-
Backlund transformation, and singularity manifold equation of the
corresponding NLE equation in
1+
1
dimensions
[25]-[28]
by using
the properties of the Riccati ordinary differential equation.
This technique can be generalized to NLE equations in
2+1
di-
mensions
[27], [28]
by imposing the defining equations of the pseu-
dopotential to be of
a
Riccati-type in one-space variable.
Lax
equations and auto-Backlund transformations for an equa-
tion with higher-order
(2
3)
scattering can also be derived
[30]
if
a
pseudopotential exists such that its defining equations are of
a
type
given by
a
member of the Riccati-chain
[3].
A topic related to Riccati-type pseudopotentials is the derivation
of novel S-integrable equations and their auto-Backlund transforma-
tion from the singularity manifold equations and their invariance un-
der the Mobius group, respectively
[29].
A
well-known example is the
link between the Harry Dym and the singularity manifold equation
of the Korteweg-de Vries equation
[38].
Finally, we consider equations which are not S-integrable. These
equations possess Riccati-type pseudopotentials which derive from

Riccati-type Pseudopotentials and Their Applications
40
1
local conservation laws. The trivial origin of the corresponding
Lax
equations
[8]
annhilates the importance
of
these types of pseudopo-
tentials.
In the following, the direct approach
[13]
is used to search for
pseudopotentials. The extensive calculations involved with this tech-
nique may be greatly simplified by means of
a
Computer Algebra
system. We use ad-hoc interactive REDUCE (version
3.3 [17])
prc+
grams.
2
Riccati-type pseudopotentials
for
NLE
equa-
tions in
1+1
dimensions
2.1
The Riccati equation
The Riccati equation
[MI:
has some interesting properties
[18].
It is related to the linear second
order equation:
V'+)
=
[f:"
-
f&)]
vyz)
-
fo(z)f2(.)V(z)
(2.2)
fd4
if
we set:
1
T(2)
=
--
[log
V(z)l'
f2(4
(2.3)
It is formally invariant under
a
Mobius transformation operating on
the dependent variable
r,
so
that if we assume:
a
+
br*
c
+
dr*
T=-
then
r*
satisfies the Riccati equation:

402
M.
C.
Nucci
where
a,
b,
c,d,
are arbitary constants such that
ad
-
bc
#
0.
Another
property of
(2.1)
is that the cross ratio
of
four
solutions T;
(i
=
1,2,3,4)
of
(2.1)
is
a
constant, i.e.:
If
Vl
and
V2
are two linearly independent solutions
of
the equation:
then:
Vl
w(5)
=
-
v2
satisfies the equation:
{w;x)
=
P+)
-
-
p,”(x)
-
2Po(x)
2
where
{w;
5)
denotes the Schwarzian derivative of
w,
i.e.:
2
{w;x}
=
(2)‘-
-
1
(-)
w”
2
w’
(2.10)
A
remarkable property
of
(2.9)
is its invariance under the
Mobius
group. It is easy to show that the third order differential equation:
{w;
.)
=
WO(4
(k=constant)
(2.11)
is related to the Riccati equation:
T’(5)
=
fo(5)
+
kr2(5)
(2.12)
if
we set:
1
2k
T(5)
=
-[log
w’(z)]’
(2.13)
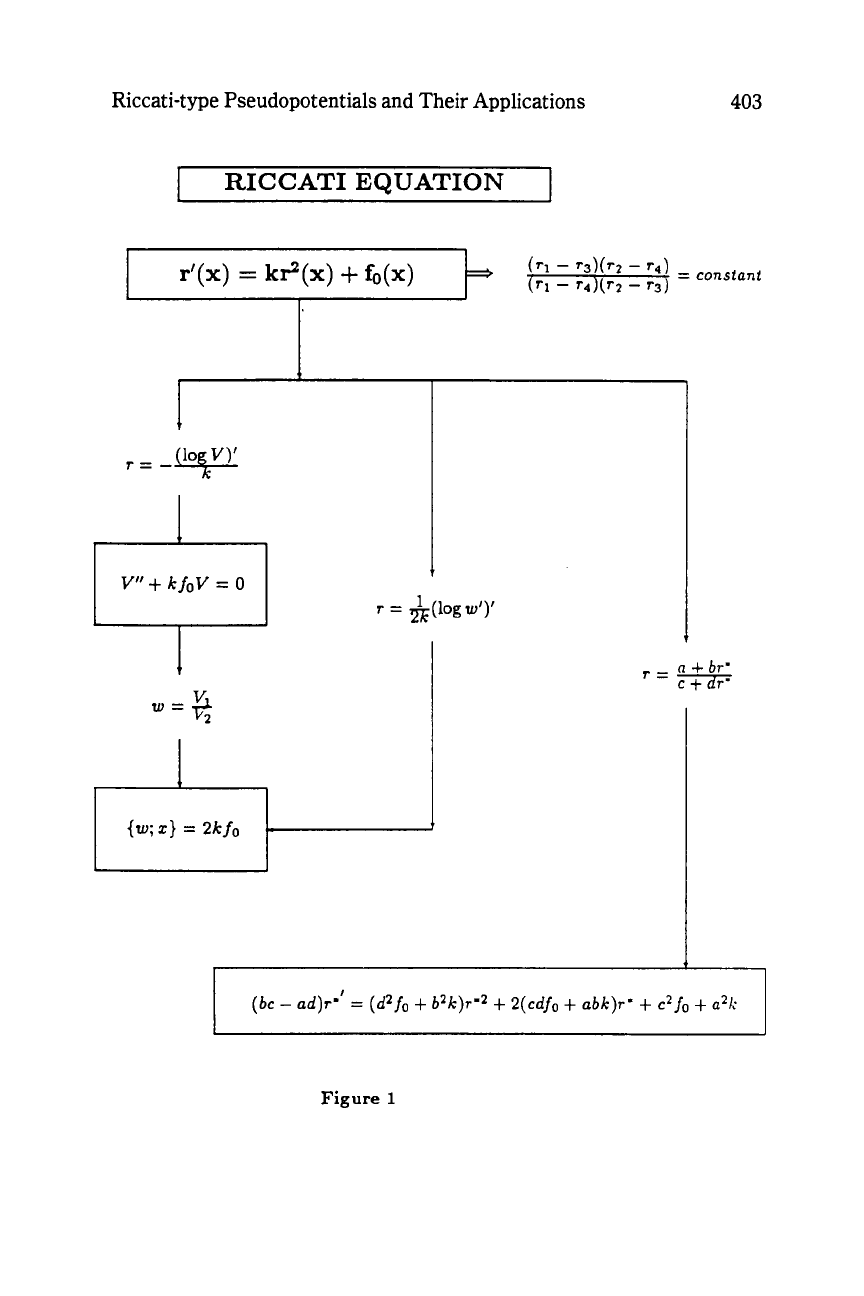
Figure
1
summarizes these properties
for
the Riccati equation
(2.12).
Riccati-type Pseudopotentials and Their Applications
403
I
RICCATIEQUATION
I
w=R
2
{w;
z}
=
2kfo
Figure
1

404
M.
C.
Nucci
2.2
Second-order scattering
Let us consider
a
NLE equation in
1+1
dimensions:
Qt
=
H(q,
Qx,
Qzz,
Qxxx,
*
*
.)
(2.14)
We look for
a
pseudopotential
u
=
u(z,t)
such that:
11,
=
ku2
+
Fi(q)u
+
Fo(q)
(2.15a)
Ut
=
IGl(4,
qz,
* *
.I.
+
Go(%
qz,
* *
"3:
(2.15b)
with the requirement that
uzt
=
utx
whenever (2.14) is satisfied.
If such
a
pseudopotential exists, we obtain the Lax equations from
(2.15) by means
of
(2.16)
1
k
with
?+!J
the spectral function. (2.16) comes from the linearizing trans-
formation (2.3) of the Riccati equation.
If
the equation satisfied by
u,
obtained by eliminating
q
from (2.15), is invariant under the Mobius
21
=
--(log$)z
group, i.e.:
a
+
bu*
c
+
du*
u=-
(2.17)
then, combining:
u;
- -
ku*2
+
Fi(q*)u*
+
Fo(q*)
(2.18)
and (2.15a) through (2.17), we obtain the spatial part of an auto-
Backlund transformation for (2.14), being
q*
another solution of
(2.14). The time part
is
obtained from (2.15b) by
a
similar approach.
In
[5]
the recurrence of the cross ratio property both in Riccati equa-
tions and auto-Backlund transformations was noticed. If there exists
a
pseudopotential
u
such that (2.15a) is given by:
ux
=
ku2
+
Fo(q)
(2.19)
then the singularity manifold equation with dependent variable
4
=
+(z,
t)
is obtained in either two ways. It can be derived from the
Lax
equations by means
of
4=-
$1
$2
(2.20)

Riccati-type Pseudopotentials and Their Applications
405
with
$1
and
$2
two linear independent solutions of the equation sat-
isfied by
+.
(2.20) comes from the transformation (2.8) between the
linear second order equation (2.7) and the third order "Schwarzian"
equation
(2.9).
Also,
the singularity manifold equation can be
ob-
tained from (2.15) by means
of:
1
2k
21
=
-(log
$z)z
(2.21)
(2.21) comes from the transformation (2.13) between the Riccati
equation (2.12) and the third order "Schwarzian" equation (2.11).
It should be noticed that (2.16) and (2.21) imply:
@z
=
$-2
(2.22)
A
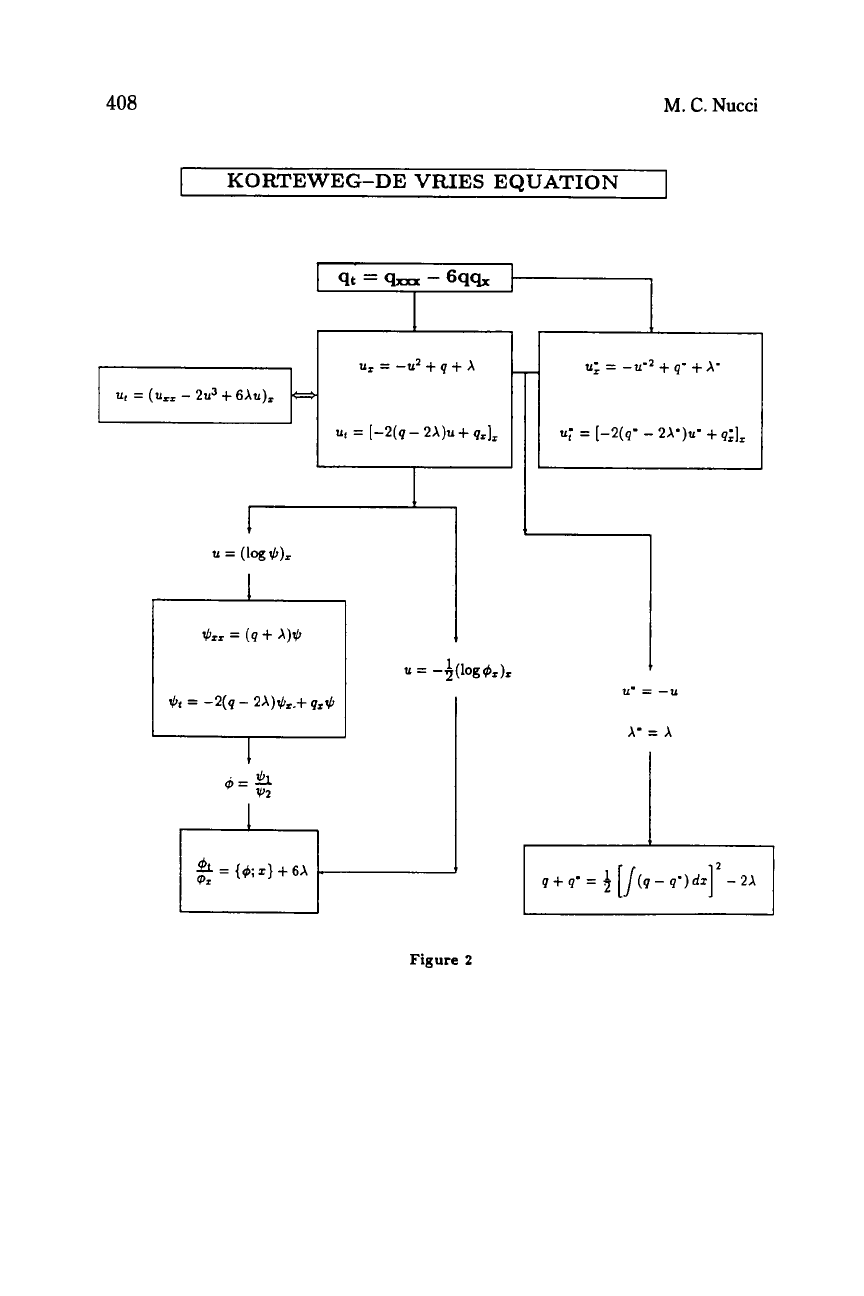
very instructive example
of
this technique is the
Korteweg-de
Vries equation:
Qt
=
Qzzz
-
6qqx
(2.23)
In [28],
a
pseudopotential
u
was found such that:
uz=-u2+q+X (2.24a)
ut
=
[-2(q
-
2+
+
%Iz
(2.24b)
where
X
is an arbitrary constant playing the r81e
of
the spectral
parameter. The
Lax
equations
[lo]:
$22
=
(q+
A)$
(2.25a)
$t
=
-2(q
-
2X)$x
+
qz$
(2.25b)
are easily obtained by applying:
to (2.24). The equation satisfied by
u
is:
ut
=
(uzz
-
2u3
+
6x1~)~
(2.27)

406
M.
C.
Nucci
which is invariant under the transformation:
u*
=
-u
A*
=
x
(2.28)
Then, combining:
u*
X
=
-u*2
+
q*
+
A*
(2.29)
and
(2.24a)
through
(2.28),
we obtain the spatial part of the well-
known auteBBklund transformation for
(2.23),
i.e.:
Q+Q*
=
1
2 [/(q-q*)d2]2-2A
The singularity manifold equation for
(2.23) [38],
i.e.:
(2.30)
(2.31)
is derived by applying either
(2.20)
to the
Lax
equations
or
(2.21)'
to
(2.24).
Figure
2
summarizes these results. Other examples shown
in Figures
3
through
5
include the Harry Dym, sine-Gordon, and
nonlinear Schrodinger equations, respectively.
More examples can
be
found in
[25]-[28].
It should be noticed that the auto-Backlund transformation
of
the Harry Dym equation involves the independent variables
[36].
See
Section
4
for more details.
In
[31],
a
different pseudopotential
u
was found for the sine-
Gordon equation.
It
yields Riccati-type equations with
a
non-constant
coefficient for
u2
and gives rise to the well-known auto-Backlund
transformation of the sine-Gordon equation.
In Figure
5,
the Riccati-type pseudopotential of the nonlinear
Schrodinger equation suggests the following transformation
2:
Q:
Q1
=
-
QC
Q2
=
QQC
(2.32)
which leads to:
Ql,t
=
--+Il,z
+
2q2
+
Q,")z
(2.33a)
'k
=
-1.
2c
x
is
the complex conjugate
of
x.

Riccati-type Pseudopotentials and Their Applications
407
92,t
=
E(q2;c
-
29192)z
(2.33b)
a
conservative form of the nonlinear Schrodinger equation. Note
that the singularity manifold equation is obtained only by means of
(2.20).
408
ut
=
(urr
-
2u3
+
~XU),
M.
C.
Nucci
ee-
KORTEWEG-DE VRIES EQUATION
i
Figure
2
Riccati-type Pseudopotentials and Their Applications
409
I
HARRY DYM
EQUATION
Figure
3
