Ames W.F., Roger C. Nonlinear equations in the applied sciences. Volume 185
Подождите немного. Документ загружается.


330
B.
G.
Konopelchenko
and
C.
Rogers
whence,
and
(3.45)
1'22
2(r21
-
7'0)
=
2r2(p0
-
+
y(Q21
-
qo),
in turn.
On use
of
(3.35)
in
(3.45)
to eliminate
421
we obtain
91
r2
-(m
-
To)
+
2(7'21
-
ro)
+
27'2(X0
-
PO)
=
0,
2
(3.46)
while
(3.36)
yields
91
7-2
-(r12
2
-
TO)
+
2(n2
-
ro)
+
2r2(xO
-
po)
=
0.
(3.47)
Subtraction
of
(3.46)
and
(3.47)
gives
r12
=
7'21
:=
7'3
(3.48)
In
a
similar manner,
(3.44)
together with
(3.35)
-
(3.36)
give
whence, on subtraction,
412
=
421
:=
43
-
(3.51)
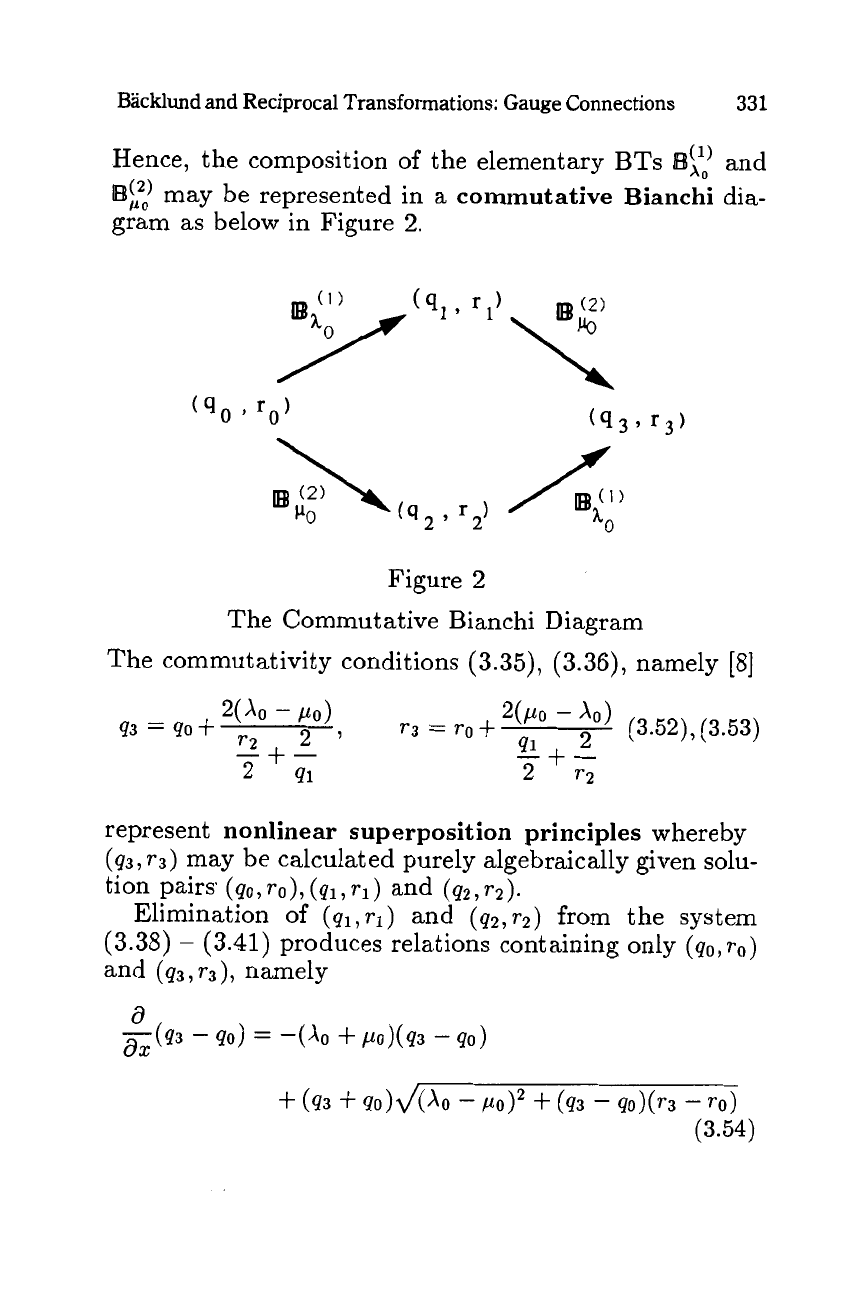
Backlund and Reciprocal Transformations: Gauge Connections
331
Hence, the composition of the elementary BTs and
Br?
may be represented in
a
commutative Bianchi
dia-
gram
as
below in Figure
2.
Figure
2
The Commutative Bianchi Diagram
The commutativity conditions
(3.35), (3.36),
namely
[8]
(3.52), (3.53)
2(Po
-
XO)
41
2
r2
2
’
-+- -+-
2
41
2
7-2
r3
=
7-0
+
2(XO
-
Po)
q3
=
40
+
represent
nonlinear superposition principles
whereby
(43,
r3)
may be calculated purely algebraically given solu-
Elimination
of
(ql,rl)
and
(q2,r2)
from the system
(3.38)
-
(3.41)
produces relations containing only
(qo,
ro)
tion pairs.
(40,
To),
(41,
r1)
and
(42,
r2).
and
(4373),
namely
a
dX
-(43
-
40)
=
-(A0
+
p0)(43
-
40)
+
(43
+
4o)J(Xo
-
po)2
+
(q3
-
qo)(r3
-
(3.54)

332
B.
G.
Konopelchenko
and
C.
Rogers
These relations determine the
(3.55)
simplest non-element ary
In the special
case
r
=
-q,
/Lo
=
-A0
(3.56)
if
we
set
43
:=
q‘,q0
:=
-4
then the well known spatial BT
41
+
Q:
=
(Q
-
Q’)l/4G-
I
Q
+
Q’
l2
(3.57)
for the
NLS
(3.5)
is retrieved
[l].
The existence
of
nonlinear superposition principles un-
derlying auto
BTs
is
of
the greatest importance since it
allows
us
to generate, by iteration
of
purely algebraic
procedures, sequences
of
exact solutions to the nonlinear
evolution equations amenable to the inverse scattering
method. In particular, multi-soliton solutions may be
so-generat ed.
Here, the procedure is illustrated for the coupled
NLS
system
(3.4).
This admits the starting trivial solution
P=Po,o:=
(;
;),
(3.58)
corresponding to
(4,
T)
=
(40,
TO)
=
(0,O).
Substitution
in the Backlund relations
(3.38)
and
(3.40)
with
A0
-+
XI,
/LO
+
yields,
on
application of
By:
and
Bz)
to
(40
,
To)
841
-
+
2AlQl
=
0,
dX
7-1
=
0,

Backlund and Reciprocal Transformations: Gauge Connections
333
whence
2x12
41
=
d(t)e-
,
r1
=
0
Qz
=
0,
r2
=
$(t)
e2cL12.
The nature of
d(t)
and
+(t)
may be determined by the
temporal part
of
the
BT.
Alternatively, on substitution
back in the original
NLS
system
(3.4)
we
obtain
4ix~t-2X1(2-201)
Q1
=
Q(l0)
=
e
7
r1
=
r(10)
=
0,
-4ip;t+2pi
(Z-?oi)
Q2
=
Q(0l)
=
0,
7.2
=
T(01)
=
e
where
xol,
Fol
are arbitrary constants.
now yields.
Application
of
the nonlinear superposit ion principle
2(p1
-
A,)
Ql,O
2
*
2
r0,1
7-3
=
By!Bj,2!ro
:=
r1,1
=
r0,o
+
-+-
On repeated application
of
the elementary BTs to
Po
we
obtain
where the nonlinear superposition principle yields

334
B.
G.
Konopelchenko
and
C.
Rogers
(3.61)
2(p1
-
A,>
rnl+l,nz+l
=
rn1
,nz
+
2’
+
Qnl+l,nz
2
rn,
,nz+l
n1,n2=0,1
,....
The
solutions
Pnl,o
and
Po,nz
are
readily derived
via
the
Backlund relations and are given by
721
qn1,O
=
Ce
7
rn1,O
-0
-
(3.62)
42xi
1-2xk
(d-dok)
k=
1
k=
1
where
Xok
and
ZOk
are arbitrary constants. The remaining
solutions
Pnl,nz
may now all be calculated by
a
purely
algebraic procedure on use
of
the nonlinear superposition
principles
(3.60)
-
(3.61).
Thus, in particular, on use
of
Po,O,Pl,o
and
P0,l
it
is
seen that
(3.65)
Further, on application
of
(3.60)
-
(3.61)
to
Po,l,
Pl,I,Po,2
we obtain
P1,2.
Iteration
of
this procedure leads to any
Pn1
,nz
[8].
This is given in terms
of
q1,O
...qn!,?
and
TO,^
. . .
,
~0,~~.
Thus,
Pnl
,nz
is
a
nonlinear
superposltlon
of
plane wave solutions
to
the decoupled
linear
Schrodinger equations
iqt
+
Qzz
=
0,
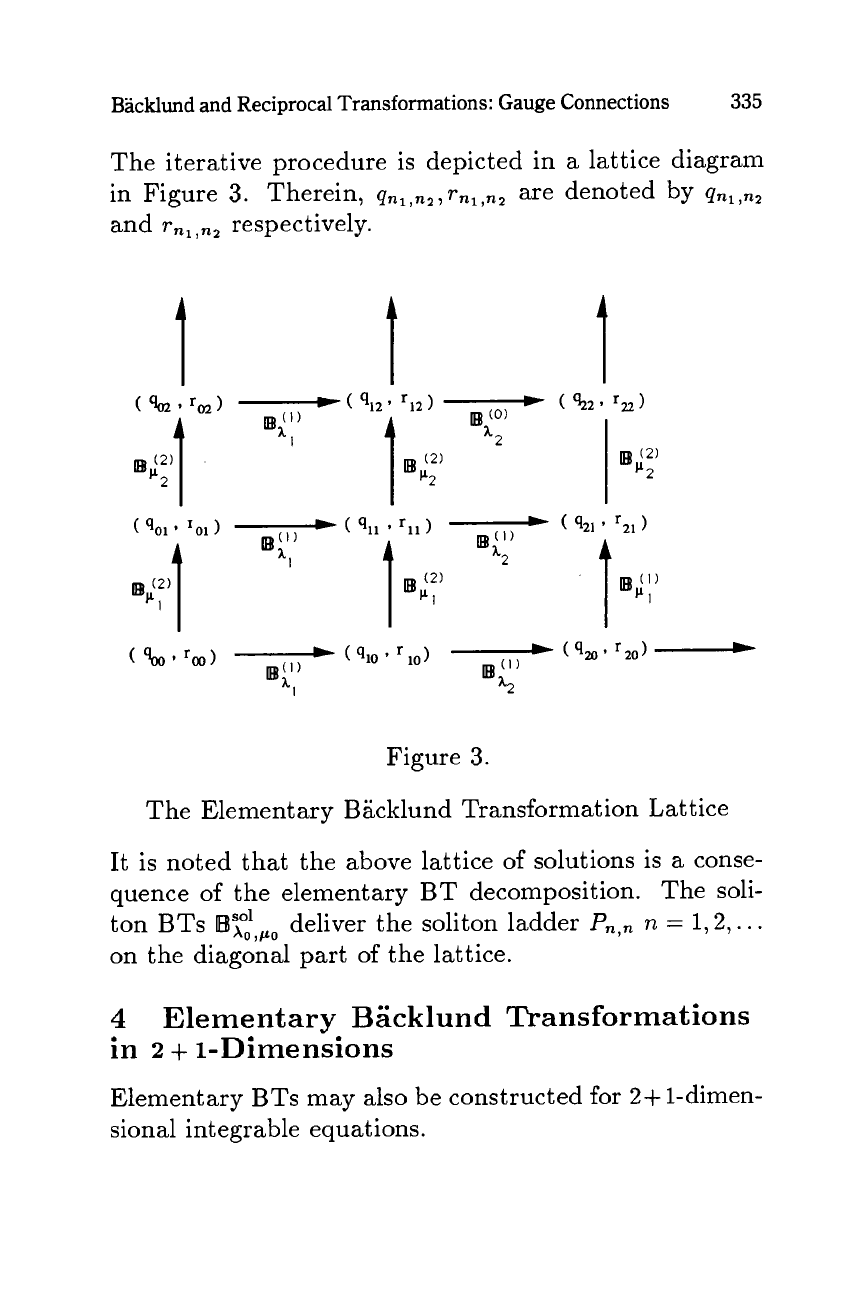
Backlund and Reciprocal Transformations: Gauge Connections
335
The iterative procedure is depicted in
a
lattice diagram
in Figure
3.
Therein,
qnl,nz,rnl,nz
are denoted by
qnl,nz
and
rnl,nz
respectively.
I
L
Figure
3.
The Elementary Backlund Transformation Lattice
It
is noted that the above lattice of solutions is
a
conse-
quence of the elementary
BT
decomposition. The soli-
ton BTs
deliver the soliton ladder
Pn,n
n
=
1,2,.
. .
on the diagonal part
of
the lattice.
4
Elementary Backlund Transformations
in
2
+
1-Dimensions
Elementary BTs may also be constructed for
2+
l-dimen-
sional integrable equations.

336
B.
G.
Konopelchenko
and
C.
Rogers
In the
2+
1-dimensional generalization of the
ZS-AKNS
system we are concerned with the pair
of
linear equations
where
d
d
3Y
Tl
=
+
c3-
+
P(x, y,
t)
at
(4.3)
with
(4.4)
0
!l(X,Y,t)
P=
(
r(x,
Y,
t>
0
The compatibility condition
[Tl,
7-21
=
0
(4.6)
with
various
V
x,
y,
t,
generates
2
+
1-dimensional in-
tegrable nonlinear systems for
q,
r.
In particular, corre-
sponding to
0
we obtain
a
2
+
I-dimensional integrable generalisation
of
the system
(3.4),
namely the Davey-Stewartson
(DS)
system

Backlund and Reciprocal Transformations: Gauge Connections
337
where
4
is an auxiliary
2
x
2
diagonal matrix
[2].
The
DS
system was first derived in the analysis
of
the propagation
of two-dimensional nonlinear waves in dispersive media
The dressing method may be extended to integrable
systems in
2
+
1-dimensions
[2].
In this case, the dress-
ing (gauge) operator
G
adopts
a
polynomial
form in the
derivative
-,
namely
[I11
PI.
d
dY
The elementary dressings
G(l)
and
G(2)
may be shown
to
be given by
where
(4.11)

338
B.
G.
Konopelchenko
and
C.
Rogers
The spatial parts of the corresponding elementary
BTs
are given by
where
-1
-1
8;'
:=
(g
+
g)
8;
1
:=
(L
-
6)
.
(4.14)
Nonlinear superposition principles which generalize
(3.52), (3.53),
namely
with
I3iicklund and Reciprocal Transformations: Gauge Connections
339
are readily derived. The associated commutative Bianchi
diagram allows the construction
of
a
lattice
of
exact
so-
lutions to the
DS
system
(4.8).
The solutions
Pnl,o
and
Po,n2
which generalize
(3.62),
(3.63)
are given by
Qn1,O
=
2
J,
~ik)(P)*
k=l
exp (22
-
p2)
t
+
p(z
+
y)
-
Ar)(x
-
y)}
dp
rn1,o
=
0,
~0,n2
=
0,
(4.18)
I
(4.19)
where
Cik)(p),
Cik’(v)
are arbitrary functions and
rl,
r2
are arbitrary contours in the complex planes of the vari-
ables
p
and
v.
The simplest soliton-type solution
Pl,l
of the
DS
equa-
tion is of the form
n2
r0,nz
=
c
J,
~i~’(u>.
k=l
7.
I
exp
{
22
-
u2)
t
-
v(x
+
y)
+
Ar)(x
+
y)}
du
1
Ql,l
=
-
(A1
+P)Cl(P).
ZJ
J,,
exP{qA;
-
P2)t
+
P(2
+
y)
-
h(a:
-
y)}&
(4.20)
exp{2i(Xi
-
v2)t
-
v(a:
-
y)
+
A2(z
+
y)}dv
