Ames W.F., Roger C. Nonlinear equations in the applied sciences. Volume 185
Подождите немного. Документ загружается.


290
Greg
King
and
Ian
Stewart
Figure 16:
A
saddle-node bifurcation in
a
circle map.
Figure 17: Pitchfork bifurcation.
dynamics, exactly
as
for the one-humped map. The symbolic dy-
namics tracks the itinerary of the critical point of the one-humped
map, leading to the concept of
a
kneading
sequence.
The symmetries
can be inserted into the symbolic dynamics to provide
a
rigorous
check on how much symmetry exists within the window.
It
is con-
jectured that there always exist subwindows in which
all
possible
broken symmetries occur.
Similar ideas apply
to
pitchfork bifurcations, where again we can
find invariant intervals
for
fQ,
as
in Figure
17.
Now, however, the be-
haviour within the parameter window is controlled by
a
two-humped
map with
22
symmetry; that is, it follows the model of the cubic
logistic map, with period-doubling cascades, chaos, and
a
symmetry-
increasing crisis. The crisis occurs at the stage
of
Figure 17(d), when
the humps poke out
of
their confining boxes. Provided the humps
remain within the outer box,
a
symmetry-increasing crisis occurs.

Symmetric
Chaos
291
Figure
18:
Circuit for
a
Van der Pol-Duffing Oscillator.
Considerations
of
this kind explain the majority
of
features ac-
tually observed in numerical experiments with the Arnold maps:
see
Krupa and Roberts
[25]
for details. Clearly there are many additional
questions yet to be tackled.
7
Electronic Circuits
What connection do these theoretical ideas have with experiments?
Can symmetric chaos be observed in ther laboratory? One area
in which
a
number
of
experiments on symmetric chaos have been
done is electronic circuits. We report here on some
of
this work:
the systems discussed are
a
Van der Pol-Duffing Oscillator,
a
Van
der Pol-Duffing Oscillator with quintic characteristic, and coupled
identical oscillators. They are modelled by continuous dynamical
systems, and studied by means of equivariant Poincarb maps.
7.1
Van
der
Pol-Duffing
Oscillator
The circuit for
a
Van der Pol-Duffing Oscillator is shown in Figure
18.
It
consists of an RC-oscillator resistively coupled to
an
LC oscillator.
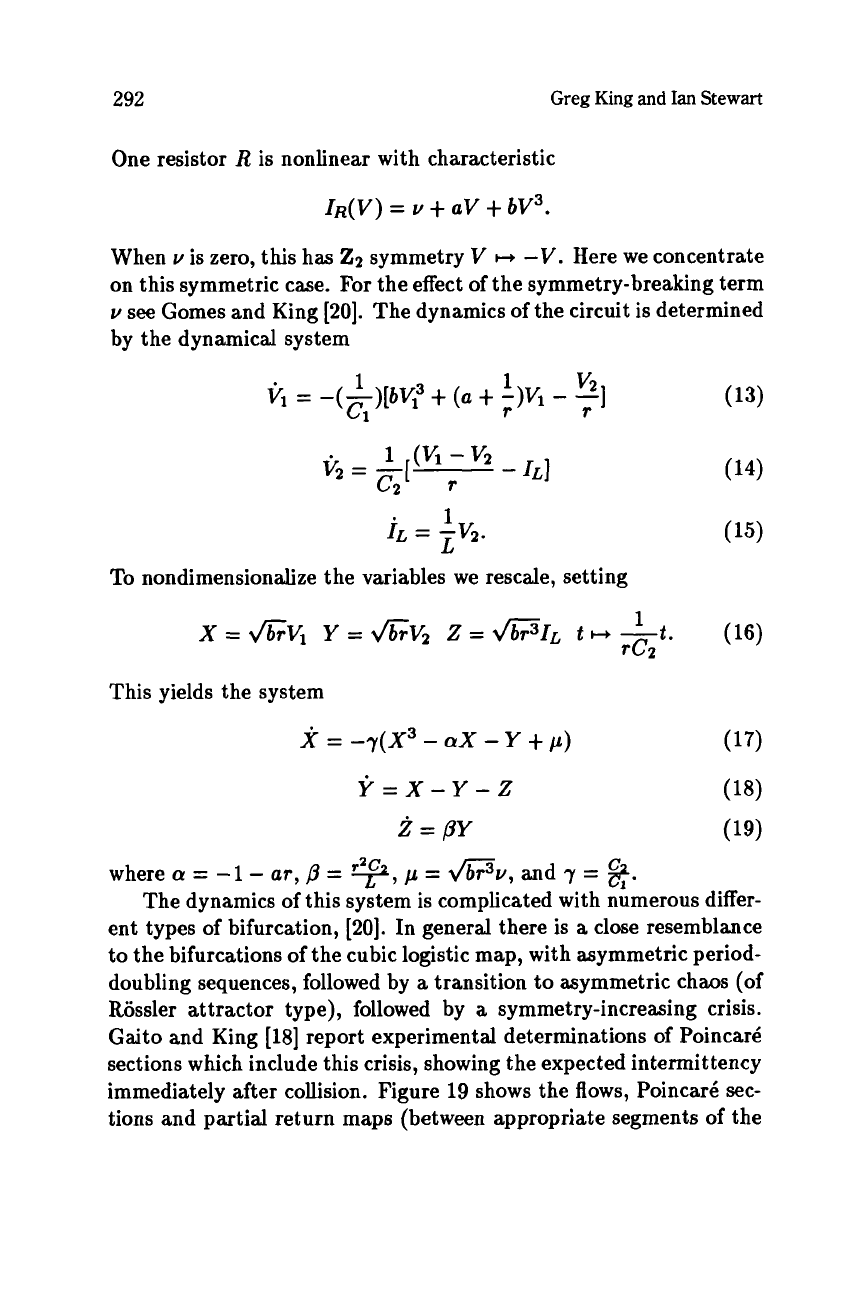
292
Greg
King
and
Ian
Stewart
One resistor
R
is nonlinear with characteristic
IR(V)
=
u
+
aV
+
bV3.
When
u
is zero, this has
Z2
symmetry
V
H
-V.
Here we concentrate
on this symmetric case.
For
the effect of the symmetry-breaking term
u
see
Gomes and King
[20].
The dynamics of the circuit is determined
by the dynamical system
1 1
vz
+I
=
-(-)[bV,3
+
(a
+
;)Vl
-
-1
7-
Cl
-1
IL
=
-V2.
L
To nondimensionalize the variables we rescale, setting
(15)
This yields the system
x
=
-y(X3
-
ax
-
Y
+
p)
(17)
Y=x-Y-z
i=pY
2C
where
a
=
-1
-
ar,
p
=
y,
p
=
mu,
and
y
=
2.
The dynamics of this system is complicated with numerous differ-
ent types of bifurcation,
[20].
In general there is
a
close resemblance
to the bifurcations
of
the cubic logistic map, with asymmetric period-
doubling sequences, followed by
a
transition to asymmetric chaos (of
Rossler attractor type), followed by
a
symmetry-increasing crisis.
Gaito and King
[18]
report experimental determinations of Poincard
sections which include this crisis, showing the expected intermittency
immediately after collision. Figure
19
shows the flows, Poincard sec-
tions and partial return maps (between appropriate segments of the

Symmetric
Chaos
293
Poincar6 section) in the
two
cases. The Poincarh sections are essen-
tially 1-dimensional (though what appear
to
be curves presumably
have the usual thin Cantor set cross-sectional structure, which we
ignore). They involve several distinct ‘curves’, and it is
a
nontriv-
ial matter to select the appropriate segments of the set
for
drawing
return maps.
Observe that the return map has the expected
22
symmetry,
with the group acting
as
rotation through
I,
and that the crisis
oc-
curs when the peaks in the mapping break through the zero level,
permitting the state
of
the system to escape from the positive
or
negative interval and explore the entire line. This is similar
to
the
behaviour of the cubic logistic map. The analogy can to some extent
be explained by transposing the left and right halves
of
the interval
(-T,
T)
in Figure 19(c,d), after which transformation the Poincar6
map qualitatively resembles
a
cubic curve. However, this is
a
discon-
tinuous transformation which introduces some (not insoluble) inter-
pretational problems.
The complete dynamics is complicated.
It
can be visualised using
a
knot-holder,
a
concept introduced
-
though not under that name
-
by Birman and Williams
[3],
which effectively represents the thin
but intricately layered structure
of
the attractor
as
a
surface. This
takes the form
of
Figure
20.
It can also be modelled in terms of a
fast/slow decomposition of the vector field, in which the phase point
makes chaotic transitions between two layers of
a
3-sheeted surface,
or
alternatively between two adjacent potential wells. The spiral
motion that occurs
as
the point jumps from one sheet to the other
is responsible for some of the structure in the Poincar6 sections, and
we must restrict attention to suitable subsets,
as
mentioned above.
7.2
Castro
[S]
has extended some of this work to an oscillator with
a
quintic characteristic
Quintic Van
der
Pol-Duffing Oscillator
IR(V)
=
u
+
av
+
bV3
+
cv5,
which can be thought of
as
modelling
a
particle moving in
a
sym-
metric system of three adjacent potential wells. Two experimentally

294
2.5
lo4
c3
-2.5
lo4
n
f1ip.C
-8.0
104
8.0
lo4
C1
-2.5
104
-1
-8.0
lo4
8.0
104
XI
fliD.0
-n
0"
m
Greg
King
and
Ian
Stewart
-2.5
lo4
a
-8.0
lo4
8.0
lo4
C1
-2.5
lo4
a
8.0
lo4
x,
-8.0
lo4
flio.
Ob
1
-n
en
Figure
19:
Experimentally determined
flow,
Poincarh section, and
partial return map for the
Van
der Pol-Duffing oscillator. Left: sym-
metric case
Y
=
0.
Right: asymmetric case
Y
#
0.

Symmetric
Chaos
295
D+
I
/
+fold
line
Figure
20:
Knotholder for the fully symmetric strange attractor
of
the Van der Pol-Duffing oscillator.

296
Greg
King
and
Ian
Stewart
determined Poincar6 sections
are
shown in Figure 21. These figures
in many ways resemble an €-lift
of
a
quintic analogue
of
the logistic
map, but with
c
quite large, taking the form
(;)
(
rytAx+Bx3+Cx5
X
See Figure 22.
This resemblance is related
to
a
fast/slow decomposition
of
the
dynamics which corresponds to
a
physical picture of the oscillator
as
a
particle moving either in the central well
or
in
all
three. See
[8]
for
more details.
7.3
Coupled Identical Oscillators
Richer symmetries than
22
occur in systems of
n
symmetrically cou-
pled oscillators. Ashwin, King, and Swift [2] study systems
of
this
type having symmetry group
S,,
the symmetric group
of
degree
n.
The symmetries
are
induced by permutations of the oscillators.
In particular they focus on the case
n
=
3.
The cited paper con-
cerns non-chaotic dynamics, which can be reduced to
a
S3-
equiv-
ariant dynamical system on
a
2-torus. They predict
a
new type
of
codimension-
1
bifurcation, and find it experimentally in
a
network
of
coupled Van der
Pol
oscillators.
Ashwin
[l]
develops these ideas further, and studies chaos in such
systems when
n
=
3
or
4. He uses the circuit of Figure 23, which
is
a
system of coupled identical Van der Pol oscillators forced by
a
sinusoidal signal. The results are plotted by assigning one of
n
unit vectors, arranged in the plane at angles of
%,
to the voltage
in each oscillator, and plotting
a
Poincard section synchronised with
the times at which the forcing signal generator passes through zero
from negative to positive. This is
a
D,-equivariant projection
of
the voltage data, in the sense of section 8.2 below. Because it is
a
projection, the images of attractors may appear to overlap.
We describe two particular bifurcation sequences observed in
these experiments. Both begin with
a
Zs-symmetric 2-torus
(a).
In the first, Figure 24, this symmetry-locks (b) to
a
3:2 resonance,

Symmetric
Chaos
-
..'.
.
..
.
.
.
. . . .
.
.;
-. . .
.:.
.
.
.
.
.
. .
.
.
.1..
.
,
,
.:
I(
;!
\,
1'
:
-..
..
*.I..
.
;.'
297
7.0
lo4
7
-7.0
lo4
1.2
lo5
'5
-1.2
105
3.5
104
7
-3.5
lo4
i
7.0
104
5
-7.0
lo4
7.0
lo4
3.5
lo4
c2
c2
-7.0
lo4
-3.5
104
1.2
105
-7.0
104
7.0
104
Figure
21:
Experimental flows (above) and Poincark sections (below)
for
the quintic Van der Pol-Duffing oscillator. (a) Confined to the
central well. (b) Moving in
all
three wells.
298
Greg King
and
Ian
Stewart
Figure 22: Attractor in a lift
(20)
of a quintic logistic map.
operational
amplifier:
symbolize as
from
signal
generator
Figure 23: System
of
three
or
four forced coupled identical oscillators.

Symmetric
Chaos
299
which period-doubles to
a
6:4
resonance (c) and then undergoes
a
Sacher-Naimark torus bifurcation (d) to
a
2-torus at
6:4
resonance.
In (e) the 2-torus becomes
a
chaotic attractor with
Z3
symmetry. By
(f) there has been
a
symmetry- increasing crisis to
S3
symmetry.
In the second, Figure
25,
the initial bifurcation (b) is
a
Sacher-
Naimark torus bifurcation to
a
3-torus. The amplitude of the
3-
torus increases, and we
see
(c)
a
bunching of trajectories where it is
conjectured to approach
a
hyperbolic 2-torus. By (d) the two tori
have collided in
a
heteroclinic bifurcation, destroying the 3-torus.
In (e) the attractor has become chaotic with
23
symmetry. By (f)
there has been
a
symmetry-increasing crisis to
S3
symmetry. There
is some resemblance to Figure llb.
8
Time Series Analysis
The detection of chaos from time series is
a
widely studied problem,
and the basic principles are now becoming fairly well understood,
at least for data from well-controlled experiments. Many different
techniques have been devised. The first goes back to Packard [28]
and Takens [34]. More recent improvements have been obtained in
particular by Broomhead and King
[6]
for flows, and Broomhead and
King [7] for mappings.
However, the detection of symmetric chaos requires further refine-
ments if we wish to find out what the symmetries of the attractor
are. For example, if we take one of Chossat, Field and Golubit-
sky’s
D3
attractors and plot its
x-
and y-coordinates
as
two separate
time series, then the symmetry is by no means apparent (Figure
26).
This is not especially surprising, since the
x-
and y-coordinates are
not related in
a
symmetric fashion. If instead we plot (Figure 27)
time- series
for
the variables
x,
x/2
+
fiy/2,
x/2
-
ay/2, which
are permuted by
D3,
we observe something rather more interesting.
First, of course, the three time series in Figure 27(a), say, are not
identical.
If
they were, it would mean that every individual point on
the attractor, rather than just the attractor itself, would have
D3
symmetry,
so
the attractor would be just the origin. What we see,
however, is that all three time series have
a
very similar appearance.
