Ames W.F., Roger C. Nonlinear equations in the applied sciences. Volume 185
Подождите немного. Документ загружается.

270
Greg
King
and
Ian
Stewart
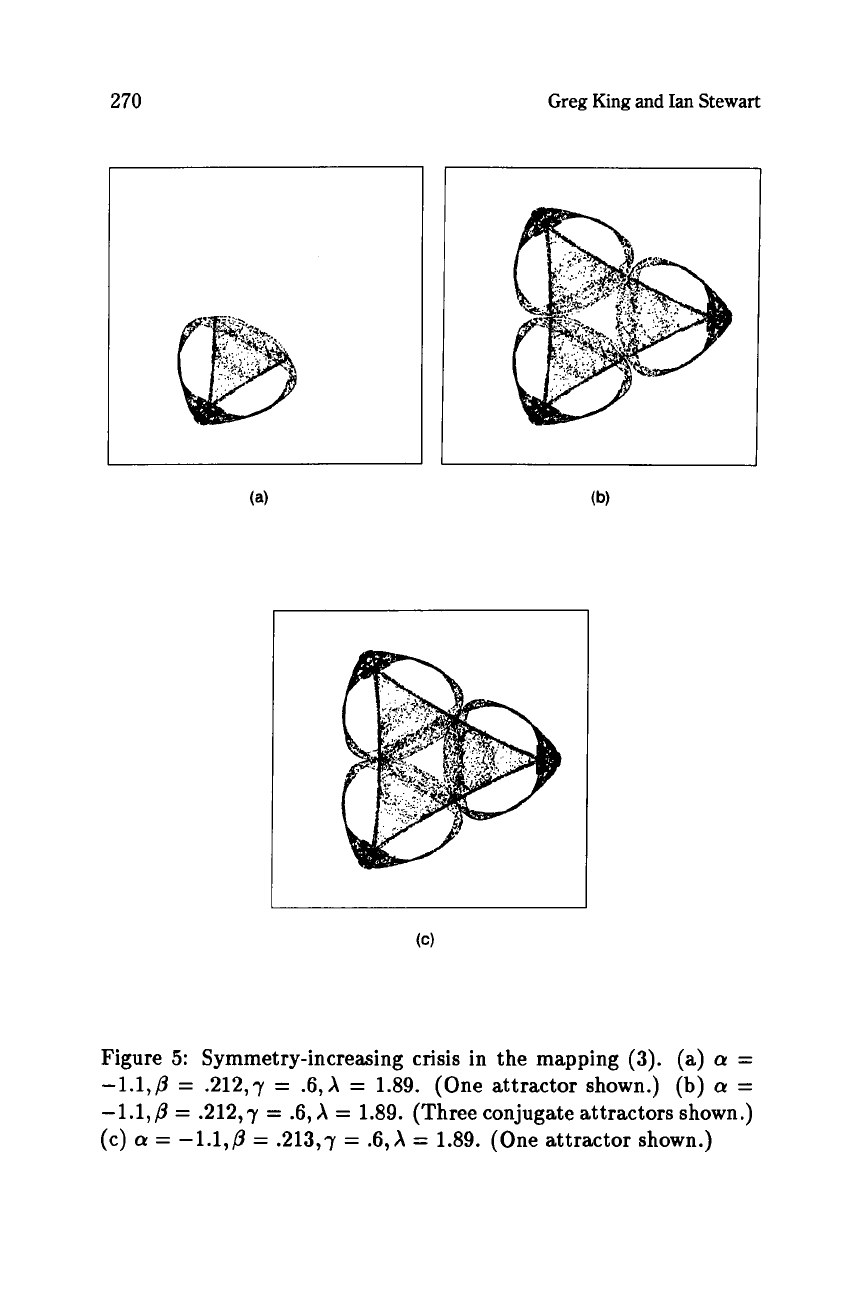
Figure
5:
Symmetry-increasing crisis in the mapping
(3).
(a)
a
=
-1.1,p
=
.212,7
=
.6,X
=
1.89.
(One attractor shown.)
(b)
a
=
-1.1,p
=
.212,7
=
.6,
X
=
1.89.
(Three
conjugate attractors shown.)
(c)
a
=
-1.1,p
=
.213,7
=
.6,X
=
1.89.
(One attractor shown.)
Symmetric
Chaos
271
.I
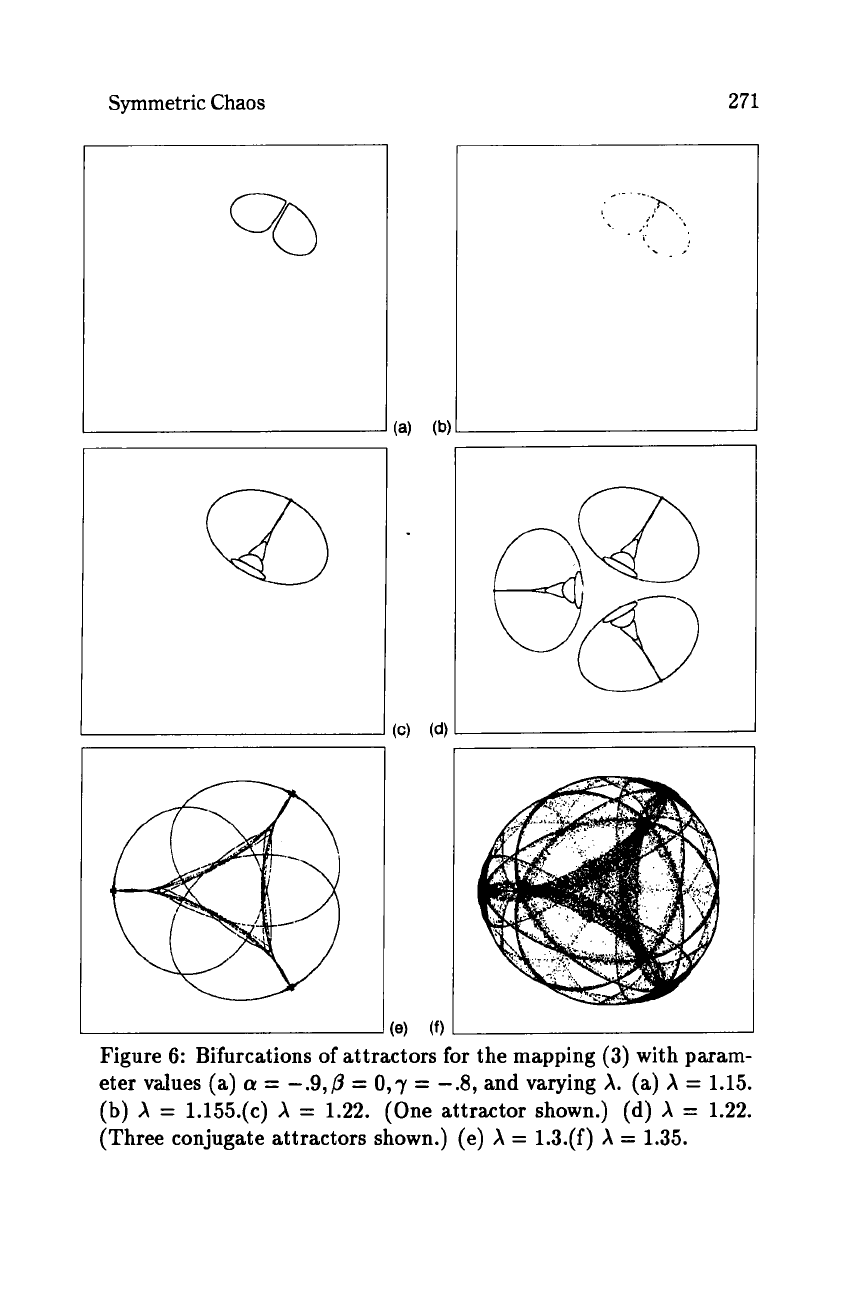
Figure 6: Bifurcations of attractors for the mapping (3) with param-
eter values
(a)
a
=
-.9,p
=
O,7
=
-.8,
and varying
A.
(a)
X
=
1.15.
(b)
X
=
1.155.(c)
X
=
1.22. (One attractor shown.) (d)
X
=
1.22.
(Three conjugate attractors shown.) (e)
X
=
1.3.(f)
X
=
1.35.
272
Greg
King
and
Ian
Stewart
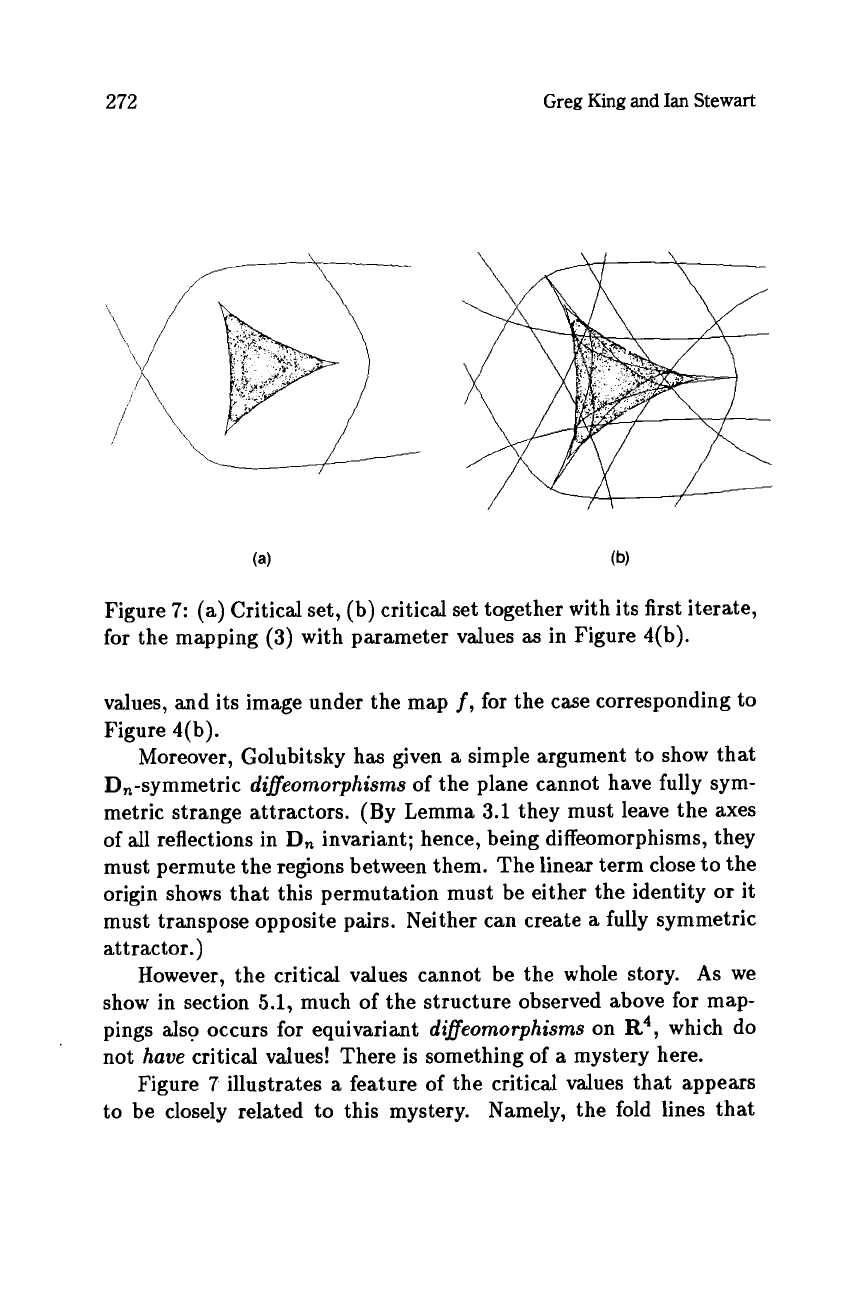
Figure
7:
(a) Critical set, (b) critical set together with its first iterate,
for the mapping
(3)
with parameter values
as
in Figure 4(b).
values, and its image under the map
f,
for the case corresponding to
Figure 4(b).
Moreover, Golubitsky has given
a
simple argument to show that
D,-symmetric
difleomorphisms
of the plane cannot have fully sym-
metric strange attractors. (By Lemma
3.1
they must leave the axes
of
all
reflections in
D,
invariant; hence, being diffeomorphisms, they
must permute the regions between them. The linear term close to the
origin shows that this permutation must be either the identity
or
it
must transpose opposite pairs. Neither can create
a
fully symmetric
attractor.)
However, the critical values cannot be the whole story.
As
we
show in section
5.1,
much of the structure observed above for map-
pings also occurs
for
equivariant
difleomorphisms
on
R4,
which do
not
have
critical values! There is something of
a
mystery here.
Figure
7
illustrates
a
feature of the critical values that appears
to be closely related to this mystery. Namely, the fold lines that

Symmetric
Chaos
273
determine the critical values can form trapping regions, confining the
dynamics. (Observe how the cusped triangle is folded up and laid
down within itself.) If no stable regular dynamics is possible within
such
a
region, then
a
strange attractor must be present; moreover,
it is likely to encounter the fold lines along parts of the edge
of
that
region.
So
critical values provide
a
plausible mechanisms
for
the
formation of attractors, especially strange attractors.
For
mappings in the plane it often seems
to
be the case that the
critical
set,
or
its first
or
second iterate, lie very close to any attractors
that occur. One question that this raises
is
the following: when can
we obtain the attractor by iterating the critical set? Clearly this
cannot happen for diffeomorphisms; but the numerical evidence is
that it happens for
a
very broad class of maps.
4.3
Torus
Maps
This section describes preliminary stages
of
some joint work with
Golubitsky, which was stimulated by
a
morning television programme
in Minneapolis on computer design
of
textiles. An especially rich
source of symmetric strange attractors arises from equivariant torus
maps
f
:
T2
-,
T2
where
T2
is the 2-torus. Here we discuss the
D
4
-equi var i
an
t
family
of
maps
(A
+
a
cos(2sy)) sin(2nz)
+
psin(4rz)
+
rsin(6rz)
cos(4ny)
+
Az
(A
+
a
cos(27rc)) sin(2ny)
+
psin(4sy)
+
7
sin(6sy)
cos(4rz)
+
Ay
(4)
where
a,
P,7,
A
are red
parameters and
k
is
an
integer parameter.
The form of this mapping is deduced from
a
Fourier expansion, to-
gether with linear terms, by applying the generators of the symmetry
group
D4
of the unit square defining
a
fundamental domain for the
torus. Only ‘low order’ terms of the Fourier series are retained here.
We content ourselves with some examples revealing the extraor-
dinary richness of these maps.
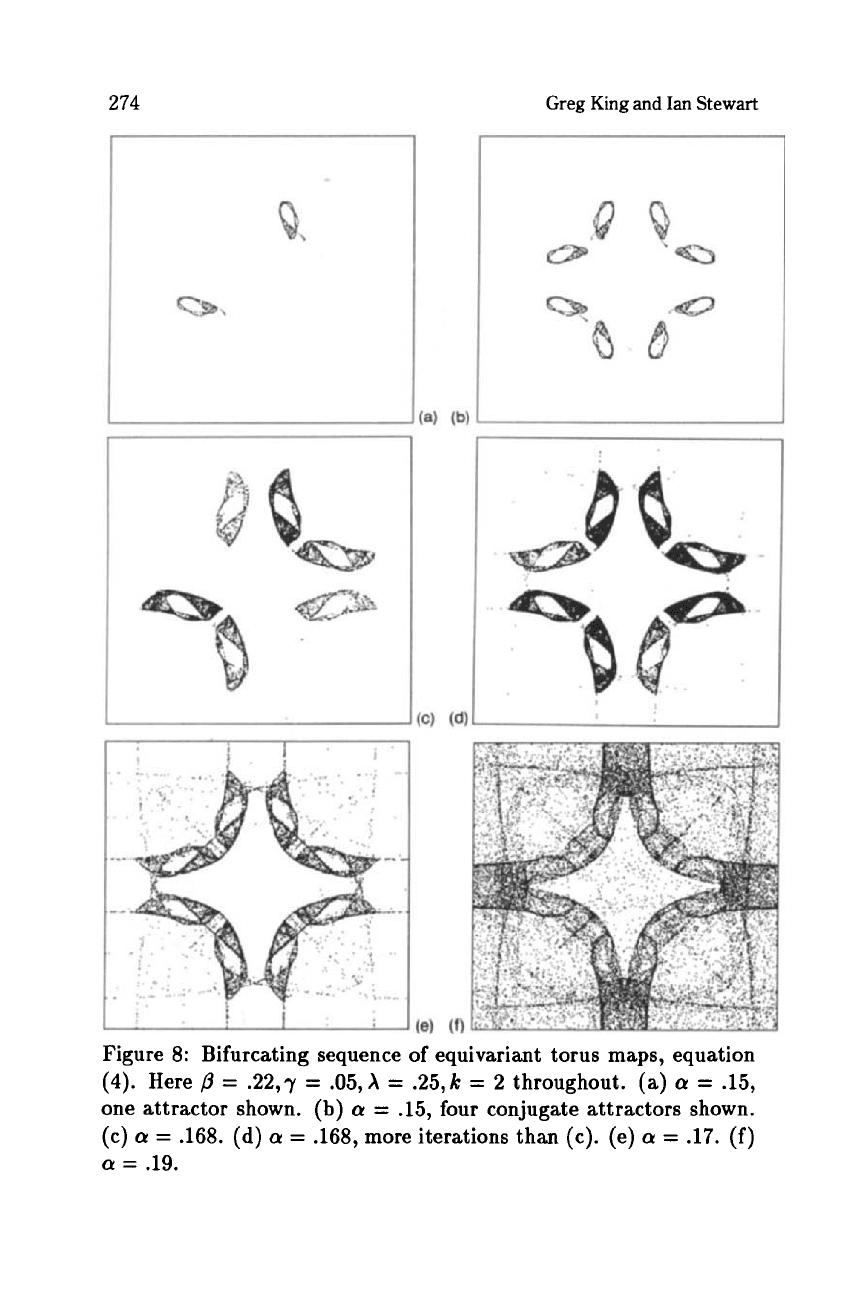
The sequence in Figure
8
illustrates
a
symmetry-increasing crisis.
In (a) we
see
one attractor, symmetric about
a
diagonal. In (b) we
see
its four conjugates. In (c) not all of the attractor has yet appeared,
because
of
intermittency. The figure shows three pairs of
sets,
each
274
Greg
King
and
Ian
Stewart
Figure 8: Bifurcating sequence of equivariant torus maps, equation
(4).
Here
/3
=
.22,7
=
.05,
X
=
.25,
k
=
2
throughout. (a)
a
=
.15,
one attractor shown.
(b)
cy
=
.15,
four conjugate attractors shown.
(c)
a
=
.168.
(d)
a
=
.168, more iterations than (c). (e)
a
=
.17.
(f)
a
=
.19.
Symmetric
Chaos
275
i:.
. .
1
:
.
,.
.,
.
-.
...
.
....
...,
,
.
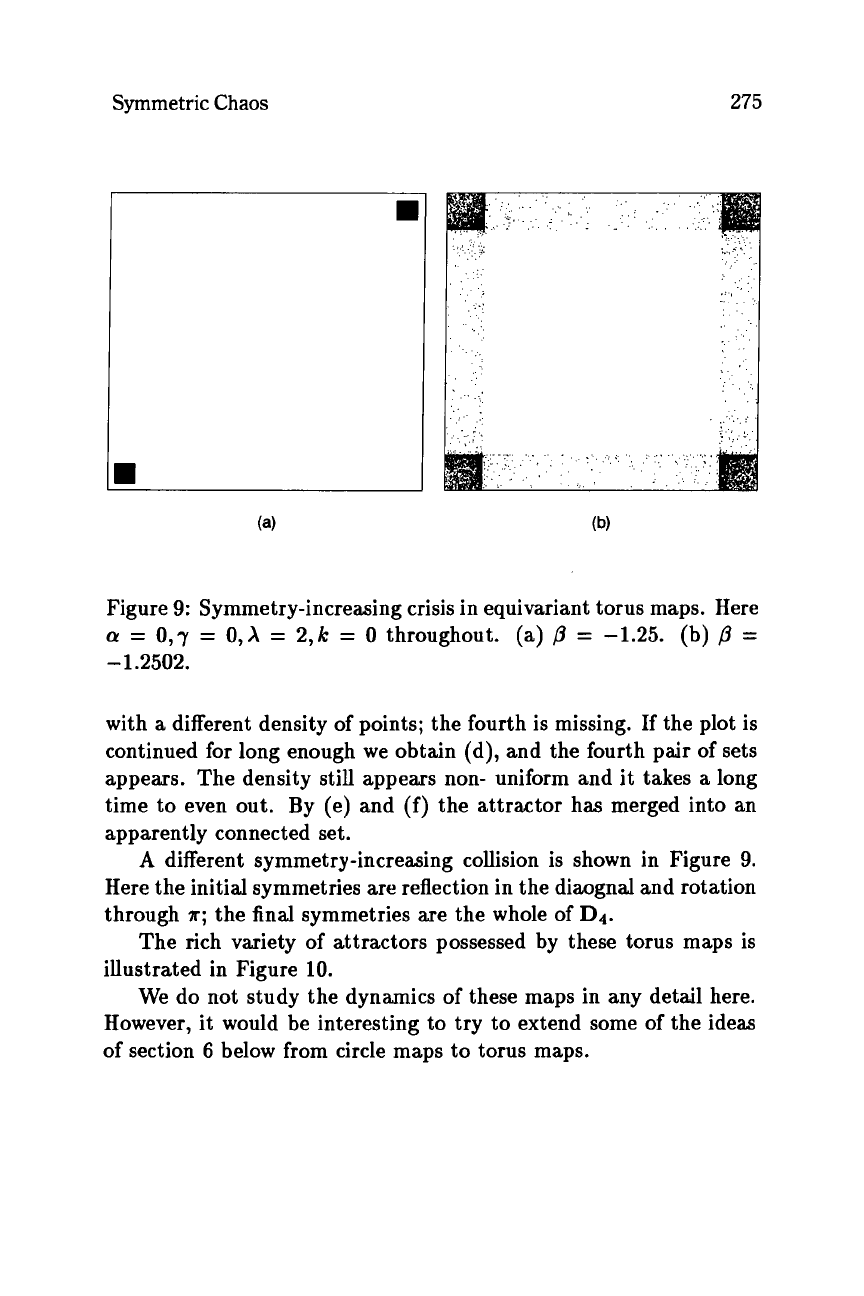
Figure
9:
Symmetry-increasing crisis in equivariant torus maps. Here
a
=
0,7
=
0,X
=
2,k
=
0
throughout.
(a)
p
=
-1.25.
(b)
p
=
-1.2502.
with
a
different density of points; the fourth is missing. If the plot is
continued for long enough we obtain (d), and the fourth pair of sets
appears. The density still appears non- uniform and it takes
a
long
time to even out. By (e) and
(f)
the attractor has merged into an
apparently connected set.
A
different symmetry-increasing collision is shown in Figure
9.
Here the initial symmetries
are
reflection in the diaognal and rotation
through
~r;
the final symmetries are the whole of
Dq.
The rich variety of attractors possessed by these torus maps is
illustrated in Figure
10.
We do not study the dynamics
of
these maps in any detail here.
However, it would be interesting to try to extend some of the ideas
of section
6
below from circle maps to torus maps.

276
Greg
King
and
Ian
Stewart
Figure
10:
Further examples
of
attractors
of
equivariant torus maps.
(a)
a
=
.2,p
=
.23,y
=
.1,X
=
.25,
k
=
2.
(b)
cr
=
-.7,
p
=
.4,
(d)
a
=
.55,
p
=
.33,
7
=
.19,
X
=
.15,
k
=
1.
(e)
a
=
-55,
p
=
.33,
y
=
.19,
A
=
.05,
k
=
1.
(f)
a
=
.42,
p
=
.33, y
=
.19,
X
=
.05,
k
=
1.
y
=
.l,
X
=
.25,
k
=
1.
(c)
=
0,p
=
-.13,
7
=
.26,
X
=
-.7,
k
=
5.

Symmetric
Chaos
277
5
Useful
Theorems
In
this section we collect together various useful results from the
'folklore' of symmetric chaos. The first concerns the question
of
obtaining
di'eomorphisms
that exhibit 'exotic' behaviour. The sec-
ond explains how symmetry-increasing crises come about. The third
relates to the possible isotropy subgroups of non- point attractors,
especially strange ones.
5.1
Shadow
Lift Lemma
Most
of
the examples that we discuss in this paper are mappings
rather than diffeomorphisms, that is, they are usually non- invert-
ible. However, Poincar6 maps derived from continuous systems are
always diffeomorphisms. Inasmuch
as
much of the observed struc-
ture in strange attractors of maps seems
to
be related to the critical
values
(see
section 4.2) one may ask whether mappings are really the
appropriate objects to study.
In fact they are: we now show that structure observed in map-
pings in dimension
n
can be found in diffeomorphisms in dimension
2n.
We begin with some definitions.
R"
is
a
mapping. Let
(yt)
be
a
sequence
of
points in
R"
and let
c
>
0.
We say that
(yt)
€-shadows
f
for
20
5
t
5
tl,
or
is an
c-
pseudoorbit
of
f,
if for
all
t
with
to
5
t
5
tl
we
have
JJyt+l
-
f(yt)Jl
<
6.
That is, the points of the sequence
(yt)
for
t
in the interval considered look like
an
orbit of
f,
except for
a
perturbation of size
<
at each iteration. The
shadowing lemma
of Bowen [4],
see
also Guckenheimer and Holmes (221 p.251, states
that under such conditions, then for any
6
>
0
we
can choose
E
small
enough such that there exists an orbit
(zt)
of
f
with
llyt
-
zt)ll
<
6.
That
is,
an E-pseudoorbit lies within
6
of
a
true orbit. This result
is often invoked to justify the use of computer graphics to display
the structure of strange attractors, when by definition trajectories
on such attractors are subject to exponential divergence and hence
to numerical instability.
Our next result explains the relevance of phenomena observed in
mappings to phenomena that can occur in diffeomorphisms.
Suppose that
f
:
R"

278
Greg
King
and
Ian
Stewart
Lemma
5.1
(Shadow-
Lifting)
Suppose that
f
:
R"
+
R"
is
a
G-equivariant mapping, having
a
compact attractor
A.
Let and
to
<
tl
be given.
For
any
c
>
0
define
the mapping
F
:
R"
x
Rn
+
R"
x
R"
by
Then:
(a)
F
is
a
diffeomorphism.
(b)
F
is equivariant for the diagonal action
7.(z,y)
=
(7.s,7.y)
of
G
on
R"
of
R"
x
R".
(c) If
A
lies within
a
ball centre the origin of radius
B,
then
for
any
yo
E
A
the sequence
yt
=
?rl(Ft(yo))
&-shadows
f,
where
?rl
is
projection onto the first factor
R"
of
R"
x
R".
Proof
(a)
The inverse of
F
is G where
(b) Let
7 E G. Then
7.F(z,y)
=
7.(cy
+
f(z),z)
=
(~.(cy
+
(c) By definition we have
Il?r1(F(s,y)
-
f(z)ll
=
IIcyII,
where
y
E
A.
f(4,
7.4
=
(€74+7.f(4,7.4
=
(c7.y+f(7.4,74
=
F(7+
7.9).
The result is now immediate.
We call
F
the
€-rift
of
f.
Applied to the logistic map it produces
the Hdnon map; applied to the odd logistic map it produces an 'ap-
proximate Poincard map' used by Holmes
[23].
If we take
c
small
enough, then the shadow lifting lemma shows that projections onto
the first factor of attractors of
F
are arbitrarily close
to
attractors
of
f.
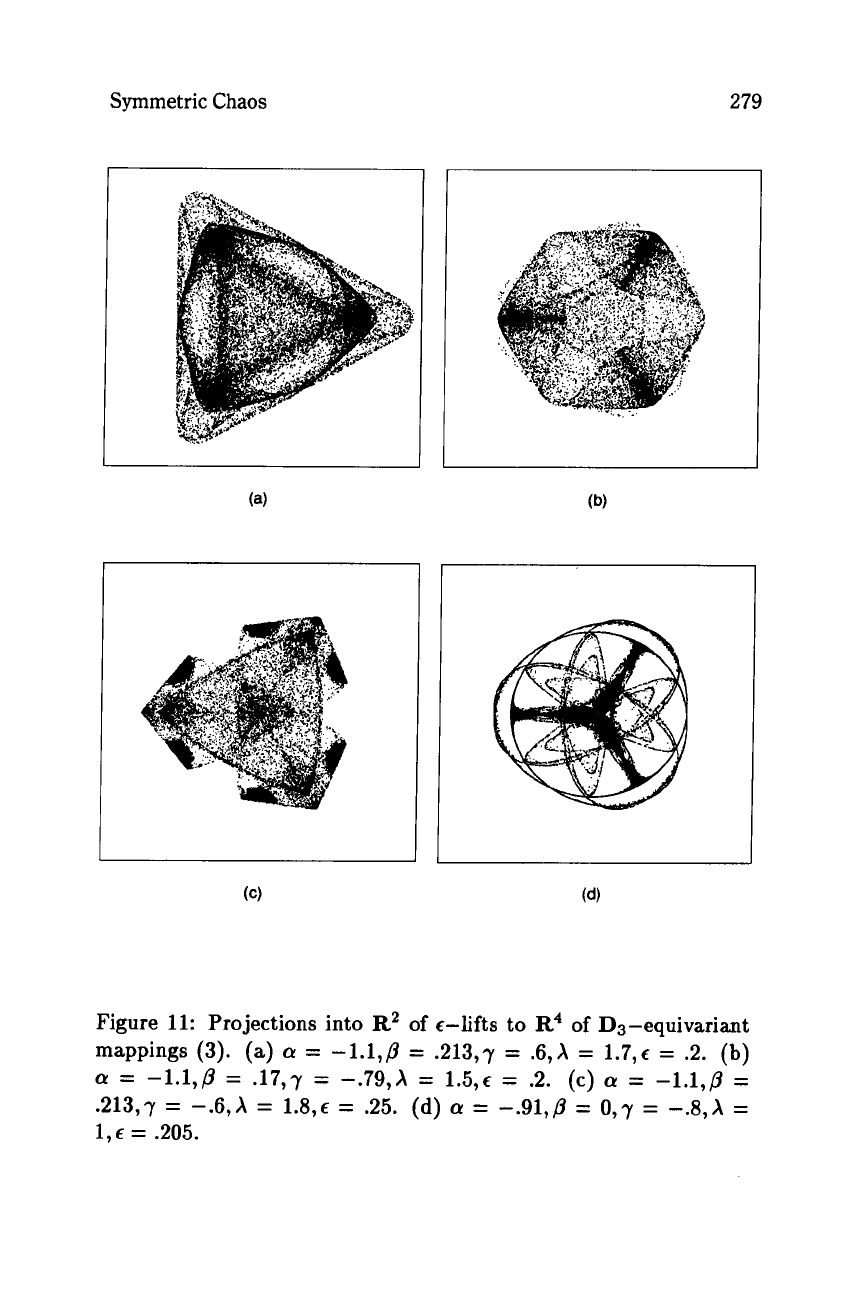
In practice, even when
c
is quite large
a
lot
of
the 'strange' struc-
ture
sf
the attractors
off
can be observed, although not
at
precisely
the same parameter values for
a,
p,
7,
A:
see
Figure
11.
Moreover, it is easier to find interesting behaviour for mappings
in low dimensions than it is for diffeomorphisms. In particular,
al-
though
as
we
have already observed no D3-equivariant mapping
of
Symmetric
Chaos
279
..
..
Figure
11:
Projections into
R2
of
c-lifts to
R4
of D3-equivariant
mappings
(3).
(a)
a
=
-1.1,p
=
.213,7
=
.6,X
=
1.7,~
=
.2.
(b)
.213,7
=
-.6,X
=
1.8,~
=
.25.
(d)
(Y
=
-.91,p
=
O,7
=
-.&A
=
(Y
=
-1.1,p
=
.17,7
=
-.79,X
=
1.5,~
=
2.
(c)
a
=
-1.1,p
=
1,~
=
.205.
