Ames W.F., Roger C. Nonlinear equations in the applied sciences. Volume 185
Подождите немного. Документ загружается.


280
Greg
King
and
Ian
Stewart
the plane can have
a
fully symmetric attractor, this can occur for
Ds-equivariant mappings on
R4
(modulo the conjecture that what
appear on the computer screen
to
be strange attractors really
are
st range
at
tractors).
5.2
Symmetry-increasing Crises
In this section we 'explain' why collisions
of
strange attractors in
equivariant systems tend to increase symmetry, following arguments
of
Chossat and Golubitsky
[lo].
Let
f
:
R"
+
R"
be
a
G-equivariant
mapping and let
A
be an attractor for
f,
satisfying properties (a-c)
of
section
3.
Proposition
5.2
(Symmetry-
Increasing
Crises)
Let
f
:
R"
+
R"
be
a
G-equivariant mapping and let
A
be an
attractor
for
f
in the above sense. Suppose that
for
some
7
E
G
we
have
An7(A)
#
0
Then
7(A)
=
A.
Proof
Let
T
=
{fn(z)}
be
a
dense orbit in
A,
and
suppose
we
can show
that
o(x)
=
A
for
every
z
E
T.
(5)
Let
U
be an open neighbourhood of
A
satisfying (c) above and define
Q
=
y(U)
fl
U.
By assumption
U
is open
and
non- empty. Since
T
is
denseinAandQilA#Q,wehaveQilT#fl.
LetxEQflT. Then
o(x)
E
A.
Since x
E
7(U)
we
also
have ~(x)
C
7(A).
Therefore
A
c
y(A).
Reversing the roles
of
A
and
?(A)
we obtain
7(A)
C
A.
Thus
A
=
r(A).
It remains to prove
5.
Let x
E
T
and let
a
E
A.
We show
a
E
~(x).
If
a
@
T
then by density of
T,
a
E
~(x).
To
deal with
the case when
a
E
T
we choose
u
so
that the orbit
of
u
is
T,
and
then it is enough to show that
~(u)
includes
T,
because ~(x)
=
o(fk(u))
=
fk(u(u))
for some
k.
But this follows from the recurrence
property
!(A)
=
A,
which implies that there is
a
sequence of iterates
ftn(21)
+
21.

Symmetric
Chaos
28
1
This proposition implies that when
two
conjugate attractors
A
and
7(A)
collide, then the result includes
7
as
a
symmetry. Moreover,
if
A
already has symmetry
AA
then it is easy to check that the new
combined attractor has symmetry
(AA,~)
generated by
AA
and
7.
Thus it is
not
a
surprise to find that crises increase symmetry.
5.3
Isotropy
For
a
given group
G
acting on
R"
by
a
given representation, it is
known that in general the isotropy subgroups
of
single points do
not comprise all possible (closed) subgroups of
G.
For example the
isotropy subgroups
of
D,
acting in its standard representation on
R2
are (up
to
conjugacy)
1,
Zz,
and
D3;
the subgroup
23
cannot occur.
What about isotropy subgroups
of
subsets
of
R"?
In particular,
can the isotropy subgroups
of
non-point attractors differ from those
of
single points?
Until recently the only isotropy groups
of
attractors encountered
in numerical experiments on the family
(3)
were
1,
Z2,
D3
-
the
same
as
for points.
It
was
unknown whether
Z3
can occur. The
answer (numerically,
at
least) is provided by Figures
12,
13,
which
we stumbled upon by accident. This attractor emerges only after
a
long transient, which looks very similar
to
the attractors that occur
at nearby parameter values. It seems to be rather fragile.
We shed
a
little more light on the question by sketching
a
con-
struction showing that when
G
acts faithfully, every finite cyclic sub-
group can be an isotropy group
of
an attractor of some G-equivariant
mapping.
Let
G
be compact, acting linearly and (without loss of generality)
orthogonally. Consider
a
cyclic group
H
=
Zm
=
(l,~,.
. .
,7m-1).
Suppose that
Do
is
a
fundamental domain
for
the H-action on the
unit sphere
Sn-',
so
that the cone
D
on
DO
is
a
fundamental domain
for
H
acting on
R".
That is,
the union is disjoint except for the origin, and
D
contains
a
non-
empty open set
U.

282
Greg
King
and
Ian
Stewart
I
Figure 12: Zs-symmetric attractor for the mapping (3) with param-
eter values
a
=
-.9,p
=
O,7
=
.8,X
=
1.25002.
Although the
attractor here looks periodic (with fairly large period) close-ups of
individual specks (Figure 13) reveal a structure similar to that of the
HCnon attractor.

Symmetric
Chaos
/
Figure
13:
Close-up of speck in Figure
12.
283
Choose
a
map
4
:
U
-+
U
such that
q5m
has an attractor
A,
for
example the Hdnon map restricted to a suitable disc. (The recurrence
of the Hdnon map together with its lack
of
periodicity presumably
implies that this attractor is the same
as
that of
4,
but we do not
need to know this here.) Define
v
=
mijlyk(U)
k=O
(7)
and define
6
:
V
-,
V
as follows.
If
x
E
rk(U)
then
d(z)
=
7.4(x)
E
rk+'(
U).
Then extend
4
to
a
continuous mapping on
Rn
and average
over
G
to obtain an equivariant extension, which we
also
cad
4.
The
map
6
is similar to
4
except that it moves 'one place
on'
from
rk(U)
to
rk+'(U).
Thus
dm(u)
=
q5"(u)
for all
u
E
U.
Therefore
4
has an
attractor
B
formed by
m
disjoint copies
of
A,

284
Greg
King
and
Ian
Stewart
and
y(B)
=
B.
We conclude that the isotropy subgroup of
B
con-
tains
H.
6
Symmetry-locking and Equivariant Knead-
ing Theory
We now describe some initial steps towards
a
rigorous theory
of
equivariant chaos. Krupa and Roberts
[25]
have developed equiv-
ariant versions
of
symbolic dynamics and kneading theory to study
circle maps that are equivariant under the action
of
the dihedral
group
D,.
In this section we summarize some of their ideas, which
are among the most substantial rigorously proved results on the dy-
namics of maps with symmetry.
Following standard practice they employ circle maps
as
models
for
the following dynamical situation. Consider
a
dynamical sys-
tem with Z, symmetry, in which there is
a
rotating wave with
2,
symmetry. Assume that this undergoes Hopf bifurcation
to
create
a
torus with Z, symmetry, and that this torus subsequently breaks
up.
If
we consider
a
Poincar6 section then we have
a
Z,-equivariant
Poincar6 mapping
q5
defined on an annulus
(a
neighbourhood
of
the
cross-section
of
the torus, which is
a
circle). Assume that the torus
is strongly stable,
so
that
4
is strongly contracting from the annulus
to the circle. Then we may approximate the important dynamics
of
q5
by its restriction to the circle. After the torus breaks down this
approximation remains valid, and we can expect to observe chaotic
dynamics in the circle map.
To
keep the discussion specific, consider the family of
Arnold
maps
fw,
:
s'
+
s'
defined by
(9)
P
fuF(x)
=
x
+
w
-
-
sin
2nkx
(mod
1).
2nk
This has
a
cyclic symmetry group
G
=
Zk defined by
x
w
x
+
f
,
s
=
0,.
. .
,
k
-
1.
We study how the orbital symmetry group
As
varies

Symmetric
Chaos
285
with the parameters
w
and
p
for
x
belonging to attractors
of
f.
Here
S’
=
R/Z
is the circle.
For certain values
of
w
the map
(9)
has
a
further symmetry. For
example, if
w
=
0,
i,
then
f,,
is equivariant under
x
H
-x.
More
generally, if
w
=
$
then
for
T
=
0,.
.
.
,2k
-
1.
This can be thought of
as
Dk-
symmetry in
which the group actions on source and target are different. In par-
ticular it implies that all points
x
=
$
are periodic. These periodic
orbits have symmetry group
D(k,,)
where
=
in lowest terms.
In Figure 14 we give some examples of how the maps
f,,
bifurcate
for various fixed rational
w,
as
p
varies. In cases (a) and (b) we have
chosen
w
and
k
to produce the
Dk
symmetry just mentioned. In
contrast, in case (c) there is only
Zk
symmetry. The figures are
drawn in pairs. In the first of each pair,
p
runs horizontally and the
coordinate
2
on the circle runs vertically from
0
to
1,
so
top and
bottom are identified. In the second polar coordinate version,
p
is
the radial coordinate and the angular variable is
2rx.
The figures
are drawn by very slowly ‘ramping’ the value of
p,
that is, increasing
it by
0.0001
at each iteration; meanwhile the new value
of
2
is given
by formula
(9).
The entire bifurcation diagram is obtained
as
a
trajectory of the resulting dynamical system.
In (a) we have
k
=
5 and the overall symmetry is
D5.
We first
see
a
period-10 point whose orbit has
D5
symmetry. The first bifurca-
tion is period-doubling to
a
period-20 point, still with
D5
symmetry.
The symmetry breaks
to
25
at
the next bifurcation (though this
is
hard to
see
because of the small scale). It is followed by
a
period-
doubling cascade that preserves the remaining symmetry. Then
a
mini-crisis restores the symmetry to
D5,
and the attractor grows
without further crises until it occupies the entire circle. This chaotic
band is punctuated by periodic windows, in which the symmetries
also change. Then the chaos vanishes leaving
a
period-5 point with
25
symmetry: this undergoes its own period-doubling cascade, still
with
2s
symmetry. Another crisis again restores
D5
symmetry. The
second chaotic band, also containing periodic windows, terminates

286
Greg
King and
Ian
Stewart
Figure
14:
Examples of symmetry-locking in torus maps, shown in
Cartesian and polar bifurcation diagrams. Here
p
runs from
0
to
10.
3
5
7
(a)
k
=
5,w
=
=.
(b)
k
=
6,w
=
i2.
(c)
k
=
3,w
=
3.

Symmetric
Chaos 287
by the creation of
a
period-10 point with
D5
symmetry, followed by
a
symmetry-breaking pitchfork bifurcation to
25
symmetry
...
and
so
on.
Case (b), in which
k
=
6,
is slightly different. Here the initial
bifurcation is
a
symmetry-breaking pitchfork, starting
a
period- dou-
bling cascade, and
at
this stage the orbit has
D3
symmetry.
(As
well
as
the obvious translations there
is
a
combination of
a
reflection and
a
translation.) There is
a
tiny local crisis that partially restores the
symmetry, and
a
second crisis to restore full
D6
symmetry. The
chaotic band terminates in
a
fixed point with
Z2
symmetry. It un-
dergoes
a
symmetry-breaking pitchfork to trid symmetry and then
a
period- doubling cascade, still with trivial symmetry, until two suc-
cessive crises restore
22
and then
D6
symmetry. The second chaotic
band terminates in
a
D6-symmetric periodic point, which undergoes
a
pitchfork
to
Z6 symmetry and period-doubles; again two successive
crises restore the symmetries. The third chaotic band terminates in
a
periodic point with
Z3
symmetry
...
and
so
on.
Case
(c) is included merely to show that when
w
=
p/q
and
q
#
2k,
new phenomena occur
as
well
as
those just described. Some
of the structure visible is an artefact
of
the drawing procedure: in
particular the dark band towards the left-hand end mainly corre-
sponds to quasiperiodic motion in which the whole circle becomes
the attractor. But again we
see
broken symmetries and symmetry-
increasing crises.
Krupa and Roberts
[25]
systematize these observations and prove
theorems that limit
or
pin down the possible phenomena. First, lift
fwr
to
a
map
FWr
:
R
-,
R
with the same formula
as
fwr
(but not taken (mod
1)).
Define the
rotation intervalp(j)
as
follows.
If
x
E
S'
then
p(x,
j)
=
{z
E
R
I
z
is
a
limit point of
[
F"(y)
-
72.').
(11)
n
where
y
is
a
lift of
x
to
R,
and then set
P(f)
=
u
P(M
ZESl
288
Greg
King
and
Ian
Stewart
f
not
homeomorphism
1
f
homeomorphism
Figure
15:
Schematic of an Arnold tongue for the torus map (9).
which is known to be
a
closed interval. The end-points of
p(f)
vary
continuously with
f
in the
Co
topology.
If
f
is monotonic, that is,
a
homeomorphism, then the rotation intervals are points and there is
a
unique rotation number. In general, if
p(f)
is
a
single point, the
we say that
f
is
frequency- locked.
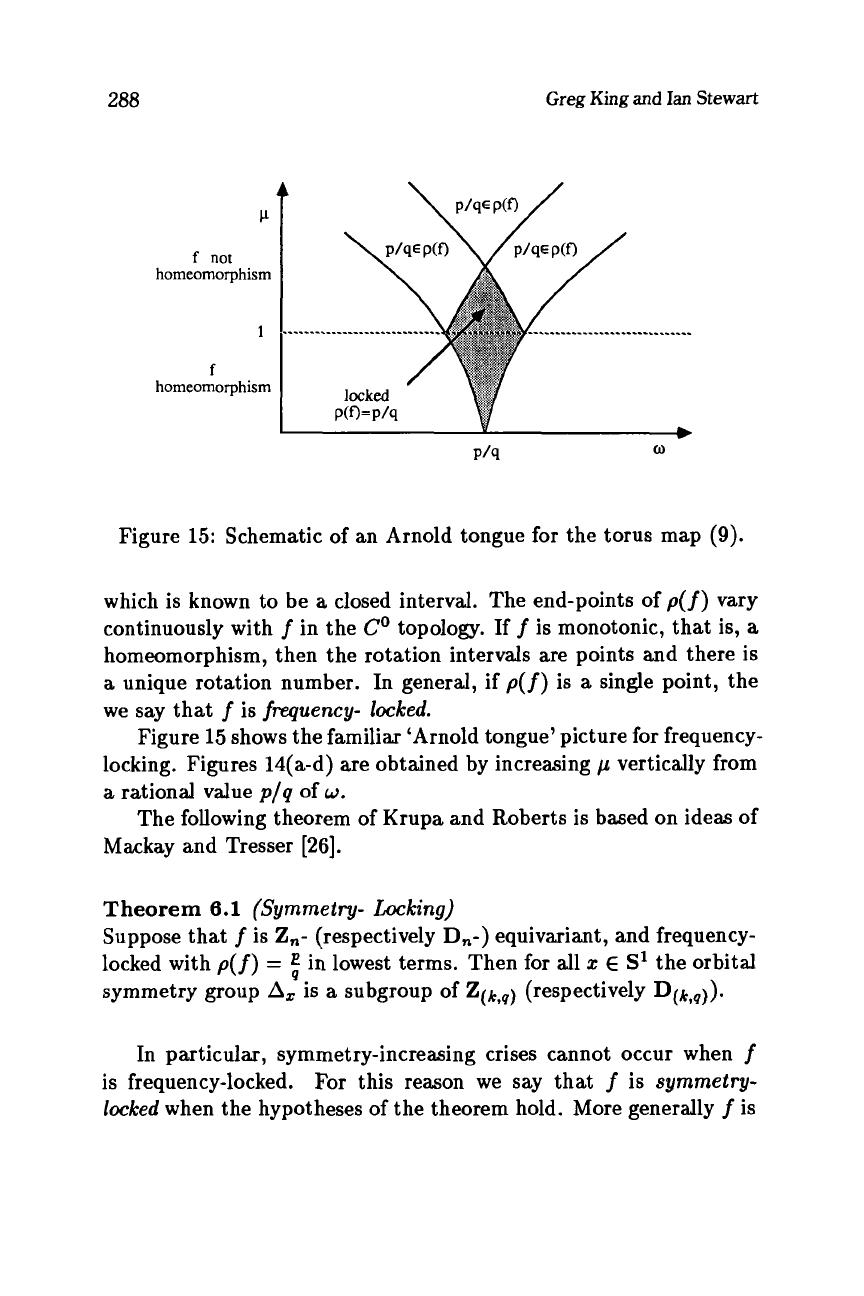
Figure
15
shows the familiar 'Arnold tongue' picture for frequency-
locking. Figures 14(a-d) are obtained by increasing
p
vertically from
a
rational value
p/q
of
w.
The following theorem of Krupa and Roberts is based
on
ideas of
Mackay and Tresser
[26].
Theorem
6.1
(Syrnmetry- Locking)
Suppose that
f
is
Z,-
(respectively
Dn-)
equivariant, and frequency-
locked with
p(f)
=
:
in lowest terms. Then for all
x
€
S'
the orbital
symmetry group
A,
is
a
subgroup of
Z(k,*)
(respectively
D(k,*)).
In particular, symmetry-increasing crises cannot occur when
f
is frequency-locked.
For
this reason we say that
f
is
symmetry-
locked
when the hypotheses of the theorem hold. More generally
f
is

Symmetric Chaos
289
symmetry-locked in some region of parameter space if there exists
a
subgroup
A
of
G
such that
A,
C
A
for
all
x
when the parameters lie
in that region. However, even when
f
is symmetry-locked there may
exist windows in which symmetry is first broken and then restored
via
a
crisis.
Crises happen on the boundary
of
the shaded region in Figure
15.
The theorem is sharp in the sense that if
w
is irrational and
w
E
p(f),
then there exists
z
such that
C,
=
Zk
(respectively
Dk).
Now we sketch how the existing theory
of
symbolic dynamics of
one- humped maps (such
as
the logistic map) can be applied to this
equivariant case.
(See
Devaney [14] for an introduction
to
symbolic
dynamics.) Consider
a
parameter window with
w
constant and
p
increasing, such that there is
a
saddle-node bifurcation to
a
period
q
point. This occurs when the graph of
fQ
becomes tangent to the
diagonal,
as
in Figure 16(a). This bifurcation creates an invariant
interval
I
on which the graph of
fQ
resembles
a
one-humped map.
The dynamics of the system is then largely controlled by that
of
the
one-humped map; however, in addition we must take account of the
manner in which
f
permutes the intervals
I,
f(I),
. . .
,
fk-’(I)
and
the symmetries. These latter are essentially combinatorial issues and
do not pose any conceptual difficulties (although keeping the details
straight is
far
from easy!). Figures 16(b-e) show the ‘typical’
pro-
gression
of
the bifurcation
as
p
increases: appropriate ‘semi-global’
monotonicity conditions are required to ensure that these pictures are
actually valid, but in examples those conditions commonly do hold.
The result is that
fQ
passes through an entire bifurcation sequence
for the one-humped map: initial period-doublings in
a
Feigenbaum
cascade, followed by chaos, with periodic windows, Sarkovsii order-
ing, and
so
forth. See Collet and Eckmann
[ll]
or Devaney [14].
Again we observe the occurrence
of
symmetry-locking. Through-
out Figures 16(a-d) the interval that defines the horizontal edge of the
boxes is invariant, ceasing to be invariant only at the stage shown in
Figure 16(d). While that interval remains invariant it is not possible
to
regain (through crises) any symmetries lost at the initial saddle-
node bifurcation. Thus
we
have
a
saddle-node symmety-locking win-
dow.
The location
of
such windows can be found using symbolic
