Alfred DeMaris - Regression with Social Data, Modeling Continuous and Limited Response Variables
Подождите немного. Документ загружается.


increase in complexity would be worthwhile. Hence, I choose the quadratic model as
exhibiting maximum parsimony while capturing most of the nonlinearity in the data.
Additionally, the quadratic model is most consistent with theoretical expectation.
Centering. For models 2 and 3 in Table 5.1, I employ the centered version of age
decile and then form the quadratic term by squaring this centered variable. This has
two advantages. First, it renders the main effect of age decile interpretable in the
quadratic model. The partial slope for age decile in model (5.5), which captures the
“effect” of age decile on sexual frequency, is β 2γ age decile. The main effect of
age decile, or β, is the effect when age decile is zero, since in this case the “2γ age
decile” term disappears. If age decile is uncentered, this effect has no meaning, since
age decile, which begins at the value 1, cannot possibly take on the value zero.
However, if age decile is centered, it is zero whenever age decile is at its mean. Thus,
β is the effect of age decile at its mean. Moreover, the test of significance of b, the
sample estimate of β, is a test for whether the impact of increasing age (in deciles)
is significant at its mean value.
The second advantage of centering has to do with collinearity. Recall from
Chapter 3 that it was important to center the continuous variables involved in cross-
product terms in order to reduce potential collinearity problems. For the same rea-
son, we want to center X before creating higher-order powers of X (e.g., X
2
, X
3
) to
include in the model. As an example, without centering, age and age-squared are
correlated .9737, producing VIF’s (not shown) of 19.26 for each coefficient in the
quadratic model. After centering, the correlation is reduced to .1, and the VIF’s for
each coefficient are only 1.01. At the least, collinearity inflates the sampling variance
of one’s estimators, which tends to reduce the power of tests for the coefficients. In
this case, it has relatively little effect on the estimates, however, and both are quite
significant in the uncentered version of the model as well. In this model (not shown),
the coefficient for age decile, or b, is .422, while the coefficient for (age decile)
2
,or
g,is.065. Although σ
ˆ
g
is no different than for the model using the centered vari-
ables, σ
ˆ
b
is about four times larger in the uncentered, versus the centered, model.
The quadratic effect, .065, is the same in both models. The main effects in the cen-
tered and uncentered models are not directly comparable, since the value of .422 in
the uncentered model is the effect when age decile is zero. To make them compara-
ble, consider the effect of age decile at its mean for the uncentered model. As the
mean of age decile is 5.279, the effect is . 422 2(.065) (5.279) .264, com-
pared to .26 in the centered model. Both models apparently give rise to compara-
ble estimates of age decile’s effect on sexual frequency.
Interpreting Quadratic Models
The use of age decile in place of the continuous variable, age, was necessary for test-
ing various alternatives to the unconstrained model, since it allowed for the creation
of nested models. However, once the quadratic model was chosen, it was reestimated
using continuous age in place of age decile. Again, age was centered prior to taking
its square. The results are shown as model 1 in Table 5.2. The effects of both age and
COMMON NONLINEAR FUNCTIONS OF X 175
c05.qxd 8/27/2004 2:53 PM Page 175

176 MODELING NONLINEARITY
age
2
are significant, and both are negative, again suggesting a segment I curve, the
pattern exhibited in Figure 5.8. The partial slope for age is .04 2(.001) age. (The
effects are smaller than for the age decile model, since the units of age are now sin-
gle years instead of deciles.) Thus, at mean age (age 44.455) the partial slope
is .04; at 1 standard deviation above mean age (age 61.229) it is .04 2(.001)
(16.774) .074; and at 2 standard deviations above mean age (age 78.003)
it is .04 2(.001)(33.548) .107. These calculations suggest an accelerating
decline in sexual frequency with advancing age, as was expected.
Unit Impact versus Partial Derivative. Recall from Chapter 2 the distinction
between the unit impact of X [the change in E(Y ) for a unit increase in X, at x] and
the partial derivative with respect to X [the instantaneous change in E(Y ) with
change in X, at x]. As mentioned in Chapter 2, these are identical in linear models.
However, in nonlinear models they are different quantities. The partial derivative for
the quadratic model [e.g., model (5.1)] at a particular x is, as noted, β
1
2β
2
x. The
unit impact, however, is
E(Y 冟x 1) E(Y 冟 x) β
0
β
1
(x 1) β
2
(x 1)
2
(β
0
β
1
x β
2
x
2
)
β
0
β
1
x β
1
β
2
x
2
2β
2
x β
2
β
0
β
1
x β
2
x
2
β
1
β
2
2β
2
x.
How much difference does this really make? Actually, it doesn’t make much difference
as long as a unit change in X is a relatively small change. In model 1 in Table 5.2, for
example, the difference is .04 2(.001)x .04 .002x for the partial derivative,
versus .04 .001 2(.001)x .041 .002x for the unit impact. So, for example,
at 1 standard deviation above mean age the partial derivative with respect to age
is .074 and the unit impact is .075. In this case to interpret the partial derivative as
Table 5.2 Curvilinear and Interaction Models for the Regression of Frequency
of Sex on Age and Health for 2320 Respondents in the 1998 GSS
Regressor Model 1 Model 2 Model 3 Model 4
Intercept 3.113*** 3.109*** 2.834*** 3.128***
Age .040*** .037*** .048*** .039***
Age
2
.001*** .001*** .0011***
Health .241*** .225*** .410***
Age health .008** .012***
Age
2
health .0007***
RSS 1981.836 2066.429 1841.966 2142.310
MSE 2.987 2.952 3.049 2.922
R
2
.223 .232 .207 .241
Note: Age and health are centered, and all higher-order terms involving these variables use their
centered versions.
*p .05. ** p .01. *** p .001.
c05.qxd 8/27/2004 2:53 PM Page 176

the approximate change in average sexual frequency for a year’s (i.e., a unit of age)
increase in age is pretty accurate.
But if a unit increase represents a relatively large change in X, approximating the
unit impact with the partial derivative can be misleading. As an example, Lennon and
Rosenfield (1994) investigated the impact of perceived fairness in the household divi-
sion of labor on depressive symptomatology among employed wives, using a quad-
ratic effect of fairness. Perceived fairness was coded 1 for “very unfair to me” (i.e.,
the wife),.5 for “unfair to me,” 0 for “fair to both of us,” .5 for “unfair to my
spouse,” and 1 for “very unfair to my spouse.” Actually, I prefer to refer to this as a
scale of overbenefit, since the highest score represents maximum overbenefit,
whereas maximum fairness occurs in the middle of the scale (see also Longmore and
DeMaris, 1997). According to equity theory (Walster et al., 1978) people experience
distress when they are either underbenefited or overbenefited. With this in mind, the
authors expected that depressive symptomatology would exhibit a U-shaped relation-
ship with overbenefit. Increases in the scale away from underbenefit and in the direc-
tion of fairness should reduce depressive symptoms, whereas increases away from
fairness and in the direction of overbenefit should again increase depressive symp-
toms. The coefficients for overbenefit and its square were, respectively, .086 and .188.
Therefore, the partial derivative is .086 2(.188) overbenefit, while the unit impact is
.086 .188 2(.188) overbenefit. Using the partial derivative to approximate a
change in average depressive symptomatology for a unit increase in overbenefit at the
value of “very unfair to me” on the scale, we get a value of .086 2(.188)(1).29.
In actuality, a unit increase in the scale is associated with a change of .086 .188
2(.188)(1) .102. At the value of “fair to both,” the partial derivative estimates
the change as .086, whereas the unit impact is actually .086 .188 .274. In this
case, the partial derivative is not a particularly good approximation to the unit impact.
Whether this is a problem depends on how important it is to be accurate about the esti-
mated effect of a “unit increase” in the explanatory variable.
NONLINEAR INTERACTION
In Chapters 3 and 4 I discussed various interaction models. However, all of these
involved linear interactions, in which the impact of X might change over levels of Z,
but the relationship between Y and X at each z was always linear. In this section I
consider nonlinear interaction models, in which the nonlinear relationship between
Y and X varies as a function of Z. To motivate interest in the topic, let’s reexamine
the relationship between age and sexual frequency. Prior research on sexual fre-
quency (e.g., Rao and DeMaris, 1995) suggests that those in better health have sex
more often. I would go one step beyond this and suggest that health and age should
interact in their effects on sexual frequency. I have already shown that there is a non-
linear decline in sexual frequency with age. I further hypothesize that the nonlinear
decline in sexual frequency with advancing age will be less pronounced for those in
better, as opposed to poorer, health. This is a nonlinear interaction effect, and we
must first consider how to model it.
NONLINEAR INTERACTION 177
c05.qxd 8/27/2004 2:53 PM Page 177

Once again, I rely on the first partial derivative to define nonlinear interaction in
X. In a model for Y containing the variables X and Z, if the first partial derivative of
Y with respect to X is a function of both X and Z, the model is said to be character-
ized by a nonlinear interaction in X. If the first partial derivative of Y with respect to
X is only a function of Z but not X, the interaction is linear in X. Let’s examine a
series of quadratic models containing X and Z to see how this definition applies. In
model (5.6), Z is added purely as another covariate:
E(Y ) β
0
β
1
X β
2
X
2
β
3
Z. (5.6)
The effect of X (i.e., ∂[E(Y)]/∂X) is β
1
2β
2
X. As this is not a function of Z, there is
no interaction effect here. Thus the curves relating Y to X at each level of Z are par-
allel. Moreover, the curves are identical in shape since, in particular, the departure
from linearity, β
2
, is not a function of Z.
Model (5.7) adds the cross-product of X with Z:
E(Y ) β
0
β
1
X β
2
X
2
β
3
Z β
4
XZ. (5.7)
The effect of X is β
1
2β
2
X β
4
Z. This is a nonlinear interaction effect, since the
term is a function of both X and Z. This means that the curves relating Y to X over
levels of Z will not be parallel. However, they will be similar in shape since the
departure from linearity is still β
2
, which is not a function of Z. Notice that with
respect to Z, the interaction is linear because ∂[E(Y)]/∂Z is β
3
β
4
X. This is just a
conventional linear interaction, as this effect is not also a function of Z.
Model (5.8) adds the cross-product of X
2
with Z:
E(Y ) β
0
β
1
X β
2
X
2
β
3
Z β
4
XZ β
5
X
2
Z. (5.8)
First, you should notice the hierarchical nature of these successive equations. For
every higher-order term in a given equation, all the lower-order components are also
in the equation. This is especially important to remember in equation (5.8), as it is
not immediately obvious that the XZ term must be in the equation. But if X
2
Z is in
the equation, we must also have all of its component regressors: X, X
2
, Z, and XZ. To
continue, the effect of X is β
1
2β
2
X β
4
Z 2β
5
XZ. This can be further expressed
as (β
1
β
4
Z) 2(β
2
β
5
Z)X. This makes clear that the effect is of the form
β 2γX, typical of the quadratic model, except that now β, the linear component of
the curve, is (β
1
β
4
Z), and γ, the departure from linearity, is (β
2
β
5
Z). Obviously
this is a nonlinear interaction effect, since this expression is a function of both X and
Z. But in this case, not only are the X–Y curves not parallel, they are also not of the
same shape, since the departure from linearity is now also a function of Z. The effect
of Z, on the other hand, is β
3
β
4
X β
5
X
2
. This, again, is a conventional linear
interaction in Z, since the expression is not a function of Z. In other words, the Z–Y
relationship at each level of X is still linear.
178 MODELING NONLINEARITY
c05.qxd 8/27/2004 2:53 PM Page 178

NONLINEAR INTERACTION 179
Finally, model (5.9) adds the cross-product of X
2
with Z
2
, plus the additional
lower-order components necessitated by this term—Z
2
and XZ
2
:
E(Y) β
0
β
1
X β
2
Z β
3
X
2
β
4
Z
2
β
5
XZ β
6
XZ
2
β
7
X
2
Z β
8
X
2
Z
2
. (5.9)
In this equation, the effect of X can be written (β
1
β
5
Z 2β
6
Z
2
) 2(β
3
β
7
Z
β
8
Z
2
)X, while the effect of Z can be written (β
2
β
5
X β
7
X
2
) 2(β
4
β
6
β
8
X
2
)Z.
In this case, then, we have a nonlinear interaction effect in both X and Z. For either
interaction, the curves relating Y to X (Z) are neither parallel nor of the same shape
across levels of Z (X).
Because model (5.8) is central to testing the hypothesis regarding the age–health
interaction posed above, let’s consider some additional issues concerning this model.
In particular, we can perform global tests of both curvilinearity and interaction by
comparing this model with other selected models (Aiken and West, 1991). If we fac-
tor equation (5.8) as
E(Y ) (β
0
β
3
Z) (β
1
β
4
Z)X (β
2
β
5
Z)X
2
.
Then a test of curvilinearity tests the null hypothesis that the quadratic effect, which
in this case is β
2
β
5
Z, is zero. Assuming that Z is not uniformly zero, this will be
true if β
2
and β
5
are both zero. Hence a global test of curvilinearity is a nested F test
comparing model (5.8) with the usual linear interaction model,
E(Y ) β
0
β
1
X β
2
Z β
3
XZ. (5.10)
To understand the global test of interaction, we factor (5.8) as
E(Y ) β
0
β
1
X β
2
X
2
β
3
Z (β
4
β
5
X)XZ.
The test for interaction involves the null hypothesis that β
4
β
5
X equals zero (i.e.,
that β
4
β
5
0). The appropriate test is the nested test comparing model (5.8) with
model (5.6).
Returning to the GSS98 dataset, where Y sexual frequency, if we let X age
and Z health, model 2 in Table 5.2 estimates equation (5.6), model 3 estimates
equation (5.10), and model 4 estimates equation (5.8). As the table note indicates,
age, health, and all of their higher-order relatives are based on the centered versions
of these variables. It is clear that health has a significantly positive linear effect on
sexual frequency in each model, as one would expect. It also looks like all interac-
tions involving age and health as well as all quadratic terms in age are significant.
Nevertheless, I begin by performing the global tests just outlined. The global test of
curvilinearity compares model 4 with model 3:
F
(2,2314)
51.394.
(2142.310 1841.966)/2
2.922
c05.qxd 8/27/2004 2:53 PM Page 179

180 MODELING NONLINEARITY
The global test of interaction compares model 4 with model 2:
F
(2,2314)
12.984.
Both test statistics are highly significant, with p .00001. Hence, the model for sex-
ual frequency appears to be characterized by both curvilinearity in the relationship
with age and an interaction between age and health in their effects on the response.
To evaluate my hypothesis completely, it is necessary to examine the age–health
interaction effect more closely. From the discussion above, the effect of age is of the
form (β
1
β
4
Z) 2(β
2
β
5
Z)X, which as pointed out earlier, is a nonlinear interac-
tion. Here β
1
is the coefficient of age, β
4
is the coefficient of the age * health cross-
product term, β
2
is the coefficient of age
2
, and β
5
is the coefficient of the age
2
*
health cross-product term. In terms of the coefficient estimates, the effect of age is
(.039 .012 health) 2(.0011 .0007 health) age.
It is instructive to examine the impact of age at particular values of health. At 1 stan-
dard deviation (.815) below mean health, the effect of age is
[.039 .012(.815)] 2[.0011 .0007(.815)] age .049 .0011 age.
At mean health, the effect of age is
[.039 .012(0)] 2[.0011 .0007(0)] age .039 .0022 age.
At 1 standard deviation above mean health, the effect of age is
[.039 .012 (.815)] 2[.0011 .0007(.815)] age .029 .0033 age.
A more complete picture of the impact of age is obtained by evaluating each of
these three partial slopes at selected values of age. In this case I evaluated them at 1
standard deviation below mean age, at mean age, and at 1 standard deviation above
mean age. The results are shown in Table 5.3. Each number in the table is the impact
of age on sexual frequency at selected settings of age and health. The pattern that
emerges is somewhat unusual. Among younger respondents, age apparently has an
adverse effect on sexual activity that is more pronounced for those in poorer health
(reading down the first two columns). However, among the oldest respondents (1
standard deviation above mean age), this effect is reversed, and age has the most
adverse effect among the healthiest respondents (reading down the third column). In
other words, the decline in sexual activity with age is least dramatic for those in bet-
ter health, but only up to a certain age; after that, the decline is more rapid for those
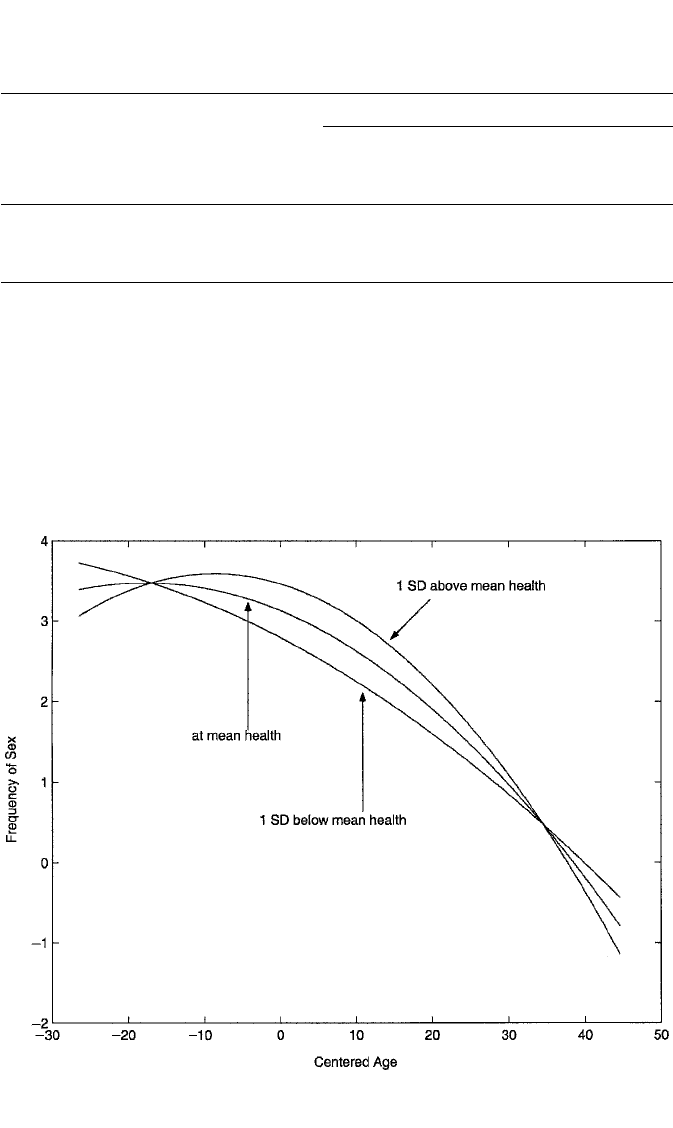
in better health. This is much more easily discerned in Figure 5.9, which graphs the
age–sexual frequency relationship at the three levels of health. As is evident in the
figure, those in poorest health experience a nearly linear decline in sexual frequency
(2142.310 2066.429)/2
2.922
c05.qxd 8/27/2004 2:53 PM Page 180
NONLINEAR INTERACTION 181
Table 5.3 Partial Derivatives with Respect to Age for the Regression of Sexual
Frequency on Age and Health at Selected Values of Age and Health
Value of Age
One Standard One Standard
Deviation Deviation
Value of Health Below Mean Mean Above Mean
One standard deviation below mean .031 .049 .067
Mean .002 .039 .076
One standard deviation above mean .026 .029 .084
Note: Calculations are based on model 4 in Table 5.2.
Figure 5.9 Graph of nonlinear (in age) interaction between age and health in their effects on frequency
of sex.
with age; for those in average health, the decline is much more gradual; and for those
in good health, there is an initial increase in sexual activity with age, followed by a
gradual decline that becomes ever steeper after about age 55 (i.e., 10 years beyond
the mean of 44.455). As the decline in sexual activity with age tends to be most pro-
nounced for the unhealthiest respondents, I consider my hypothesis to be largely
supported.
c05.qxd 8/27/2004 2:53 PM Page 181
182 MODELING NONLINEARITY
Using the same approach, we can recover the partial slopes for the impact of
health at the three settings of age employed above. (This is left as an exercise for the
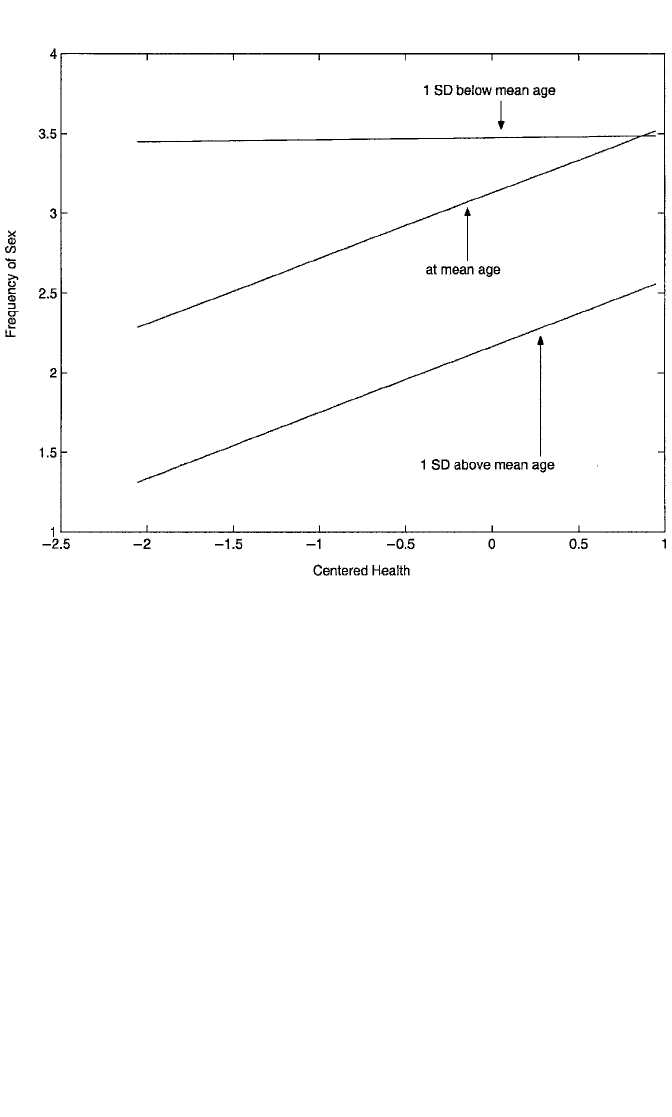
reader.) Recall that in this type of model, the interaction is linear in health. This is
easily revealed by Figure 5.10, in which the relationship between sexual frequency
and health is plotted separately for those who are 1 standard deviation below mean
age, at mean age, and 1 standard deviation above mean age. It appears that health
has little impact on sexual frequency for the youngest respondents; their sexual activ-
ity is uniformly high regardless of health status. However, for those of average age
or older, health appears to have a substantial positive impact, with more sexual activ-
ity being reported by those in better health.
Nonlinear Interaction: Another Example. Another example of a nonlinear interac-
tion, one that does not involve the quadratic model, can be found in Mirowsky and
Hu (1996). They investigated the relationship between income and physical impair-
ment in two national probability samples. Based on an initial investigation of the
bivariate relationship between income and physical impairment, they decided that a
cube-root transformation of income in thousands would best represent the
Figure 5.10 Graph of linear (in health) interaction between age and health in their effects on frequency
of sex.
c05.qxd 8/27/2004 2:53 PM Page 182

relationship. They also allowed this function of income to interact with education.
Their estimated equation takes the form
yˆ a g controls bX
1/3
cZ dZX
1/3
,
(5.11)
where gcontrols is a weighted sum of coefficients times control variables, X is
income in thousands of dollars, and Z is education in years of completed schooling.
The first partial derivative of this equation with respect to X is
∂
∂
X
yˆ
1
3
bX
2/3
1
3
dZX
2/3
b
3
X
2
d
/3
Z
.
As this expression is a function of both X and Z, it is clearly a nonlinear interaction
(also made very clear by their graphs of the income–physical impairment relation-
ship at different levels of education; see Mirowsky and Hu, 1996, Fig. 4).
A sense of the nature of the interaction can be obtained by evaluating the impact
of income at, say, income $10,000, at three levels of education. The coefficients
are b .038 and d .021. In this analysis, Z (i.e., education) is centered, and
although its standard deviation is not given, I estimate it as 3, based on the range of
education. At 1 standard deviation below mean education, the impact of income is
.03
3
8
(
10
.0
2
2
/3
1
)
(3)
.00725.
At mean education, the impact of income is
.03
3
8
(1
0
.
2
0
/3
2
)
1(0)
.00273.
At 1 standard deviation above mean education, the impact of income is
.03
3
8
(1
0
.
2
0
/3
2
)
1(3)
.0018.
It is instructive to repeat these computations for income $25,000. At 1 standard
deviation below mean education, the impact of income is
.03
3
8
(
25
.0
2
2
/3
1
)
(3)
.0039.
At mean education, the impact of income is
.03
3
8
(2
5
.
2
0
/3
2
)
1(0)
.0015.
NONLINEAR INTERACTION 183
c05.qxd 8/27/2004 2:53 PM Page 183

At 1 standard deviation above mean education, the impact of income is
.03
3
8
(2
5
.
2
0
/3
2
)
1(3)
.00097.
What these computations show is that income appears, in general, to reduce physi-
cal impairment. But income has a stronger impact on reducing impairment for those
with less education than for those with more education. Additionally, this trend (i.e.,
the differential impact of income according to education level) becomes less and less
evident at higher levels of income. As a final note, the partial derivative of (5.11) with
respect to Z (i.e., education) is c dX
1/3
. Since this is not a function of Z, the inter-
action is linear in education.
NONLINEAR REGRESSION
In this final section of the chapter, I consider the estimation of essentially nonlinear
models. These are referred to as nonlinear regression models and are typically esti-
mated using nonlinear least squares. To avoid excessive mathematical complexity,
I restrict attention to a relatively simple model yet one that illustrates all of the key
facets of this technique. Table 5.4 presents measurements on the diagnostic quiz and
the score on the final exam for 11 students in my beginning graduate-level statistics
class. The quiz is given during the seventh week of the semester to gauge how well
students are assimilating the material. The final exam is given during the sixteenth
week. Figure 5.11 shows a scatterplot of these variables, with final exam scores plot-
ted against diagnostic quiz scores. There is clearly a strong positive relationship
between the variables but one that does not appear to be linear. In fact, it very much
resembles the pattern exhibited by the function y e
x
in Figure 5.1. Is this reason-
able? Assuming that the diagnostic quiz taps statistical aptitude, the trend in the
figure suggests that an increase in aptitude has an accelerating positive effect on per-
formance in the class. That is, an increase in aptitude has a stronger effect on per-
formance for those who already have considerable aptitude than for those whose
skills are more rudimentary. If this is true, one appropriate model for these data, with
184 MODELING NONLINEARITY
Table 5.4 Score on Diagnostic Quiz and Score on Final Exam for 11
Students in Graduate Statistics
Diagnostic Quiz Final Exam Diagnostic Quiz Final Exam
32 36.50 84 75.25
60 49.75 84 103.00
60 36.75 92 108.00
76 61.75 92 89.25
84 92.25 100 91.50
84 61.00
c05.qxd 8/27/2004 2:53 PM Page 184
