Alfred DeMaris - Regression with Social Data, Modeling Continuous and Limited Response Variables

Подождите немного. Документ загружается.

which with 1 degree of freedom is, again, highly signiﬁcant (p  .00022). Apparently,

both tests result in a sound rejection of the null hypothesis of constant error variance.

WLS in Practice: Two-Step Procedure

To estimate the regression for coital frequency via WLS, we must ﬁrst estimate the

error variances. One possibility is to regress the squared OLS residuals from the sub-

stantive model on the model’s predictors and then to use the ﬁtted values from this run

as our estimates of σ

. The justiﬁcation for this is that the ﬁtted squared residuals are

consistent estimators of the expected squared residuals, which, as argued above, rep-

resent the error variances (McClendon, 1994). More generally, we regress the squared

residuals on a set of explanatory variables which may or may not coincide with the

substantive predictors, but which appear to determine the error variance (Greene,

2003). In the present case, I regressed the squared residuals on male’s age and the

square of male’s age—the same model as used for White’s test—and used the ﬁtted

values to create the weights. Failure to include the square of male age would result in

several cases having negative weights and therefore being excluded from the regres-

sion. In this case, including the quadratic term is an easy way to prevent that. (Below

I consider another technique for ensuring that the weights remain positive.) The

weights are then simply the reciprocals of the ﬁtted values. That is, I take w

 1/eˆ

the weights for the WLS regression. (Most regression software has an option for run-

ning weighted regression; in SAS, for example, one simply includes a WEIGHT

statement followed by the name of the weight variable.) The results are shown as the

last column of Table 6.1. The magnitudes of both intercept and slope have been

reduced slightly. The standard error of the slope has also been reduced, consistent with

the WLS estimator exhibiting lower variance compared to OLS. Nonetheless, sub-

stantive conclusions are little aﬀected by correcting for heteroscedasticity here.

for WLS. The R

for the OLS model is shown at the bottom of the ﬁrst column

of Table 6.1, suggesting that about 13% of the variation in coital frequency is

accounted for by male age. Two R

’s are shown for the WLS run in the last column.

The ﬁrst, R

OLS

, is the one reported by the software from the WLS analysis. It should

appear suspicious to the reader. Because the OLS estimators result in the smallest

SSE compared to any other estimators, they necessarily produce the highest R

in any

given sample. Therefore, the WLS estimates cannot result in a higher R

. The

“catch” is that the number reported by software is for the transformed (by the

weights) data, not the original data. To get the correct R

value, we need to “hand-

calculate” (with the aid of a computer) the ﬁtted values using the WLS estimates,

then use these ﬁtted values to construct the WLS residuals. We then sum the squared

WLS residuals to get SSE

, and then R

WLS

is calculated as

WLS

 1 



This value is also shown in the WLS column and is slightly smaller than R

OLS

,as

expected.

HETEROSCEDASTICITY AND WEIGHTED LEAST SQUARES 205

c06.qxd 8/27/2004 2:53 PM Page 205

Ensuring Positive Weights. Estimating the error variances by performing an OLS

regression on the squared residuals to get the ﬁtted values will not always work. Very

often, several of the ﬁtted values will be negative and there is no way to model that

problem away. A solution proposed by Wooldridge (2000) is to assume that the

squared errors are related to the model predictors via an exponential function. In par-

ticular, we suppose that the squared errors are related to the predictors via the fol-

lowing equation:

 σ

exp(δ

 δ



...

 δ

)u,

where u, the error term in this model, has mean 1 and is orthogonal to the predictors.

This is really no more arbitrary than the assumption that the squared error is linearly

related to the predictor set but has the additional advantage of ensuring that ε

always positive. The equation is then transformed so that it can be estimated via OLS:

log ε

 α

 δ



...

 δ

 υ, (6.1)

where α

 log σ

 δ

and υ  log u. According to Wooldridge, (6.1) now satisﬁes

the classic regression assumptions and we can therefore use OLS to get unbiased

estimates of its parameters. Using these, we obtain the ﬁtted values and then trans-

form them using the exponential function to get the estimated squared residuals for

the weights. In other words, the procedure is:

1. Run the regression of Y on X

, X

,...,X

and save the residuals, e

2. Create the variable log e

3. Regress log e

on X

, X

,...,X

and get the ﬁtted values, log eˆ

4. Exponentiate log eˆ

to recover eˆ

5. Regress Y on X

, X

,...,X

via WLS using as weights w

 1/eˆ

Coital Frequency Revisited. Table 6.2 presents results for the regression of coital

frequency on male age (in years), female age (in years), union duration (duration of

the union in years as of wave 1), couple modernism, and couple disagreement (inter-

val variable ranging from 1  “minimal disagreement” to 6  “maximum disagree-

ment”) for our 416 couples. The ﬁrst column is, again, the result of OLS estimation.

It appears that in addition to male age, couple modernism has a negative impact on

sexual activity. This is probably due to more modern couples being more gender

egalitarian. Such couples are likely to accord greater weight to the woman’s desires

regarding the frequency of sex, and women typically desire sex less often than men.

Net of other factors, the female’s age is also negatively related to coital activity, but

the eﬀect is not quite signiﬁcant.

As in the SLR model, I again suspect heteroscedasticity. This appears to be

conﬁrmed in Figure 6.2, which is a plot of the residuals against the ﬁtted values. The

ﬁgure reveals that the error variance appears to increase dramatically with increas-

ing values of predicted coital frequency. The White standard errors for the OLS run

206 ADVANCED ISSUES IN MULTIPLE REGRESSION

c06.qxd 8/27/2004 2:53 PM Page 206

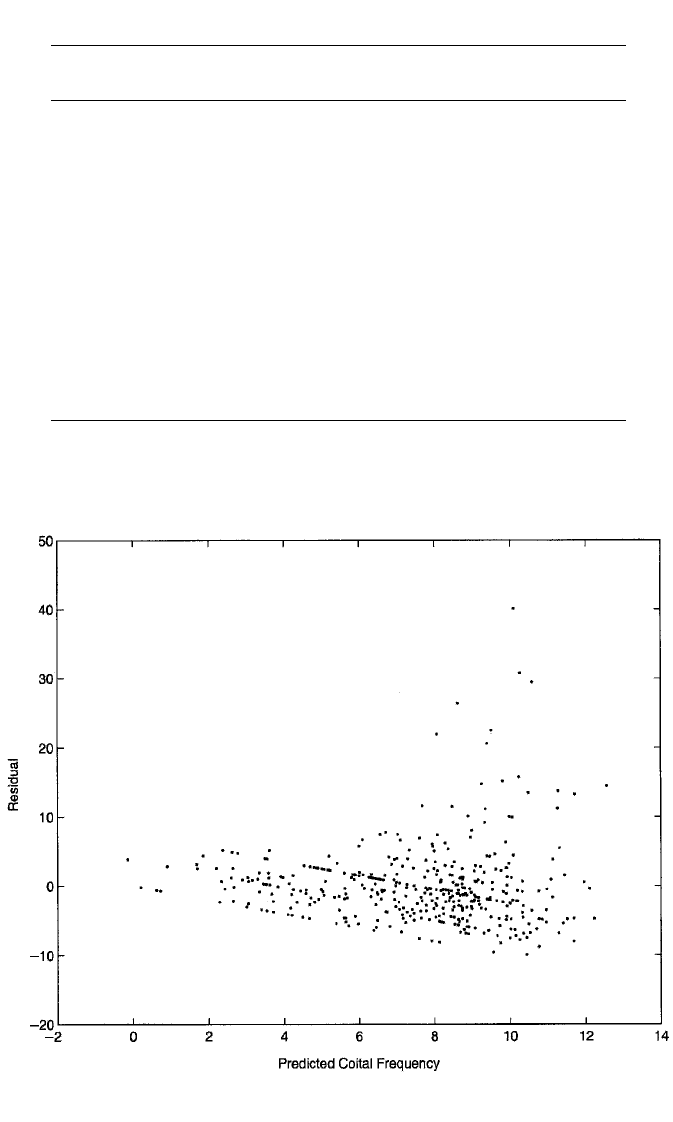
Table 6.2 OLS and WLS Results for the Multiple Regression of Coital

Frequency on Selected Predictors for 416 Couples in the NSFH

OLS: White Model for WLS:

Predictor b(σ

) σ

B-P Test

b(σ

)

Intercept 24.158*** 155.102* 19.433***

(3.723) (3.972) (3.147)

Male age .092* .815 .093**

(.040) (.028) (.030)

Female age .065 .405 .047

(.044) (.031) (.032)

Union duration .033 .397 .026

(.033) (.024) (.022)

Modernism .287* .2.482 .156

(.114) (.120) (.095)

Disagreement .958 .738 .791

(.513) (.528) (.441)

OLS

.1577 .0373 .2431

WLS

.1530

Response variable is the squared OLS residual.

* p  .05. ** p  .01. *** p  .001.

Figure 6.2 Scatterplot of residuals against ﬁtted values from the multiple regression of coital frequency

on selected predictors for 416 couples in the NSFH.

c06.qxd 8/27/2004 2:53 PM Page 207

are shown in the second column of Table 6.2. About half are larger than the OLS

standard errors and about half are smaller. Using the White standard errors, however,

the main substantive change would be that female age would become signiﬁcant at

p  .04. The model for the Breusch–Pagan test is shown in the third column of the

table. The test statistic value is 15.517 and is chi-squared with 5 degrees of freedom

under the null. With a p-value of .0084, we would reject homoscedasticity. White’s

test statistic (not shown), on the other hand, is 27.997 and has 20 degrees of free-

dom, a nonsigniﬁcant result (p  .1). Nonetheless, as the Breusch–Pagan test con-

centrates its power speciﬁcally on heteroscedasticity, it will be more trustworthy

here. The last column of the table shows the WLS analysis based on using equation

(6.1) to estimate the weights. Notice that all of the standard errors are smaller com-

pared to those from OLS, evidence again of the greater eﬃciency of WLS. However,

the only signiﬁcant predictor of coital frequency in the model is male age.

Testing Slope Homogeneity with WLS

In Chapter 3 I presented salary models for male and female faculty at BGSU and tested

whether they were the same. Although the test was signiﬁcant, suggesting that the

eﬀects of predictors on salary were diﬀerent across gender, a critical assumption for

this test—equal error variances across groups—was found in Chapter 4 to be violated.

As I indicated in Chapter 4, when the equal error variance assumption is violated, there

is a WLS procedure that still allows us to test regression slope homogeneity—or equal-

ity of predictor eﬀects—across groups. This approach is, however, restricted to having

only two groups. As outlined by Overton (2001), the idea is as follows. Suppose that

we have two groups in which the following models hold:



冱

 ε

,V(ε

)  σ



冱

 ε

,V(ε

)  σ

where the subscripts/superscripts 1 and 2 stand for groups 1 and 2, and σ

 σ

Suppose further that each group’s data are weighted by the reciprocals of their error

standard deviations. Then we have







冱





and







冱





In this case, the new error variances are

冢



冣





V(ε

) 



 1 and V

冢



冣





V(ε

) 



 1.

That is, the weighting procedure restores error-variance homogeneity across groups,

rendering tests for group-covariate interactions valid (Overton, 2001). It should be

208 ADVANCED ISSUES IN MULTIPLE REGRESSION

c06.qxd 8/27/2004 2:53 PM Page 208

noted that the case of unequal error variances across groups is not the same as het-

eroscedasticity, which is inequality of error variances across cases within groups. It

is still assumed in this procedure that the errors are homoscedastic within each group.

WLS in this case is used to correct only for unequal error variance across groups

(Overton, 2001).

To employ WLS to test slope homogeneity across two groups, we proceed as

follows:

1. Regress Y on the model’s main eﬀects separately in each of the two groups.

2. Compute MSE* SSE/(df

 2) separately for each group, based on each regres-

sion. The adjustment to the error degrees of freedom is necessary to correct for

the bias in the reciprocals of the error variances when used as weights (see

Overton, 2001, pp. 221–222).

3. Invert each MSE* to create each group’s weight.

4. Run WLS using the group weights in the combined sample, along with group-

covariate cross-product terms, to examine diﬀerences in predictor eﬀects across

groups.

Gender Diﬀerences in Salary Models, Revisited

Let’s tackle the issue of potential gender diﬀerences in the models for faculty salary one

more time. This time, having found that the error variances are unequal, I use the WLS

procedure outlined above. I employ the same model as in Table 3.5 except that this time

I omit the interaction of years at the university with years in rank. The basic model is

a regression of faculty salary on centered versions of prior experience, years in rank,

years at BG,and marketability. First I estimate the model separately for each gender

(results not shown). A test for error-variance homogeneity ( just to be sure that omitting

the interaction term doesn’t change things) results in an F of 1.527, which with 506 and

209 degrees of freedom, is again highly signiﬁcant (p  .001). I then create the weights

for each gender. For males, SSE/(df

 2)  41286268592/504  81917199.587. The

reciprocal of this is the males’ weight. For females SSE/(df

 2)  11166831326/

207  53946045.053. Its reciprocal is the females’ weight. I then reestimate the basic

model in the combined sample, weighting the cases diﬀerentially, according to gender.

The results of the WLS analysis are shown in Table 6.3.

Model 1 is the main eﬀects model. We see that the continuous covariates are all

signiﬁcant with the exception of years in rank. The dummy for being female is also

quite signiﬁcant and suggests that female salary is, on average, $4722.43 lower than

male salary. Model 2 adds the cross-products of female gender with the continuous

covariates. A nested F test, based on the R

’s from models 1 and 2 and reported at the

bottom of the model 2 column, suggests that the block of interaction terms is

signiﬁcant. This essentially agrees with the results of the Chow test reported in Chapter

3. Apparently this result is robust to correction for error variance heterogeneity. Two

of the individual cross-product terms are signiﬁcant. The more signiﬁcant interaction

eﬀect is that of female gender with prior experience. The eﬀect suggests that, for

males, each additional year of prior experience is worth a $1042.845 increment in

HETEROSCEDASTICITY AND WEIGHTED LEAST SQUARES 209

c06.qxd 8/27/2004 2:53 PM Page 209

academic-year salary. For females, each additional year is worth only 1042.845

 662.797  $380.048 in additional salary.

Overton (2001) notes that an advantage of the WLS procedure employed here is that

correct follow-up tests can be pursued to further explore the nature of the interaction

eﬀect. For example, given that the strongest interaction appears to be that between

female gender and prior experience, suppose that I wish to test whether the gender

diﬀerence in salary is signiﬁcant at diﬀerent levels of prior experience. A useful tech-

nique is to use the uncentered version of prior experience and rescale it as necessary to

isolate the diﬀerence coeﬃcient. (In Chapter 8 I refer to this scaling technique as tar-

geted centering and discuss it in more detail there.) In other words, the equation is:

yˆ  b

 d female  b

PE  b

years in rank  b

years at BG  b

marketability  g

female * PE. To begin, I let PE  prior experience. Then for those with no prior expe-

rience, PE  0. For males, estimated mean salary is yˆ  b

 b

years in rank  b

years

at BG  b

marketability. For females, it’s yˆ  b

 d  b

years in rank  b

years at

BG  b

marketability. The estimated diﬀerence in mean salary is d; therefore, a test for

the signiﬁcance of d is a test for gender diﬀerences in mean salary for those with no

experience. Okay, you already knew that. But suppose that we want to test gender

diﬀerences at two years of experience. Then we let PE  prior experience  2, and also

employ it for the cross-product term. For those with two years of experience, PE  0

again, and again, a test for d is a test for the gender diﬀerence in mean salary for those

with two years of experience. In general, to conduct the test of gender diﬀerence at c

years of experience, we estimate the model with PE  prior experience  c, form the

cross-product using this version of PE, and use the t test for d. Running this procedure

with c set alternately to 0, 2, and 10 years of prior experience produces the following

mean diﬀerences in female minus male average salary: 2885.81 (0 years), 4119.68

(2 years), and 9055.18 (10 years). All diﬀerences are highly signiﬁcant.

210 ADVANCED ISSUES IN MULTIPLE REGRESSION

Table 6.3 WLS Results for Testing Slope Homogeneity for Male vs.

Female Faculty in Eﬀects of Continuous Covariates on Salary for

725 Faculty Members

Predictor Model 1 Model 2

Intercept 49195.000*** 49036.000***

Female 4722.427*** 5213.543***

Prior experience

820.422*** 1042.845***

Years in rank

115.306 47.809

Years at BG

988.633*** 1009.120***

Marketability

31417.000*** 33601.000***

Female  prior experience

662.797***

Female  years in rank

447.862*

Female  years at BG

115.478

Female  marketability

7618.157

∆F 7.654***

Centered variable.

* p  .05. ** p  .01. *** p  .001.

c06.qxd 8/27/2004 2:53 PM Page 210

WLS with Sampling Weights: WOLS

A ﬁnal application of WLS that should be mentioned is the use of WLS for weight-

ing regression analyses with sampling weights. Sampling weights are typically pro-

vided with secondary data gathered from complex sampling designs. In such designs,

diﬀerent individuals have diﬀerent probabilities of selection into the sample, and the

weights are used to make the sample distributions on one’s variables resemble their

population counterparts. This is important for the estimation of univariate parame-

ters such as means and proportions. It is often thought that regression analyses

should also be weighted with sampling weights in order to achieve correct infer-

ences. Winship and Radbill (1994), however, explain why this is not an advisable

practice most of the time.

First, if the unweighted data are homoscedastic, sampling weights will make

them heteroscedastic. Why? Suppose that the correct model for the data is



冱

 ε

where ε

is normal with zero mean and variance σ

. However, we weight the data

before analysis, so that the data are actually

兹w

苶

 兹w

苶

冱

 兹w

苶

Now the variance of the errors is V(兹w

苶

)  w

, which of course implies het-

eroscedasticity. The immediate consequence of this is that as we have seen, standard

errors produced by regression software are no longer valid. Weighted estimators are

optimal and produce correct estimates of standard errors only when the weights are

a function of the error variances (Myers, 1986).

Second, if sampling weights are only a function of the independent variables

included in the model being estimated, unweighted OLS is really the appropriate

procedure. Using versus not using weights would be equivalent to drawing samples

exhibiting diﬀerent distributions on the X’s. Yet none of the classic regression

assumptions requires that the distributions of the X’s in the sample mirror those in

the population. In fact, if the model is speciﬁed correctly, samples exhibiting diﬀerent

distributions on the X’s should produce the same OLS estimates (Winship and Radbill,

1994). But if the model is misspeciﬁed, samples with diﬀerent X distributions may

very well produce diﬀerent regression estimates. So if the parameter estimates from

weighted and unweighted analyses diﬀer, this suggests either that the model is

misspeciﬁed or that the weights are a function of the dependent variable (Winship and

Radbill, 1994).

To assess whether weighted and unweighted analyses produce diﬀerent estimates,

Winship and Radbill (1994) recommend employing the test devised by DuMouchel

and Duncan (1983). Letting W represent the weight variable, the test is as follows.

First, we estimate the substantive model:

E(Y)  β



冱

. (6.2)

HETEROSCEDASTICITY AND WEIGHTED LEAST SQUARES 211

c06.qxd 8/27/2004 2:53 PM Page 211

Then we add the weight variable plus all interactions of the weight variable with the

model’s predictors:

E(Y)  β



冱

 δW 

冱

. (6.3)

Both analyses are done using OLS. The test is a nested F test of (6.2) versus (6.3). If

it is nonsigniﬁcant, weighted and unweighted analyses do not diﬀer and the analyst

should proceed with OLS. If the test is signiﬁcant, model (6.3) should be examined

more closely. If the weight variable itself has a signiﬁcant eﬀect, this suggests that the

weights are a function of X’s omitted from the model. If one or more WX interaction

terms is signﬁcant, there may be imporant interaction terms missing from the model.

The analyst may then be able to respecify the model and perform the test again. If the

diﬀerence between weighted and unweighted analyses is still signiﬁcant, the analyst

should then employ weighted regression using the sampling weights. In that case,

however, Winship and Radbill (1994) suggest employing White’s heteroscedasticity-

robust estimator of V(b) to obtain the standard errors of coeﬃcients.

Example. Table 6.4 presents weighted and unweighted analyses of data from wave

one of the NSFH on 7273 intimate couples (married as well as cohabiting unmarried).

212 ADVANCED ISSUES IN MULTIPLE REGRESSION

Table 6.4 OLS and WOLS Results for the Regression of Couple Disagreement

on Demographic Predictors for 7273 Couples in the NSFH

Predictor Model 1 Model 2 Model 3

Intercept 11.122*** 11.044*** 11.171***

Cohabiting couple .400* .094 .517*

Union duration .066*** .066*** .066***

Biological children 1.894*** 1.951*** 1.873***

Stepchildren 1.194*** 1.030*** 1.260***

Minority couple .109 .584** .043

Male education .001 .018 .006

Female education .007 .018 .003

Income-to-needs ratio .010 .002 .012

Case weight .063

Weight  cohabiting couple .631

Weight  union duration .000

Weight  biological children .060

Weight  stepchildren .215

Weight  minority couple .462**

Weight  male education .017

Weight  female education .009

Weight  income-to-needs ratio .007

RSS 17597.692 17773.178

Actual value is .0003.

* p  .05. ** p  .01. *** p  .001.

c06.qxd 8/27/2004 2:53 PM Page 212

The dependent variable is couple disagreement: the average of male and female part-

ners’ reports of how often the couple has a serious disagreement (interval variable

ranging from 6  “minimal disagreement” to 36  “maximum disagreement”). The

NSFH data are from a complex sampling design in which certain groups were over-

sampled: cohabitors, recently married couples, minorities, stepparent families, and

one-parent families. Model 1 presents the results from the unweighted regression.

Among the predictors are male and female education (in years of schooling com-

pleted) as well as the income-to-needs ratio (the ratio of household income to the

poverty level for that type of household). As the model also includes dummies for

cohabitation, being a minority couple, having only biological children,and having

stepchildren (the contrast is being childless), as well as the continuous covariate union

duration (in years), the sampling weights are functions of model predictors. We

would therefore expect that weighting would make no diﬀerence in the parameter

estimates. MSE for model 2 is 16.509. The last row of the table shows the RSS values

necessary to compute DuMouchel and Duncan’s (1983) test statistic, which is

F 1.181.

The p-value for this test statistic is greater than .3, suggesting that weighted and

unweighted analyses do not diﬀer. Model 3 presents the weighted estimates for com-

parison purposes. Clearly, there is no substantive diﬀerence between model 3 and

the OLS results. Although the nested F is nonsigniﬁcant, we notice that there is one

signiﬁcant interaction in model 2 between the weight variable and the dummy minor-

ity couple. If the DuMouchel and Duncan test had been signiﬁcant, this term might

suggest an omitted interaction. In previous analyses of these data, I did ﬁnd an inter-

action between minority status and the income-to-needs ratio in their eﬀects on couple

violence (DeMaris, 2003). I therefore checked to see if the same interaction eﬀect was

signiﬁcant for couple disagreement (results not shown), but it was not. In sum, the esti-

mates for model 1 would seem to represent the optimal estimates for these data.

OMITTED-VARIABLE BIAS IN A MULTIVARIABLE FRAMEWORK

In Chapter 3 I presented a relatively simpliﬁed explication of omitted-variable bias. In

this section I present a more general framework from which to understand this issue.

In the process I show that omitted variables can also confound, suppress, or mediate

the eﬀects of higher-order terms such as cross-products and quadratic eﬀects. First,

recall that an interaction eﬀect is of the form β

 γ

, where the subscripts j and

k refer to two diﬀerent predictors in the model. The eﬀect of X

is β

 γ

,which

shows that the eﬀect of X

depends on the level of X

. If γ

is zero, there is no interac-

tion and the eﬀect of X

is constant over levels of X

. Similarly, a quadratic eﬀect is of

the form β

 γ

. The eﬀect (partial derivative) of X

is β

 2γ

. If γ

is again

zero, there is no quadratic eﬀect and the relationship between Y and X

is linear. The

point is that the coeﬃcient of the cross-product term or the quadratic term represents

the departure from additivity or linearity, respectively. That is, the higher-order term is

(17773.178  17597.692)/9



16.509

OMITTED-VARIABLE BIAS IN A MULTIVARIABLE FRAMEWORK 213

c06.qxd 8/27/2004 2:53 PM Page 213

what “carries” the eﬀect in question. Hence, it is the association of this term with omit-

ted variables that may lead to bias.

Mathematics of Omitted-Variable Bias

To understand the eﬀect of variable omission, let’s suppose that the true model for Y

is y  X

ββ



εε

, with

εε

being normal with zero mean and variance σ

I. Let’s further

partition the X matrix as [X

], where the matrix X

consists of the variables that

the researcher includes in his or her model, and the matrix X

consists of vari-

ables left out of the researcher’s model. The corresponding partitioning of

ββ



[

ββ



ββ

 ], where

ββ

contains the parameters associated with X

and

ββ

those associ-

ated with X

. We further stipulate that X

has K variables, the ﬁrst being a column

of ones, and X

has Q variables. Similarly,

ββ

has K parameters, including the inter-

cept, and

ββ

has Q parameters. Without loss of generality I also assume that the Kth

variable in X

is a cross-product term of the form X

. Then y  X

ββ



εε

becomes

y  X

ββ

 X

ββ



εε

(in multiplying these partitioned entities we treat X like a row

vector). But instead, the researcher estimates y  X

ββ

 υ, where

υυ

 X

ββ



εε

What is the result?

The OLS estimator for the researcher’s model is

 (X

)

1

X

which, in actuality, is

 (X

)

1

X

ββ

 X

ββ



εε

]

 (X

)

1

X

ββ

 (X

)

1

X

ββ

 (X

)

1

X

εε



ββ

 (X

)

1

X

ββ

 (X

)

1

X

εε

which means that

E(b

) 

ββ

 (X

)

1

X

ββ

 (X

)

1

X

εε

) 

ββ

 (X

)

1

X

ββ

Hence, the term (X

)

1

X

ββ

represents the bias in b

due to the excluded regres-

sors (since, formally, the bias in b

is deﬁned as E(b



ββ

)  E(b

)

ββ

It is worthwhile to consider this bias in greater detail. The matrix (X

)

1

X

referred to as the alias matrix (Myers, 1986), represents the matrix of least squares

solutions for the regression of each of the predictors in X

on the set of regressors in

. Why? Let’s partition X

as [x

...

], adding a “2” subscript to the

column vectors to denote that these are the columns of X

. Then

(X

)

1

X

 (X

)

1

X

...

]

 [(X

)

1

X

(X

)

1

X

...

(X

)

1

X

]. (6.4)

It should be clear from (6.4) that each column of the K  Q alias matrix is a vector

of OLS coeﬃcients for the regression of a given column of X

(i.e., a given regressor

214 ADVANCED ISSUES IN MULTIPLE REGRESSION

c06.qxd 8/27/2004 2:53 PM Page 214