Alfred DeMaris - Regression with Social Data, Modeling Continuous and Limited Response Variables
Подождите немного. Документ загружается.


(c) yˆ 5 3.25x .15x
2
.
(d) yˆ 4 3x 1.25x
2
.
5.16 Suppose that the model for E(Y ) is E(Y ) 25 .25x .15x
2
3z, where X and
Z are centered and s
z
1.75. Give the value of E(Y) at the mean value of X and
Z, at the mean of X but Z at z
苶
1 s
z
, and at the mean of X but Z at z
苶
1 s
z
.
5.17 Suppose that the model for E(Y) is E(Y) 4 3x .25x
2
1.5z .15xz,
where X and Z are centered and s
z
1.75. Give the value of ∂[E(Y)]/∂X at z
苶
,
z
苶
1 s
z
, and z
苶
1 s
z
.
5.18 Suppose that the model for E(Y) is E(Y) 5 1.75x 3z .35xz, where X
and Z are centered and s
z
1.75. Give the value of ∂[E(Y)]/∂X at z
苶
, z
苶
1 s
z
,
and z
苶
1 s
z
.
5.19 Suppose that the model for E(Y) is E(Y) 15 3x .25x
2
2z .15xz
.25x
2
z, where X and Z are centered and s
z
1.75. Give the value of ∂[E(Y )]/
∂X at z
苶
, z
苶
1 s
z
, and z
苶
1 s
z
.
5.20 Suppose that the model for E(Y ) is E(Y ) 5.2 5x 3z .45x
2
.25z
2
.13xz .07xz
2
.15x
2
z .09x
2
z
2
, where X and Z are centered and
s
z
1.75. Give the value of ∂[E(Y)]/∂X at z
苶
, z
苶
1 s
z
, and z
苶
1 s
z
.
In Exercises 5.21 to 5.25, identify whether the equation for E(Y) is charac-
terized by (a) a linear vs. nonlinear model, (b) a linear vs. nonlinear effect of
X or Z (in the absence of any interaction effects only), and (c) a linear vs.
nonlinear interaction in each of X and Z.
5.21 E(Y) α β log x γ z δz log x.
5.22 E(Y) α βx γx
2
δx
3
φz
1/2
λxz
1/2
.
5.23 E(Y) log(α βx γz λxz).
5.24 E(Y) α β
x
γ
z
λ
xz
.
5.25 E(Y) α x
β
γz λz
2
φzx
β
.
EXERCISES 195
c05.qxd 8/27/2004 2:53 PM Page 195

196
Regression with Social Data: Modeling Continuous and Limited Response Variables,
By Alfred DeMaris
ISBN 0-471-22337-9 Copyright © 2004 John Wiley & Sons, Inc.
CHAPTER 6
Advanced Issues in Multiple
Regression
CHAPTER OVERVIEW
In this chapter I address a number of topics that are of a more advanced nature. Their
complexity is due primarily to the necessity to resort to matrix algebra for much of
their theoretical development. As matrix algebra may be foreign to many readers, this
is arguably the most difficult chapter in the book. For this reason, the reader is
strongly encouraged to read Section V of Appendix A before proceeding with this
chapter. A familiarity with the notation and major concepts of matrix algebra will be
extremely helpful for getting the most out of this material. On the other hand, those
uncomfortable with the matrix developments can simply skip them and attend only
to the “bottom line,” as expressed in equations such as (6.5), (6.11), and (6.12) and
accompanying discussions.
I begin by reviewing the matrix representation of the multiple regression model.
I then take up the topic of heteroscedasticity and weighted least squares (WLS) esti-
mation, the optimal estimation procedure when the homoscedasticity assumption
fails. Along with this I discuss the use of WLS in testing slope homogeneity across
groups when the assumption of equal error variance fails. I also consider the issue of
using weighted regression on data from complex sampling schemes, employing
WLS with sampling weights. This technique is referred to as weighted ordinary least
squares (WOLS) (Winship and Radbill, 1994). I then return to the issue of omitted-
variable bias, giving a formal development of the problem in the context of multiple
regression. I also give an example showing how omitted-variable bias can affect
interaction terms. The latter part of the chapter is devoted to regression diagnostics.
In particular, I explain how to diagnose regression analyses for undue influence
exerted by one or more observations. I also give a detailed explication of the problem
c06.qxd 8/27/2004 2:53 PM Page 196

of multicollinearity, its diagnosis, and possible remedies. The chapter ends by con-
sidering two techniques designed to improve on OLS estimates in the presence of
severe collinearity: ridge regression and principal components regression.
MULTIPLE REGRESSION IN MATRIX NOTATION
The Model
In Section V of Appendix A, I outline the matrix representation of the multiple regres-
sion model. Let’s review the basic concepts covered there. Recall that the matrix rep-
resentation of the model for the ith observation is y
i
x
i
ββ
ε
i
, where x
i
is a 1 p
vector of scores on the p regressors in the model for the ith observation. Here,
p K 1, and the first regressor score is a “1” that serves as the regressor for the
intercept term. Further,
ββ
is a p 1 vector of the parameters in the model, with the
first parameter being the intercept, β
0
. Y
i
and ε
i
are the ith response score and the ith
error term, as always. The matrix representation of the model for all n of the y scores
is y X
ββ
εε
. Here, y is an n 1 vector of response scores, X is an n p matrix of
the regressor scores for all n observations, and
εε
is an n 1 vector of equation errors
for the n observations. The ith row of X is, of course, x
i
. As always, it is assumed that
the errors have mean zero and constant variance σ
2
and are uncorrelated with each
other. These assumptions are encapsulated in the notation ε ⬃ f(0, σ
2
I). This means
that the errors have some density function, f(
.
) (typically assumed to be symmetric
about zero, but not necessarily normal except for small samples) with zero mean and
variance–covariance matrix σ
2
I. (Readers possibly used to the notation x
i
for the rep-
resentation of the vector of regressor scores for the ith case may find the notation x
i
used in this book to be somewhat unusual. However, in that the ith case’s regressor
values are contained in the ith row of the n p matrix of regressor values for all n
observations, and as I use the superscript i to denote row vectors, the use of x
i
seems
more appropriate. Note that the ith case’s collection of regressor values written as a
column vector is therefore denoted x
i
throughout the book.)
OLS Estimates
The vector of OLS estimates of the model parameters is denoted b, and as noted in
Appendix A, its solution is b (XX)
1
Xy. In Chapter 2 I noted that b
1
in SLR was
a weighted sum of the y
i
and therefore normally distributed in large samples, due to
the CLT. Similarly, each of the b
k
in the multiple regression model is a weighted
sum, or linear combination, of the y
i
and is therefore also asymptotically normal.
This is readily seen by denoting the p n matrix (XX)
1
X by the symbol G, and
its kth row (where k 0,1,...,K) as g
k
. Then the kth regression estimate has the
form g
k
y. Assuming that the X’s are fixed over repeated sampling (the standard
fixed-X assumption), this is nothing more than a weighted sum of the y’s. The esti-
mates are unbiased for their theoretical counterparts, since, as shown in Appendix A,
E(b)
ββ
. The variance–covariance matrix for b, denoted V(b), is σ
2
(XX)
1
. The
variances of the parameter estimates lie on the diagonal of this matrix.
MULTIPLE REGRESSION IN MATRIX NOTATION 197
c06.qxd 8/27/2004 2:53 PM Page 197

To illustrate the form of σ
2
(XX)
1
, let’s derive the expressions for the variances
of the SLR estimates, as given in Chapter 2, using matrix manipulations. In SLR, the
X matrix can be written [1x], where 1 is a vector of ones and x is the column vec-
tor of scores on the independent variable. Therefore, XX is
XX
冤冥
[1x]
冤冥
冤冥
.
The determinant of XX is
n冱x
2
冢冱x冣
2
n冱x
2
n
2
x
苶
2
n冢冱 x
2
nx
苶
2
冣 nS
xx
,
where S
xx
冱(x x
苶
)
2
[see Appendix A, Section II.C(1)]. The inverse of XX is,
therefore,
(XX)
1
nS
1
xx
冤冥
冤冥
Finally, σ
2
(XX)
1
is
σ
2
(XX)
1
冤冥
.
As the reader can see, the expressions for V(b
0
) and V(b
1
) on the diagonal of
σ
2
(XX)
1
are the same as given in Chapter 2.
Hat Matrix. The fitted values in regression, denoted yˆ
i
, are given by yˆ
i
x
i
b. The
vector of fitted values is therefore given by yˆ Xb. Substituting for b, we have
yˆ X(XX)
1
Xy, or yˆ Hy. H, equal to X(XX)
1
X, is called the hat matrix
(Belsley et al., 1980), since it converts y into yˆ. This matrix plays a key role in the
influence diagnostics discussed later in the chapter. Of particular interest are the
diagonals of this matrix, denoted h
ii
. These tap into the leverage, or potential for
influence, exerted on the regression estimates by the ith observation. The matrix for-
mula for h
ii
is h
ii
x
i
(XX)
1
x
i
.
Regression Model in Standardized Form
Recall from Chapter 2 that the standardized slope in SLR results from the OLS
regression of the standardized version of y on the standardized version of X. The
same holds true in multiple regression. However, to understand the standardized rep-
resentation of the MULR model, we must first examine the matrix representation of
the standardized variable scores. Suppose that we denote by y
z
the n 1 vector of
n
σ
S
2
x
冱
x
x
S
σ
x
2
x
σ
n
2
S
冱
x
x
x
2
n
σ
S
2
x
冱
x
x
nS
冱
xx
x
S
1
xx
n
冱
S
x
xx
nS
冱
xx
x
冱
x
n
冱
x
2
冱
x
冱
x
冱
x
2
n
冱
x
1x
xx
11
x1
1
x
198 ADVANCED ISSUES IN MULTIPLE REGRESSION
c06.qxd 8/27/2004 2:53 PM Page 198

standardized y-scores and by Z the n K matrix of standardized X scores (the “1”
disappears from this matrix in the standardization process; the standardized equation
therefore has no intercept). Now, note that (1/n)ZZ R
xx
, the correlation matrix for
the X’s, and (1/n)Zy
z
r
xy
, the vector of correlations between the X’s and y. Why?
First, understand that the ith element in the kth column of Z is of the form
z
ik
x
ik
s
k
x
苶
k
,
where s
k
is the standard deviation of the kth regressor. That is, the ikth element of Z
is the kth variable minus its mean divided by its standard deviation for the ith case.
Partitioning Z by its columns, ZZ is
ZZ
冤
冥
[z
1
...
z
K
]
冤
冥
.
This is a K K matrix whose kth diagonal element is
z
k
z
k
冱
(x
ik
s
2
k
x
苶
k
)
2
,
and whose off-diagonal elements are of the form
z
k
z
l
冱
(x
ik
s
x
苶
k
k
s
)
l
(x
il
x
苶
l
)
,
where k and l denote two different regressors in the model. Multiplying this matrix
by 1/n results in the kth diagonal element being of the form
冱
(x
ik
s
2
k
x
苶
k
)
2
/n
1,
and the off-diagonal elements being of the form
冱
(x
ik
x
苶
s
k
k
)
s
(
l
x
il
x
苶
l
)/n
r
kl
.
That is, the result is the correlation matrix for the X’s in the model. [Technically, we
should be multiplying by 1/(n 1) instead of 1/n, but asymptotically these are equiv-
alent, and 1/n simplifies the expression. It should be evident that the difference
between n 1 and n is virtually nil in large samples.] A similar argument demon-
strates that (1/n)Zy
z
r
xy
.
z
1
z
K
.
.
.
z
K
z
K
...
...
...
...
...
z
1
z
1
.
.
.
z
K
z
1
z
1
.
.
.
z
K
MULTIPLE REGRESSION IN MATRIX NOTATION 199
c06.qxd 8/27/2004 2:53 PM Page 199

To write the model in standardized form, we shall find it convenient to transform
the response and regressors as follows. Let X* (1/兹n
苶
)Z and y* (1/兹n
苶
)y
z
.
Myers (1986, p. 76) refers to y* and X* as the vector and matrix, respectively, of
centered and scaled variables. That is, the kth column of X*, for example, represents
a variable of the form
兹冱
苶苶
n
i
苶
x
i
1
k
(
苶
x
i
苶
x
k
苶
苶
k
x
k
苶
苶
)
2
苶
.
.
The vector y* represents Y in similar form. Then the standardized version of the model
is y* X*
ββ
s
εε
*
, and the standardized estimates are obtained via the OLS solution:
b
s
(X*X*)
1
X*y*
冤冢
兹
1
n
苶
Z
冣
冢
兹
1
n
苶
Z
冣冥
1
冢
兹
1
n
苶
Z
冣
兹
1
n
苶
y
z
冢
1
n
ZZ
冣
1
1
n
Zy
z
R
1
xx
r
xy
.
In other words, the standardized regression coefficients are the product of the inverse
of the correlation matrix for the X’s times the correlations of the X’s with y. Further,
letting σ
2
*
represent V(ε*), we then denote the variance–covariance matrix of the
errors in the standardized equation by σ
2
*
I. Then the variance–covariance matrix of
standardized parameter estimates is V(b
s
) σ
2
*
(X
*
X
*
)
1
σ
2
*
R
1
xx
. Having estab-
lished the matrix representations for key elements in the MULR model, we are now
ready to consider additional MULR topics.
HETEROSCEDASTICITY AND WEIGHTED LEAST SQUARES
Until now the standard assumption we have been operating under is that the equation
errors are homoscedastic; that is, they have constant variance at each covariate pat-
tern. In that case, V(
εε
) σ
2
I. Suppose that this isn’t the case. That is, suppose that the
error variances vary across covariate patterns such that V(ε
i
) σ
2
i
for i 1,2,...,n.
Assuming that the errors are still uncorrelated, the form of V(
εε
) is now
冤冥
V.
Under this scenario the appropriate estimator is the generalized least squares (GLS)
estimator, given by b
w
(XV
1
X)
1
XV
1
y (Myers, 1986). If V σ
2
I, b
w
is sim-
ply b, the OLS estimator. Because V is diagonal, and taking the inverse of a diago-
nal matrix is accomplished by simply inverting the diagonal elements, b
w
has the
form
b
w
(XD
w
i
X)
1
XD
w
i
y,
σ
2
1
0
...
0
0 σ
2
2
... .
. ... ... .
. ... ...
0
0
...
0 σ
2
n
200 ADVANCED ISSUES IN MULTIPLE REGRESSION
c06.qxd 8/27/2004 2:53 PM Page 200

where D
w
i
indicates a diagonal matrix with diagonal entries w
i
1/σ
2
i
. Now, if we
regard b
w
more closely, we see that it can be expressed as
b
w
[(
D
兹w
苶
i
苶
X
)
(
D
兹w
苶
i
苶
X
)]
1
(
D
兹w
苶
i
苶
X
)
D
兹w
苶
i
苶
y.
Recall that premultiplying a matrix or vector by a diagonal matrix simply multiplies
each row of that matrix or vector by the diagonal elements. Therefore, the design
matrix now has the form
D
兹w
苶
i
苶
X
D
兹w
苶
i
苶
[1x
1
...
x
K
]
冤冥
X
w
,
and the response vector has the form
D
兹w
苶
i
苶
y
冋册
y
w
.
If we regress y
w
on X
w
using OLS, the resulting estimator, (X
w
X
w
)
1
X
w
y
w
, will be
b
w
(as the reader can verify by substituting for X
w
and y
w
in this expression). What
this means is that b
w
can be found by transforming the regressors and the response
and then performing OLS on the transformed variables. The transformation involves
multiplying the regressors and the response by the square root of the weight vari-
able, where the weights are the reciprocals of the error variances. Hence this esti-
mator is called the weighted least squares (WLS) estimator. Notice that the first
column of the transformed design matrix is no longer a column of ones. Instead, it
is a column of weights, which constitutes another variable. Consequently, the appro-
priate OLS regression analysis is a regression through the origin. The constant term
for the WLS analysis is the coefficient for the weight variable resulting from this run
(McClendon, 1994).
Properties of the WLS Estimator
If the proper weights, 1/σ
2
i
, are known, the WLS estimator b
w
has the following prop-
erties: (1) it is unbiased for
ββ
; (2) it achieves the minimum variance of all linear unbi-
ased estimators; and (3) it is the MLE for
ββ
if the errors are also normally distributed
(Myers, 1986). Unfortunately, the true error variances are typically unavailable, so the
proper weights are rarely known in practice. In this case, the error variances must first
be estimated from the data available and then used in the weighting procedure. The
resulting WLS estimator, also known as the feasible generalized least squares (FGLS)
兹w
苶
1
苶
y
1
兹w
苶
2
苶
y
2
兹w
苶
n
苶
y
n
兹w
苶
1
苶
x
1K
兹w
苶
2
苶
x
2K
兹w
苶
n
苶
x
nK
...
...
...
...
...
兹w
苶
1
苶
x
11
兹w
苶
2
苶
x
21
兹w
苶
n
苶
x
n1
兹w
苶
1
苶
兹w
苶
2
苶
兹w
苶
n
苶
HETEROSCEDASTICITY AND WEIGHTED LEAST SQUARES 201
c06.qxd 8/27/2004 2:53 PM Page 201

estimator, is no longer unbiased; however, it is still consistent and has a smaller sam-
pling variance than that of the OLS estimator in large samples (Wooldridge, 2000).
Consequences of Heteroscedasticity
What are the consequences of using OLS in the presence of heteroscedasticity? First,
the OLS estimators are inefficient. That is, there exist estimators with a smaller sam-
pling variance: namely, the WLS (i.e., FGLS) estimator. This means that tests of
significance will typically be more sensitive when using WLS than when using OLS.
Perhaps more important, however, the estimated standard errors of the OLS coefficients
obtained via the formula σ
ˆ
2
(XX)
1
(the formula employed by all regression software)
are no longer valid under heteroscedasticity. To see why, recall from Appendix A that
for the OLS b,
V(b) V[(XX)
1
Xy] (XX)
1
XV(y)X(XX)
1
.
As long as V(y) σ
2
I, this matrix reduces to σ
2
(XX)
1
and then σ
ˆ
2
(XX)
1
becomes
an unbiased estimator of V(b). However, when heteroscedasticity prevails, V(y) V
(shown above). The variance of b is then
V(b) V[(XX)
1
Xy] (XX)
1
XVX(XX)
1
.
Hence, σ
ˆ
2
(XX)
1
is no longer a valid estimator of this variance–covariance matrix.
White’s Estimator of V(b). An alternative estimator of V(b) which is robust to het-
eroscedasticity is the White estimator (White, 1980). This is based on the idea that
the OLS b is a consistent estimator of
ββ
, which implies that the OLS residuals are
“pointwise consistent estimators” (Greene, 2003, p. 198) of the population ε
i
.
Moreover, the squared residuals would be consistent estimators of the squared ε
i
,
whose average values represent the variances of the ε
i
, since V(ε
i
) E(ε
i
E(ε
i
))
2
E(ε
2
i
). Assuming at least one continuous predictor, the squared error for each case
would typically be unique, so it represents its own average. Hence, the squared OLS
residuals can be used to estimate the error variances in V, leading to the White het-
eroscedasticity-robust estimator,
V
w
(b) (XX)
1
XV
ˆ
X(XX)
1
,
where V
ˆ
is a diagonal matrix containing the squared OLS residuals (White, 1980).
Testing for Heteroscedasticity
In this section I discuss two tests for heteroscedasticity that are relatively easy to
implement in any regression software that makes the residuals available for further
manipulation. These tests are also available on request in some software (e.g., STATA,
LIMDEP). The null hypothesis for either test is that the errors are homoscedastic. The
202 ADVANCED ISSUES IN MULTIPLE REGRESSION
c06.qxd 8/27/2004 2:53 PM Page 202

first is White’s test (White, 1980). For the substantive model E(Y) β
0
β
1
X
1
β
2
X
2
...
β
K
X
K
, the test is accomplished by first estimating the model with OLS
and then saving the residuals. One then regresses the squares of the residuals on all pre-
dictors in the model plus all nonredundant crossproducts among the predictors. For
example, if the model is E(Y) β
0
β
1
X
1
β
2
X
2
β
3
X
3
, one regresses the squared
residuals from estimating this model on X
1
, X
2
, X
3
, X
2
1
, X
2
2
, X
2
3
, X
1
X
2
, X
1
X
3
, and X
2
X
3
.
The test is then nR
2
from this run, which, under the null hypothesis of homoscedastic-
ity, is distributed as chi-squared with degrees of freedom equal to the number of regres-
sors used to model the squared residuals (in this case, that would be 9). Be advised,
however, that more than just homoscedasticity is being tested with this statistic. In fact,
White (1980, p. 823) describes this test as follows: “. . . the null hypothesis maintains
not only that the errors are homoskedastic, but also that they are independent of the
regressors, and that the model is correctly specified... .”In other words, this is more
of a general test for model misspecification.
The second test is the Breusch–Pagan test (Breusch and Pagan, 1979). This test
is much more focused on heteroscedasticity than White’s test, and, in fact, assumes
that the error variance is related in some systematic fashion to the model predictors
(Greene, 2003). There are various forms of the test, but the one I advocate here is
that suggested by Wooldridge (2000). In this case, one regresses the squared OLS
residuals from one’s substantitve model on just the predictors in one’s substantive
model. Once again, the test is nR
2
from this regression, which is distributed as chi-
squared with K degrees of freedom under the null hypothesis of homoscedasticity.
Example: Regression of Coital Frequency
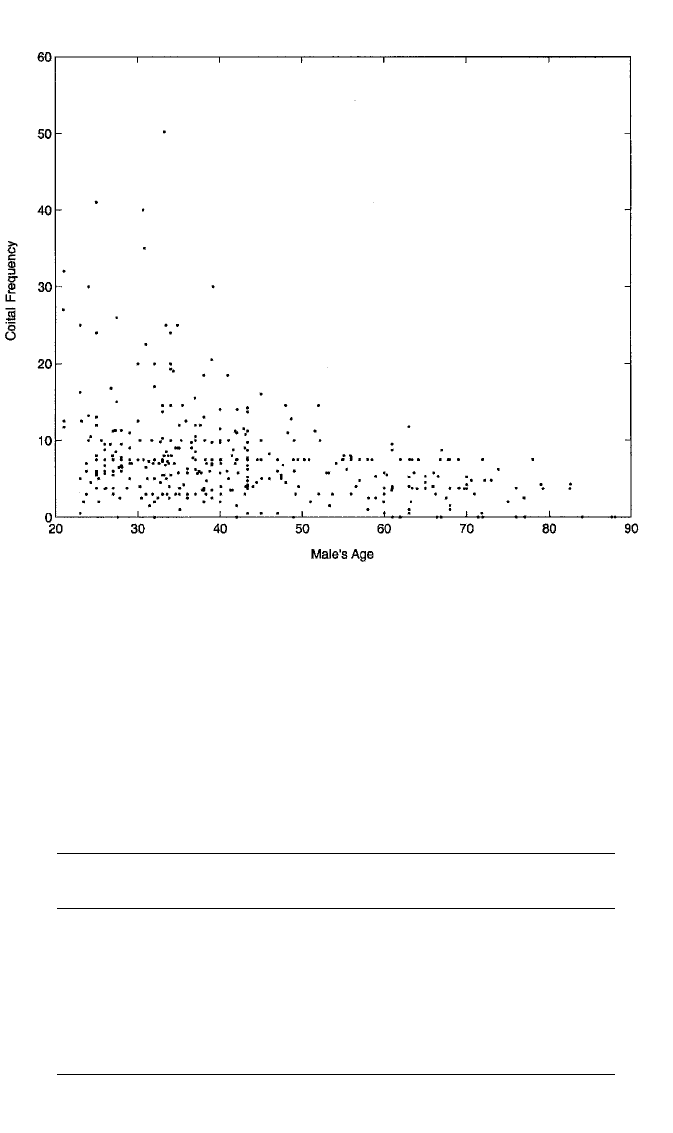
Let’s consider an example of a heteroscedastic model. Figure 6.1 presents a scatter-
plot of coital frequency in the last month against the male partner’s age for the 416
couples in the couples dataset. (This is similar to Figure 2.7, which shows a plot of
the residuals from this regression against male partner’s age.) Nonconstant error
variance is suggested by the wedge-shaped trend in the points in which the spread of
points tapers down dramatically from left to right. This phenomenon makes sub-
stantive sense. One would expect that there would be considerable variability in
coital frequency among young couples, since some are by choice more sexually
active than others. However, age brings its own limitations to sexual activity, regard-
less of individual proclivities. We would therefore expect less variability in sexual
frequency as couples enter middle and old age.
Table 6.1 presents regression results for these data. The first column shows the OLS
results for the regression of coital frequency on male’s age. The effect of male’s age is
negative and significant and suggests that each additional year of age reduces the cou-
ple’s coital frequency by about .15 time per month. The effect is quite significant. The
second column shows the standard errors estimated by White’s heterscedasticity-robust
technique. Compared to the OLS standard errors, the White standard errors are larger
for the intercept but slightly smaller for the effect of age. No real substantive difference
would result from using these standard errors in place of the OLS ones, however. The
third column presents the model for White’s test, which includes both male age and its
HETEROSCEDASTICITY AND WEIGHTED LEAST SQUARES 203
c06.qxd 8/27/2004 2:53 PM Page 203
square. The dependent variable for this run is the squared residual from the model in
the first column. White’s test is therefore 416(.0423) 17.597. With 2 degrees of free-
dom, this is quite significant (p .00015). For the Breusch–Pagan test, we regress the
squared residuals from the substantive model on male’s age (results not shown). The
R
2
from this run is .0328. Hence, the Breusch–Pagan test is 416(.0328) 13.645,
204 ADVANCED ISSUES IN MULTIPLE REGRESSION
Figure 6.1 Scatterplot of coital frequency with male’s age for 416 couples in the NSFH.
Table 6.1 OLS and WLS Results for the Regression of Coital
Frequency on Male Age for 416 Couples in the NSFH
OLS: White Model for WLS:
Predictor b(σ
ˆ
b
) σ
ˆ
b
White’s Test
a
b(σ
ˆ
b
)
Intercept 14.028*** 201.057*** 13.522***
(.874) (.998) (.992)
Male age .149*** 6.234** .143***
(.019) (.018) (.016)
(Male age)
2
.049*
R
2
OLS
.1295 .0423 .1570
R
2
WLS
.1280
a
Response variable is the squared OLS residual.
* p .05. ** p .01. *** p .001.
c06.qxd 8/27/2004 2:53 PM Page 204
