Alfred DeMaris - Regression with Social Data, Modeling Continuous and Limited Response Variables
Подождите немного. Документ загружается.


dependence. Hence, a near-zero eigenvalue of X*X* is indicative of near linear
dependence among the regressors. This is easier to see if we take advantage of the
eigenvalue decomposition of X*X*:
U(X*X*)U
冤冥
(X*X*)[u
1
u
2
...
u
K
]
冤冥
冤冥
.
Now, if one of the eigenvalues, say λ
K
, is near zero, we have that
u
K
(X*X*)u
K
(X*u
K
)(X*u
K
) 艐 0.
Notice that since X*u
K
is a vector (its dimensions are K 1), (X*u
K
)(X*u
K
) is
essentially the sum of squares of all elements of X*u
K
. And the sum of squares of
all elements can be near zero only if the vector itself is approximately the zero vec-
tor. In that X*u
K
is a linear combination of the columns of X*, this implies that the
columns of X* are approximately linearly dependent, according to the definition of
linear dependence given above. Moreover, the elements of u
K
reveal the nature of the
dependency, since they indicate the weights for the linear combination of the
columns of X* that is approximately zero.
For example, Dunteman (1989) presents a regression, for 58 countries, of educa-
tional expenditures as a percent of the gross national product (Y) on six characteris-
tics of countries: population size (X
1
), population density (X
2
), literacy rate (X
3
),
energy consumption per capita (X
4
), gross national product per capita (X
5
), and elec-
toral irregularity score (X
6
). The spectral decomposition of the design matrix reveals
one relatively small eigenvalue of .047, with the following associated eigenvector:
0
0
λ
K
0
0
λ
2
λ
1
0
0
u
1
(X*X*)u
K
u
K
(X*X*)u
K
u
1
(X*X*)u
2
u
2
(X*X*)u
2
u
K
(X*X*)u
1
u
1
(X*X*)u
1
u
2
(X*X*)u
1
u
K
(X*X*)u
1
u
1
u
2
u
K
REGRESSION DIAGNOSTICS II: MULTICOLLINEARITY 225
c06.qxd 8/27/2004 2:53 PM Page 225

u (.005 .097 .065 .660 .729 .152). The largest weights are for X
4
and X
5
, suggesting that these two variables are somewhat linearly dependent. Ignoring
the other elements of this vector, we have .660X
4
.729X
5
⬇0, or X
4
⬇1.105X
5
. In
fact, the correlation between these two regressors is .93.
Consequences of Collinearity
In Chapter 3 I suggested that two major consequences of multicollinearity were an
inflation in the variances of OLS estimates and an inflation in the magnitudes of the
coefficients themselves. To understand how collinearity causes these problems, we
rely once again on the spectral decomposition of X*X*. First, consider the matrix
expression for the sum of the variances of the standardized coefficients. We begin
with the expression (b
s
ββ
s
)(b
s
ββ
s
):
(b
s
ββ
s
)(b
s
ββ
s
) [b
s
1
β
s
1
b
s
2
β
s
2
... b
s
K
β
s
K
]
冤冥
冱
冢b
s
k
β
s
k
冣
2
,
and therefore,
E[(b
s
ββ
s
)(b
s
ββ
s
)]
冱
E(b
s
k
β
s
k
)
2
冱
V(b
s
k
),
this last term being the sum of the variances of the standardized coefficients. Now
the variances of the coefficients are on the diagonal of the matrix σ
2
*
(X*X*)
1
. The
sum of the diagonal elements of this matrix is, of course, its trace, and the trace of a
square matrix is the sum of its eigenvalues. Moreover, the eigenvalues of the inverse
of a matrix are simply the reciprocals of the eigenvalues of the matrix itself (the
proof of this is left as an exercise for the reader). Therefore, the eigenvalues of
(X*X*)
1
are simply of the form 1/λ
k
. Thus,
冱
V(b
s
k
) tr[σ
2
*
(X*X*)
1
] σ
2
*
tr[(X*X*)
1
]
冱
K
i1
σ
λ
2
*
i
, (6.11)
and since
E[(b
s
ββ
s
)(b
s
ββ
s
)]
冱
V(b
s
k
)
冱
K
i1
σ
λ
2
*
i
,
we have that
E[b
s
b
s
b
s
ββ
s
ββ
s
b
s
ββ
s
ββ
s
]
冱
K
i1
σ
λ
2
*
i
,
or
E(b
s
b
s
) E(b
s
)
ββ
s
ββ
s
E(b
s
)
ββ
s
ββ
s
冱
K
i1
σ
λ
2
*
i
,
b
s
1
β
s
1
b
s
2
β
s
2
b
s
K
β
s
K
226 ADVANCED ISSUES IN MULTIPLE REGRESSION
c06.qxd 8/27/2004 2:53 PM Page 226

or
E(b
s
b
s
)
ββ
s
ββ
s
冱
K
i1
σ
λ
2
*
i
. (6.12)
Equation (6.12) shows that the sums of squares of the coefficient estimates are heav-
ily upwardly biased when there is multicollinearity, as indexed by one or more small
eigenvalues. This means that the coefficients will have a tendency to be too large in
magnitude if the regressors are collinear (Myers, 1986).
Why are the coefficient variances inflated? The spectral decomposition of
(X*X*)
1
is
(X*X*)
1
冱
K
i1
λ
1
i
u
i
u
i
λ
1
1
u
1
u
1
λ
1
2
u
2
u
2
...
λ
1
K
u
K
u
K
. (6.13)
Now, to simplify things somewhat, let’s consider what this matrix looks like for three
regressors, focusing only on the diagonal elements. In this case (X*X*)
1
is
λ
1
1
冤冥
[u
11
u
21
u
31
]
λ
1
2
冤冥
[u
12
u
22
u
32
]
λ
1
3
冤冥
[u
13
u
23
u
33
]
冤冥
冤冥
冤
冥
冤冥
.
The diagonals of σ
∗
2
(X*X*)
1
represent the coefficient variances. So, for example,
the variance of b
1
s
is then equal to
σ
∗
2
冢
u
λ
2
1
1
1
u
λ
2
1
2
2
u
λ
2
1
3
3
冣
. (6.14)
This expression should make it clear that collinearity, in the form of a small eigen-
value, will tend to inflate the variance of a given coefficient. In fact, a given near lin-
ear dependency has the potential to affect the variances of all of the coefficients; but
u
λ
2
1
1
1
u
λ
2
1
2
2
u
λ
2
1
3
3
u
λ
2
2
1
1
u
λ
2
2
2
2
u
λ
2
2
3
3
u
λ
2
3
1
1
u
λ
2
3
2
2
u
λ
2
3
3
3
u
λ
2
1
3
3
u
λ
2
2
3
3
u
λ
2
3
3
3
u
λ
2
1
2
2
u
λ
2
2
2
2
u
λ
2
3
2
2
u
λ
2
1
1
1
u
λ
2
2
1
1
u
λ
2
3
1
1
u
13
u
23
u
33
u
12
u
22
u
32
u
11
u
21
u
31
REGRESSION DIAGNOSTICS II: MULTICOLLINEARITY 227
c06.qxd 8/27/2004 2:53 PM Page 227

there is a “catch.” Suppose that X
2
and X
3
are highly correlated but both are close to
orthogonal to X
1
. Then most likely λ
3
will be fairly small, but so will u
13
, since the
high-magnitude weights will be u
23
and u
33
. In this case, the contribution to V(b
1
s
) of
the last term inside the parentheses will be negligible. This suggests that the vari-
ables responsible for the near linear dependencies in the data are the ones whose
variances are primarily affected by collinearity.
Diagnosing Collinearity
There are three major tools in the diagnosis of collinearity. Expression (6.14) is associ-
ated with two of them. The first is the VIF, introduced in Chapter 3. The VIF tells us
how many times the variance of a coefficient is magnified as a result of the collinearity
compared to the ideal case of perfectly orthogonal regressors (Myers, 1986). It turns
out that the VIF’s are the diagonal elements of R
xx
1
(Neter et al., 1985); hence, the term
inside the parentheses in (6.14) is the VIF for b
1
s
(or for b
1
, since the VIF is the same for
the unstandardized coefficient as it is for the standardized one). As mentioned previ-
ously, VIF’s of about 10 or higher indicate collinearity problems. The second diagnos-
tic allows us to discern which variables are, in fact, approximately linearly dependent.
This is the variance proportion, or p
ji
:
p
ji
σ
V
*
2
u
(b
ij
2
i
s
/
)
λ
j
.
This is interpreted as the proportion of the variance of b
i
attributable to the collinear-
ity characterized by λ
j
. For example, from (6.14) we have
p
31
σ
*
V
2
u
(
1
b
3
2
1
s
/
)
λ
3
.
Typically, high variance proportions associated with the same eigenvalue for two or
more regressors indicate that those regressors are approximately linearly dependent.
The third useful diagnostic is called the condition number of the (X*X*)
1
matrix.
It is the ratio of the largest to the smallest eigenvalue and is typically symbolized by
φ. Condition numbers greater than 1000 are indicative of collinearity problems in the
matrix. Often, what is reported as the condition number by software (e.g., SAS) is
the square root of φ, in which case the cutoff is about 32. According to Myers (1986),
a complete collinearity diagnosis uses the condition number to assess the seriousness
of linear dependencies in the design matrix, the variance proportions to identify
which variables are involved, and the VIF’s to determine the amount of “damage” to
individual coefficients.
Illustration
Table 6.7 presents collinearity diagnostics for data reported in Neter et al. (1985) on
20 healthy females aged 25–34. The response variable is body fat, while the regres-
sors are triceps skinfold thickness (X
1
), thigh circumference (X
2
), and midarm cir-
cumference (X
3
). Although not exactly typical “social” data, this example was chosen
228 ADVANCED ISSUES IN MULTIPLE REGRESSION
c06.qxd 8/27/2004 2:53 PM Page 228

primarily because it illustrates the symptoms and warning signs of extremely collinear
data. The OLS regression of body fat on the three independent variables is shown in
the first column of panel A of the table. A couple of symptoms of collinearity are
already evident here. To begin, the sign of the coefficient for thigh circumference is
counterintuitive: We would expect a greater thigh circumference to predict more, not
less, body fat. Also, the standardized coefficients are outside the range [ 1, 1]. The
VIF’s confirm that there is a collinearity problem that affects all of the coefficients:
All VIF’s are well over 10—by a factor of at least 10!
Panel B shows the eigenvalues of the XX matrix as well as its condition num-
bers (i.e., 兹φ
苶
for the ratio of the largest eigenvalue to each successively smaller one)
and the variance proportions. In this case, we are using the decomposition of XX
instead of X*X*. Either matrix is useful for diagnosing collinearity, although Myers
(1986) recommends using X*X* if the intercept is not of special interest. At any
rate, the smallest eigenvalue is associated with a condition number of 677.372.
Bearing in mind that 32 is the cutoff, this is quite large indeed. This suggests that
there is a serious linear dependency in the matrix. The variance proportions indicate
that all three regressors, as well as the intercept, are tied together in a near linear
dependency.
A somewhat more realistic example, at least by social science criteria, is shown
in Table 6.8, which presents collinearity diagnostics for a regression using the NSFH
data employed for Table 6.4. This time I regress couple disagreement on several con-
trols plus the variables current male- and female age, male- and female age at the
beginning of the union, (shown simply as male- and female “age at union” in the
REGRESSION DIAGNOSTICS II: MULTICOLLINEARITY 229
Table 6.7 OLS, Ridge, and Principal Components Regression Results, and
Collinearity Diagnostics for Body Fat Data from 20 Women
Panel A: Regression Results
OLS Ridge PC
Predictor Estimator b
s
VIF Estimator Estimator
Intercept 117.085 7.403 12.205
Triceps skinfold thickness 4.334 4.264 708.843 .555 .422
Thigh circumference 2.857 2.929 564.343 .368 .492
Midarm circumference 2.186 1.561 104.606 .192 .125
R
2
.801***
Panel B: Collinearity Diagnostics
Variance Proportions
λ No. λ Value 兹φ
苶
p
j0
p
j1
p
j2
p
j3
1 3.968 1.000 .0000 .0000 .0000 .0000
2 .021 13.905 .0004 .0013 .0000 .0014
3 .012 18.566 .0006 .0002 .0003 .0069
4 .000009 677.372 .9990 .9985 .9996 .9917
*** p .001.
c06.qxd 8/27/2004 2:53 PM Page 229

table), and union duration. In a complete dataset with no missing values, these vari-
ables would be exactly linearly dependent since current age age at union union
duration. However, it is typical in survey data that answers are not recorded for a
number of cases. In this instance, I used mean substitution for the missing data.
Filling in the missing data with imputed values nullifies the exact linear dependency,
making it possible to estimate a regression. Again, the first column of panel A shows
the OLS results. This time none of the standardized coefficients is outside the range
[ 1, 1]. However, although the coefficient is not significant, the sign of the effect of
female age is somewhat counterintutive, since older couples typically have fewer
disagreements. The VIF’s suggest that at least three of the coefficient variances are
affected by collinearity: those for male age, female age, and union duration. The
coefficients for male- and female age at the beginning of the union have variances
that are somewhat inflated, but not by enough to cause concern.
Panel B again shows condition numbers and variance proportions. However,
this time I have only shown diagnostics connected with the two smallest eigenval-
ues. The smallest eigenvalues are associated with condition numbers of 31.197
and 41.329, which are just large enough to signal that there are some approximate
230 ADVANCED ISSUES IN MULTIPLE REGRESSION
Table 6.8 OLS, Ridge, and Principal Component Regression Results, and
Collinearity Diagnostics for Regression of Couple Disagreement on Demographic
Predictors for 7273 Couples in the NSFH
Panel A: Regression Results
OLS Ridge PC
Predictor Estimator b
s
VIF Estimator Estimator
Intercept 15.077*** 14.995 14.994
Cohabiting couple .083 .005 1.187 .109 .132
Biological children 1.306*** .147 1.575 1.242 1.332
Stepchildren .975*** .079 1.303 .923 1.007
First union .552*** .063 1.605 .484 .510
Minority couple .022 .002 1.100 .041 .027
Male age (b
6
) .011 .036 10.184 .024 .028
Female age (b
7
) .003 .009 16.863 .021 .033
Male age at union (b
8
) .048 .093 5.245 .032 .029
Female age at union (b
9
) .059 .107 6.615 .034 .022
Union duration (b
10
) .075 .258 26.583 .040 .025
R
2
.155***
Panel B: Partial Collinearity Diagnostics
Variance Proportions
λ No. λ Value 兹φ
苶
p
j6
p
j7
p
j8
p
j9
p
j10
10 .007 31.197 .734 .121 .653 .128 .051
11 .004 41.329 .186 .836 .141 .685 .914
*** p .001.
c06.qxd 8/27/2004 2:53 PM Page 230

linear dependencies among the regressors. The variance proportions associated
with eigenvalue number 10 indicate a correlation between male age and male age
at union. Those associated with eigenvalue number 11 suggest that female age,
female age at union, and union duration are somewhat linearly dependent. These
are all precisely the variables that would be exactly collinear were it not for
missing data.
Alternatives to OLS When Regressors Are Collinear
Several simple remedies for collinearity problems were discussed in Chapter 3,
including dropping redundant variables, incorporating variables into a scale, employ-
ing nonlinear transformations, and centering (for collinearity arising from cross-prod-
uct terms). However, there are times when none of these solutions are satisfactory. For
example, in the body fat data, I may want to know the effect of, say, triceps skinfold
thickness on body fat, net of (i.e., controlling for) the effects of thigh circumference
and midarm circumference. Or, in the NSFH example, I may want to tease out the sep-
arate effects of male- and female age, male- and female age at the beginning of the
union,and union duration, on couple disagreement. None of the simple remedies are
useful in these situations. With this in mind, I will discuss two alternatives to OLS:
ridge regression and principal components regression. These techniques are some-
what controversial (see, e.g., Draper and Smith, 1998; Hadi and Ling, 1998).
Nevertheless, they may offer an improvement in the estimates of regressor effects
when collinearity is severe.
First we need to consider a key tool in the evaluation of parameter estimators: the
mean squared error of the estimator, denoted MSQE (to avoid confusion with the MSE
in regression). Let θ be any parameter and θ
ˆ
its sample estimator. Then MSQE(θ
ˆ
)
E
θ
ˆ
(θ
ˆ
θ)
2
. That is, MSQE(θ
ˆ
) is the average, over the sampling distribution of θ
ˆ
, of the
squared distance of θ
ˆ
from θ. All else equal, estimators with a small MSQE are pre-
ferred, since they are by definition closer, on average, to the true value of the parame-
ter, compared to other estimators. It can be shown that MSQE(θ
ˆ
) V(θ
ˆ
) [B(θ
ˆ
)]
2
,
where B(θ
ˆ
) is the bias of θ
ˆ
(defined in Chapter 1). Both ridge and principal components
regression employ biased estimators. However, both techniques offer a trade-off of a
small amount of bias in the estimator for a large reduction in its sampling variance.
Ideally, this means that these techniques bring about a substantial reduction in the
MSQE of the regression coefficients compared to OLS.
At the same time, both techniques have a major drawback, particularly in the
social sciences, where hypothesis testing is so important: The extent of bias in the
regression coefficients is unknown. Therefore, significance tests are not possible. To
understand why, consider the test statistic for the null hypothesis that β
k
0. For sim-
plicity, suppose that the true variance of b
k
is known and that n is large, so that t tests
and z tests are equivalent. The test relies on the fact that b
k
is unbiased for β
k
. Now
the test statistic is
z
b
k
σ
b
β
k
k,0
,
REGRESSION DIAGNOSTICS II: MULTICOLLINEARITY 231
c06.qxd 8/27/2004 2:53 PM Page 231

where β
k,0
is the null-hypothesized value of β
k
, which in this case is zero. Therefore,
if β
k
is truly zero, that is, the null hypothesis is true, then
E(z) E
冢
b
k
σ
b
β
k
k,0
冣
σ
1
b
k
[E(b
k
) β
k,0
]
σ
1
b
k
(0 0) 0 (6.15)
and
V
冢
b
k
σ
b
β
k
k,0
冣
σ
1
b
k
2
V(b
k
)
σ
σ
b
b
k
2
k
2
1. (6.16)
That is, the test statistic has the standard normal distribution under the null hypoth-
esis. Therefore, a value of 2 implies a sample coefficient that is 2 standard deviations
above its expected value under the null, and the probability of this is less than .05.
But suppose that b
k
is biased and its expected value is unknown. Then z would still
be normally distributed and (6.16) would still hold under the null hypothesis. But
(6.15) is no longer necessarily valid, since the expected value of the estimator is no
longer necessarily zero under the null. This means that the exact distribution of the
test statistic under the null hypothesis is no longer known, and the probability of get-
ting, say, a value of 2 cannot be determined. Given this limitation, these techniques
are useful only to the extent that the values of the coefficients themselves, rather than
whether they are “significant,” are of primary importance.
Ridge Regression. In ridge regression, we add a small value, called the ridge con-
stant, to the diagonals of the design matrix prior to computing R
1
xx
r
xy
. What does this
do for us? To answer this, first consider the design matrix when there is no collinear-
ity. Suppose that we have a simple model with only two regressors and the correla-
tion between them (r
12
) is .5. Suppose further that the true model for the
standardized variables is Y
z
.25Z
1
.15Z
2
ε*, where ε* is uncorrelated with the
regressors. This implies that the correlation of Y with Z
1
is .325 and with Z
2
is .275
(as the reader can verify using covariance algebra). If we have sample data that
reflect population values perfectly, the standardized coefficient estimates are
b
s
R
1
xx
r
xy
冤冥
1
冤冥
冤冥冤冥
冤冥
.
The OLS estimator gives us the true coefficients. Now suppose that we perturb r
xy
slightly to simulate sampling variability. Arbitrarily, I add .01 to the first correlation
and subtract .01 from the second. Now we have
b
s
R
1
xx
r
xy
冤冥冤冥
冤冥
.
The OLS estimator is slightly off but still pretty close to the true coefficients.
On the other hand, let’s say the correlation between the regressors is .995. Using
the same true regression parameters, the correlation of Y with Z
1
is now .39925 and
.27
.13
.335
.265
1.3333 .6667
.6667 1.3333
.25
.15
.325
.275
1.3333 .6667
.6667 1.3333
.325
.275
1.5
.5 1
232 ADVANCED ISSUES IN MULTIPLE REGRESSION
c06.qxd 8/27/2004 2:53 PM Page 232

with Z
2
is .39875. As before, with sample data that exactly reflect population values,
we have
b
s
R
1
xx
r
xy
冤冥
1
冤冥
冤冥冤冥
冤冥
.
Once again, the OLS estimator gives us the true coefficients. However, now when we
perturb r
xy
in the same fashion—adding and subtracting .01—we get
b
s
R
1
xx
r
xy
冤冥冤冥
冤冥
.
In this case, both standardized coefficients are not only way off but also outside their
conventional range of [ 1, 1]. Moreover, the coefficient for Z
2
is of the wrong sign.
The problem is that the diagonal elements of R
1
xx
no longer dominate the matrix as they
did when r
12
was .5. In the former case the ratio of the absolute value of the diagonal to
the off-diagonal element was 2. In the current case it is 1.005. So the ridge-regression
approach adds a constant, δ, where 0 δ 1, to the diagonal entries of R
xx
in order to
make the diagonal of R
1
xx
more dominant. After experimenting with different constants
(more on choosing δ below), I decided to use a value of .15. The estimator is now
b
s
rr
R
1
xx
r
xy
冤冥
1
冤冥
冤冥冤冥
冤冥
,
where “rr” stands for “ridge regression.” Notice, first, that the ratio of diagonal to
off-diagonal elements of R
1
xx
has increased to 1.156. More important, the coefficient
estimates are now fairly close to the true parameter values.
In general, ridge regression calls for replacing (X*X*) with (X*X* δI). The
estimator is then b
s
rr
(X*′X* δI)
1
r
xy
. The ridge estimator has substantially
smaller variance than the OLS estimator, since the sum of the variances of the ridge
coefficients is (Myers, 1986)
冱
V(b
s
k,rr
)
冱
K
i1
(λ
σ
i
*
2
λ
δ
i
)
2
,
which can be compared to the comparable expression for OLS shown in equation
(6.11). On the other hand, the bias of the estimator is easily seen. Because the OLS
estimator can be written
b
s
R
xx
1
1
n
Zy
z
R
xx
1
1
n
Z(Z
ββ
s
εε
*) R
xx
1
1
n
ZZ
ββ
s
R
xx
1
1
n
Z
εε
*,
its expected value is
E(b
s
) R
xx
1
1
n
ZZ
ββ
s
R
xx
1
1
n
ZE(
εε
*) R
xx
1
R
xx
ββ
s
ββ
s
,
.2521
.1199
.40925
.39975
3.4589 2.9927
2.9927 3.4589
.40925
.38875
1.15 .995
.995 1.15
2.25
1.85
.40925
.38875
100.2506 99.7494
99.7494 100.2506
.25
.15
.39925
.39875
100.2506 99.7494
99.7494 100.2506
.39925
.39875
1 .995
.995 1
REGRESSION DIAGNOSTICS II: MULTICOLLINEARITY 233
c06.qxd 8/27/2004 2:53 PM Page 233
showing that the OLS estimator is unbiased. Comparable operations for the ridge
estimator give us
E(b
s
rr
) (R
xx
δδ
I)
1
R
xx
ββ
s
ββ
s
.
Choosing
δδ
. Choosing the appropriate value of the ridge constant is more art than
science. There are a number of criteria to use [see Myers (1986) for a description of
several], but all revolve around plotting some criterion value against a succession of
values for δ and choosing the δ that produces the “best” criterion. One relatively
straightforward method is to use the ridge trace for each parameter estimate. This is
a plot of the estimate against a succession of values for δ ranging from 0 to 1. Recall
that the coefficients tend to be wildly inflated in magnitude and perhaps of the wrong
sign under collinearity. The ridge traces for the different coefficients reveal how the
coefficients shrink toward more tenable values as δ is increased until, after some
value of δ, call this δ*, there is little additional change in the coefficients. The value
of δ* is then chosen as the best ridge constant to use.
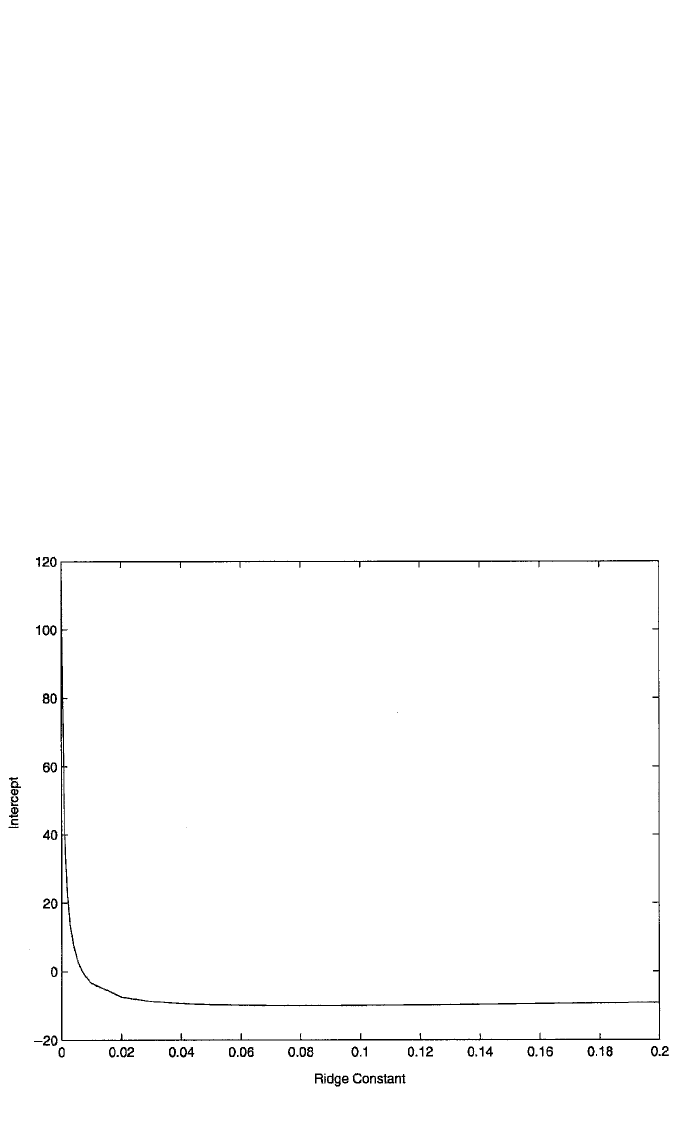
Ridge Regression with the Body Fat and NSFH Data. Figures 6.4 through 6.7
present the ridge traces for the intercept and the three regressors in the body fat data.
234 ADVANCED ISSUES IN MULTIPLE REGRESSION
Figure 6.4 Ridge trace for the equation intercept in the regression model for body fat.
c06.qxd 8/27/2004 2:53 PM Page 234
