Alfred DeMaris - Regression with Social Data, Modeling Continuous and Limited Response Variables

Подождите немного. Документ загружается.

likelihood rather than least squares. We proceed as follows. If π

is the probability

that Y

equals 1, and 1 ⫺ π

is the probability that Y

⫽ 0, we can write the discrete

density function for the Y

f(y

) ⫽ π

(1 ⫺ π

)

1⫺y

This function gives us the probability that Y takes on either value in its range f(1) ⫽

(1 ⫺ π

)

1⫺1

⫽ π

and f(0) ⫽ π

(1 ⫺ π

)

1⫺0

⫽1 ⫺ π

. Now, the probability of observ-

ing y, a particular collection of ones and zeros, is

f(y) ⫽

兿

i⫽1

(1 ⫺ π

)

1⫺y

(7.12)

Substituting (7.8) for π

in (7.12) results in the likelihood function for the probit

model:

ββ

冟y,x) ⫽

兿

i⫽1

Φ(z

)

[1 ⫺ Φ(z

)]

1⫺y

Substituting (7.9) into (7.12) gives us the likelihood for the logit model:

ββ

冟y,x) ⫽

兿

i⫽1

Λ(z

)

[1 ⫺ Λ(z

)]

1⫺y

The idea behind maximum likelihood estimation is to ﬁnd the β values that max-

imize the likelihood function, or equivalently, the log of the likelihood function. For

example, the log of the likelihood function for logistic regression is

艎(

ββ

冟y,x) ⫽

冱

i⫽1

冤

ᎏ

1⫹

(

⬘

ββ

⬘

)

ββ

)

ᎏ

⫹ (1 ⫺ y

)ln

ᎏ

1⫹ex

p(x

⬘

ββ

)

ᎏ

冥

, (7.13)

where x

⬘

ββ

represents 冱β

(see Appendix A, Section V.J). To ﬁnd the coeﬃcient

estimates for the logit model, one takes the ﬁrst partial derivatives of (7.13) with

respect to each of the β’s, sets them to zero, and then solves the set of simultaneous

equations for b. (The same idea applies to the probit model.) As this is a system of

nonlinear equations, an iterative procedure is required [see Long (1997) for details].

The matrix of second derivatives of (7.13) with respect to the parameters is called

the Hessian (the same applies to probit), and the inverse of the negative of the

expected value of the Hessian is the variance–covariance matrix for the parameter

estimates (Long, 1997). The estimate of this matrix provides the estimated standard

errors of the coeﬃcients. With large samples, as noted in Chapter 1, MLEs tend to

be unbiased, consistent, eﬃcient, and normally distributed.

Inferences in Logit and Probit

There are several inferential tests of interest in probit and logit that are analogous to

those in linear regression. First, the logit/probit counterpart to the global F test in lin-

ear regression is the likelihood-ratio chi-squared test, also called the model chi-squared.

Let L

denote the likelihood function evaluated at the MLE for an intercept-only

NONLINEAR PROBABILITY MODELS 255

c07.qxd 8/27/2004 2:54 PM Page 255

model, and L

denote the likelihood function evaluated at the MLEs for the hypoth-

esized model. Then the model χ

model χ

⫽⫺2ln

ᎏ

⫽⫺2lnL

⫺ (⫺2lnL

The log of L

can be computed by plugging the coeﬃcient estimates into the probit

or logit likelihood and then logging the result. In particular, ln L

in logistic regres-

sion would be computed by evaluating (7.13) with

ββ

substituted in place of

ββ

. For

the logistic regression of violence on the couple characteristics shown in Table 1,

⫺2 ln L

is 3054.132.

In binary response models, the likelihood evaluated under the MLE for an intercept-

only model has an especially simple form. In the absence of any covariates in the

model, the MLE for π

is just p, the sample proportion in the interest category on Y. L

is, therefore,

⫽

兿

i⫽1

(1 ⫺ p)

1⫺y

⫽ p

(1 ⫺ p)

where n

is the number of cases with Y equal to 1 and n

is the number of cases with

Y equal to 0. For the violence example, the null likelihood is

⫽ (.1355)

555

(1 ⫺ .1355)

3540

and thus the log-likelihood is

ln L

⫽ 555 ln(.1355) ⫹ 3540 ln(1 ⫺ .1355) ⫽⫺1624.763,

implying that

⫺2lnL

⫽⫺2(⫺1624.763) ⫽ 3249.526.

The model χ

for the logistic regression of violence is, therefore, 3249.526 ⫺

3054.132 ⫽ 195.394. Under the null hypothesis that the β’s for all of the explanatory

variables equal zero, the model χ

is distributed as chi-squared with K degrees of

freedom, where K, as always, indicates the number of regressors in the model. In this

case, the df is 7, and the result is very signiﬁcant, suggesting that at least one of the

regression coeﬃcients is not zero.

Tests for nested models are accomplished with a nested χ

test, analogous to the

nested F test in OLS. If model B is nested inside model A, a test for the validity of

the constraints on A that lead to B is

nested χ

⫽ model χ

for A ⫺ model χ

for B,

256 REGRESSION WITH A BINARY RESPONSE

c07.qxd 8/27/2004 2:54 PM Page 256

which under the null hypothesis that the constraints are valid is chi-squared with

degrees of freedom equal to the number of constraints imposed (e.g., the number of

parameters set to zero).

As the coeﬃcient estimates are normally distributed for large n, we use a z test to

test H

: β

⫽ 0. The test is of the form

z ⫽

ᎏ

where σ

is the estimated standard error of b

. The square of z is what is actually

reported in some software (e.g., SAS), and z

is referred to as the Wald chi-squared since

it has a chi-squared distribution with 1 degree of freedom under H

. This test is asymp-

totically equivalent to the nested χ

that would be found from comparing models with

and without the predictor in question. However, the reader should be cautioned that

Wald’s test can behave in an aberrant manner when an eﬀect is too large. In particular,

the Wald statistic shrinks toward zero as the absolute value of the parameter estimate

increases without bound (Hauck and Donner, 1977). Therefore, when in doubt, the

nested χ

is to be preferred over the Wald test for testing individual coeﬃcients.

Conﬁdence intervals for logit or probit coeﬃcients are also based on the asymp-

totic normality of the coeﬃcient estimates. Thus, a 95% conﬁdence interval for β

either type of model takes the form b

⫾ 1.96σ

. This formula applies generically to

any coeﬃcient estimates that are based on maximum likelihood estimation and is

relevant to all the models discussed from this point on in the book. I therefore omit

coverage of conﬁdence intervals in subsequent chapters.

More about the Likelihood. As the likelihood function is liable to be relatively

unfamiliar to many readers, it is worth discussing in a bit more detail. It turns out

that this function taps the indeterminacy in Y under a given model, much like the

total and residual sums of squares do, in linear regression. By indeterminacy, I

mean the uncertainty of prediction of Y under a particular model. For example, in

OLS, if the “model” for Y is a constant, µ, estimated in the sample by y

苶

, the inde-

terminacy in Y with respect to this model is TSS ⫽ the sum of squares around y

苶

. This,

of course, is the naive model, which posits that Y is unrelated to the explanatory vari-

ables. TSS measures the total amount of indeterminacy in Y that is potentially

“explainable” by the regression. On the other hand, SSE, which equals the sum of

squares around y

, is the indeterminacy in Y with respect to the hypothesized model.

If the model accounts perfectly for Y, then Y ⫽ y

for all cases, and SSE is zero.

In linear regression, we rely on the squared deviation of Y from its predicted value

under a given model to tap uncertainty. The counterpart in MLE is the likelihood of

Y under a particular model. The greater the likelihood of the data, given the param-

eters, the more conﬁdent we are that the process that generated Y has been identiﬁed

correctly. Under the naive model, the process that generated Y is captured by p, and

⫺2lnL

reﬂects the total uncertainty in Y that remains to be explained. The indeter-

minacy under the hypothesized model is ⫺2lnL

. What happens if Y is predicted

NONLINEAR PROBABILITY MODELS 257

c07.qxd 8/27/2004 2:54 PM Page 257

perfectly by the model? Let’s rewrite the likelihood function as a general expression,

with π

denoting the predicted probability that Y ⫽ 1 for the ith case. We begin with

(7.12), but substitute π

, and write it as follows. Let 1 represent the set of cases with

Y equal to 1, and 0 the set of cases with Y equal to zero. Then we have

ββ

冟y,x) ⫽

兿

y∈1

兿

y∈1

(1 ⫺ π

Now if Y is perfectly predicted, π

⫽ 1 when Y ⫽ 1 and π

⫽ 0 when Y ⫽ 0. We then

have

ββ

冟y,x) ⫽

兿

y∈1

兿

y∈1

(1 ⫺ 0) ⫽ 1,

in which case ⫺2 ln(1) ⫽ 0. In other words, the closer to zero ⫺2 ln L is, the less

uncertainty there is about Y under the model. The larger ⫺2 ln L is, the poorer the

model is in accounting for the data. The model χ

simply tells us how much the orig-

inal level of indeterminacy in Y—from using the naive model—is reduced under the

hypothesized model. We will see below that this reasoning leads to one of the R

analogs used in models employing MLE.

Logit and Probit Analyses of Violence

Logit and probit estimates for the regression of violence on couple characteristics are

shown in the “logit” and “probit” columns of Table 7.1. Model χ

values suggest that

both models are signiﬁcant. Substantively, the logit and probit results tend to agree

with the OLS ones: cohabiting instead of being married, being a minority couple,

male isolation, economic disadvantage, and having an alcohol or drug problem all

elevate the probability of violence, while longer relationship durations and older

ages at inception of the union lower it. Z ratios for tests of logit and probit

coeﬃcients, with the exception of that for the intercept, are roughly comparable to

the OLS t ratios. The eﬀect of being a minority couple is just signiﬁcant in logit and

probit, but just misses being signiﬁcant in OLS. Otherwise, all regressor eﬀects are

signiﬁcant, across all models.

However, predicted probabilities generated by logit and probit, particularly near

the extremes of 0 or 1, depart from those of OLS. For example, suppose that we rees-

timate the probability of violence for our low-risk couple described above. We saw

above that it was ⫺.069 for OLS. For the logistic regression model, we ﬁrst calcu-

late the predicted logit:

ᎏ

1⫺

ᎏ

⫽⫺2.151 ⫺ .046(2)(12.823) ⫺ .027(2)(7.081)

⫹ .020(2)(⫺6.296) ⫹ .023(⫺5.128) ⫽⫺4.083.

Then the predicted probability is

⫽

ᎏ

1 ⫹

(

⫺

(⫺

)

ᎏ

⫽ .017.

258 REGRESSION WITH A BINARY RESPONSE

c07.qxd 8/27/2004 2:54 PM Page 258

In probit, we estimate

⫺1

(π

) ⫽⫺1.247 ⫺ .023(2)(12.823) ⫺ .014(2)(7.081)

⫹ .011(2)(⫺6.296) ⫹ .012(⫺5.128) ⫽⫺2.235.

Then the estimated probability is Φ(⫺2.235) ⫽ .013.

Interpreting the Coefficients. One way to interpret logit and probit coeﬃcients is in

terms of their eﬀects on Y* in the regression model for the latent scale, as the

logit/probit coeﬃcients are estimates of the β

in this regression. However, presum-

ing that Y is a binary proxy for an underlying continuous variable may not always

make sense. Instead, the β

can be interpreted in terms of the probability of being in

the interest category on Y—but there’s a catch. In OLS, the partial derivative of E(Y )

with respect to X

is a constant value, β

, regardless of the levels of the regressors.

This is no longer true in nonlinear models, as we saw in Chapter 5. Recalling that

both the logit and the probit model for π

are distribution functions, we can derive a

general expression for the partial derivative of a distribution function of x

⬘β, with

respect to X

. Employing the chain rule (Appendix A, Section IV.B) yields

ᎏ

∂

ᎏ

F(x

⬘

ββ

) ⫽

ᎏ

∂x

∂

⬘

ββ

ᎏ

F(x

⬘

ββ

)

ᎏ

∂

ᎏ(

⬘

ββ

)

⫽ f(x

⬘

ββ

)β

. (7.14)

Applying (7.14) to the logit and probit models, the partial derivatives are as follows.

For logit:

ᎏ

∂

ᎏπ

⫽

ᎏ

∂

ᎏΛ

⬘

ββ

)

⫽ λ

⬘

ββ

)β

⫽

ᎏ

1⫹

(

⬘

ββ

⬘

)

ββ

)

ᎏ

1⫹ ex

p(x

⬘

ββ

)

ᎏ

⫽ π

(1 ⫺ π

)β

. (7.15)

For the probit model we have

ᎏ

∂

ᎏπ

⫽

ᎏ

∂

ᎏΦ

⬘

ββ

)

⫽

φ(x

⬘

ββ

)β

⫽

冦

ᎏ

兹

苶

ᎏ

exp

冤

⫺

ᎏ

冢

⬘

ββ

冣

冥冧

. (7.16)

Expressions (7.15) and (7.16) make it clear that the partial slope of X

with respect

to π

in logit and probit is not a constant but is rather dependent on a particular value

NONLINEAR PROBABILITY MODELS 259

c07.qxd 8/27/2004 2:54 PM Page 259

of the linear predictor, x

⬘β, which, in turn, varies with the regressors. For example,

in logistic regression the estimated partial slope for the probability of violence with

respect to relationship duration, for our low-risk couple, is

ᎏ

∂

ᎏπ

⫽ (.017)(1 ⫺ .017)(⫺.046) ⫽⫺.00077.

For the probit model we have

ᎏ

∂

ᎏπ

⫽

冦

ᎏ

兹

苶

ᎏ

exp

冤

⫺

ᎏ

(⫺2.235)

冥冧

(⫺.023) ⫽⫺.00075,

which, despite diﬀerences in b

, is essentially the same as for logit. In that the cor-

rection factors in the partial slope, φ(x

⬘

ββ

) for probit and λ( x

⬘

ββ

) for logit, are always

positive and less than 1, the b

can be interpreted as the eﬀects on the probability

apart from an attenuation factor. Hence positive coeﬃcients indicate regressors with

positive eﬀects on the probability, and negative regressors indicate regressors with

negative eﬀects. Beyond this, the coeﬃcients do not have an intuitively simple inter-

pretation. (We will see below, however, that the logit coeﬃcients, when exponenti-

ated, have a particularly appealing interpretation.)

Alternative Models. An artifact of both logit and probit models is that the eﬀect of

a regressor on the probability, as indicated by the partial derivative, is always

at its maximum when π equals .5. In this case, the attenuation factor for logit

reaches its maximum value of (.5)(1 ⫺ .5) ⫽ .25. In the probit model, when the lin-

ear predictor is zero, π ⫽ Φ(0) ⫽ .5, and the attenuation factor reaches its maximum

value of 1/兹2

苶

⫽ .399. Nagler (1994) pointed out that this is a limitation of logit

and probit models. People with an initial probability of an event of .5 will be indi-

cated to be most susceptible to regressor eﬀects (i.e., the partial eﬀect of each X

will reach its maximum value) due to a phenomenon that is imposed by the model

speciﬁcation. He therefore proposed using an alternative model when sensitivity of

people’s probabilities of events to regressor eﬀects was important in one’s investi-

gation. The model, called scobit for “skewed logit” (Nagler, 1994, p. 235), allows

the probability at which people are most susceptible to regressors to be estimated

from the data.

The scobit model is based on the Burr-10 distribution, which unlike logit and pro-

bit, is an asymmetric distribution. The formula for this distribution function is

(x) ⫽

冤

ᎏ

1 ⫹

(

(x)

ᎏ

冥

When α ⫽ 1, this reduces to the logit distribution. Hence, the logit model is nested

inside the scobit model, and a nested chi-squared test can be used to determine

whether scobit is an improvement over logit. The scobit model is developed with the

same latent-scale formulation as logit and probit except that the Burr-10 distribution

replaces the standard normal or standard logistic distribution. Once again, we assume

a latent scale, Y*, such that Y

⫽

冱β

⫹ ε

. This time, we assume that ε

follows the

260 REGRESSION WITH A BINARY RESPONSE

c07.qxd 8/27/2004 2:54 PM Page 260

Burr-10 distribution. Then

P(Y

⫽ 1) ⫽ P(Y

⬎ 0) ⫽ P

冢

冱

⫹ ε

⬎ 0

冣

⫽ P

冢

⬎⫺

冱

冣

However, because the Burr-10 distribution is not symmetric, this does not equal expres-

sion (7.4). Instead, because of the principle that P(x ⬎ c) ⫽ 1 ⫺ P(x ⬍ c), we have that

P(Y

⫽ 1) ⫽ 1 ⫺ P

冢

⬍⫺

冱

冣

⫽ 1 ⫺

冤

ᎏ

1⫹

(

⫺

(⫺

冱

)

ᎏ

冥

, (7.17)

which we denote as G(x

⬘

ββ

). Again, it is easy to show that if α⫽ 1, G(x

⬘

ββ

) ⫽

Λ(x

⬘

ββ

). Unlike the case with logit and probit models, there is no link function that

linearizes (7.17) when α is not equal to 1.The probability, π*, at which people are

most susceptible to eﬀects of explanatory variables is given by

π* ⫽ 1 ⫺

冢

ᎏ

1 ⫹

ᎏ

冣

(Nagler, 1994). As is evident, if α ⫽ 1, π* ⫽ .5, the π* for the logit model. Also, π*

converges to zero as α converges to zero; as α tends to inﬁnity, however, π* reaches

a maximum value of about .632 (Nagler, 1994).

Another asymmetric distribution that can be employed as a probability model is

the complementary log-log model (Agresti, 2002; Long, 1997):

⫽ H(x

⬘

ββ

) ⫽ 1 ⫺ exp[⫺ exp(x

⬘

ββ

)]. (7.18)

The link function that linearizes (7.18) is

ln[⫺ln(1 ⫺ π

)] ⫽

冱

The likelihood function for this model becomes important in Chapter 10; therefore,

I give it here:

ββ

冟y,x) ⫽

兿

i⫽1

(1 ⫺ π

)

1⫺y

⫽

兿

i⫽1

[1 ⫺ exp(⫺exp(x

⬘

ββ

))]

[exp(⫺exp(x

⬘

ββ

))]

1⫺y

⫽

兿

y∈0

[exp(⫺exp(x

⬘

ββ

))]

兿

y ∈1

[1 ⫺ exp(⫺exp(x

⬘

ββ

))].

Figure 7.3 shows the density functions, and Figure 7.4 shows the distribution

functions for the scobit and complementary log-log models. The asymmetery of the

NONLINEAR PROBABILITY MODELS 261

c07.qxd 8/27/2004 2:54 PM Page 261

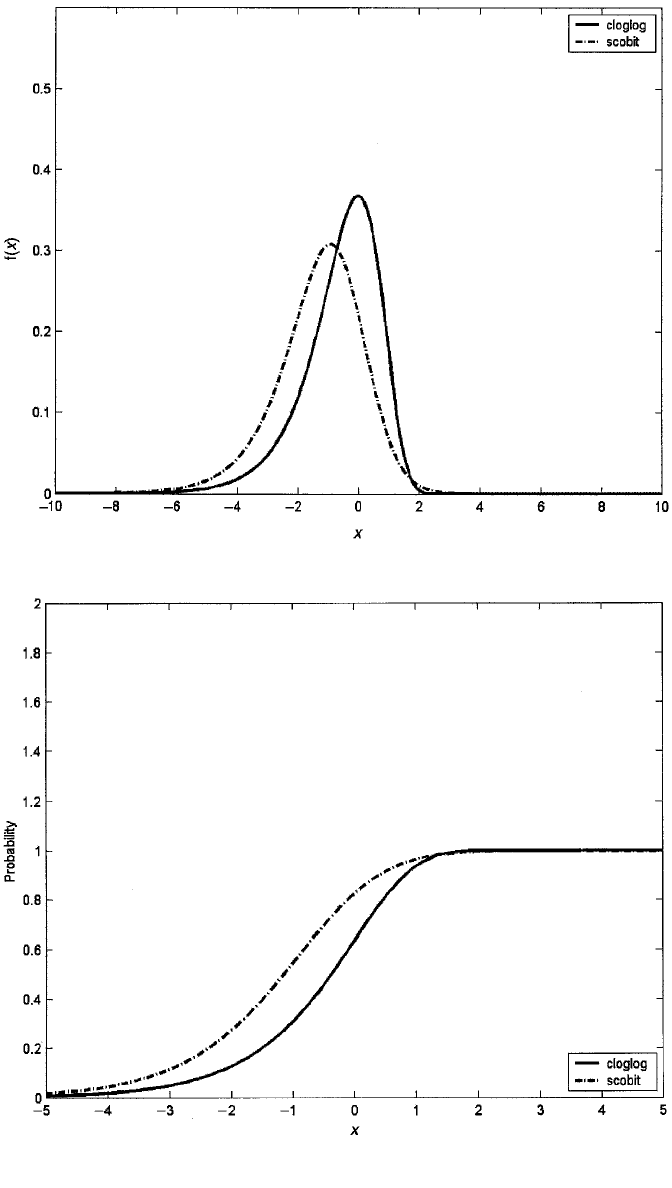
Figure 7.3 Scobit and complementary log-log densities.

Figure 7.4 Scobit and complementary log-log distributions.

c07.qxd 8/27/2004 2:54 PM Page 262

densities is evident in Figure 7.3, which reveals both densities to be skewed to the

left. In contrast to the logit and probit distributions, the functions in Figure 7.4 both

approach 1 more rapidly than they approach 0; this is particularly true for the com-

plementary log-log model. In fact, Agresti (2002) remarks that logit and probit mod-

els are not appropriate when π increases from 0 fairly slowly but approaches 1 quite

suddenly (see his monograph for an application in which this is the case). In that sit-

uation, the complementary log-log model would be most appropriate. Table 7.2 pres-

ents the scobit and complementary log-log estimates for the regression of violence.

Although the intercepts diverge, the regressor coeﬃcients from each model are very

similar in value. Apart from an attenuation factor, the coeﬃcients indicate eﬀects on

π and are in substantive agreement with the logit and probit eﬀects. The nested test

for scobit versus logit is shown as the “χ

for alpha” in the table and is a test for H

α ⫽ 1. Because the test is nonsigniﬁcant, scobit appears to oﬀer no improvement

over the logit model. (The scobit model is available in STATA, whereas the comple-

mentary log-log model is available in SAS.)

Interpreting the Partial Derivative, Revisited. It is tempting to interpret the par-

tial derivative in nonlinear probability models as the change in the probability for

a unit increase in a given predictor, net of other regressors (e.g., Cleary and Angel,

1984). This is, of course, the unit-impact interpretation appropriate in the LPM.

Although the partial derivative is, at times, a very close approximation to such a

change, this interpretation is not technically correct, as has been observed else-

where (DeMaris, 1993, 2003; Petersen, 1985). The reason is illustrated in Figure

7.5, which shows how closely the partial derivative approximates the change in

P( x) ⫽ exp( x)/ [1 ⫹ exp( x)] from x ⫽ 1 to x ⫽ 2, a unit change. Notice that this is

just a logistic regression model with β

⫽ 0 and β

⫽ 1. The partial derivative at

x ⫽ 1 is P⬘(1) ⫽ P(1)[1 ⫺ P(1)]β

⫽ (.731)(1 ⫺ .731)(1) ⫽ .1966. This is the slope

of the line tangent to P( x) at x ⫽ 1, as shown in the ﬁgure. Now the slope of that

line indicates change along the line for each unit increase in x, but

not change along the function, as it is clear that the line does not follow the func-

tion very closely. Change along the function for a unit increase in x at x ⫽ 1 is

given by

P(2) ⫺ P(1) ⫽

ᎏ

1 ⫹

ᎏ

⫺

ᎏ

1 ⫹

ᎏ

⫽ .8808 ⫺ .73106 ⫽ .1497.

As .1966 is not very close to .1497, P⬘(1) is not a good approximation to the unit

impact. On the other hand, if a unit change represents a very small change in a pre-

dictor, the partial derivative will be a close approximation to the unit impact. But in

general, the accurate way to assess the change in probability for a unit increase in

, net of other predictors, is to evaluate F( x

⫹ 1 冟 x

⫺k

) ⫺ F( x

冟x

⫺k

), where F rep-

resents the probability model of interest (e.g., logit, probit, scobit, complementary

log-log).

NONLINEAR PROBABILITY MODELS 263

c07.qxd 8/27/2004 2:54 PM Page 263

Interpeting Logit Models: Odds and Odds Ratios. Logit models have an advantage

over other models in interpretability, because exp(β

) can be interpreted as the mul-

tiplicative impact on the odds of an event for a unit increase in X

, net of the other

covariates. Indeed, exp(β

) is the multiplicative analog of β

in the linear regression

model. To understand why this is so, we exponentiate both sides of equation (7.11)

to express the logit model as

exp

冢

ᎏ

1 ⫺

ᎏ

冣

⫽ exp

冢

冱

冣

264 REGRESSION WITH A BINARY RESPONSE

Table 7.2 Scobit and Complementary Log-Log Estimates for the Regression

of Violence on Couple Characteristics

Model

Predictor Estimate Scobit Cloglog

Intercept b ⫺14.922 ⫺2.207***

728.360 .061

t or z ⫺.020 ⫺36.064

Relationship duration b ⫺.044*** ⫺.044***

.005 .005

t or z ⫺9.311 ⫺9.330

Cohabiting b .685*** .685***

.195 .194

t or z 3.519 3.530

Minority couple b .192* .192*

.098 .098

t or z 1.959 1.959

Female’s age at union b ⫺.025*** ⫺.025***

.007 .007

t or z ⫺3.634 ⫺3.624

Male’s isolation b .018* .018*

.007 .007

t or z 2.528 2.515

Economic disadvantage b .022** .022**

.008 .008

t or z 2.705 2.710

Alcohol/drug problem b .902*** .902***

.130 .130

t or z 6.944 6.945

α 332675.100

Model χ

(7 df ) 196.686*** 196.685***

(1 df ) for α 1.290

.061 .061

.047

GSC

.086

* p ⬍ .05. ** p ⬍ .01. *** p ⬍ .001.

c07.qxd 8/27/2004 2:54 PM Page 264