Alfred DeMaris - Regression with Social Data, Modeling Continuous and Limited Response Variables
Подождите немного. Документ загружается.

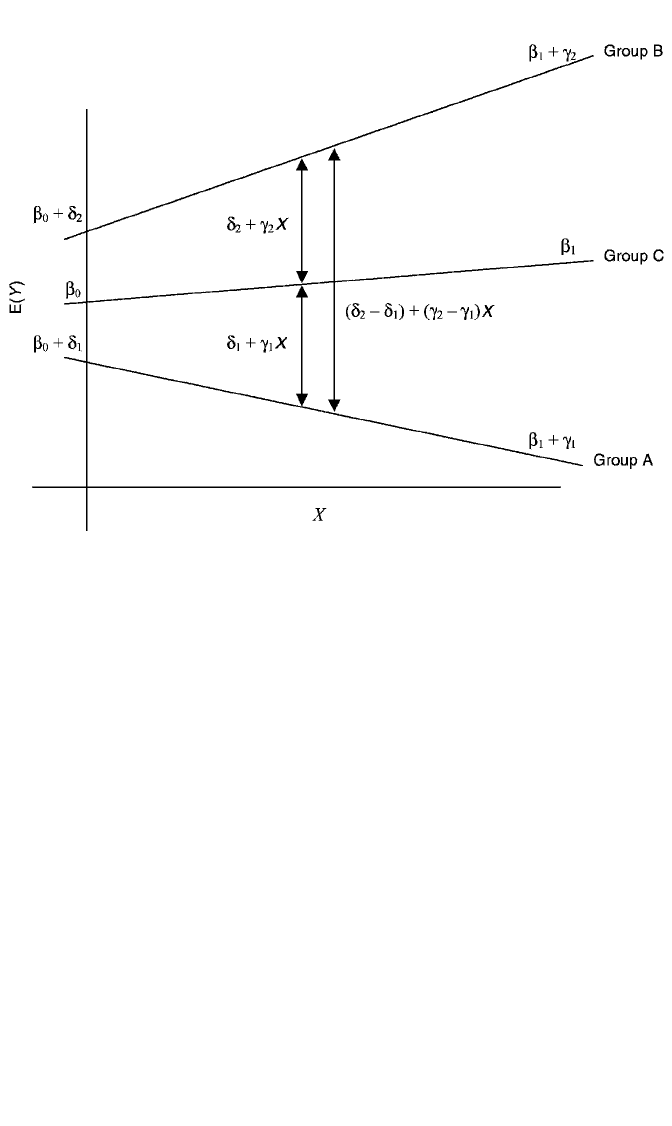
Figures 4.3 and 4.4 depict various types of disordinal interaction. Figure 4.3
shows interaction that is disordinal in X but ordinal in Z. That is, the effect of X
changes direction across groups: positive in groups B and C but negative in group A.
Nevertheless, with respect to Z, the ordering of group means is always the same, with
the mean for group B being the highest and the mean for group A being the lowest,
regardless of the level of X. Hence the effect of Z is of the same nature, regardless of
X, but varies in magnitude over the values of X. Figure 4.4 illustrates interaction that
is disordinal in both X and Z. The effect of X changes direction across groups since,
again, it’s positive in groups B and C but negative in group A. The “direction” of Z’s
effect also changes over X. This is shown by the fact that although the means for
groups A and B are always higher than the mean for group C, group A’s mean is
higher than group B’s mean at lower values of X, but lower than B’s mean at higher
values of X. In other words, the nature of Z’s effect changes over levels of X. The
only way to tell whether the interaction is ordinal or disordinal in either variable
involved in the interaction is to substitute into the equation some sample estimates
of the main-effect and interaction coefficients. After evaluating the equation for the
different groups, or at different sample values of X, it should be relatively easy to dis-
cern the nature of the interaction effect.
Interaction Models for Faculty Salary. Table 4.8 shows the results of estimating a
model for faculty salary that includes the interaction of college with marketability in
MODELS WITH BOTH CATEGORICAL AND CONTINUOUS PREDICTORS 145
Figure 4.3 Regression model E(Y) β
0
δ
1
A δ
2
B β
1
X γ
1
AX γ
2
BX, depicting interaction that is
disordinal in the effect of the continuous variable, X, but ordinal in the effect of the categorical variable, Z.
c04.qxd 8/27/2004 2:49 PM Page 145
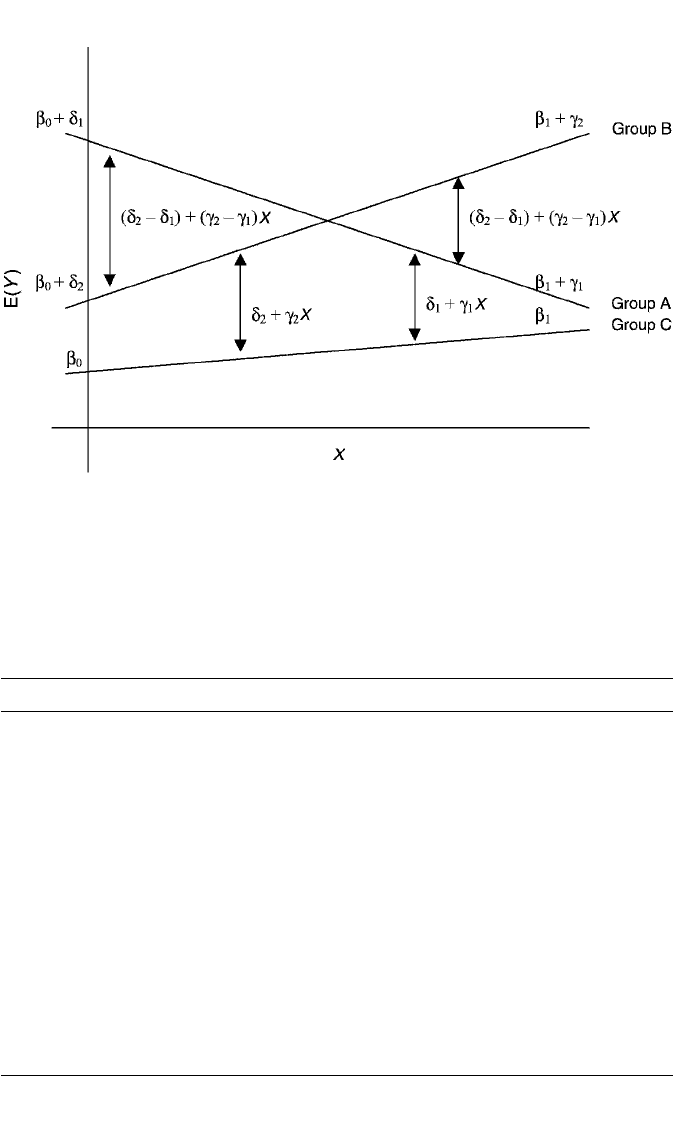
146 MULTIPLE REGRESSION WITH CATEGORICAL PREDICTORS
Figure 4.4 Regression model E(Y) β
0
δ
1
A δ
2
B β
1
X γ
1
AX γ
2
BX, depicting interaction
that is disordinal both in the effect of the continuous variable, X, and in the effect of the categorical
variable, Z.
Table 4.8 Main Effect and Interaction Models for the Regression of Academic Year
Salary on College Plus Covariates for Number of Years in Rank, Number of Years
at BG, Prior Experience, and Marketability for 725 Faculty Members
Predictor Model 1 Model 2
Intercept 47950.000*** 47958.000***
Firelands 6098.382*** 5639.779***
Business 4444.926*** 2201.368
Education 1507.845 767.187
Other 1620.079 2000.977
Years in rank
a
137.728 132.748
Years at BG
a
1093.968*** 1088.270***
Prior experience
a
952.136*** 956.563***
Marketability
a
27020.000*** 27820.000***
Marketability
a
Firelands 32394.000***
Marketability
a
Business 9392.054
Marketability
a
Education 9321.962
Marketability
a
Other 4197.697
F 144.298*** 98.524***
∆F 3.267*
R
2
.617 .624
a
Centered variable.
* p .05. ** p .01. *** p .001.
c04.qxd 8/27/2004 2:49 PM Page 146

MODELS WITH BOTH CATEGORICAL AND CONTINUOUS PREDICTORS 147
their effects on salary. For comparison purposes, the main effects (ANCOVA) model
without interaction, shown as model 2 in Table 4.5, is first reproduced here as model 1.
Model 2 adds the cross-products of marketability with the four college dummies. First
we must investigate whether the interaction is significant. As it involves four additional
terms, we perform the nested F test to compare models 1 and 2. The nested F is 3.267,
which is just significant ( p .05). Evidently, the only significant individual coefficient
is for the cross-product of marketability with the “firelands” group. Nevertheless, for
didactic purposes, I consider all of the coefficients when interpreting the interaction
effect. First, if marketability is the focus, its partial slope is
27820 32394 FIREL 9392.054 BUSINESS
9321.962 EDUCATION 4197.697 OTHER.
Here it is evident that the interaction is disordinal in marketability. Although mar-
ketability has a positive effect on salary for “arts and sciences,” “business,” “educa-
tion,” and “other departments,” its effect is estimated to be negative for “firelands.”
With a value of 27820 32394 4574, the effect suggests that a unit increase in
marketability in the Firelands college actually lowers one’s salary by $4574, on aver-
age. This seemingly counterintuitive result may make more sense when viewed from
the perspective of marketability as the moderator variable, as we do next.
With college as the focus, the dummy coefficients turn out to be:
Firelands: 5639.779 32394 marketability.
Business: 2201.368 9392.054 marketability.
Education: 767.187 9321.962 marketability.
Other: 2000.977 4197.697 marketability.
Each coefficient reflects the difference in mean salary between the indicated college
and “arts and sciences.” As is evident, this difference depends on the marketability
value for that faculty member’s discipline. The range of marketability values is .58
to 1.33, with a mean of .94 and a standard deviation of .149. Here it is important to
remember that marketability is centered. So the main effect of any given dummy
represents the difference in mean salary between the indicated college and “arts and
sciences,” at average marketability of faculty disciplines. Consider the mean salary
difference between “firelands” and “arts and sciences,” for example. At average mar-
ketability, it is 5639.779. That is, for faculty members with average marketability,
Firelands faculty make about $5640 less than Arts and Sciences faculty. However,
at 2 standard deviations below average marketability, or a value of .298, the effect
of “firelands” is 5639.779 32394(.298) 4013.633. That is, for those in less
marketable disciplines, it is more advantageous, salarywise, to be in the Firelands
college, compared to being in the College of Arts and Sciences. At 2 standard
deviations above average marketability, or a value of .298, the effect is 5639.779
32394(.298) 15293.191. The effect is clearly disordinal in college here, since
c04.qxd 8/27/2004 2:49 PM Page 147

148 MULTIPLE REGRESSION WITH CATEGORICAL PREDICTORS
Firelands faculty make a higher average salary than Arts and Sciences faculty at lower
marketability but a lower average salary at higher marketability. Similar changes in
direction of effects can be seen for the Education and Business colleges. For “educa-
tion,” the contrast with “arts and sciences” at 2 standard deviations of marketability
is 3545.132. At 2 standard deviations of marketability it is 2010.758. For “busi-
ness,” the numbers are 597.464 and 5000.200, respectively. For “other departments,”
however, average salary is always lower than for “arts and sciences,” regardless of mar-
ketability levels observed in the sample. At any rate, sample estimates suggest that
overall, the interaction is disordinal in both college and marketability.
Comparing Models across Groups, Revisited
The interaction of all model regressors with a dummy variable (or variables) repre-
senting group membership suggests that the dynamics of a given model are different
for each group. In Chapter 3 we saw that we could use a Chow test to test whether
the impact of a set of regressors on a response was different in different groups. We
can also accomplish the same task using cross-product terms. In this last section of
the chapter I show the equivalence of these two ways of addressing the same issue.
Another Look at the Chow Test. Recall that the Chow test is an omnibus test for
whether a model differs across groups: meaning whether the effect of at least one
explanatory variable is different across groups. It turns out that an assumption for
this test, as well as the equivalent test using cross-product terms, is that the error
variance in each group is the same. That is, if A and B represent the two groups in
question, and σ
2
, as usual, represents V(ε), the assumption is that σ
A
2
σ
B
2
. In
Chapter 3 I simply assumed equal error variances in the equations for academic year
salary for male and female faculty and proceeded to test whether the factors
affecting salary had the same effects for each gender. However, to ensure that the test
is valid, we must first test whether, in fact, the assumption of equal error variances
is reasonable. The following test assumes that the error variance is normally distrib-
uted in each group. The test statistic is
F
M
M
S
S
E
E
A
B
,
assuming that group A has the larger of the two error variances. If the error variance
in group B is larger, the test statistic is
F
M
M
S
S
E
E
B
A
.
Under the null hypothesis that the error variances are the same, this statistic follows the
F distribution with numerator degrees of freedom equal to the error degrees of freedom
(df
E
) for the model whose MSE is in the numerator of the test, and denominator degrees
of freedom equal to df
E
for the model whose MSE is in the denominator (Hardy, 1993).
As an example, let’s test whether the error variances for the salary models in Table 3.5
are the same for male versus female faculty. For the male faculty, the MSE is
c04.qxd 8/27/2004 2:49 PM Page 148

81171524.123, and the df
E
is 505. For the female faculty, the MSE is 52550530.18, and
the df
E
is 208. The test statistic, therefore, is
F
8
5
1
2
1
5
7
5
1
0
5
5
2
3
4
0
.
.
1
1
2
8
3
1.545.
With 505 and 208 degrees of freedom, this result is quite significant (p .001). This
suggests that the Chow test for this problem, which found the salary model to differ
for males and females, was not valid. In Chapter 6, in which weighted least squares
is introduced, we will see how to conduct a test for equality of models across two
groups under the condition of unequal error variance.
In that graduate faculty status appears to play a key role in determining faculty
salary, one question worth investigating is whether model 1 in Table 4.8 differs by
graduate faculty status. That is, do the effects of college, years in rank, years at BG,
prior experience, and marketability have different effects on salary for those who are
on the graduate faculty, as opposed to those who are not? Table 4.9 presents several
models pertinent to this question. Model 1 shows the estimated effects of these fac-
tors on salary for the 202 faculty members not on graduate faculty, while model 2
shows the results for the 523 faculty members on graduate faculty. It seems that all
of the regression coefficients are quite different in each model, with some differences
more pronounced than others. Particularly noticeable are the effects of being in the
business college, prior experience, and marketability, all of which have substantially
greater positive effects on salary for those on graduate faculty. Moreover, the effects
of being in the business college and prior experience are significant only for those
on graduate faculty. We should keep in mind, however, that any time we run sepa-
rate analyses of the same model in different subgroups, the coefficient estimates will
differ to some extent purely because of sampling error. And even though a given
effect is significant in one group but not the other, this is not enough evidence to con-
clude that the effects are significantly different in each group.
Before we can test for model differences, we must again test for the equality of
error variances in each group. The estimated error variance, or MSE, for those on
graduate faculty status is 53934137.987, with 514 df. The MSE for those not on grad-
uate faculty is 50674043.62, with 193 df. Therefore, the test statistic is
F
5
5
3
0
9
6
3
7
4
4
1
0
3
4
7
3
.9
.6
8
2
7
1.064.
With 514 and 193 df, this is not a significant result (p .3). The assumption of equal
error variance in this instance appears reasonable.
In Chapter 3 the Chow test was performed by constraining all model coefficients,
including the intercept, to be the same in each group under the null hypothesis. This
may not always be desirable. In this particular example, the intercept represents the
salary of faculty members in “arts and sciences” who are average in years in rank,
years at BG, prior experience, and marketability. It may well be that average salary
for these faculty members differs according to graduate faculty status. That is, being
on graduate faculty may add some increment to salary. But the impact on salary of
MODELS WITH BOTH CATEGORICAL AND CONTINUOUS PREDICTORS 149
c04.qxd 8/27/2004 2:49 PM Page 149

150 MULTIPLE REGRESSION WITH CATEGORICAL PREDICTORS
college, years in rank, years at BG, prior experience, or marketability may be the
same, regardless of whether or not one is on the graduate faculty. That is, in this
instance, we may want the null hypothesis to allow the intercept to differ by gradu-
ate faculty status while constraining the effects of the other regressors. We perform
the test both ways, so that the reader can see the difference in the outcomes.
The test that constrains the intercept as well as the other regressors is performed
by comparing model 1 in Table 4.8, the combined-sample model, with models 1 and
2 in Table 4.9. The test statistic is
F 35.101.
[54259263744 (9780090418.7 27722146925)]/9
(9780090418.7 27722146925)/707
Table 4.9 Regression Models Pertaining to the Interaction of Predictors of Academic
Year Salary with Whether on Graduate Faculty
Predictor Model 1 Model 2 Model 3 Model 4
Intercept 40698.000*** 50023.000*** 39891.000*** 40698.000***
Graduate faculty 10318.000*** 9324.678***
Firelands 1409.370 803.314 1960.409 1409.370
Business 714.042 6957.555*** 5547.657*** 714.042
Education 188.553 1486.229 1000.544 188.553
Other 1757.682 1543.441 1575.448 1757.682
Years in rank
a
279.113 246.232** 195.092* 279.113
Years at BG
a
1183.076*** 863.967*** 877.906*** 1183.076***
Prior experience
a
227.027 1010.841*** 845.124*** 227.027
Marketability
a
9660.048* 27146.000*** 22442.000*** 9660.048*
Graduate faculty 606.056
Firelands
Graduate faculty 6243.512**
Business
Graduate faculty 1297.677
Education
Graduate faculty 214.241
Other
Graduate faculty 525.345*
years in rank
a
Graduate faculty 319.109*
years at BG
a
Graduate faculty 783.814***
prior experience
a
Graduate faculty 17486.000***
marketability
a
SSE 9780090418.7 27722146925 41978431466 37502237344
F 55.884*** 145.241*** 188.799*** 115.595***
R
2
.699 .693 .704 .735
a
Centered variable.
* p .05. ** p .01. *** p .001.
c04.qxd 8/27/2004 2:49 PM Page 150

MODELS WITH BOTH CATEGORICAL AND CONTINUOUS PREDICTORS 151
With 9 and 707 df, this result is very significant (p .00001), resulting in rejection
of the null hypothesis. This suggests that the salary models do differ according to
graduate faculty status. However, to what extent is this result an artifact of con-
straining the intercepts to be equal? Model 3 in Table 4.9 is the same salary model
as models 1 and 2, except that it is performed on the combined sample and adds a
dummy representing graduate faculty status. Notice that the effect of graduate fac-
ulty status is quite pronounced: All else equal, being on the graduate faculty adds,
on average, $10,318 to academic year salary. Model 3 is an ANCOVA model that
allows for different intercepts according to graduate faculty status. For example, for
those not on graduate faculty, the mean salary is
E(Y ) 39891 1960.409 firelands 5547.657 business 1000.544 education
1575.448 other departments 195.092 years in rank
877.906 years at BG 845.124 prior experience 22442 marketability.
For those on graduate faculty, the mean salary is
E(Y) (39891 10318) 1960.409 firelands 5547.657 business
1000.544 education 1575.448 other departments 195.092 years in rank
877.906 years at BG 845.124 prior experience 22442 marketability.
Here, it is evident that the intercept for those not on graduate faculty is 39891, while
for those on graduate faculty it is 39891 10318 50209. The Chow test allowing
the intercepts to differ is performed by comparing model 3 to models 1 and 2.
Notice, however, that there is a change in the numerator degrees of freedom, repre-
senting the difference in the number of parameters estimated. With the intercept con-
strained, this difference is just the number of parameters in the model, since the
model is simply being duplicated in each group. With the intercept unconstrained,
there is one more parameter being estimated in the combined model than before.
Now the difference is 18 parameters in models 1 and 2 minus 10 parameters in
model 3 8 numerator degrees of freedom. The test statistic is
F 10.55.
With 8 and 707 degrees of freedom, the result is very significant (p .00001), but
the test statistic is substantially smaller compared to the result of the constrained-
intercept test. Nevertheless, we would conclude that the impact of at least one model
regressor is different for those who are on, versus not on, the graduate faculty.
Model Comparison Using Cross-Product Terms. One limitation of the Chow test
is that although it allows us to conclude that models are different across groups, it
doesn’t tell us which regressors have different effects. Performing model comparison
tests using cross-product terms rectifies that limitation. Model 4 in
Table 4.9 is model 3 with the addition of the cross-products of graduate faculty sta-
tus with all other model regressors. To compare models across levels of graduate
[41978431466 (9780090418.7 27722146925)]/8
(9780090418.7 27222146925)/707
c04.qxd 8/27/2004 2:49 PM Page 151

152 MULTIPLE REGRESSION WITH CATEGORICAL PREDICTORS
faculty status with the intercept constrained, we can perform a nested F test compar-
ing model 1 in Table 4.8 (RSS 87480506481), the ANCOVA model for faculty
salary without the dummy for graduate faculty status, with model 4 in Table 4.9
(RSS 104237532881, MSE 53044182.948), the interaction model that includes
this dummy along with the cross-product terms. The test statistic is
F 35.101,
which agrees with the result of the first Chow test above. To compare models with-
out constraining the intercept, the more usual practice, we perform a nested F test
comparing models 3 and 4 in Table 4.9. This is essentially a test for the significance
of the block of cross-product terms capturing the interaction of graduate faculty sta-
tus with all other regressors in model 3. The R
2
for model 3 is .7038 and the R
2
for
model 4 is .7354. Hence, the test statistic is
F
(.
(
7
1
3
54
.7
35
.7
4
0
)/
3
7
8
0
)
7
/8
10.55,
which also agrees with the second Chow test above. In either case, we would prefer
the interaction model over the model that does not allow interaction between gradu-
ate faculty status and the other regressors.
Model 4 also indicates which regressor effects differ by graduate faculty status via
the t tests for the cross-product terms. Apparently, the factors whose effects differ
according to graduate faculty status are being in the Business College as opposed to
being in Arts and Sciences, years in rank, years at BG, prior experience, and mar-
ketability. Interpretation of the model is facilitated by examining the partial effect of
each of these variables as a function of graduate faculty status. The impact of being
in the Business College compared to being in Arts and Sciences is 714.042
6243.512 graduate faculty. This suggests that being on the graduate faculty adds
about $6243 to the average salary gap between the Business College and the Arts and
Sciences faculty. The effect of years in rank is 279.113 525.345 graduate fac-
ulty. Thus, a greater number of years in rank reduces salary for those not on the grad-
uate faculty but enhances salary for graduate faculty members. The effect of years at
BG is 1183.076 319.109 graduate faculty. Working at BG a year longer raises
average salary more for those who are not on the graduate faculty than for those who
are. The effect of prior experience is 227.027 783.814 graduate faculty, while the
effect of marketability is 9660.048 17386 graduate faculty. Both of these regres-
sors have stronger positive effects on salary for those who are on the graduate fac-
ulty than for those who are not.
Generalizing the Chow Test. Although the Chow test examples I have used involve
only two groups, the test can be generalized to any number of groups. For example,
suppose that we wish to compare a model across three groups, denoted A, B, and C.
First, we run the model on the combined sample, either constraining the intercepts
for the groups to be equal by excluding group membership from the model (giving
(104237532881 87480506481)/9
53044182.948
c04.qxd 8/27/2004 2:49 PM Page 152

MODELS WITH BOTH CATEGORICAL AND CONTINUOUS PREDICTORS 153
us SSE
c
) or by allowing the intercepts to be unconstrained by including two dum-
mies in the model representing group membership (giving us SSE
u
). Next, we run the
model in each group separately (which gives us SSE
A
, SSE
B
, and SSE
C
). If there are
J parameters in the model (including the intercept), the test statistic with intercept
constrained is
F ,
which under the null hypothesis of no model difference across groups has the F dis-
tribution with 2J and n 3J degrees of freedom. The test statistic with the intercept
unconstrained is
F .
The combined-sample model in this case has J 2 parameters. Under the null
hypothesis of no difference across groups in the effects of the J 1 regressors in the
model, this statistic has the F distribution with 2J 2 and n 3J degrees of freedom.
Extension to more than three groups follows in a similar fashion. Examples are given
in the exercises.
Generalizing the Variance Homogeneity Test. The Chow test for model equivalence
across multiple groups assumes, as before, that the error variance is the same in each
group. Once again, this assumption can be tested. This time, however, an appropri-
ate test is Barlett’s test (Neter et al., 1985). This test is based on the assumption that
the error variance is normally distributed in each group. Let σ
ˆ
1
2
,σ
ˆ
2
2
,...,σ
ˆ
G
2
be the
estimated error variances (i.e., MSE’s) for G different groups, with error degrees of
freedom equal to df
g
, for g 1,2,...,G. Then the weighted average of the error
variances is
MSE*
d
1
f
T
冱
G
g1
df
g
σ
ˆ
2
g
,
where df
T
is the sum of the G error degrees of freedom. That is,
df
T
冱
G
g1
df
g
.
Barlett’s test statistic is then
B
C
1
冢
df
T
log MSE*
冱
G
g1
df
g
log σ
ˆ
2
g
冣
,
where “log” refers to the natural logarithm, and
C 1
3(G
1
1)
冤冢
冱
G
g1
d
1
f
g
冣
d
1
f
T
冥
For large sample sizes in each group, and under the null hypothesis that the G error
variances are equal, this test statistic has approximately a chi-squared distribution
[SSE
u
(SSE
A
SSE
B
SSE
C
)]/ (2J 2)
(SSE
A
SSE
B
SSE
C
)]/(n 3J)
[SSE
C
(SSE
A
SSE
B
SSE
C
)]/ 2J
(SSE
A
SSE
B
SSE
C
)]/(n 3J)
c04.qxd 8/27/2004 2:49 PM Page 153

154 MULTIPLE REGRESSION WITH CATEGORICAL PREDICTORS
with G 1 degrees of freedom. Two points should be noted. First, Barlett’s test is
very sensitive to departures from normality, so if the errors are not normally distrib-
uted, the test may not be accurate. Second, C is always greater than 1, so if the term
inside the parentheses in the expression for B is already under the critical chi-
squared value for testing at level α, it is not necessary to calculate C—the null
hypothesis will not be rejected either way. If the term inside the parentheses is
greater than the critical chi-squared value, it is necessary to calculate C and do the
complete computation for B (Neter et al., 1985). Examples are given in the exercises.
EXERCISES
4.1 In the couples dataset, 189 couples have no children, and 227, or 54.57%, of
couples have children. For all 416 couples, the mean couple-conflict score is
1.79, with a standard deviation of .601384. Couples without children have a
mean conflict score of 1.5658 with a standard deviation of .480. Couples with
children have a mean conflict score of 1.9759, with a standard deviation of
.629. If a dummy variable, PRESCHDN, is created with those having children
the interest category and those without children the contrast group, then:
(a) Give the sample equation for the SLR of couple conflict on PRESCHDN.
(b)Give r and r
2
for the SLR of couple conflict on PRESCHDN.
(c) Test whether there is a significant relationship between couple conflict
and having children using the two-sample t test, the test for the
significance of r, and the test for the dummy coefficient (i.e., t d/σ
ˆ
d
). In
so doing, you should find that all three t tests are equivalent. (Hint: See
Exercise 4.25 for helpful ideas on this problem.)
4.2 For the 416 couples in the couples dataset, a regression of couple conflict on
a dummy variable OWNKID, representing all children in the household being
the natural children of both partners, and a dummy variable STEPKID, rep-
resenting at least one child being a stepchild (“no children” is the omitted
group) produced the following equation:
yˆ 1.5723 .4023 OWNKID .3866 STEPKID.
The variance–covariance matrix of parameter estimates is:
OWNKID STEPKID
OWNKID .00365
STEPKID .00171 .00711
RSS is 16.3622 and SSE is 133.7280.
(a) Give the mean couple conflict for the three groups of couples.
(b) Test whether there is a significant relationship between child type and
couple conflict.
c04.qxd 8/27/2004 2:49 PM Page 154
