Alfred DeMaris - Regression with Social Data, Modeling Continuous and Limited Response Variables
Подождите немного. Документ загружается.


someone is on graduate faculty. For example, the expected difference in salary for
someone in “firelands” versus someone in “arts and sciences” is δ
1
γ
1
GRAD.
Therefore, it is δ
1
if someone is not on graduate faculty and δ
1
γ
1
if they are. Once
again, if γ
1
equals zero, the difference in mean salaries between “firelands” and “arts
and sciences” is the same whether or not one is on the graduate faculty.
Test for Interaction. If all of the gammas in equation (4.3) equal zero, there is no
interaction between college and graduate faculty status in their effects on mean
salary. This can be tested using the nested F test, since setting all of the gammas to
zero in equation (4.3) results in the simplified model of equation (4.2). Hence, the
model in (4.2) is nested inside the model in (4.3). Model 4 in Table 4.3 presents sam-
ple estimates for the model in equation (4.3), along with the results of the nested F
test. As is evident in the table, the nested F statistic (shown as “∆F” in the table) is
7.151. With 4 and 715 degrees of freedom, this is a highly significant result
(p .0001). It appears from tests of the individual gammas that there are two
significant interactions: between GRAD and BUSINESS and between GRAD and
OTHER. Let’s interpret the overall interaction effect using GRAD and college alter-
nately, as the focus variables. With GRAD as the focus, its partial effect is
10879 4426.179 FIREL 12874 BUSINESS
2144.285 EDUCATN 6515.672 OTHER.
The overall interpretation of this effect is that being on the graduate faculty seems to
be worth an increase in average salary for all faculty, but the extra amount is great-
est for the Business College and smallest for those in “other departments.” For
example, the increment due to being on graduate faculty for the Business College
is 10879 12874 23753, whereas for those in “other” departments, it is only
10879 6515.672 4363.328.
If college is the focus, the partial effects are:
Firelands: 486.301 4426.179 GRAD.
Business: 4093.737 12874 GRAD.
Education: 2298.292 2144.284 GRAD.
Other: 454.592 6515.672 GRAD.
Once again, the overall interpretation is that Firelands and Business faculty make, on
average, lower salaries than Arts and Sciences faculty if they do not have graduate
faculty status, but more if they do. On the other hand, those in “education” and those
in “other departments” make, on average, less than Arts and Sciences faculty if they
are not on the graduate faculty, and considerably less if they are. We must keep in
mind, however, that only two of the gammas are significant, so some of these appar-
ent differences do not necessarily hold in the population.
In contrast to the estimates in model 3 of Table 4.3, those for model 4 will per-
fectly (within rounding error) reproduce the cell means in Table 4.1. Why? Notice
MODELS WITH EXCLUSIVELY CATEGORICAL PREDICTORS 135
c04.qxd 8/27/2004 2:49 PM Page 135

that there are 10 cells in Table 4.1, each containing a mean salary that is independ-
ent of the other means. Hence there are 10 independent pieces of information, or
degrees of freedom, in this table. Model 4 uses 10 parameters, an intercept and nine
regression coefficients, to explain these 10 observations. In terms of the means (but
not the individual faculty members), model 4 is saturated. That is, there are as many
parameters as observations. Whenever this occurs, the model will perfectly repro-
duce the sample observations, which in this case refer to the cell means. As an exam-
ple, consider using models 3 and 4 in Table 4.3, the main effect and interaction
models, to predict average salary for those in the Business College with graduate
faculty status. According to Table 4.1, the sample mean salary for these faculty is
60250.92. Model 3’s prediction is 40348 11188 5512.28 57048.28, which is
off by about $3000. Model 4’s prediction is 40593 10879 4093.737 12874
60252.26, which, within rounding error, is the correct value.
MODELS WITH BOTH CATEGORICAL AND
CONTINUOUS PREDICTORS
Typically, in regression models we have a mix of both categorical and continuous
predictors. If there is no interaction between the categorical and continuous regres-
sors, these models are equivalent to ANCOVA models. The idea in ANCOVA is to
examine group differences in the mean of Y while adjusting for differences among
groups on one or more continuous variables, called covariates, that also affect the
dependent variable. We want to see how much group membership “matters,” in the
sense of affecting the response variable, after taking account of group differences on
the covariates. “Taking account,” of course, means holding the covariates constant,
or treating the groups as though they all had the same means on the covariates.
For simplicity’s sake, let’s assume that we have a categorical predictor, Z, with
categories A, B, and C, and one continuous covariate, X. Then letting C be the ref-
erence group for Z, and letting A and B be dummy variables for being in categories
A and B, respectively, the regression model for Y is
E(Y) β
0
δ
1
A δ
2
B β
1
X. (4.4)
Figure 4.1 shows how this model can be interpreted. To begin, the model can be
expressed for each group separately, by substituting the values for each dummy into
equation (4.4). Hence, for group C the equation is
E(Y) β
0
δ
1
(0) δ
2
(0) β
1
X β
0
β
1
X, (4.5)
for group A we have
E(Y) β
0
δ
1
(1) δ
2
(0) β
1
X β
0
δ
1
β
1
X, (4.6)
136 MULTIPLE REGRESSION WITH CATEGORICAL PREDICTORS
c04.qxd 8/27/2004 2:49 PM Page 136
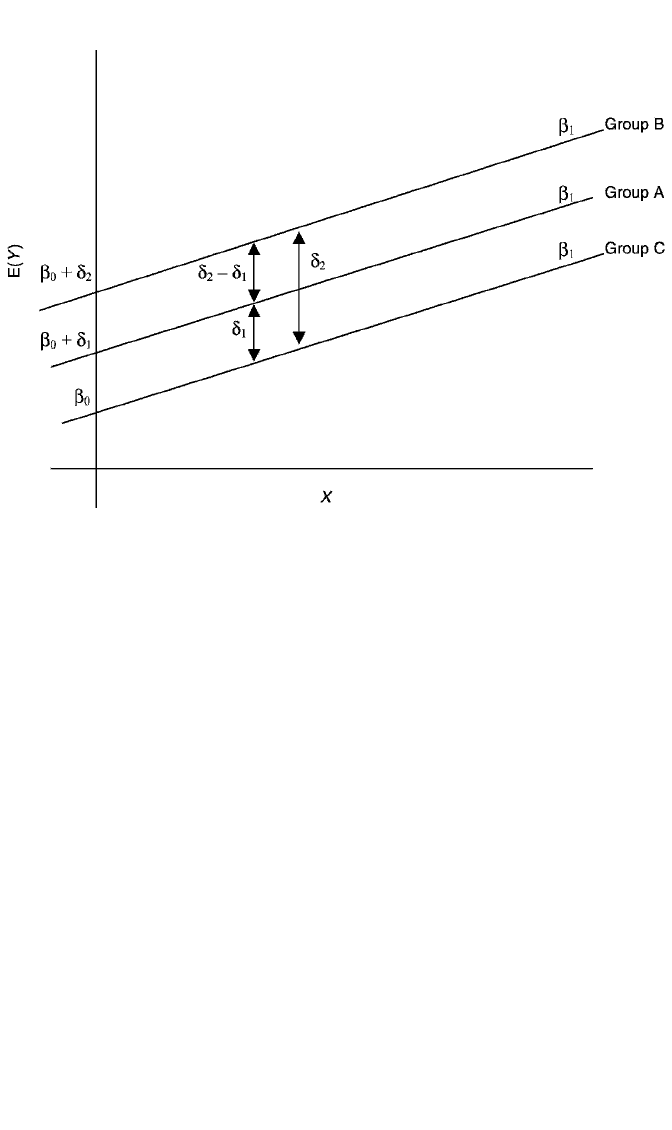
and for group B we have
E(Y) β
0
δ
1
(0) δ
2
(1) β
1
X β
0
δ
2
β
1
X. (4.7)
These three equations are essentially simple linear regressions of Y on X in which
the equation for each group has a different intercept but a common slope of β
1
.
Due to the common slope, the regression lines are parallel. This condition is
depicted in the figure. For group C, the regression of Y on X has intercept β
0
and
slope β
1
. For group A, the intercept is β
0
δ
1
, and the slope is β
1
. For group B, the
intercept is β
0
δ
2
and the slope is β
1
. Hence, controlling for Z, the impact of X is
constant; that is, the effect of X is the same in each group. On the other hand, δ
1
,
δ
2
, and δ
2
δ
1
represent constant differences in the mean of Y across groups
regardless of the level of X. This can easily be verified by taking differences
between equations (4.5) to (4.7). For example, the difference in the mean of Y for
groups A and C is
E(Y 冟A) E(Y 冟C) β
0
δ
1
β
1
X (β
0
β
1
X) δ
1
,
for groups B and C we have
E(Y 冟B) E(Y 冟C) β
0
δ
2
β
1
X (β
0
β
1
X) δ
2
,
MODELS WITH BOTH CATEGORICAL AND CONTINUOUS PREDICTORS 137
Figure 4.1 Regression model E(Y) β
0
δ
1
A δ
2
B β
1
X, depicting the absence of interaction between
the categorical variable, Z, and the continuous variable, X.
c04.qxd 8/27/2004 2:49 PM Page 137

and for groups A and B we have
E(Y 冟B) E(Y 冟A) β
0
δ
2
β
1
X (β
0
δ
1
β
1
X) δ
2
δ
1
.
In other words, the deltas and their difference represent group differences in the
mean of Y after adjusting for the covariate. In the figure, these differences are
depicted as two-headed arrows. Notice that these group differences in E(Y ) are the
same all along the range of X. This is an artifact of the model, since it does not allow
for interaction between X and Z.
Adjusted Means
When interest centers on differences in the mean of Y across groups, we often want
to examine mean differences both before and after adjusting for one or more covari-
ates. Actually, the adjusted mean differences themselves—the differences between
the adjusted means—are represented by the deltas in equation (4.4). But we may
want to present both unadjusted (disregarding any covariates) and adjusted (control-
ling for covariates) means, in order to highlight variability in group means both
before and after controlling for one or more continuous predictors. The idea behind
adjusted means is that we statistically “force” the groups to all have the same mean
on the covariate(s). How? We simply choose a value for each covariate and evaluate
the model at that value or values. It is customary to choose the sample mean of the
covariate as the control value. Thus, for the model in equation (4.4), the equation for
the adjusted mean of Y is
E(Y) β
0
δ
1
A δ
2
B β
1
x
苶
.
The equations for the adjusted means of each group are
C: E(Y) β
0
β
1
x
苶
.
A: E(Y) β
0
δ
1
β
1
x
苶
.
B: E(Y) β
0
δ
2
β
1
x
苶
.
By taking differences among these three equations, the reader can verify that the
adjusted mean differences are, in fact, δ
1
, δ
2
, and δ
2
δ
1
. The method is easily
extended to the case of multiple covariates: We simply substitute each covariate’s
mean into the equation and then evaluate the equation for the different groups to pro-
duce the adjusted means for each group.
Faculty Salary Example. Table 4.5 presents ANCOVA models for faculty salary
regressed on the dummies representing college, plus four centered covariates: years
in rank, years at BG (referred to in Chapter 3 as “years at the university”), prior
experience, and marketability. In Table 3.4 we saw that these covariates are impor-
tant predictors of salary. Model 1 in that table is reproduced as model 1 in Table 4.5
138 MULTIPLE REGRESSION WITH CATEGORICAL PREDICTORS
c04.qxd 8/27/2004 2:49 PM Page 138

(although the intercepts are different, since not all of the covariates were centered in
Table 3.4). It shows the results of salary regressed on the four centered covariates.
Although years in rank is not significant, the other three covariates all have sig-
nificant, positive effects on salary. If the distributions of these covariates are sub-
stantially different across colleges, it is important to adjust for them in any analysis
of the effect of location in a particular college of the university on salary. Otherwise,
we will have a misleading picture of the extent to which salary differences across
colleges are due to college per se rather than to key covariates which happen to differ
for each college. Table 4.6 shows the means on the four covariates both overall and
by each college.
The variability in the means reveals that the distributions on these four covariates
do, in fact, change considerably across colleges. Compared to the overall mean for
years in rank, “arts and sciences,” “education,” and “other departments” are above
average on years in rank, while “firelands” and “business” are below average. In that
years in rank is not a significant predictor of salary, however, these differences may
not be of consequence. Differences on the other three covariates, on the other hand,
could be important. “Arts and sciences” and “other departments” are above average
in years at BG, whereas “firelands,” “business,” and “education” are below average.
In terms of prior experience,“firelands” and “education” stand out as being substan-
tially above average, while “business” has the lowest mean on this factor. Finally,
marketability shows an interesting pattern in which the mean for the Business College
is not only above average but is substantially higher than the marketability scores for
MODELS WITH BOTH CATEGORICAL AND CONTINUOUS PREDICTORS 139
Table 4.5 Models for Academic Year Salary Regressed on College Plus Covariates
for Number of Years in Rank, Number of Years at BG, Prior Experience, and
Marketability for 725 Faculty Members
Adjusted
Mean
Predictor Model 1
a
Model 2
a
Model 3
b
Salary
Intercept 47801.000*** 47950.000*** 46993.000*** 47950.000
Firelands 6098.382*** 5142.106*** 41851.618
Business 4444.926*** 5401.202*** 52394.926
Education 1507.845 551.569 46442.155
Other 1620.079 663.803 46329.921
Years in rank
c
121.466 137.728 137.728
Years at BG
c
1072.730*** 1093.968*** 1093.968***
Prior experience
c
924.893*** 952.136*** 952.136***
Marketability
c
35001.000*** 27020.000*** 27020.000***
SSE 57048547616 54259263744 54259263744
F 267.218*** 144.298*** 144.298***
R
2
.598 .617 .617
a
Uses dummy coding.
b
Uses effect coding.
c
Centered variable.
* p .05. ** p .01. *** p .001.
c04.qxd 8/27/2004 2:49 PM Page 139

any of the other colleges. In that marketability has a strong impact on salary, one
would expect that controlling for this covariate should reduce the gap in salary
between “business” and the other colleges.
Model 2 in Table 4.5 shows the ANCOVA model for salary regressed on the col-
lege dummies plus the four covariates. Is college’s effect on salary significant after
controlling for the covariates? That is, does the addition of the four dummies repre-
senting college make a significant contribution to the model? We answer this ques-
tion using the nested F test, since model 1 is nested inside model 2. The test statistic,
using the R
2
values from the two models, is
F
(.
(
6
1
1
72
.6
17
.5
2
9
)/
7
7
5
1
)
6
/4
9.212.
With 4 and 716 degrees of freedom, this is a very signficant result (p .00001). We
can conclude that at least one of the dummy coefficients is nonzero. Or more gener-
ally, we can conclude that at least one of the mean contrasts in salary between col-
leges is nonzero. We see that two coefficients are significant: the mean difference
between “firelands” and “arts and sciences” and the mean difference between “busi-
ness” and “arts and sciences.” The other two coefficients, contrasting “education” and
“other departments” with “arts and sciences,” are nonsignificant. Recall from model 1
in Table 4.3 that all of the coefficients reflecting contrasts with “arts and sciences”
were significant when the covariates were ignored. Thus, some of the effects of
college on salary have been accounted for by adjusting for differences across colleges
in key predictors of salary. This is highlighted further by the fact that the dummy
coefficients representing mean differences across colleges have all been reduced in
magnitude compared to model 1 in Table 4.3. For example, the unadjusted mean
difference in salary between “firelands” and “arts and sciences” is 8645.202. The
adjusted mean difference is now 6098.382. So a little over $2500 in the average
salary difference between “firelands” and “arts and sciences” is due to differences
between these colleges in average years in rank, years at BG, prior experience,
140 MULTIPLE REGRESSION WITH CATEGORICAL PREDICTORS
Table 4.6 Means for the Covariates Years in Rank, Years at BG, Prior Experience,
and Marketability: Overall and by College of the University for 725 Faculty Members
at BGSU
Covariate
Years Years Prior
College in Rank at BG Experience Marketability
Arts and Sciences 7.880 13.777 2.973 .935
Firelands 5.486 10.514 3.143 .955
Business 5.843 9.304 2.069 1.159
Education 7.456 11.778 3.656 .865
Other 7.725 12.603 2.756 .830
Overall 7.397 12.530 2.899 .940
c04.qxd 8/27/2004 2:49 PM Page 140

MODELS WITH BOTH CATEGORICAL AND CONTINUOUS PREDICTORS 141
and marketability. The same comment can be made regarding the other coefficient
reductions.
Model 3 in Table 4.5 is the same as model 2 except that effect coding is used to
represent colleges. In comparison to model 2 in Table 4.3, we see that the departures
of each college’s mean salary from the grand mean are smaller than was the case
without controlling for covariates. Moreover, whereas three of these departures were
significant before, only two are significant now. To further foreground the closing of
the salary gaps across colleges, the last column of Table 4.5 shows the adjusted mean
salaries for each college after accounting for the four key covariates. Because the
covariates are centered and their means are therefore all zero, calculating adjusted
means is quite straightforward. One just ignores the coefficients for the covariates in
model 2 in Table 4.5 and uses the intercept and dummy coefficients to calculate the
means. For example, the adjusted mean for “arts and sciences” is just the intercept
in model 2—47950. The adjusted mean for “firelands” is 47950 6098.382
41851.618, and so on. It is evident that compared to the unadjusted means for each
college in the last column of Table 4.1, the adjusted means exhibit less variability.
Mean Contrasts with an Adjusted Alpha Level. Recall that with five categories of
the variable college, there are 10 possible mean salary contrasts between pairs of col-
leges that can be tested. Up until now, I have been conducting these tests without
controlling for the increased risk of type I error—or capitalization on chance—that
accrues to making multiple tests. There are several procedures that accomplish this
control; here I discuss one, the Bonferroni comparison procedure. The Bonferroni
technique is advantageous because of its great generality. It is not only limited to
tests of mean contrasts. It can be used to adjust for capitalization on chance when-
ever multiple tests of hypothesis are conducted, regardless of whether or not they are
the same type of test. The rationale for the procedure is quite simple. Suppose that I
were making 10 tests and I wanted my overall chance of making at least one type I
error to be .05 for the collection of tests. That is, I want the probability of rejecting
at least one null hypothesis that is, in fact, true, to be no more than .05 over all tests.
If I make each test at an α level of .05, the probability of making a type I error on
each test is .05. This means that the probability of not making a type I error on any
given test is .95, and the probability of not making any type I errors across all 10
tests is therefore (.95)
10
.599. This implies that the probability of making at least
one type I error in all these tests is 1 .599 .401. In other words, we have about a
40% chance of declaring one H
0
to be false when it is not. The Bonferroni solution
in this case is to conduct each test at an α level of .05/10 .005. This way, the prob-
ability of not making a type I error on any given test is .995, and the probability of
making at least one type I error across all 10 tests is 1 (.995)
10
.049. In general,
if one is making K tests and one wants the probability of making at least one type I
error to be held at α across all tests, the Bonferroni procedure calls for each test to
be made at an α level of α α/K.
Although the Bonferroni procedure has the advantages of simplicity and flexi-
bility, it tends to be somewhat low in power. Holland and Copenhaver (1988) discuss
several modifications of the Bonferroni procedure that result in enhanced power to
c04.qxd 8/27/2004 2:49 PM Page 141

142 MULTIPLE REGRESSION WITH CATEGORICAL PREDICTORS
detect false null hypotheses. The one I focus on here is due to Holm (1979). The
Bonferroni–Holm approach is to order the attained p-values for the K tests from
smallest to largest. One then compares the smallest p-value to α/K. If p α/K, one
rejects the corresponding null hypothesis and moves to the test with the next small-
est p-value. This is compared to α/(K 1). If this p is less than α/(K 1), one
rejects the corresponding null hypothesis and moves to the test with the next small-
est p-value, which is compared to α/(K 2). We continue in this fashion, each time
comparing the next smallest p-value to α/(K 3), then to α/(K 4), and so on,
until the largest p-value is compared to α/1 α. As long as the p-value for the
given test is smaller than the relevant adjusted α level, the corresponding null
hypothesis is rejected and we continue to the next test. If, at any point, we fail to
reject the null, testing stops at that point and we fail to reject all of the remaining
null hypotheses.
Table 4.7 presents tests for mean salary differences between colleges after adjust-
ing for years in rank, years at BG, prior experience, and marketability, using
Bonferroni–Holm adjusted α levels (shown as α in the table). The tests are based
on the dummy coefficients in model 2 in Table 4.5. The adjusted α levels are .05/10
.005, .05/9 .0056, .05/8 .0063, and so on, so that the last adjusted α level is .05.
The first seven contrasts are all significant since the p-value for each of the tests is
less than the adjusted α level. However, we fail to reject equality of mean salaries
for “other departments” versus “arts and sciences,” hence we fail to reject equality
of the last two contrasts as well. The outcomes of these tests are the same as would
have been realized if we had simply used the .05 α level for each test. However, this
procedure, unlike that simpler one, holds the overall α level down to .05. Notice that
the unmodified Bonferroni procedure, using α .005 for each test, would have
failed to reject equality for the “other departments” versus “firelands” and the “edu-
cation” versus “firelands” contrasts. That they are rejected under Bonferroni–Holm
reveals the greater power of the latter procedure.
Table 4.7 Tests for Mean Salary Differences between Colleges after Adjusting
for Years in Rank, Years at BG, Prior Experience, and Marketability, Using
Bonferroni–Holm Adjusted
αα
Levels (Based on Model 2 in Table 4.3)
Mean Salary
Contrast Difference p α
Business–Firelands 10543.000 .0001 .0050
Other–Business 6065.005 .0001 .0056
Firelands–A&S 6098.382 .0001 .0063
Education–Business 5952.772 .0001 .0071
Business–A&S 4444.926 .0002 .0083
Other–Firelands 4478.303 .0086 .0100
Education–Firelands 4590.537 .0092 .0125
Other–A&S 1620.079 .0850 .0167
Education–A&S 1507.845 .1508 .0250
Other–Education 112.233 .9254 .0500
c04.qxd 8/27/2004 2:49 PM Page 142

Interaction between Categorical and Continuous Predictors
The ANCOVA model, together with adjusted means, makes sense only if the differ-
ences in group means are the same at different values of the covariate (or at different
values of the covariate patterns exhibited by the continuous regressors). In this case
it makes sense to speak of group mean differences that exist after adjusting for
the covariates—treating group differences as constant regardless of the levels of the
covariates. If this condition is not met, we have statistical interaction between the
continuous and categorical predictors. In this section of the chapter, I discuss this
type of interaction and show how it can be interpreted with, alternately, the continu-
ous and the categorical variable as the focus.
Interaction Model. For simplicity, once again, I explicate interaction with a model
that has one categorical predictor, Z, with three categories—A, B, and C (the refer-
ence category)—and one continuous predictor, X. This time, I allow Z to interact
with X in its impact on Y. The model is
E(Y ) β
0
δ
1
A δ
2
B β
1
X γ
1
AX γ
2
BX. (4.8)
To interpret the interaction effect, let’s write the simple linear regression of Y on X
separately for each group. For group C the equation is
E(Y ) β
0
β
1
X, (4.9)
for group A it is
E(Y ) β
0
δ
1
(β
1
γ
1
)X, (4.10)
and for group B we have
E(Y ) β
0
δ
2
(β
1
γ
2
)X. (4.11)
We can see immediately that the regression of Y on X has a different slope in each
group. Thus, if X is the focus, its impact is β
1
in group C, β
1
γ
1
in group A, and β
1
γ
2
in group B. That is, the effect of X changes across groups. If the gammas both turn out
to be zero, there is no difference in the effect of X in each group. The Y-intercepts for
each group are, once again, β
0
for group C, β
0
δ
1
for group A, and β
0
δ
2
for group
B. Figure 4.2 illustrates the model for the three groups.
If group is the focus, we ask how group differences might depend on the level of
X. To ascertain this, we take differences between equations (4.9) to (4.11). The
difference in the mean of Y for group A vs. group C is (4.10) (4.9), or
E(Y 冟A) E(Y 冟C) β
0
δ
1
β
1
X γ
1
X β
0
β
1
X δ
1
γ
1
X.
MODELS WITH BOTH CATEGORICAL AND CONTINUOUS PREDICTORS 143
c04.qxd 8/27/2004 2:49 PM Page 143
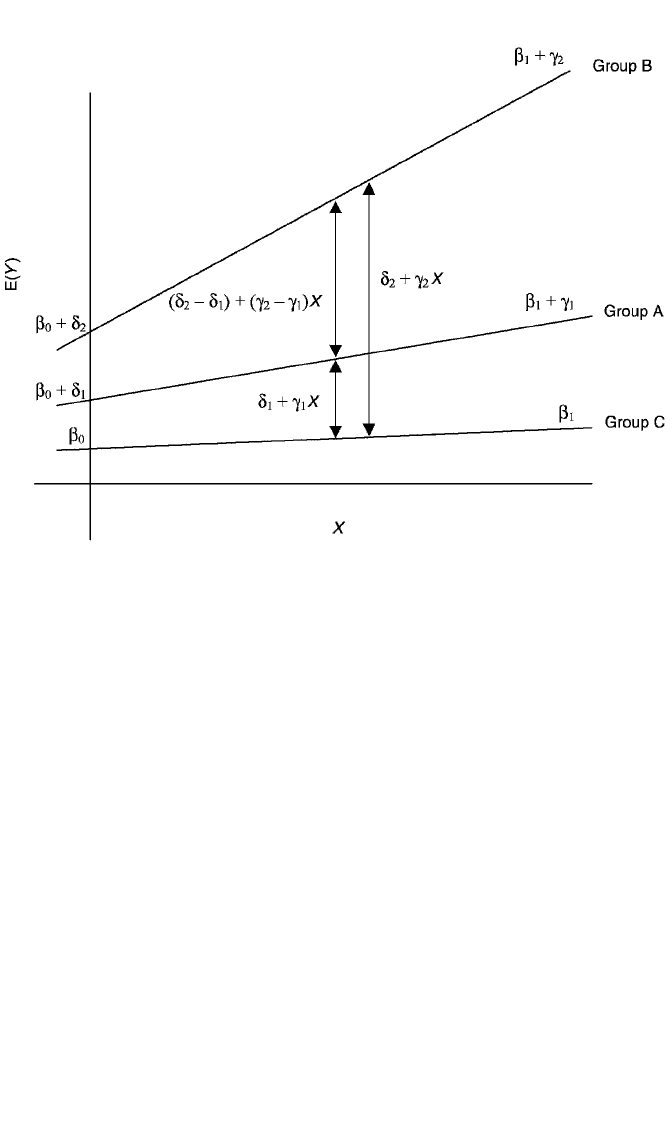
The difference in means for groups B and C is (4.11) (4.9), or
E(Y 冟B) E(Y 冟 C) β
0
δ
2
β
1
X γ
2
X β
0
β
1
X δ
2
γ
2
X.
Finally, the difference in means for groups B and A is (4.11) (4.10), or
E(Y 冟B) E(Y 冟 A) β
0
δ
2
β
1
X γ
2
X β
0
δ
1
β
1
X γ
1
X
(δ
2
δ
1
) (γ
2
γ
1
)X.
It is evident here that group differences in the mean of Y are no longer constant as
they were in the no-interaction model. Instead, they are a function of the level of X.
Figure 4.2 depicts this situation by showing that the gap between any two groups’
means increases as we go from lower to higher values of X. This particular model is
designed to exhibit interaction that is ordinal in both X and Z. With respect to the
effect of X, this means that the direction of its impact (which in this example is pos-
itive) is the same in each group but that the magnitude of its effect changes across
groups. Similarly, that the interaction is ordinal in Z is illustrated by the fact that
although the gap between groups’ means gets larger with increasing X, the ordering
of group means is always the same: The mean for group B is always higher than the
mean for group A, which is always higher than the mean for group C.
144 MULTIPLE REGRESSION WITH CATEGORICAL PREDICTORS
Figure 4.2 Regression model E(Y) β
0
δ
1
A δ
2
B β
1
X γ
1
AX γ
2
BX, depicting ordinal interac-
tion between the categorical variable, Z, and the continuous variable, X.
c04.qxd 8/27/2004 2:49 PM Page 144
