Alfred DeMaris - Regression with Social Data, Modeling Continuous and Limited Response Variables

Подождите немного. Документ загружается.

A second-order interaction eﬀect among, say, X, Z, and W in their eﬀects on Y would

be modeled by including the following predictors in the model: X, Z, W, XZ, XW, ZW,

and XZW. The equation would then be

E(Y) ⫽ β

⫹ β

X ⫹ β

Z ⫹ β

W ⫹ β

ZW ⫹ γXZ ⫹ λXW ⫹ δXZW

Factoring the common multipliers of X, we have

E(Y) ⫽ β

⫹ β

Z ⫹ β

W ⫹ β

ZW ⫹ (β

⫹ γZ ⫹ λW ⫹ δZW )X

Now the partial slope for X is β

⫹ γZ ⫹ λW ⫹ δZW. This is an interaction model

in the variables Z and W. Thus, the model suggests that the impact of X on Y is a

function of the interaction of Z with W; or, the extent to which Z moderates the

impact of X on Y itself depends on the level of W. It should be apparent that higher-

order interactions become increasingly unwieldy to understand, let alone model. As

one rarely encounters the modeling of interactions any higher than ﬁrst-order [see

MacDonald and DeMaris (2002) for an exception, however], they will not be con-

sidered further here [but for a lucid discussion of higher-order interaction eﬀects, see

Aiken and West (1991)]. The partial slope of X in the ﬁrst-order interaction model

has a unit-impact interpretation, just like the eﬀect of X in the no-interaction, or main

eﬀects, model. It reﬂects the expected change in Y for a unit increase in X (in

Exercise 3.19 I ask you to prove this). It is also the ﬁrst partial derivative of equation

(3.9) with respect to X.

Ordinal versus Disordinal Interaction. Let’s consider some examples of interaction

models. Suppose that the equation is E(Y) ⫽ 5 ⫹ .2X ⫹ 1.5Z ⫹ .05XZ, where X ranges

from 0 to 10 and Z ranges from 0 to 5. Then the partial slope for X is .2 ⫹ .05Z. Thus,

when Z is 0, the partial slope for X is .2. When Z is 2.5, the partial slope for X is

.2 ⫹ .05(2.5) ⫽ .325. When Z is 5, the partial slope for X is .2 ⫹ .05(5) ⫽ .45. In this

case, X always has a positive eﬀect on Y, but the magnitude of the eﬀect is stronger at

higher values of Z. This type of interaction is called an ordinal interaction (Kerlinger,

1986): The eﬀect of X changes in magnitude, but not direction, with changing values

of Z. But suppose that the equation is E(Y) ⫽ 5 ⫹ .2X ⫹ 1.5Z ⫺ .1XZ, with X and Z

being the same as before. In this equation, the partial slope for X is .2 ⫺ .1Z. Now,

when Z is 0, the partial slope for X is .2. However, when Z is 2, the partial slope for X

is .2 ⫺ .1(2) ⫽ 0; and when Z is 5, the partial slope for X is .2 ⫺ .1(5) ⫽⫺.3. In this

case, the eﬀect of X changes direction over values of Z, resulting in a disordinal inter-

action (Kerlinger, 1986). Note that the only real way to ascertain whether the interac-

tion is ordinal or disordinal within the observed range of the moderator variable is to

calculate some sample values of ps

over diﬀerent values of Z, and see whether ps

changes sign across these values. (Technically, the terms ordinal and disordinal refer

to whether the slopes for the regression of Y on X cross when plotted according to

diﬀerent values of Z. However, even if the lines do not cross within the observed range

of Z, I refer to the interaction as disordinal if the slope changes from positive to nega-

tive, or vice versa, over values of Z.)

EMPLOYING MULTIPLE PREDICTORS 105

c03.qxd 8/27/2004 2:48 PM Page 105

Centering, Revisited. In Exercise 2.6 I introduced the term centered variable, refer-

ring to a variable that is deviated from its mean. Centered variables are particularly

useful in interaction models. Consider equation (3.9) again. Suppose that zero is not

a legitimate value for Z. Then the t test for b

—the main eﬀect of X—is not particu-

larly meaningful since it refers to the eﬀect of X when Z is zero. Similarly, the test for

refers to the eﬀect of Z when X is zero, which, again, may not be a meaningful

value for X. However, if Z and X have ﬁrst been centered, and the cross-product XZ is

constructed using the centered variables, the main eﬀects of X and Z are always mean-

ingful. The reason for this is that a centered variable, say Z

⫽ Z ⫺ Z

苶

, has a mean of

zero. Therefore, the main eﬀect of X, β

, in the centered-variable interaction model is

the eﬀect of X when Z

is zero or when Z is at its mean. The same interpretation

applies to the main eﬀect of Z if X is also centered: It is the eﬀect of Z when X is at

its mean. Hence, centering in interaction models renders the main eﬀects of the inter-

acting variables interpretable. Another advantage of centering variables involved in

interactions has to do with the problem of multicollinearity (discussed below). Recall

that multicollinearity arises because one variable is highly correlated with another

variable or with a linear combination of the other variables. Cross-product terms of

the form XZ are highly correlated with their component variables—X and Z—and

therefore introduce collinearity problems into the model. It turns out that centering

variables before creating cross-product terms brings about a substantial reduction in

this collinearity [see Aiken and West (1991) for the mathematics behind this].

Example. Table 3.4 presents a MULR analysis of faculty salary for 725 faculty

members at Bowling Green State University (BGSU) for the academic year 1993–

1994. The dependent variable is the nine-month salary in dollars. The independent

variables are the number of years of prior experience ( job experience prior to start-

ing at BGSU), the number of years at the university, the number of years in rank, and

a continuous variable tapping the marketability of one’s discipline. This marketabil-

ity factor is the ratio of average academic-year salary of full-time faculty in a partic-

ular discipline to average academic-year salary of all full-time faculty. The variables

years at the university and years in rank are both centered. Model 1 is the main eﬀects,

or additive model, the model without any interaction eﬀects. All variables except

years in rank have signiﬁcant eﬀects on salary. The directions of eﬀects suggest that

years of prior experience, years at the university, and marketability of the discipline

are all positively associated with salary. Although the marketability variable appears

to have the largest unstandardized eﬀect, the standardized coeﬃcients suggest that

years at the university has the strongest impact on salary.

Model 2 investigates the interaction of years at the university with years in rank in

their eﬀects on salary. Therefore, model 2 adds to the main eﬀects model the cross-

product of centered years at the university with centered years in rank. The coeﬃcient

for the interaction eﬀect is signiﬁcant at p ⬍ .05, suggesting that the impact of years

at the university is a function of years in rank. To ascertain the nature of the interac-

tion, we examine the partial slope for years at the university. Its value is (1008.267 ⫺

15.481 years in rank). In that the main eﬀect of years at the university is signiﬁcant,

we see that years at the university has a signiﬁcant positive eﬀect on salary for those

106 INTRODUCTION TO MULTIPLE REGRESSION

c03.qxd 8/27/2004 2:48 PM Page 106

who are average in the number of years in rank. In particular, for these faculty, each

year longer that they have been at the university is estimated to be worth $1008.27

additional salary, on average. However, this eﬀect grows slightly weaker the longer

someone has been in rank. For example, for someone who is 1 standard deviation, 7.043

years, above mean years in rank, the eﬀect of years at the university is 1008.267 ⫺

15.481(7.043) ⫽ 899.234. Thus, for someone this long in rank, each additional year

at the university is only worth an additional $899.23 of salary. The most likely expla-

nation of this eﬀect is that years in rank is an inverse proxy for productivity. That is,

the most productive faculty tend to be promoted sooner, all else equal. Therefore, a

greater number of years in rank tends to be associated with lower productivity. Finding

that years at the university has a weaker eﬀect the longer one has been in rank sug-

gests that seniority has a weaker eﬀect on salary for the relatively less productive.

As mentioned, the fact that the main eﬀect of years at the university is signiﬁcant

suggests that this factor is signiﬁcant for those who are average in years in rank.

Suppose that we wish to know whether years at the university is signiﬁcant among all

those who are 1 standard deviation above mean years in rank. At this point, some

clariﬁcation is in order. In the sample regression equation, yˆ ⫽ b

⫹ b

X ⫹ b

Z ⫹ gXZ,

a signiﬁcant coeﬃcient, g, for the cross-product XZ, does not imply that the impact of

X is signiﬁcant at a particular level of Z. In fact, the eﬀect of X may not be signiﬁcant

at any level of Z, even though g is signiﬁcant. The signiﬁcance of g means only that

EMPLOYING MULTIPLE PREDICTORS 107

Table 3.4 Regression Models for Faculty Salary for 725 Faculty Members, Showing

First-Order Interaction of Years at the University with Years in Rank

Model 1 Model 2

Regressor bb

Intercept 12219.000*** .000 13241.000*** .000

Years of prior 924.893*** .317 906.418*** .311

experience

Years at the 1072.730*** .759 1008.267*** .713

university

Years in rank

⫺121.466 ⫺.061 37.996 .019

Marketability of 35001.000*** .372 34948*** .372

discipline

Years at the ⫺15.481* ⫺.074

university ⫻

years in rank

RSS 84691222609.000 85141325670.000

MSE 79234093.911 78718281.718

F 267.218*** 216.319***

.598 .601

adj

.595 .598

Centered variable.

Cross-product of centered variables.

* p ⬍ .05. ** p ⬍ .01. *** p ⬍ .001.

c03.qxd 8/27/2004 2:48 PM Page 107

we can reject the null hypothesis that γ⫽ 0. In that γ captures the variation in ps

over

levels of Z, rejection of this null hypothesis only suggests that ps

varies with Z,

not that ps

is diﬀerent from zero at any particular level of Z. To answer the latter

question, we must test the signiﬁcance of b

⫹ gZ at a given level, z, of Z. The test

statistic is

t ⫽

ᎏ

⫹

ᎏ

where σ

⫹ gz

is the estimated standard error of b

⫹ gz. Under H

: β

⫹ γ z ⫽ 0, this sta-

tistic has the t distribution with n ⫺ K ⫺ 1 degrees of freedom. The standard error is

just the square root of the variance of b

⫹ gz. The expression for the variance of b

⫹ gz

can be found using covariance algebra. Assuming that Z is ﬁxed over repeated sam-

pling, we have

V(b

⫹ gz) ⫽ Cov(b

⫹ gz, b

⫹ gz)

⫽ Cov(b

) ⫹ zCov(b

,g) ⫹ zCov(b

,g) ⫹ z

Cov(g,g)

⫽ V(b

) ⫹ 2zCov(b

,g) ⫹ z

V(g). (3.10)

In model 2, let X be years at the university, Z be years in rank, b

be the main eﬀect

of years at the university, and g be the coeﬃcient for the interaction of years at the

university with years in rank. From the variance–covariance matrix of parameter

estimates for model 2 (not shown), the relevant estimates are 5145.182 for V(b

41.913 for V(g), and 174.527 for Cov(b

,g). At one standard deviation (7.043 years)

above mean years in rank, the estimated variance of ps

is therefore 5145.182 ⫹

2(7.043)(174.527) ⫹ 7.043

(41.93) ⫽ 9682.615. The estimated standard error of ps

is the square root of this, 98.4. The test statistic for the signiﬁcance of years at the

university at this level of years in rank is therefore

t ⫽

ᎏ

⫽ 9.139.

With 719 degrees of freedom, this is a highly signiﬁcant result ( p ⬍ .00001).

Problems with Cross-Product Terms. In addition to the collinearity created by

cross-product terms, two other diﬃculties can arise when investigating interaction

eﬀects. First, researchers examining interaction eﬀects using nonexperimental data

may often ﬁnd these terms to be nonsigniﬁcant. Or, if signiﬁcant, they may turn out

to account for very little variance in the criterion. McClelland and Judd (1993) dis-

cuss the reasons for this. They point out that it is the residual variation in XZ—the

unique variance not shared with the other predictors in the model—that determines

the statistical power of the test for addition of the XZ term. Moreover, the residual

variance of XZ is determined entirely by the joint distribution of X and Z. The more

correlated X is with Z, the greater the power for detecting interaction eﬀects. What

is needed, in particular, is an “optimal” distribution of X and Z in which “extreme

108 INTRODUCTION TO MULTIPLE REGRESSION

c03.qxd 8/27/2004 2:48 PM Page 108

values of X co-occur with similarly extreme values of Z” (McClelland and Judd,

1993, p. 384). Controlled experimentation allows the researcher to arrange X and Z

so that this type of distribution occurs. However, with nonexperimental data, there is

no guarantee that the joint distribution of X and Z will be optimal. McClelland and

Judd (1993) therefore advise nonexperimental data analysts to temper their expecta-

tions regarding the sizes of interaction eﬀects in their analyses, and to regard more

modest eﬀects as equally important. This should be the case especially when inter-

actions are guided by strong theory.

The other diﬃculty is that nonlinearitiy in the relationship between a regressor and

the criterion can frequently be confused with an interaction eﬀect. In particular, when

the relationship between X and Y is quadratic in nature—the true model has Y as a

function of X and X

(Chapter 5 considers such models at length)—such an eﬀect

may masquerade as an interaction. The reason for this is that the reliability of X

lower than the reliability of XZ when X and Z are highly correlated (McCallum and

Mar, 1995). Since unreliability attenuates true eﬀects, it is likely that spurious mod-

erator eﬀects will override real quadratic eﬀects in the data when the true model is

quadratic. McCallum and Mar (1995) demonstrate this phenomenon using extensive

simulations. They advise that the best strategy is to have a compelling theoretical or

substantive rationale for preferring one type of model over the other. In a similar vein,

Ganzach (1997) argues that researchers investigating interaction eﬀects of the form

XZ should always include X

and Z

in the model, and vice versa. He demonstrates

using empirical examples that if this strategy is not followed, the nature of interaction

or quadratic eﬀects found in the sample will often be biased. Again, the best strategy

is to have a sound theoretical rationale before investigating any such more complex

eﬀects in the data.

Multicollinearity. I indicated above that the creation of cross-product terms—or

quadratic terms, for that matter—induces collinearity problems. Collinearity that

results from the creation of special terms to capture interaction or nonlinear eﬀects

is known as nonessential ill-conditioning. Collinearity due to high correlations

among naturally occurring variables, on the other hand, is referred to as essential ill-

conditioning (Aiken and West, 1991). In either case, multicollinearity can pose prob-

lems in data analysis that the researcher needs to be aware of. The two major

consequences that interfere with good parameter estimation are (1) the variances of

parameter estimates become greatly inﬂated, causing wide ﬂuctuations in the values

of estimates from sample to sample; and (2) the magnitudes of parameter estimates

are substantially inﬂated, making it appear that variables have much stronger eﬀects

than they really have. There are some well-known symptoms associated with

collinearity, which the researcher should learn to recognize. One symptom is a very

signiﬁcant F test or high R

value in combination with the ﬁnding that no individual

coeﬃcients are signiﬁcant. However, as noted above, this may also be due to the fact

that some complex linear combination of the parameters is what is driving the F or R

results. Other symptoms are parameter estimates that are unreasonably large in mag-

nitude or have counterintuitive signs, standard error estimates that are especially

large, or standardized coeﬃcients that are outside the range of [⫺1, ⫹1].

EMPLOYING MULTIPLE PREDICTORS 109

c03.qxd 8/27/2004 2:48 PM Page 109

The best single diagnostic for detecting multicollinearity is the variance inﬂation

factor for the kth coeﬃcient, denoted VIF

. This measure is deﬁned as

VIF

⫽

ᎏ

1 ⫺ R

冟x

⫺k

ᎏ

, (3.11)

where R

冟x

⫺k

is the R

for the regression of X

on all other X’s in the model. The

denominator of equation (3.11), called the kth variable’s tolerance, represents the pro-

portion of variation in X

not shared with all other X’s. Tolerances smaller than .1, or

equivalently, VIF’s greater than about 10 suggest that collinearity is beginning to be a

problem in one’s analysis (Myers, 1986). This is also somewhat dependent on sample

size, with larger samples better able than smaller ones to tolerate collinearity. As an

example, the VIF’s for model 2 in Table 3.4 range from 1.007 for marketability of dis-

cipline to 5.822 for years in rank. What can be done about collinearity? One remedy for

nonessential collinearity is to center variables before creating cross-products or poly-

nomial terms, as indicated above. This reduces the estimated standard errors for all

terms except the highest-order cross-product or polynomial term (Aiken and West,

1991). For collinearity among naturally occurring variables, there are some simple

options. First, if two variables are very highly correlated, consider dropping one of them

from the model. If most of the variance of one variable is shared with the other, not

much more information is gained by including the second one in the model. Or if two

or more items are highly correlated because they are measuring the same underlying

construct, consider incorporating them into a single scale. Another remedy when X and

Z are highly correlated is to substitute ln X and ln Z for X and Z in the model since the

nonlinear transformation of the natural log reduces the degree of correlation (which

only taps linear association). More elaborate remedies are discussed in Chapter 6.

Comparing Models across Groups. A variant on the interaction theme is the situation

in which the model as a whole might be diﬀerent for diﬀerent groups. For example, does

the same salary model characterize both male and female faculty? One could argue that

they should not, for either of two reasons. First, in the United States, women have his-

torically been paid less for doing the same work. One might therefore expect that such

factors as the number of years at the university or marketability of the discipline may

not have as strong an eﬀect on salary for women as they do for men. This would be the

gender bias hypothesis. On the other hand, given the concern with gender equity in pay

that has characterized the American workplace over the past 25 years or so, one might

expect the opposite. That is, women may be more highly rewarded for seniority or for

marketability of discipline than men are, to make up for past injustices. This would be

the reverse discrimination hypothesis. Table 3.5 explores this issue by presenting salary

model 2 from Table 3.4 separately for male and female faculty.

There are some notable diﬀerences. To begin, the intercepts are diﬀerent, with the

male intercept being about $2500 higher than the female intercept. The intercepts are

not entirely interpretable because zero is not a plausible value for marketability of the

discipline. Nevertheless, this diﬀerence suggests that for those with no prior experience,

who are average in years at the university and years in rank, and who are in a discipline

with zero marketability, males make $2500 more than females. Additionally, years of

110 INTRODUCTION TO MULTIPLE REGRESSION

c03.qxd 8/27/2004 2:48 PM Page 110

experience and marketability of discipline have stronger eﬀects on salary among males,

as suggested by the gender bias hypothesis, whereas years at the university has a

stronger eﬀect among females, as suggested by the reverse discrimination hypothesis.

Also, the interaction of years at the university with years in rank is only signiﬁcant for

females. [No substantive implications should be drawn from this analysis, since it

excludes several key factors in the determination of salary. For a complete assessment

of potential gender discrimination in salary at BGSU, see Balzer et al. (1996) or

Boudreau et al. (1997).]

To assess whether the models are truly diﬀerent for each group, we can perform

a Chow test (Chow, 1960). If we let p equal K ⫹ 1, the number of parameters in the

model, c denote the model estimated for the combined sample (i.e., model 2 in Table

3.4), and m and f denote models for males and females, respectively, the test statis-

tic has the form

F ⫽

Under the null hypothesis that the same model applies to each group, this statistic

has the F distribution with p and n ⫺ 2p degrees of freedom. Now, SSE for the

combined analysis is 56598444555. Hence, for the current problem we have

F ⫽⫽10.703.

[56598444555 ⫺ (40991619682 ⫹ 10930510277)]/6

ᎏᎏᎏᎏᎏᎏ

(40991619682 ⫹ 10930510277)/(725 ⫺ 12)

[SSE

⫺ (SSE

⫹ SSE

)]/p

ᎏᎏᎏ

(SSE

⫹ SSE

)/(n ⫺ 2p)

EMPLOYING MULTIPLE PREDICTORS 111

Table 3.5 Regression Models for Faculty Salary for 511 Male Faculty Members and

214 Female Faculty Members

Male Model Female Model

Regressor bb

Intercept 17402.000*** .000 14954.000*** .000

Years of prior

experience 1020.899*** .370 370.365** .156

Years at the

university

929.251*** .674 1100.884*** .896

Years in rank

93.937 .049 ⫺245.221 ⫺.142

Marketability of 33303.000*** .367 26883.000*** .346

discipline

Years at the ⫺14.936 ⫺.068 ⫺22.298* ⫺.164

university ⫻

years in rank

SSE 40991619682.000 10930510277.000

F 135.154*** 45.185***

.572 .521

Centered variable using separate means by gender.

Cross-product of centered variables.

* p ⬍ .05. ** p ⬍ .01. *** p ⬍ .001.

c03.qxd 8/27/2004 2:48 PM Page 111

With 6 and 713 degrees of freedom, this result is quite signiﬁcant ( p ⬍ .00001).

Apparently, the dynamics of salary determination work diﬀerently for males than

they do for females.

EVALUATING EMPIRICAL CONSISTENCY

In this ﬁnal section of the chapter, I discuss ways of evaluating the empirical con-

sistency of the MULR model. As an example, I evaluate the full model (model 3) of

exam scores for 214 students, which was presented in Table 3.1. Recall that in chap-

ter 2 I presented a formal test for empirical consistency for SLR: Neter et al.’s (1985)

lack-of-ﬁt test. This test was based on the ratio of MSLF, the mean of the sum of

squares for lack of ﬁt, to MSPE, the mean of the sum of squares for pure error. The

same test applies in MULR, except that SSPE is based on the sum of squared devi-

ations of the individual Y-values around the group mean of the Y’s at each covariate

pattern in the data. As before, SSLF ⫽ SSE ⫺ SSPE. The test again employs an F sta-

tistic of the form

F⫽

ᎏ

The degrees of freedom for this statistic are now n ⫺ c and c ⫺ p, where p ⫽ K ⫹ 1 is

the number of parameters in the model and c is the number of diﬀerent covariate pat-

terns in the data. SSPE can still be recovered in SAS using PROC RSREG. However, a

problem in MULR with continuous independent variables is that there will usually be

as many diﬀerent covariate patterns as there are cases. In this event, SSPE is necessar-

ily zero, and the test is of no utility. This is, in fact, the case for model 3 in Table 3.1.

There are 214 cases and 214 diﬀerent covariate patterns in the data. (The number of

diﬀerent covariate patterns can easily be counted by counting the number of diﬀerent

predicted values there are in the data, since each diﬀerent covariate pattern results in a

unique predicted value.)

Examination of Residuals

Lacking a formal test of empirical consistency, we can always resort to more infor-

mal methods. One such technique employed in Chapter 2 was an examination of

the raw and standardized residuals for potential outliers, nonconstant variance, or

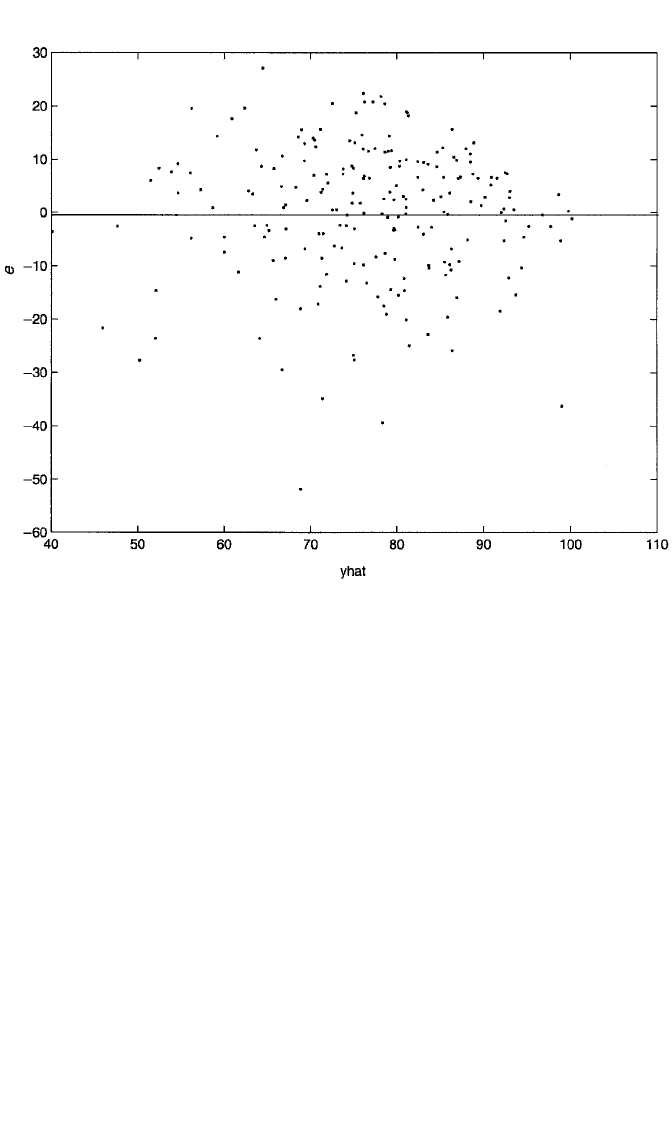
nonlinearities. Figure 3.8 shows a plot of the raw residuals against yˆ for model 3.

The plot appears to have the desired shape, a band of points spread evenly around

the line e⫽ 0. There does not appear to be any noticeable nonlinearity in the rela-

tionship between e and yˆ, nor does the trend in the points suggest any dramatic

variation in the variance of the residuals across yˆ-values. For the detection of out-

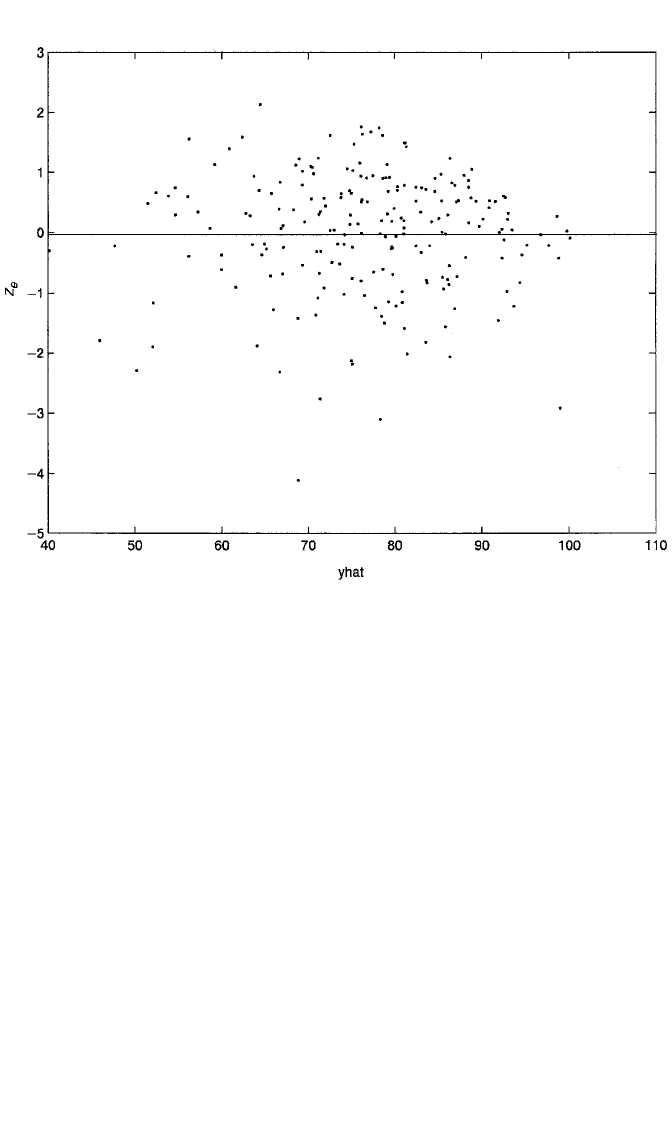
liers, it is better to plot the standardized residuals against yˆ. Figure 3.9 shows such

a plot. The plot looks pretty much the same except that the values of z

are much

smaller than those of e. Outliers would be indicated by standardized residuals

greater than about 4 in absolute value. There is perhaps one such data point in the

112 INTRODUCTION TO MULTIPLE REGRESSION

c03.qxd 8/27/2004 2:48 PM Page 112

middle lower part of the plot, although its value is right around ⫺4. Were we con-

cerned about this data point, it could be investigated further. However, perhaps

more important, no single observation stands out as being dramatically diﬀerent

than the others.

Partial Regression Leverage Plots

In Chapter 2 we examined scatterplots of Y against a single X to ensure that the X – Y

relationship was linear. In MULR the assumption is that the relationship between Y

and each X

is linear at ﬁxed levels of the other predictors. This assumption is obvi-

ous from the regression equation itself. Assume, for the moment, that all X’s other

than X

are ﬁxed at the values x

, x

,...,x

k⫺1

, x

k⫹1

, x

k⫹2

,...,x

. Then the MULR

equation is

E(Y) ⫽ β

⫹ β

⫹

...

⫹ β

k⫺1

x⫺1

⫹ β

⫹

...

⫹ β

⫽ β

⫹ β

⫹

...

⫹ β

k⫺1

⫹ β

k⫹1

⫹

...

⫹ β

⫽ α⬘⫹β

EVALUATING EMPIRICAL CONSISTENCY 113

Figure 3.8 Plot of residuals against ﬁtted values for the regression of score on the ﬁrst exam on math

diagnostic score, college GPA, attitude toward statistics, class hours in the current semester, and number

of previous math courses.

c03.qxd 8/27/2004 2:48 PM Page 113

where

α⬘⫽β

⫹ β

⫹

...

⫹ β

k⫺1

⫹ β

k⫹1

⫹

...

⫹ β

This shows that at ﬁxed levels of all other regressors, Y is a simple linear function of

. If this is not the case, the appropriate model should contain either transforma-

tions of X

that make the relationship linear, or additional terms to model the non-

linearity (Chapter 5 takes up these issues in greater detail).

One way to examine whether the relationship between Y and each X

is linear,

controlling for all other regressors, is to look at the partial regression leverage plots,

or partial plots, of Y with each X in the model. These are scatterplots of Y against

each X

, where the inﬂuence of all other regressors has been partialed out of each

variable. Partialing out all other regressors involves removing the linear association

between the given variable and all other regressors. How is this accomplished?

Suppose that we wish to look at the partial plot for X

, controlling for X

, X

,...,

. First, we regress Y on X

, X

,...,X

and save the residuals. Call these e

y 冟 x⫺1

representing the residuals for the regression of Y on all X’s except (minus) X

. Then

regress X

on X

, X

,...,X

. Save these residuals and call them, correspondingly,

114 INTRODUCTION TO MULTIPLE REGRESSION

Figure 3.9 Plot of standardized residuals against ﬁtted values for the regression of score on the ﬁrst

exam on math diagnostic score, college GPA, attitude toward statistics, class hours in the current semes-

ter, and number of previous math courses.

c03.qxd 8/27/2004 2:48 PM Page 114