Алешин Г.В. Оценка качества информационно-измерительных систем

Подождите немного. Документ загружается.

161

7. Эффективность оптимизации тем выше, чем существенней разница в

указанных требованиях к шкалам, а также чем существенней разница между

используемым техническим решением и оптимальным.

8. Задача оптимизации измерителя с последовательными во времени шка-

лами и ее решение при заданном интервале измерений формально совпадает с

задачей оптимизации распределения амплитудно-частотного спектра многош-

кального периодического сигнала .

9. При равных требованиях к шкалам оптимальные рабочие частоты рас-

полагаются по закону геометрической прогрессии.

10. При равных и больших энергетических потенциалах шкал, число шкал

пропорционально отношению априорной неопределенности к требуемой апо-

стериорной в децибелах и обратно пропорционально эквивалентному энерге-

тическому потенциалу в децибелах.

11. Доказано, что при малой априорной неопределенности, обеспечиваю-

щей однозначные измерения, оптимальным является гармонический сигнал с

наибольшей рабочей частотой (несущей, частотой модуляции, частотой повто-

рения и т.д.).

12. Априорная неопределенность играет исключительно важную роль при

синтезе измерителя, поскольку от ее величины зависят результирующая точ-

ность измерений при заданной структуре измерителя, либо, наоборот, число

шкал зависит от частоты, энергетики при заданной требуемой точности оценки

параметра и априорной неопределенности.

13. Без учета априорной неопределенности РТС невозможно корректно

поставить задачу синтеза любого измерителя.

14. Платой за большую априорную неопределенность может быть много-

канальность и (или) большее время поиска, а также неоднозначность измере-

ний и в следствие этого - многошкальность и, наконец, худшая результирую-

щая точность измерений.

15. Большое число шкал не является оптимальным с точки зрения исполь-

зования суммарной энергии сигнала, особенно при сравнительно малом отно-

шении сигнал/шум q и коэффициенте b. Однако при большой априорной неоп-

ределенности оно может оказаться необходимым. Для каждого отношения сиг-

нал/шум q и коэффициента b существует оптимальное число шкал, при кото-

ром реализуется максимальная точность измерений при заданной априорной

неопределенности.

16. Если шкалы дорогостоящие, например отдельные РТС, то достигать

требуемой точности при заданной априорной неопределенности целесообразно

не увеличением максимальных рабочих частот и числа шкал n, а увеличением

энергетического потенциала q и коэффициента b.

17. Повышение требований к надежности оценки шкал (уменьшение пара-

метров) и увеличение рабочих частот шкал по своему действию на точность

оценки равносильно снижению энергетического потенциала шкал, что приво-

дит к существенному росту числа шкал, особенно при большом отношении ап-

риорной неопределенности к требуемой дисперсии измерений (рис. 6.1). При

162

заданном энергетическом потенциале шкал коэффициент использования частот

шкал равносилен по своему действию надежности измерений.

18. Случаи малых энергетических потенциалов шкал менее желательны,

чем у одношкальных измерителей, поскольку даже при большом числе шкал с

увеличением числа шкал сначала возрастает точность, а затем уменьшается

(пороговый эффект , усиленный делением энергии по шкалам (рис. 6.1).

19. Изложенные положения справедливы также для фазовых измерителей

других параметров.

К основным рекомендациям разработчикам фазометрических систем сле-

дует отнести:

− выбор оптимальных параметров РТС в соответствии с изложенными ре-

зультатами;

− стремление к некоторому увеличению (рис. 6.1) числа шкал (или средств)

по сравнению с существующим числом (n <= 6), поскольку для больших и

средних энергетических потенциалов q > 100 и для существующих требова-

ний к надежности оценок (b ≈ 1,2...) недостаточно полно используются ин-

формационные возможности многошкальных систем. Либо существует дру-

гая альтернатива: стремиться к уменьшению априорной неопределенности за

счет других средств, что позволит сократить число шкал и упростить аппара-

туру.

6.3. Оптимизация многошкального устройства оценивания запазды-

вания сигнала с учетом ограничения на общие ассигнования

В данном подразделе кроме влияния на критерий качества ряда рассмот-

ренных факторов учитывается также влияние ограничений по стоимости про-

изводства измерителя.

Сформулированный в подразделе 6.2 обобщенный показатель качества А

многошкального измерителя связывает в компактной канонической форме не-

сколько характеристик, называемых внешними параметрами, и внутренние па-

раметры. В нем отражены результирующая точность измерений

−2

, диспер-

сия априорного распределения

, коэффициенты доверия

k k

b( )

к оценкам

шкал, рабочие частоты шкал

, энергетические показатели - отношение сиг-

нал/шум q

и число шкал n

A b q b q

k k

= = + ≈

−

= =

∏ ∏

1 1

1( )

. (6.21)

Ограничения на пиковую мощность в передатчике, на общую длитель-

ность сигнала могут быть представлены как ограничения на результирующее

отношение сигнал/шум

163

q q

≤

∑

. (6.22)

Требуемый коэффициент доверия всего измерителя P(b),который называ-

ется также доверительной вероятностью,является также ограничением на ко-

эффициенты доверия шкал P(B

)

k k

b P

∏

≤

Ρ ( )

. (6.23)

Если шкалы однородные, где оценки в шкалах имеют одинаковую форму

плотности распределения вероятности, то

P b P b

k k k

( ) ( )=

Можно показать, что max A (6.21) при ограничении (6.23) достигается, ес-

ли

b b b

k k

= =

−1

По существу P(b) представляет собой вероятность отсутствия при измерениях

промаха, или непопадания в диапазон измеряемого параметра на всех шкалах.

Если приближение (6.21) несправедливо, то функция A не будет разделен-

ной (сепарабельной) по отношению к параметрам p и b. Решение такой задачи

сложней. Однако ее решение принципиально ничем не отличается от решения

задач, изложенных в разделах 4 и 5.

Решение задачи аналогично также в случае, если шкалы представляют со-

бой разнотипные измерители или системы с различными плотностями распре-

деления вероятности оценки. Во всех этих случаях в два этапа решается задача

оптимизации измерителя по параметрам q

и b

При построении систем всегда, хотя бы эвристически, учитывается стои-

мость ее создания и эксплуатации либо общая цена изделия. Если задача реша-

ется в интересах изготовителя системы, закупающего комплектующие детали,

то это цена изделия. Если все комплектующие изделия изготовляются тут же,

то это себестоимость. Как изложено в разделах 4, 5, задача может быть пред-

ставлена как задача выбора, если известны аналогичные образцы элементов

системы, их стоимости и параметры. Зависимости технических параметров от

стоимости могут быть представлены также в виде прогнозов или сглаженных

статистичексих данных, например в виде линий среднеквадратической регрес-

сии стоимости на параметры системы.

Таким образом, введем дополнительно ограничение на ассигнования на

измерительную систему. В соответствии с изложенным предполагается, что

имеется зависимость C

(q) или связь стоимости радиотехнической части систе-

мы с реализуемым ею отношением сигнал/шум

в каждой шкале.

Если шкалы принадлежат одной системе, то, как правило, стоимости их

одинаковы, а радиотехническая часть системы общая, или совмещенная.

Тогда задачу оптимизации такой системы с многошкальным измерителем мож-

но представить в виде

min min[ ( ]C C q) nC

= +

(6.24)

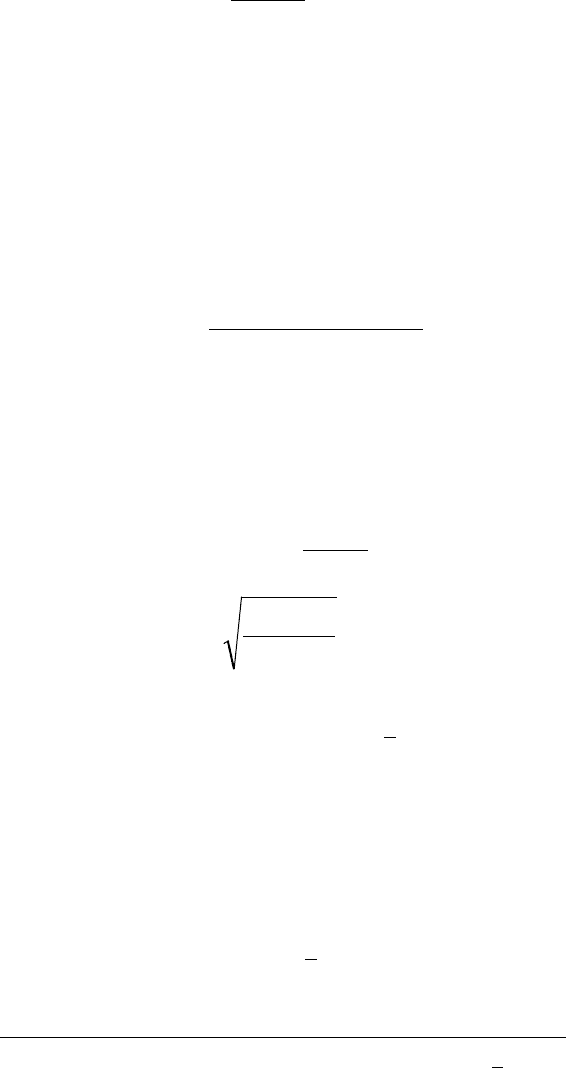
164

{ }

q n,

при ограничении

(1+ ≥bq) A

, (6.25)

где

nдо п

−

nдо п

- допустимая среднеквадратическая погрешность многошкального изме-

рителя, С - суммарная стоимость измерителя. Как и ранее, под стоимостью по-

нимается либо цена, себестоимость, стоимость производства, либо полная

стоимость. В любом случае ее значение для всех элементов системы должно

быть одно и то же.

Решение такой задачи математического программирования, сформулиро-

ванной в виде формул (6.24), (6.25) можно найти из уравнения

′

−

+ +

=C q)

C b A

bq) bq)

u q( )

(

( ln(

1 1

, (6.26)

которое получено при подстановке (6.25) в (6.24) и отыскании безусловного

экстремума.

Если сделать замену переменных:

X bq= +1

C q) C

u q u( )

( =

−













C A

то уравнение (6.26) можно преобразовать следующим образом

X k XC X

′

−

exp[ ( ( ))

Для дифференцируемых значений

С q)

u q( )

(

находим решение X

opt

данного

уравнения или уравнения (6.26) известным методом касательных, который на-

зывают еще методом Ньютона - Рафсона.

Приближенное решение отыскивается из итерационной формулы

k X C X X k X

k X k X C X

i u i i i

i i u i

′





















′

− −

−

− −

− − −

−

exp [ ( ( )) ][ ( )]

( )exp[ ( ( )) ]

1 1 1

1 2 1

2 1 1 1 1

где

165

k X

X C C X C

i i X X i X

i i i

2 1

1 1 1

( ) ( ) ( )

− −

−

′ ′

′′

− − −

Требуемое число шкал n

opt

определяется из формулы (6.25)

opt













ln( )1

где скобки

[ ]

означают целое большее число.

В общем случае, когда измеритель представляет собой не совмещенную

систему, а систему с раздельным приемом сигналов различных шкал, напри-

мер, измерительный комплекс с различными системами или многобазовую сис-

тему, то задача оптимизации может быть формализована в виде

min min [ ( ) ]C C q C

u k k

= +





















∑

(6.27)

при

( )1

+ =

∏

b q A

k k

. (6.28)

Можно показать аналогично [42], что для многобазовой системы, когда за-

висимости

С q)

(

одинаковые, при b

=b соотношения сигнал/шум в шкалах

тоже одинаковые. Для этих случаев задача (6.27), (6.28) упрощается

min min ( ]C n[C q) C

= +

{ }

q n,

при

(1+ =bq) A

Решение такой задачи находится из функционального уравнения

2 1

X X

C X

C X Cln

( )

Если зависимость

C q)

(

задана дискретными статистическими данными,

то такая задача формулируется как задача выбора функциональных элементов.

Если много таких элементов или параметров системы, то в соответствии с из-

ложенным в разделе 4 определяются линии среднеквадратической регрессии

стоимости на параметры. В любом случае существуют погрешности представ-

ления зависимостей

C q)

(

. Поэтому и решение не может иметь большую точ-

ность. Однако предложенный метод постановки и решения задач позволяет

найти интересующие в первую очередь точечные значения решений. Отыска-

ние доверительных границ решений здесь не рассматривается.

Введение дополнительных реально существующих ограничений уточняет

математическую модель эффективности систем, приводит, как и следует ожи-

166

дать, к ухудшению результата ее функционирования. Однако при этом стано-

вится небезразлично, как выбирать параметры систем, потому что появляются

оптимумы. Они появляются потому, что показатели качества систем между со-

бой противоречивы. Иными словами, улучшение одного показателя качества

может быть произведено лишь за счет ухудшения другого показателя при про-

чих равных условиях. Например, улучшение одного показателя качества поку-

пается ценой увеличения стоимости системы. Неиспользование возможности

оптимизации параметров систем может привести к существенному ухудшению

их показателей, даже если системы будут строить опытные эксперты. Оптими-

зация позволяет избежать существенных субъективных ошибок в построении

систем.

6.4. Общий случай оптимизации многошкальных измерительных сис-

тем

В данном подразделе приводится более общий случай оптимизации ра-

диотехнических систем: здесь будет учтено также ограничение на энергетиче-

ский потенциал радиолинии.

Задача (6.27, 6.28) может решаться только приближенно, если решение

существует и оно единственно. Для практически интересного случая, когда

С X( )

- монотонно возрастающая функция и

′

C X( )

>0,

C X

n( )

(

)

>0, методом

касательных можно получить итерационную формулу для расчета X

opt

C X C X C X

C C X

i i i i

i i i

+ +

′′

′

′′

−

− − −

[ ( ) ]ln

( )

1 1

1 1 1

, (6.29)

где

С C X

i i

− −

1 1

( )

Величина n

opt

определяется по формулам (6.18), (6.25). Алгоритм (6.29)

пригоден также для кривых с вогнутыми участками, если для

′′

≤

′













C X

C X C X

C X

C X C

u u

( ( ))

( ) ln

( ) ( )

1 2

. (6.30)

Рассмотрим условия применимости решения задачи для совмещенных

систем в качестве итеративных формул для определенного класса зависимостей

стоимость - энергетический потенциал. Используя принцип двойственности,

задачу

min min ( )C C q

u k

−

∑

(6.31)

при

( )1

+ ≥

∏

b q A

k k

(6.32)

можно записать в виде, аналогичном (4.7), (4.16), т.е.

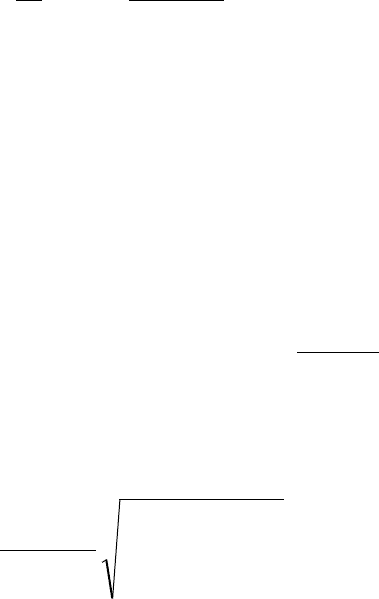
167

min min

1 1

∏

при

C (X ) C

2 k доп

k 1

≤

∑

∆

где

= +1 b q

k k

∆C C C

доп

= −

C X C arC

2 2 1

( ) [ ]=

−

Как показано в работе [42], такую задачу можно решить методом последо-

вательных приближений для широкого класса функций С(q

). Решение сущест-

вует, и оно единственно для выпуклых С

). Оно имеет вид

C X

A C X

kopt

′

∏

( )

Если условие (6.30) не выполняется, то используется итерационная проце-

дура для поиска оптимума [42].

Задача (6.31), (6.32) разрешима методом последовательных приближений

даже для более широкого класса функций, чем (6.30), однако, при этом необхо-

димо проверить абсолютность минимума. Исходя из изложенного выше, мож-

но установить, что для линейного сглаживания статистического материала

(стоимость-энегетический потенциал) задача решается точно,однако с методи-

ческой погрешностью, связанной с распределением вероятности выборок (ста-

тистического материала). Метод перебора вариантов построения возможен

лишь в случае, когда число “точек” невелико.

Для многошкальных систем эффективность также имеет форму (6.13).

Только из всего периодического выходного сигнала, представляющего собой

дискриминаторную характеристику, используется только полпериода, где со-

блюдается однозначность измерений. Иногда используется только часть полу-

периода, где точность измерений является приемлемой.

Таким образом, для многошкальных систем

A b q

k k

= +

∏

( )1

Поскольку качественная работа многошкальной системы возможна лишь

при

b q

k k

>>1, то

A K q

∏

168

где

K b

∏

n-число шкал.

Условия ограниченности энергии сигнала в шкалах, которые обусловлены

либо ограниченной пиковой мощностью сигнала, либо временем (длительно-

стью) сигнала, можно представить в виде ограничения на отношение сиг-

нал/шум

q q

∑

≤

∑

Условие ограниченности ассигнований С можно представить следующим

образом

[ ( ) ]C q C C

k k ok

+ ≤

∑

, (6.34)

где C

) -зависимость стоимости высокочастотной части системы от отноше-

ния сигнал/шум; C

- стоимость фазометрической аппаратуры шкалы.

Учитывая показатели качества (6.33), (6.34), задачу можно представить в

общем виде

min max

∏

(6.35)

при ограничениях

q q

∑

≤

∑

; (6.36)

[ ( ) ]C q C C

k k ok

+ ≤

∑

, (6.37)

где А

=А/К

Задача (6.35 – 6.37) отличается от (6.21), (6.22) дополнительным ограниче-

нием на ассигнования.

Это новое ограничение качественно меняет задачу, поскольку:

1)система функциональных ограничений может быть несовместной, т.е.

ограничения не удовлетворяются ни при каких значениях q

в шкалах; в этом

случае необходимо пересмотреть возможность реализации системы при задан-

ных q или C;

2) решение может не иметь экстремума, хотя оптимум (инфинум) может

быть;

3) если поменять местами целевую функцию и какое-либо ограничение, то

задача может иметь другое решение - это явление тоже есть один из типов

двойственности.

169

Проанализируем задачу для типичного случая обработки сигналов различ-

ными средствами в одном диапазоне

C q С q C q

k k k k k

( ) ( ) ( )= =

− −1 1

при одинаковой стоимости фазометрической части аппаратуры (шкалы)

C C

ok o

Тогда

[ (

) ] ( )C q C C q nC C

k k ok k o

+ = + ≤

∑

∑∑

. (6.38)

Если стоимость фазометрической части аппаратуры C

мала по сравнению

со стоимостью приемных трактов C(q

), то становится очевидным, что опти-

мальное решение задачи (6.35 – 6.37) совпадает с решением задачи оптимиза-

ции по критерию эффективности в смысле A при ограниченной мощности сиг-

нала

opt

∑

. (6.39)

Если условие (6.38) не выполняется, то при заданных ассигнованиях зада-

ча не имеет решения. Т.е., необходимо проверить выполнение условия (6.38).

Таким образом, при достаточно малом

C C q

o k k

<< ( )

или для

∀q

опти-

мальное решение равно (6.39), если выполняется условие (6.38). Оптимальное

число шкал определяется из условия

∂

ln ln

q n= − − =

∑

1 0

Если условие (6.38) выполняется для интервала значений n, то оптималь-

ное число шкал для задачи (6.35 – 6.37) выбирается из области допустимых

значений

n n n∈[ , ]

1 2

из соотношения (6.27), наиболее близких к n

opt

Выбор n может осуществляться определением n

или n

из уравнения

n[C

C C

( ) ]

∑

+ =

либо по итерационной формуле

n n

C q

K K C C q

i i

i i q12 1 1 1

, ( ) ( ) ( ) ( )

[ ]=

′

± −

′

− − −

∑

∑ ∑

где

C C

C q

i( )− −

′













∑

1 1

Для совмещенной измерительной системы условие (6.38) принимает вид

C q nC C

( )

∑ ∑

+ ≤

. (6.40)

В этом случае n

=0, а n

можно определить из уравнения, у которого обе

части соотношения (6.40) равны

170

C C q

−

∑

( )

Если

n n

opt2

,то

n n

opt2

, а если

n n

opt2

, то

n n:=

. В последнем случае

максимальная эффективность представляет собой supremum, а не экстремум.

Факт зависимости числа шкал и отношения сигнал/шум от стоимости от-

ражен как в условии (6.38), так и в (6.36). Если

n n

opt2

, то оптимальное от-

ношение сигнал/шум можно определить из уравнения

C C q

opt

= = −

−

∑ ∑ ∑

( )

, (6.41)

или по итерационной формуле, полученной методом касательных

C C q C q q

C q q

i i i

( )

( ) ( ) ( )

( )

( ) ( )

( )

∑

∑ ∑ ∑ ∑

∑

− +

′

− − −

−

1 1 1

Если

n n

opt2

≤

, то

C C q

( )

−

∑ ∑

откуда

C q

C n C C q C q q

i i

∑

∑ ∑ ∑ ∑

′

− − +

′

−

− −

2 0 1 1

( )

[ ( ) ( ) ]

( )

( ) ( )

Таким образом, в результате решения общей задачи оптимизации инфор-

мационно-измерительной радиотехнической системы могут быть получены оп-

тимальные внешние параметры, или показатели качества системы, и внутрен-

ние (технические) параметры, а также рекомендации об оптимальной структуре

системы и об оптимальном сигнале. Последнее в той степени, в какой структу-

ра и сигнал зависит от технических параметров. Для принятия решения о

структуре и сигналах необходимо также ставить задачу оптимизации

,используя те же показатели качества системы. Представленные алгоритмы

достаточно просты для использования. Решение задач оптимизации систем или

комплексов может служить промежуточным этапом, когда применяя результа-

ты решения задачи параметрического синтеза РТС, можно получить общее

(глобальное) решение, т.е. принять решение об элементах радиотехнических

систем или комплексов.

Приведенные результаты, учитывающие в общем случае априорную неоп-

ределенность, при обработке сигнала с целью измерения его параметра будут

использованы далее при рассмотрении многоэтапных систем. Многоэтапные

системы являются в некотором смысле наиболее общими системами, которые

могут включать в себя, в свои шкалы (этапы) все рассмотренные случаи. Не-

смотря на специфику построения шкал, методы принятия решения о много-

этапных системах, о числе шкал, об оптимальных параметрах шкал, об опти-