Алешин Г.В. Оценка качества информационно-измерительных систем

Подождите немного. Документ загружается.

141

адекватны. Определим

скр

. Если предположить сначала для простоты, что

в присутствии сигнала при его расстройке

X∆

по i-му параметру сигнала на

выходе приемника будет иметь место нормальный выходной эффект, то

скрытность

скр

по i-му параметру сигнала при известных других можно

определить следующим образом

скр

∆

, (5.69)

где D

- диапазон изменений i-го параметра.

Тогда общая скрытность будет равна

∏∏

∆

iскрскр

, (5.70)

где n

- число параметров настройки приемника. В приемнике сложных со-

ставных сигналов это могут быть: уровень сигнала (мощность р), уровень

спектральной плотности шума N(ω), задержка τ, частота настройки f, углы θ

и θ

, структура сигнала S(t) и т.д.

Нетрудно увидеть, что чем больше элемент настройки

X∆

по парамет-

ру Х

, тем меньше время поиска t

, однако меньше и скрытность сигнала

скр

, т.е., что скрытность и время поиска противоречивые критерии качест-

ва системы. Определим соотношение мопеду ними для рассмотренного слу-

чая с учетом упрощающего предположения об инвариантности времени на-

блюдения Т

оi

для любого элемента поиска ∆X

, что обычно имеет место в

достаточно широком диапазоне изменений параметра.

Тогда

∏

∆

, (5.71)

где

- априорный диапазон i-го параметра.

Оптимальное время поиска min t

следует определять при заданном

допскрскр

NN ≥

Таким образом

{ } { }

∏

∆∆

∆

Tmintmin

(5.72)

при

∏

≥

∆

допскр

. (5.73)

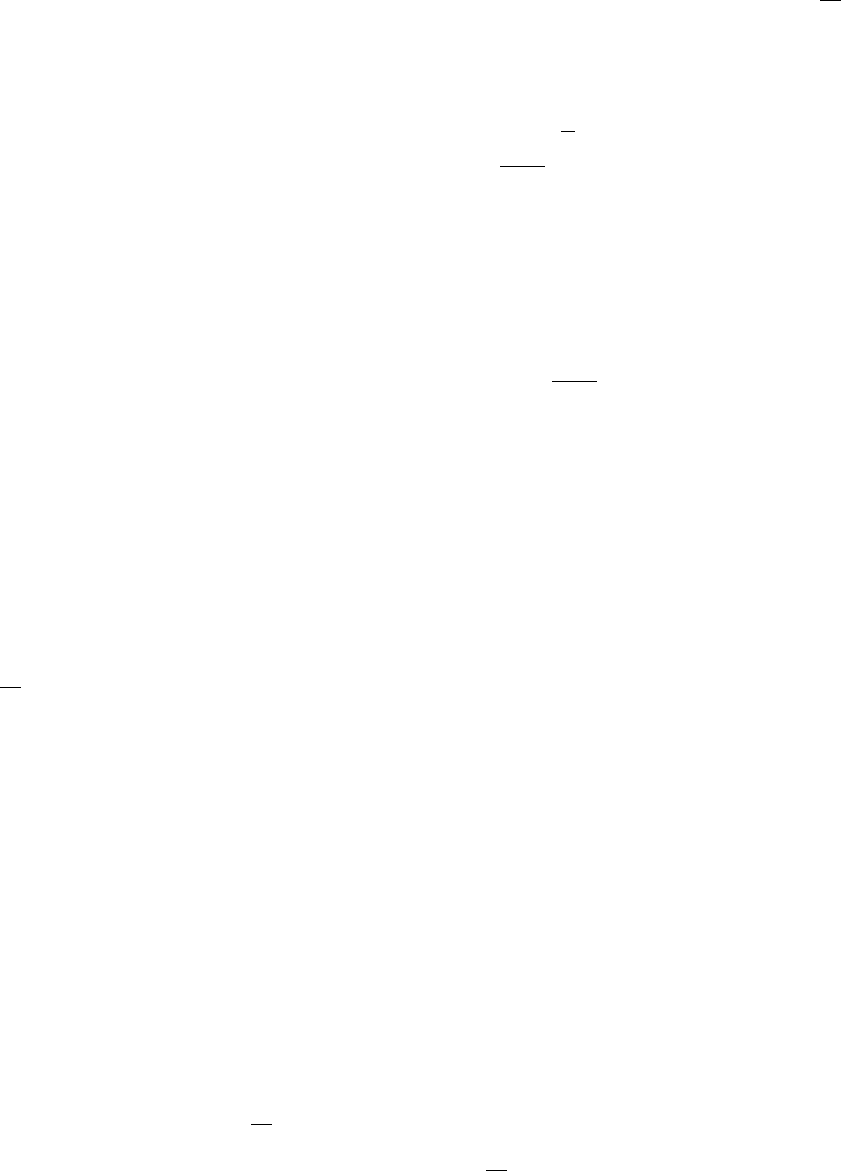
142

Нетрудно убедиться, что оптимум определяется на нижней грани нера-

венства (5.73). Но тогда время поиска t

инвариантно по отношению к

X∆

но прямо пропорционально скрытности. Действительно, из (5.70) и (5.71)

следует

{ }

∏

∆













допскр0n

NTtmin

. (5.74)

Из (5.74) следует естественный вывод о том, что время поиска сигнала

по n

параметрам для командно-измерительных систем пропорционально

скрытности и произведению отношении априорного диапазона поиска каж-

дого параметра своей системы по отношению к априорному диапазону поис-

ка сигнала разведывательной станции противника













Отдельно следует отметить особенности скрытности по структуре. О

ней можно говорить лишь тогда, когда осуществляется поэлементный прием

сигнала, разумеется с достаточной энергией каждого элемента, а для распо-

знавания сигнала учитывается вся совокупность элементов для принятия ре-

шения о сигнале. Прием сигнала "в целом" позволяет устранить скрытность

сигнала по задержке, если известна его структура, с помощью корреляцион-

ного приема и стробирования при фильтрационной обработке сигнала. Для

принятия. решения по критерию времени поиска об оптимальных расстрой-

ках

X∆

по искомым параметрам необходимо принять во внимание такие

ТТТ, как допустимые вероятности ложной тревоги и обнаружения. Согласно

ТТТ

( )

доплтT

FF ≤

(5.75)

( )

допобнобн

PP ≥ψ

, (5.76)

где ψ

пор

- пороговое значение функции неопределенности, соответствующее

верхней грани неравенства (5.76).

Таким образом

доплтFпор

Far

ЛТ

=ψ

, (5.77)

где

доплтFпор

Far

ЛТ

=ψ

- есть значение функции, обратной

доплт

, в точке

доплтлт

FF =

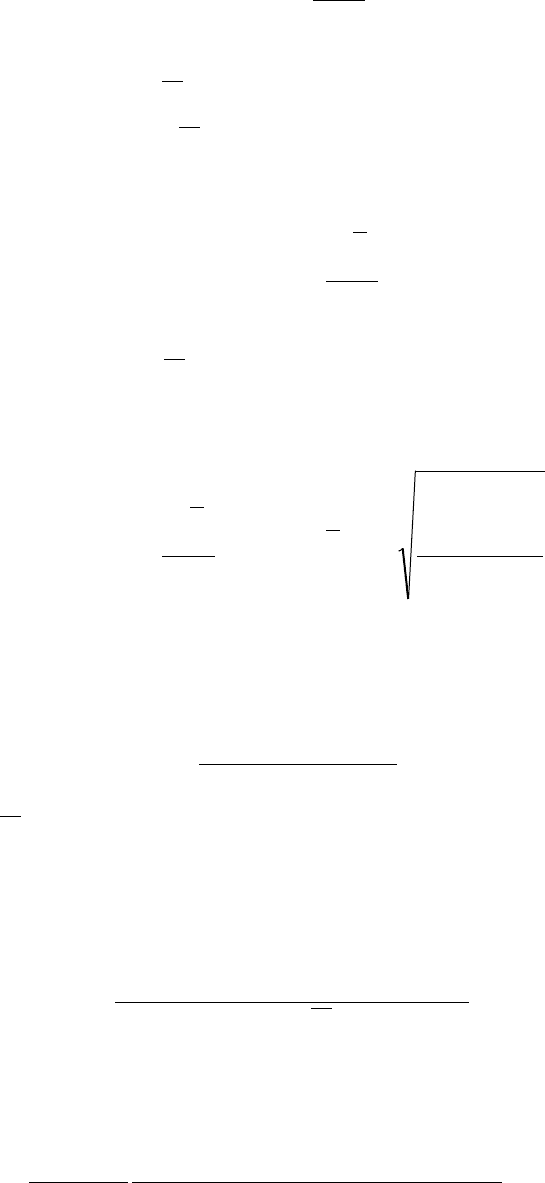
, А из неравенства (5.76) следует, что

( )

доплтFкорi

FarX

ЛТ

=ψ≥∆ψ

. (5.78)

Континуальное множество значений

X∆

, удовлетворяющих (5.78),

представляет собой по существу линии уровня функции неопределенности.

Если в системе требуется выполнение одного из требований к качественным

показателям (5.77), (5.79), то задачи могут быть сформулированы следующим

образом

143

{ } { }

∏

∆∆

∆

скр

maxNmax

(5.79)

при

( )

лтпорi

FX ψ≥∆ψ

( )

[ ]

допобнiобн

PXP ≥∆ψ

(5.80)

или

{ } { }

∏

∆∆

∆

Tmintmin

при

( )

лтпорi

FX ψ≥∆ψ

Задача (5.80) формально совпадает с рассмотренной в разделе 4. Действи-

тельно, задачу и ее решение можно представить в виде

{ } { }

0кор

nDT

Tmintmin

ψ−ψ

′

∆

∏

∏∏

∆∆

, (5.81)

при

( ) ( ) ( )

∑

ψ≥∆ψ

′

−ψ

лтпорix

FX00

(5.82)

( ) ( )

лтпор

opti

′

ψ−ψ

=∆

. (5.83)

Для вогнутых

( )

X∆ψ

решение (5.83) применимо как итеративное. Задача

(5.79) является тривальной, т.е. очевидно, что для выпуклой функции (5.79)

решение лежат на границе области определения. оно равно

{ }

( )











≠∆

∆ψ

′

∆∆ψ

′

−ψ−ψ

=∆=∆

∑

,1i minX

;1i

XminX

xпор0

optк

(5.84)

где

′

- самая меньшая из всех i крутизна в точке

( )

i10

XX ∆ψ∆

по оси X

( )

∏

∑

∆ψ

′

−ψ−ψ

′

∆

iXпор0

ckp

minX0

minX

Nmax

. (5.85)

Если система определяется такими допустимыми качественными пока-

зателями из состава ТТТ, как вероятность правильного обнаружения P

обн

. ве-

роятность ложной тревоги F

лт

, показатель скрытности – число комбинаций

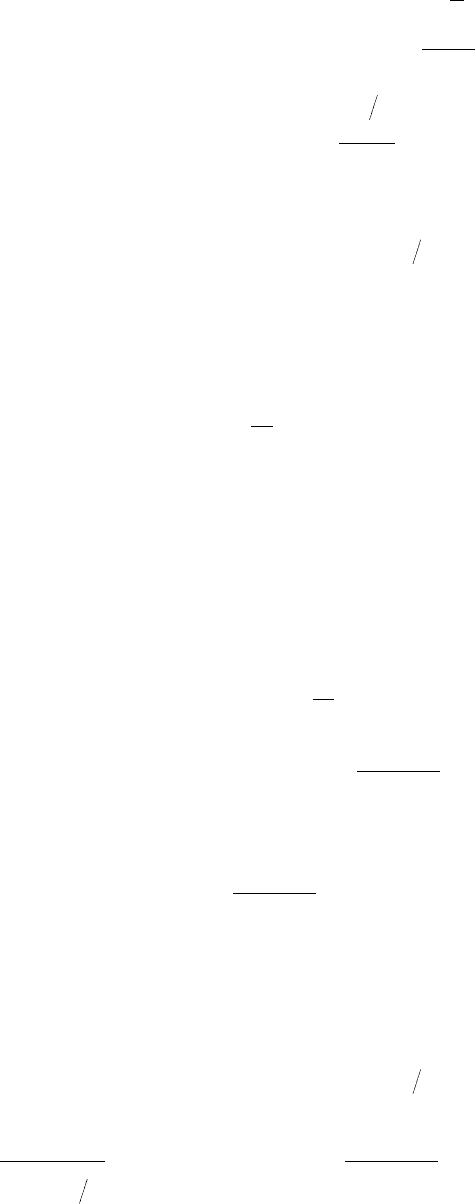
144

настройки для противника N

скр

и максимальное время последовательного по-

иска t

, то систему функциональных уравнений можно представить в виде

{ }

∏

∆

Tmintmin

; (5.86а)

∏

≥

∆

допскр

скр

; (5.86б)

( )

доп

пор

DD ψ≥ψ

; (5.86в)

iio

DXX ≤∆≤∆

. (5.87)

где ∆X

– минимально возможная расстройка по параметру, равная ширине

функции неопределенности по параметру или апертуре соответствующего

дискриминатора. Ограничение (5.88) ввиду монотонности кривой D(ψ), как и

в (5.79), (5.80) может быть представлена в виде

( )

лтпорi

FX ψ≥∆ψ

. (5.88а)

Если разложить (5.83а) в ряд Тейлора, то неравенство будет выглядеть иначе:

∑

∋

ψ∆≤∆ψ

′

, (5.88б)

где

( ) ( )

лтпор

F0 ψ−ψ=ψ∆

∋

(5.89)

Показатели (5.86) ввиду того. что варьируемыми являются лишь параметры

∆X

, можно записать параметры

X∆

, можно записать в более удобном виде

{ } { }

∏

∆

∋

∆

mintmin

; (5.90)

∋

≥

∆

∏

(5.91)

∑

∋

ψ≤∆ψ

′

; (5.92)

iio

DXX ≤∆≤∆

, (5.93)

где

∏∏

∋

допср

N ;

Физический смысл оптимальности решения многокритериальной задачи

(5.90)- (5.93) нетрудно проследить на трехмерном рисунке 5.3, для случая

145

двух параметров Х

и Х

. На рис. 5.3 изображена поверхность, задаваемая

критерием (5.90) и (5.92) (АВ). Оси координат для наглядности смещены на

X∆

по осям Х

и Х

и на величину

2010

∆∆

- по оси t

∋

. Верхнюю грань

ограничения (5.92) изображает плотность сечения АВСД, имеющая линию

пересечения с поверхностью (5.90) по кривой ДС. Отсюда видно, что совме-

стное решение (5.90), (5.92) отыскивается в плоскости АВСД в самой нижней

точке кривой ДС, поскольку это самый глубокий минимум t

(для усеченной

криволинейной пирамиды

∋

АВСД с вершиной

∋

) по всей области

определения (

ABX

) условного минимума t

. Множество

для (5.91) обо-

значим

. Ограничение (5.91) представляет собой пирамиду с той же

вершиной

∋

, но имеющую основание, соответствующее плоскости

JNI



параллельной плоскости

201

XXX

. Нижняя грань ограничения (5.91) или

площадь сечения N

∋

представляет собой множество оптимальных решений

для задачи из двух критериев (5.90), (5.91).

Рассмотрим, какой будет область допустимых решений и сами решения

для общей задачи (5.90 - 5.93). Ограничения (5.93) отображаются на рис. 5.3

отрезками

. Очевидно, что возможны три основных случая раз-

личных требований к скрытности, т.е. при различных N

∋

, например,

tmaxt

1n2

=≥

∋

по критерию (5.90) на верхней грани неравенства (5.92)

tmintN =≤

∋

для (5.90), (5.92) и промежуточный случай

3n1n

tNt ≤≤

∋

. В

первом случае, например, для N

∋2

область оптимальных решений

optxi

оп-

ределяется площадью

NJI

сечения (нижней гранью) критерия (5.91), кото-

рая полностью принадлежит области определения критерия, (5.92), т.е.

BXA

optx

MM ⊂

. Область допустимых решений M

в случае N

∋

представ-

ляет собой множество, ограниченное (5.91). В случае, когда

3n1n

tNt ≤≤

∋

например, для

∋∋

, нижняя грань критерия (5.91) станет усеченной

верхней гранью ограничения ( 5.92). Область оптимальных решений

optxi

принадлежит пересечению множеств, отображаемых проекцией на

201

XXX

сечением

333

JNI

∋

и треугольником AX

B, т.е.

( )

AXOBJNIoptx

MMM

∩⊂

∋

Область же допустимых решений M

представляет собой пространство,

ограниченное сверху поверхностью (5.90). Если

tN <

∋

, то очевидно, что

множество пересечений IN

∋

J и AX

B пусто, т.е.

=∩

∋ B

AXJIN

∅. Тогда

множество оптимальных решений М

xi opt

неизменно для

∋

∀N

и равно едино-

му элементу, определяемому

tmin

для (5.91), (5.92), так как

333

JNI

BXA

∋

⊂

. Область допустимых решений М

в этом случае лежит в

треугольнике

( )

BXA

xi0

MMBXA ⊂

. Очевидно, что для случая

tN ≥

∋

ко-

146

гда М

xi opt

(множество оптимальных решений) принадлежит множеству точек

кривой - FG, имеющуюся степень свободы в выборе

целесообразно ис-

пользовать для оптимизации системы по еще одному критерию дополни-

тельно, например, по стоимости. Рассмотренную задачу оптимизации можно

аналогично разделу 4 распространить на случай произвольных выпуклых ог-

раничений (5.92) или вогнутых определенного класса (подраздел 6.6), ис-

пользовав для этого полученные решения как итерационные. В общем случае

введение дополнительного критерия стоимости может существенно изменить

область допустимых решений М

xi opt

и множество оптимальных решений М

opt

Исходя из рассмотренного, можно сделать следующие выводы.

1. Задачу оптимизации систем можно н несложно распространить, поль-

зуясь разработанной методикой, на случаи более полного состава ТТТ, на-

пример, включающими указанные в подразделе 5.6 показатели качества.

2. На оптимальном решении, влияющем на сигнал, или сигнальную

функцию

( )

X∆ψ

(5.92), структуру и параметры системы и поисковых эле-

ментов, может существенно сказаться как состав ТТТ, так и численные зна-

чения хотя бы одного из показателей качества и ограничений.

3. Показатель скрытности N

скр

влияет на оптимальное решение следую-

щим образом: при малом

3nскр

tN ≤

показатель скрытности не влияет на оп-

тимум по t

при

nскр3n

tNt ≤≤

ограничение по скрытности становится более

жестким, infinum t

менее глубоким, а решение неоднозначное, при

скр1n

Nt ≤

ограничение по скрытности настолько жесткое, что критерий min

позволяет в качестве infinum брать точку на множестве, определяемом пе-

ресечением поверхности критерия t

и нижней грани ограничения по скрыт-

ности.

4. Уменьшение вероятности ложной тревоги F

лт

, как и уменьшение ве-

роятности правильного обнаружения Д, или отношения сигнал/шум q, при-

водит к сужению области допустимых решений, к увеличению оптимальных

значений времени поиска t

, что делает ограничение по скрытности менее

жесткими.

5. Изменение формы функции неопределенности, когда она сужается по

одному из параметров, приводит к смещению области оптимальных решений

по t

в сторону других параметров.

147

РАЗДЕЛ 6

МНОГОШКАЛЬНЫЕ И МНОГОЭТАПНЫЕ ИЗМЕРИТЕЛИ

6.1. Многошкальное устройство оценивания

параметров сигнала

Для случаев, когда требуется создать высокоточный, но экономичный и

оперативный измеритель параметра λ с широким априорным диапазоном, час-

то используется многошкальный измеритель, который может не уступать по

вектору названных показателей качества другим типам измерителей. Под мно-

гошкальным измерителем обычно понимается такой измеритель, у которого

точная шкала, содержащая точный дискриминательный измеритель с периоди-

ческой дискриминаторной характеристикой, дополняется грубыми с возможно

периодическими шкалами, разрешающими неоднозначность измерений на точ-

ной шкале. Обычно речь идет о фазовых измерителях задержки сигнала или

углов, хотя можно показать применимость многошкального метода и для изме-

рения частоты сигнала и других его параметров. Причиной высокой точности

фазовых измерений считают [4, 5, 16] значительную вторую производную от

сигнальной (например, автокорреляционной) функции по измеряемому пара-

метру λ. Однако из подраздела 2.3.7 видно, что высокая точность определяется

при заданном отношении сигнал/шум большой крутизной дискриминаторной

характеристики. Если использовать для фазовых измерений периодический

сигнал с достаточно крутыми фронтами, то можно достичь большой крутизны

дискриминаторной характеристики, однако при этом ширина спектра сигнала

будет большой. Это означает, что потребуется большая полоса пропускания

системы. Мощность шума при этом увеличится пропорционально полосе про-

пускания. Из этих соображений лучше работать с чисто гармоническим сигна-

лом. Причем, крутизну можно повышать увеличением частоты колебаний.

Действительно, если сигнал гармонический

S t S t

( ) cos= ω

то

′

t S t

( ) sinω ω

Платой за высокую точность фазовых измерений параметра сигнала λ при

большом априорном диапазоне является необходимость разрешения неодно-

значности измерений за счет введения дополнительных грубых шкал. В перио-

дическом сигнале в качестве дискриминаторной характеристики может быть

использована зависимость

S t( )

лишь в одном периоде. Если диапазон, напри-

мер, задержек больше периода, то требуется разрешать неоднозначность изме-

рений путем использования другого сигнала с меньшей частотой, или с боль-

шим периодом, однако и с меньшей точностью.

Возможность реализовать высокие точности измерений делают фазовые

измерения весьма популярными. Их приспосабливают для измерений многих

148

параметров сигнала. Эта возможность основана на следующей зависимости

полной фазы колебаний

Φ = − +ω τ ϕ( )t

от частоты

, задержки

,начальной фазы

. Измеряя полную фазу при из-

вестной частоте, мы оцениваем задержку, а при известной задержке оцениваем

частоту. Аналогично для электромагнитного поля

Φ =

2π

Измеряя фазу, или разность фаз, оцениваем разность хода волн при из-

вестной длине волны

В радиотехнике чаще всего отношение требуемого диапазона измерений к

требуемой погрешности измерений достаточно велико. Поэтому приходится

применять фазовые измерители со многими шкалами.

В настоящее время известен ряд трудов, посвященных многошкальным

измерителям. Среди них работы таких ученых, как А. Е. Башаринова, В. В.

Акиндинова, посвященные эффективности двухшкального измерителя, Н. В.

Собцова, посвященная синтезу оптимальных алгоритмов, работы М. М. Тенен-

баума, А. С. Созиева, С. Е. Фальковича [4, 3, 16, 17], посвященные исследова-

ниям точности двухшкальных измерителей и др. Однако исследуемые в этих

работах численные методы исследования моногошкальных систем не дают

возможности определить общие закономерности, присущие многошкальным

системам. Такие закономерности были получены, благодаря использованию

системного подхода. Имеем в виду влияние на облик системы показателей ка-

чества системы, и в частности, условий сопряжения апертуры дискриминатора

каждой шкалы с априорным диапазоном, величины априорного диапазона, до-

верия к оценке, стоимости измерителя и времени оптимизации. Полученные

результаты помогут более рационально и эффективно решить задачу с большей

степенью сложности, т.е. оптимизировать систему, описываемую большим

числом функциональных ограничений, полученных при формализации зависи-

мостей показателей качества от технических параметров.

В соответствии со сказанным рассмотрим задачу синтеза многошкального

измерителя запаздывания сигнала. Для того чтобы поставить задачу оптимиза-

ции, необходим широкий, но корректный системный анализ.

Сформулируем критерий качества многошкального измерителя запазды-

вания сигнала, используя в данной задаче следующие допущения:

- помеха представляет собой белый гауссов шум любого происхождения;

- измеритель оценивает параметр, мало меняющийся за время наблюде-

ния;

- сигнал отыскивается в классе гладких функций, что соответствует физи-

ческой картине;

- измеритель будет оптимизироваться с учетом следующих факторов: ап-

риорная дисперсия, коэффициенты доверия (доверительный интервал шкал),

рабочие частоты шкал, требуемая точность, время оценивания.

149

Если рассматривать вопрос об оптимизации высокоточного измерителя

запаздывания сигнала при ограничении на время оценивания, на стоимость и

интервал априорной неопределенности, который должен быть не меньшим

требуемого, то скорее всего, мы придем к выводу о том, что такой оптималь-

ный высокоточный измеритель запаздывания сигнала будет многошкальным, а

метод оценки - фазовым, если отсутствуют, разумеется, дополнительные тре-

бования к скрытности, сигнальной совместимости и пр.

6.2. Показатели точности многошкального

устройства

Стремление рассмотреть высокоточный измеритель основано на знании

того, что самой высокой потенциальной точностью измерения запаздывания

сигнала при равной энергетике обладают фазовые методы измерений. Этот

факт во многом известен [5] и, кроме того, будет доказан ниже при наличии

дополнительных критериев. Однако фазовые методы измерений имеют тот не-

достаток, что для раскрытия неоднозначности отсчетов требуют применения

нескольких шкал. Последнее существенно усложняет измеритель и в итоге ста-

новится неясным, какой измеритель является лучшим по точности измерений

при равных требованиях к ассигнованиям на систему, к коэффициенту доверия

и при равной априорной неопределенности. Ответы на этот вопрос можно по-

лучить, использовав синтез радиотехнических измерителей по названным кри-

териям, поскольку сравнивать целесообразно лишь оптимальные в указанном

смысле системы.

При рассмотрении показателя точности измерителя будем исходить из то-

го факта, что наилучшую точность может реализовать тот измеритель парамет-

ра λ, у которого наибольшее отношение сигнал/шум на выходе при прочих

равных данных. А наибольшее отношение сигнал/шум в канале обеспечивается

согласованной фильтрацией сигнала (корреляционным приемом, формирую-

щим на выходе канала сигнал, пропорциональный его функции автокорреля-

ции Ψ(λ)). Дискриминаторная характеристика U

∂

(λ) может быть реализована

как с применением схемы формирования функции автокорреляции Ψ(λ), так и

без нее. Естественно, что лучше ее применять, чтобы получить на выходе схе-

мы обработки сигнала наибольшее отношение сигнал/шум и наибольшую кру-

тизну дискриминаторной характеристики, а поэтому и наибольшую точность

измерений.

Для одноканального дискриминатора

( ) ( )λ ψ λ=

[ ]

( ) ( )

λ ψ λ

ψ λ ψ λ

′

≅

+ −

1 1

∆λ

для двухканального,

д2 1 2

2 2( ) ( / ) ( / )λ ψ λ ψ λ= + − −∆λ ∆λ

и соответствую-

щее значение

[ ]

д2

′

150

Для реальных радиоприемников напряжение U

Φвых

(t,λ) на выходе канала

или согласованного фильтра используется как характеристика дискриминатора,

т.е.

U t U S t g t t dt

вых д

λ λ λ( , ) ( ) ( , ) (

)= = −

∫

1 1 1

где g(t-t

) - импульсная характеристика согласованного или несогласованного

фильтра. Если g(t-t

)=g

S(t-t

), то для согласованного фильтра

U g S t S t t dt

д o

( ) (

, ) ( )λ λ= −

∫

1 1 1

Итак, дискриминатор может обеспечить высокую точность измерений при

заданном отношении сигнал/шум, которое может быть наибольшим при согла-

сованной фильтрации. Эта точность может достигаться, и в прецизионных из-

мерителях обычно достигается, ценой уменьшения апертуры дискриминатора

(смотрите соотношения (2.11), (2.12) и рис. 2.11, 2.12). Но в радиотехнических

измерительных системах диапазон измерений, соответствующий априорной

неопределенности измеряемого параметра, требуется большой. Разрешить про-

тиворечие между точностью и диапазоном измерений можно любым из опи-

санных в разделе 2 классификации методов: поисковым, многоканальным,

многошкальным, многоэтапным и комбинированным.

В данном разделе мы интересуемся многошкальным методом. Многош-

кальным измерителем назовем такой измеритель, у которого дискриминатор-

ная характеристика периодическая. Наиболее часто используется фазовый дис-

криминатор. Идея многошкального метода заключается в том, что вначале ис-

пользуется хотя и грубый дискриминаторный измеритель, зато перекрываю-

щий своей апертурой весь априорный диапазон. Точность такого измерителя

конечно будет низкой. Однако, после первого измерения диапазон неопреде-

ленности по измеряемому параметру существенно уменьшится. Если апертуру

первого дискриминатора сделать равной диапазону измерений, или довери-

тельному априорному интервалу (это у нас называлось сопряжением), то после

измерений доверительный интервал с тем же доверием к оценке уменьшится в

число раз, равное отношению сигнал/шум (2.13, 2.14). Напомним, что сопряже-

ние необходимо для того, чтобы не было неоднозначности измерений, когда

диапазон измерений больше апертуры дискриминатора, и чтобы получить наи-

большую крутизну дискриминаторной характеристики, или наибольшую точ-

ность, когда диапазон измерений меньше апертуры дискриминатора (2.16). По-

следовательно применяем второй дискриминатор, у которого апертура соответ-

ствует доверительному интервалу, полученному в результате измерений пер-

вым дискриминатором. И так далее с требуемой точностью. Число таких изме-

рений и дискриминаторов (шкал) быстро сокращается с ростом отношения

сигнал/шум. Поскольку сразу использовать точную шкалу нельзя ввиду много-

значности измерений, то фактически все предыдущие шкалы играют роль из-

мерителя, разрешающего неоднозначность измерений. Такой измеритель мо-