Алешин Г.В., Богданов Ю.А. Эффективность сложных радио-технических систем

Подождите немного. Документ загружается.

А другое его значительное преимущество перед известными методами — в том, что про-

грамма оптимизации может быть составлена заранее, до того, как станет известной форма зави-

симости

( )

C X

Линеаризация

( )

C X

делает математическое программирование сепарабельным, что позво-

ляет отыскать аналитические решения по блокам (по группам) параметров.

В частности,

{ } { }

i i

const

min min

∏

′

∏













, (3.1.6)

при

′

∑

≤

C X C

i i

э0

где

n C

i opt

′

, (3.1.7)

C C C X

э n i i

1 1 0 0

= +

′

∑

∆

∆C C C

n i

1 1 0

= −

∑

{ } { }

( )

j j

min min

2 2

∑

′

∑

, (3.1.8)

при

′

∑

≥

C X C

j j

э0

где

( )

C C

э j

j opt

′

∑

2 0

, (3.1.9)

C C X C

э j j

n2 0 0

′

∑

−

∆

∆C C C

n j

2 2 0

= −

∑

Затем отыскивается

( )

∆

C B

Д C

























−













min min

при

∆ ∆ ∆C C C

n n1 2

+ ≤

где

A const n C

′

∏

B C X

i i

′

∑

0 0

( )

ε =

′

∑

Д C X

j j

′

∑

0 0

Оптимальное решение

∆C

n2 opt

отыскивается методом Ньютона-Рафсона из уравнения

( )

B C C

Д C

1 1

+ −

= −

∆ ∆

∆

opt

Отсюда

[ ]

∆

∆ ∆

C B C A

A n C B C

n k

2 1

1 2

1 1

( )

= −

+ −

+ + + −

−

. (3.1.10)

Для

( )∆ ∆C B C

+ >>

( ) ( )∆C B

A n+ >> +

1 1ε

∆

C Д

C B

1 1

opt

≈ −

( )

. (3.1.11)

Тогда

{ }

n n

C B Д

C B

min

( ) ( )

( )

σ ε

2 1 1

≅

+ −













∆ ∆

. (3.1.12)

Оптимальное решение определяется из формул (3.1.11), (3.1.9) и (3.1.7). Очевидно, что при

некоторых больших ассигнованиях суммарная дисперсия погрешности измерений уменьшается

незначительно. Поэтому, исходя из принципа достаточности, существует оптимальная аппара-

турная погрешность и оптимальные ассигнования на систему.

В такой задаче можно использовать все технические параметры реальных систем, для кото-

рых известна статистика по стоимости. Если в системе есть канал синхронизации, в котором не

оценивается дальность и который поэтому можно считать служебным, то дисперсия погрешно-

сти синхронизации также служит техническим параметром. А если с помощью канала синхрони-

зации оценивается дальность, то система становится совмещенной и процедура оптимизации ее

усложняется.

Следует помнить, что оптимум определяется для самого худшего случая: для измерений на

максимальной дальности или для случая наибольших флуктуационных помех.

3.2. Оптимальный выбор структур каналов измерительных радиотехнических систем

Инфраструктура системы становится известной обычно в результате выбора навигационного

принципа измерений при известном ее назначении. Поэтому речь идет о выборе оптимальной

структуры измерительного канала. Структура измерителя определяется методом оценивания

параметра сигнала.

Напомним, что методы оценивания параметров сигнала могут быть [45]:

1) дискриминаторными;

2) поисковыми, или панорамными;

3) многоканальными;

4) многоэтапными;

5) многошкальными;

6) комбинированными.

Структуры, реализующие указанные методы, относятся к, так называемым, первичным из-

мерителям, которые производят единичное измерение за время наблюдения, отсчет и регистра-

цию результата измерения. Вторичные измерители производят обработку массива измерений с

целью повышения точности либо путем физической фильтрации процесса параметра, либо с

помощью «цифровой фильтрации», т. е. последовательной (в темпе времени) обработки резуль-

татов измерений или одновременной по мере их накопления. Нас будут интересовать качествен-

ные, т. е. самые точные и самые широкодиапазонные, а, значит, самые сложные, измерительные

системы. Простые системы будут фактически частным случаем. Деление измерителей на пер-

вичный и вторичный является в известной степени условным. Возможно исполнение этих функ-

ций в одном измерителе. Получение результатов измерений в цифровой форме имеет ряд пре-

имуществ перед аналоговой формой. Это удобство работы с универсальными ЭВМ, удобство

обработки результатов по гибкой программе, сужение полосы пропускания до значений, кото-

рые нереализуемы аналоговым способом и другие.

Недостатками цифровой обработки являются сложность и дороговизна цифровой обработки,

которые должны удовлетворять также требованиям по широкополосности, по быстродействию,

по надежности функционирования, по помехозащищенности и другие. Эйфория от достоинств

цифровой обработки стимулировала предложения по оцифровке сигнала сразу после антенны.

Такие предложения неправомерны, поскольку:

1) растет коэффициент шума радиоприемника и соответственно падает его чувствитель-

ность,

2) еще не существует такого аналого-цифрового преобразователя, который бы работал со

столь малым сигналом,

3) не будет никакой избирательности системы по частоте и другим параметрам селекции,

4) создать аналого-цифровой преобразователь с чрезвычайно широкой полосой пропускания

и большим динамическим диапазоном проблематично,

5) не будет хорошей помехоустойчивости.

По-видимому, для сохранения требуемых качеств измерительные радиосистемы всегда бу-

дут содержать кроме антенны, как минимум, преселектор и преобразователь частоты.

Выбирая оптимальную структуру измерителя, или метод оценивания параметра сигнала,

следует сразу оговорить, что мы понимаем под термином «оптимальную». Как и ранее, ввиду

того, что показано преимущество условного критерия качества, оптимальность будет означать,

что именно по этому критерию. Под эффективностью будем понимать величину приращения

условного критерия качества рассматриваемой системы по отношению к известной системе.

Состав показателей качества, их отбор производится обычно в соответствии с назначением сис-

темы и технических требований к ней. Очевидно, что различный состав основных показателей

качества делает системы несравнимыми.

Поэтому выбор оптимальной структуры измерителя производится по условному критерию

качества при том же составе показателей качества, которые использовались для параметриче-

ского синтеза. Только это выбор дискретных структур. На основании изложенного можно ука-

зать оптимальные методы для малого состава показателей качества. Например, если требуется

только высокая точность, то все методы оценивания пригодны, кроме поискового и многока-

нального для очень высоких точностей, для которых нереализуема такая апертура дискримина-

тора. Если, кроме того, требуется широкий диапазон измерений, то дискриминаторный метод

непригоден. Если, кроме того, требуется малое время наблюдения, то поисковый метод исклю-

чается, лучший для этой цели многоканальный метод. Если, кроме того, требуется малая стои-

мость, то многоэтапный (или многошкальный) метод может оказаться лучшим. Если интересует

малая стоимость, а не время наблюдения при заданных

−2

λa

−2

, то поисковый метод лучше.

Если увеличить доверие к оценке, то требуемое число шкал, стоимость и время наблюдения рас-

тут у всех методов измерений.

А вот, если потребовать лучшие значения всех показателей, то какой метод станет лучшим,

неясно. Мы сравниваем методы по одному показателю качества при равных остальных. Поэтому

неясно, какой метод станет лучше, если, например, сравнивать по времени измерений при про-

чих равных значениях показателей качества. При равной стоимости поисковый метод может

оказаться лучше многоканального, если стоимость, затрачиваемую на каналы, кроме одного,

затратить, например, на увеличение мощности передатчика, КНД антенны и т. п.

Поскольку дискриминаторный и многошкальный методы являются при оценке эффективно-

сти частным случаем многоэтапного метода, число вариантов для попарного сравнения по ус-

ловному критерию качества можно существенно сократить.

Будем сравнивать системы по оперативности (по времени измерений

) при прочих равных

данных.

Тогда получим

q N

P X

1 01

1 1

∏

q N

P X

2 02

2 2

∏

(3.2.1)

q N

P X

3 1

03 1

3 1 2

( )

∏

q N

P X

3 2

03 2

3 2 3

( )

∏

где индекс 1 означает поисковый метод оценивания, 2 — многоканальный, 3(1) — много

шкальный (параллельный ), 3(2) многоэтапный (последовательный),

N N N

01 02 03

= =

— спектральная плотность шума,

X X

1 2

∏

— произведение одних и тех же остальных параметров системы,

q q q

1 2 3

= =

— мощность передатчика.

В выражениях для времени наблюдения

нет уравнения связи для ассигнований С на сис-

тему. Если можем варьировать мощностью передатчика

, то получим

( ) ( )

( )

C C P C X C C C

C C P C X n C C

C C P C X n

C C

C C P C X C C C

P X i

X i

k k

P X i

э э

P X i

1 1 1 01

2 2 2 02

3 1 3 3 1 03 1

3 2

3 3 2 03 2

= +

∑

+ + +

= +

∑

+ +

= +

∑

+ +

= +

∑

+ + +

упр 1

упр 3(1)

( ) ( ) (

)

( ) ( ) ( )

, (3.2.2)

где

k, э

— стоимость канала или этапа,

— стоимость остальной части системы,

упр

— стоимость схемы управления перестройкой,

k, э

— число каналов, этапов,

( )

C P

iP i

— стоимость передатчика.

В общем случае варьировать нужно всеми техническими параметрами, сохраняя их опти-

мальные соотношения, от которых зависит время наблюдения. Если варьируется один самый

дорогой элемент, например, передатчик, то принятие решения о структуре можно упростить.

Зная зависимость

( )

C P

i i

, для систем связи

C K K P

= +

1 2

, и разрешив выражения (3.2.2) от-

носительно

, подставляем их в формулы (3.2.1). Теперь время наблюдения параметра зависит

и от стоимости.

Сравнение времени наблюдения измерителей будем производить попарно, вычисляя отно-

шение

, которое уже не зависит от остальных параметров систем, т. к.

q N X

i i i

∏

для них

одинаковы.

Тогда

nЭ

13 1

3 1

13 2

3 2

1 2

23 1

3 1

23 2

3 2

1 2

= ≈

−













= ≈

−













= ≈

−

= ≈

−













= ≈

−

( )

−













nЭ

(3.2.3)

где

≅

q q

Э шк

= +1

шк

— отношение сигнал / шум в шкале,

1 01

−

∑

−

C C C

При этом предполагалось, что

C C

упр

. Это условие всегда выполняется. Структура i-го

измерителя, которая на основе векторного сравнения соответствует наименьшему времени на-

блюдения

, будет оптимальной по условному критерию качества.

3.3. Выбор оптимального сигнала измерительной радиотехнической системы

Новый подход к измерениям позволяет по-новому увидеть проблему синтеза оптимального

измерительного сигнала. Во-первых, всегда следует иметь ввиду, что понимается под словом

«оптимальный». Если от системы требуется измерить параметр

с самой высокой достижимой

точностью, не указывая, в каком диапазоне это сделать, то самым простым измерителем при

этом будет дискриминаторный измеритель с минимально достижимой апертурой

2∆λ

∂

и с мак-

симально возможным отношением сигнал / шум q. Тогда будет обеспечена максимальная кру-

тизна дискриминатора и максимальная точность измерений. Однако, при этом точность покупа-

ется за счет ухудшения другого показателя — априорного диапазона измеряемого параметра.

Тем не менее, в прецизионных системах на это идут. Рассмотрим теперь, какой должен быть

оптимальный сигнал для этих двух требований — по точности и по априорному диапазону. При

малом априорном диапазоне можно также увеличивать отношение сигнал / шум за счет узкой

полосы пропускания системы, для любого измеряемого параметра. Это означает, что оптималь-

ный сигнал должен быть гармоническим. Фазометрические измерители задержки, угловых ко-

ординат цели и даже доплеровской частоты работают обычно с гармоническим сигналом. Их

дискриминаторные характеристики также гармонические. Поэтому оптимальны цифровые фа-

зометры, где наибольшая крутизна достигается при переходе их через 0. Оптимальным следует

считать также следящий измеритель частоты, поскольку он работает именно на этом самом кру-

том участке дискриминаторной характеристики и поскольку реализуется возможность сужения

полосы пропускания. Отсчет частоты целесообразно производить от управляемого гетеродина

цифровым частотомером, в котором также используется самый крутой участок синусоиды в ре-

зультате ее предельного ограничения. Если требуется расширять априорный диапазон измере-

ний задержки, то оптимальный сигнал может быть гармоническим, или узкополосным, если оп-

тимальными измерителями станут многоканальный и поисковый измеритель частоты, или изме-

ритель может стать полигармоническим для многоэтапных или многошкальных измерителей.

Значения оптимальных частот шкал для фазометрических измерителей представляют собой гео-

метрическую прогрессию. Они могут представлять собой частоты модуляции или их линейные

комбинации. Сигнал может быть последовательным, типа «мелодия» и параллельным типа «ак-

корд». Поскольку ряд гармоник может оказаться в одной полосе частот, ширину спектра сигнала

целесообразно выбирать такой же. Ряд гармоник многошкального измерителя можно получить

умножением частоты модуляции или какой-либо достаточно мощной частоты спектра. Степень

свободы в выборе сигнала позволяет некоторым образом удовлетворить и другим требованиям к

сигналу.

Поскольку частоты шкал могут оказаться в одной полосе пропускания системы, то при не-

высоких требованиях к точности измерений могут быть использованы и методы слежения за

задержкой фронтов сигнала.

Для фазовых измерений угловых координат справедливы выводы об измерителях задержки,

поскольку фактически фазовым методом измеряется задержка поля (или его фазового фронта)

на другом конце базы.

Для измерений частоты оптимальным сигналом является лишь одна гармоника. А оптималь-

ный измеритель (его структура) может быть получен предложенным методом. Однако послед-

нюю шкалу оптимально реализовать как следящий узкополосный дискриминатор (ФАПЧ), если

динамическая ошибка не велика, с отсчетом частоты цифровым методом от управляемого гете-

родина.

4. Оптимизация совмещенных радиотехнических систем

Аппаратурно совмещенными называют такие системы, которые одной и той же аппарату-

рой, или частью ее, обрабатывают общий сигнал, позволяющий выполнять одновременно не-

сколько различных функций или назначений системы. Кроме аппаратурного используют также

сигнальное совмещение. Сигнальным называется такое его совмещение, которое позволяет

практически одновременно принимать и обрабатывать сигналы, предназначенные для выполне-

ния различных функций системы. Совмещенная аппаратурно и (или) сигнально система может

практически одновременно производить обнаружение сигнала, измерение одного или несколь-

ких параметров цели, передачу ее бортовой (связной) информации и телеметрических данных.

Ввиду дороговизны аппаратуры радиотехнического диапазона, особенно антенн, передатчиков,

фидеров, пре селекторов, преобразователей и радио усилителей, а также ввиду удобства исполь-

зования одного электромагнитного контакта с целью, совмещенные системы достаточно эффек-

тивны. Аппаратурное совмещение особых неудобств не представляет ввиду достаточной широ-

кополосности аппаратуры радиотехнического диапазона. Сигнальное совмещение значительно

сложней. Для совмещения или разделения сигналов используются следующие параметры селек-

ции: частота, время, структура сигнала или составляющие его спектра или реже параметры по-

ляризации. Разделенные части общего сигнала поступают в соответствующие каналы системы

для обработки (рис.4.1.1). Сечение разделения сигнала по каналам обычно достаточно низкочас-

тотно. При этом разделение не обязательно должно быть в одном сечении системы, хотя это

весьма удобно.

Проблема разделения общего сигнала по каналам заключается в том, что на каждый канал

воздействует, так называемая, взаимная помеха, т. е. сигналы, предназначенные для других ка-

налов.

Проблема оптимизации совмещенных систем состояла в том, что было неясно, как учесть

аппаратурное и сигнальное совмещение при формализации задач, как сформулировать задачу,

как учесть основные показатели качества и т. п. Ответ на ряд таких вопросов уже получен в пре-

дыдущем разделе.

4.1. Постановка и решение задачи параметрического синтеза совмещенных РТС

Существующие и перспективные РТС обычно строятся таким образом, что большинство ка-

налов обработки сигналов, после высокочастотной части системы можно считать независимыми.

Исключение могут составлять совмещенные РТС, использующие сложные сигналы. Однако при

малых требуемых ошибках синхронизации и отслеживания частоты системой ФАПЧ и каналы

обработки информации также можно считать независимыми. При постановке задачи использу-

ются предположения о том, что система высококачественная и применяет последовательный

составной сигнал. Это предположение является более общим, поскольку всегда возможно упро-

щение задачи для случаев простых сигналов. Наличие в структуре полного или частичного со-

става блоков определяется лишь в результате параметрического синтеза, который дает оконча-

тельный ответ о целесообразности применения каждого блока и о его параметрах. В этом отно-

шении параметрический синтез является тесно связанным со структурным. Использование в

РТС последовательных составных сигналов предполагает самую общую структуру, включаю-

щую устройства формирования и обработки сложных сигналов. При этом характеристики рас-

строек, не идеальностей и возмущений в этих устройствах формально так же входят в выраже-

ния для дисперсией ошибок, как и в системах с простыми сигналами. Поэтому формализованная

задача может быть применима для широкого класса сигналов. Взаимосвязь параметрического

синтеза РТС с синтезом сигналов проявляется на этапе расчетов оптимальных технических па-

раметров по общим формулам, в которые входят также зависимости качественного показателя

от сигнальных параметров.

Совмещенная РТС, имеющая укрупненную структуру вида рис. 4.1.1, обычно имеет один

основной, СВЧ радиоканал, в котором транслируется обычно один совмещенный радиосигнал,

несущий различную информацию для всех каналов обработки. Возможны и вспомогательные

радиоканалы, которые также являются общими для информации различного назначения. Поэто-

му вид структуры и связи качественных показателей существенно не изменятся.

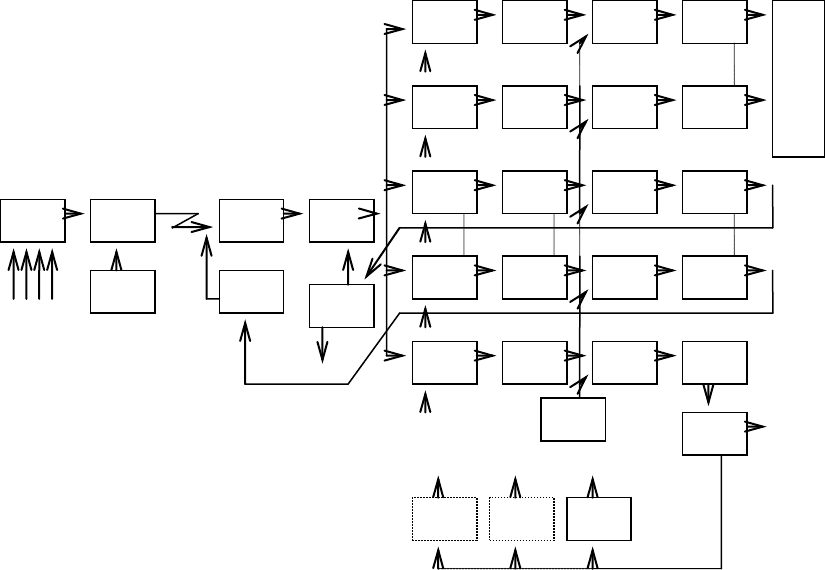
На рис. 4.1.1 представлена типовая укрупненная структура приемной части оптимизируемой

системы одной стороны радиолинии, использующей корреляционный метод приема последова-

тельных составных сигналов. Можно показать также, что приведенная далее методика парамет-

рического синтеза справедлива принципиально для любой структуры с независимыми или слабо

зависимыми каналами обработки информации. На рис. 4.1.1 приняты следующие обозначения:

1 — модулятор передатчика для передачи последовательных составных сигналов;

2 — передатчик;

3 — передающая антенна;

4 — приемная антенна;

5 — усилитель высокой частоты;

6 — смеситель;

7 7

, ,

— пере множители n каналов;

8 8

, ,

— узкополосные усилители промежуточной частоты;

9 9

, ,

— фазовые детекторы;

10 10

, ,

— фильтры нижних частот;

11 — генератор тактовых импульсов;

12 — перестраиваемый гетеродин;

13 13

, ,

— генераторы опорных последовательностей;

14 и 15 — задающие генераторы 1 и 2;

16 — автоматическая система наведения по углам;

17 — сравнивающее устройство, блок принятия решений.

На схеме не указаны блоки поиска сигнала по пространству, частоте и задержке, поскольку

критерий поиска целесообразно включать в задачу на последующем этапе.

Система оптимизируется таким образом, чтобы найти оптимальное распределение ассигно-

ваний по блокам системы, или оптимальные параметры с точки зрения минимума ассигнований

на всю систему при ограничениях на качественные показатели системы и по условиям физиче-

ской реализуемости параметров. Технические параметры количественно описывают некоторое

Гcm

СМ

УВЧ

ГТИ

АСМ

ЗГ

ПРД

МОД

ФНЧ

ФД

УПЧ

•

ФНЧ

ФД

УПЧ

ФНЧ

ФД

УПЧ

10p

ФНЧ

ФД

УПЧ

∂

10m

ФНЧ

ФД

УПЧ

ГПСП

Ср.

Рис 4.1.

качество соответствующих систем блоков. Поэтому найденные в результате решения параметры

должны быть исходными данными для детальной разработки принципиальной схемы и конст-

рукции соответствующих блоков из унифицированного ряда при проектировании. Назовем в

качестве примера некоторые основные технические параметры системы, которые могут описы-

вать качество блоков. Антенны могут описываться коэффициентами направленного и полезного

действия, коэффициентами использования площади антенны, фидерные устройства — коэффи-

циентами затухания, коэффициентами бегущей волны, усилители высокой частоты — шириной

полосы пропускания, коэффициентами усиления и коэффициентом шума, смесители — коэффи-

циентом преобразования и коэффициентом шума и т. д. Поэтому для большинства измеритель-

ных каналов с учетом указанных факторов

X X

∏

∑

, (4.1.1)

где

— дисперсия ошибок за счет незнания условий распространения радиоволн,

— среднеквадратическая ошибка за счет нестабильности эталонов и других факторов.

Покажем, что такой критерий, как вероятность безошибочной передачи дискретной инфор-

мации, передаваемой в РТС, также можно представить в виде (4.1.1). В системе возможно ис-

пользование ансамбля кодов с алфавитом m. Будем предполагать, и обычно это всегда выполня-

ется, что коды, применяемые в системе практически ортогональны. Если сигналы практически

ортогональны, то можно использовать следующую формулу для средней вероятности ошибки

передачи информации

p m

ош ср

= − − −













14exp ,

, (4.1.2)

где q — соотношение сигнал / шум на выходе приемника.

Считая среднюю вероятность ошибки передачи информации меньше допустимой, имеем ог-

раничение на отношение сигнал / шум

1 1

2 8

≤

−

ln ,

ош доп

p доп

. (4.1.3)

Таким образом, отношение сигнал/шум можно записать в факторизованном виде, в виде

произведения функций технических параметров, как и показатель (4.1.1).

Аналогичные соотношения можно получить для любой схемы обработки сигнала.

Даже если статистика стоимости задана в виде дискретного, пусть даже унифицированного,

ГОСТированного ряда элементов, при большом числе оптимизируемых параметров не обойтись

без интерполяции и функционального представления зависимости стоимость—параметр. Такой

подход позволит избежать сложности, неразрешимости стохастического программирования и

позволит получить общее решение в довольно обозримом виде. Поэтому представим многомер-

ную среднеквадратическую регрессию стоимости на параметры в самом общем виде

( ) ( )

C X X C X C X X C X X X

N k k

l l l

t t t t

1 2 1 2 3

, , , , , =

∑

, (4.1.4)

где k — параметр суммирования стоимости блоков, описываемых одним техническим пара-

метром,

l — двумя,

t — тремя техническими параметрами и т. д.

Пусть среди всех параметров группы i имеется k, а среди группы j имеется l таких, которые

описывают совмещенные блоки (например, блоки 1—6 на рис. 4.1.1). При этом предполагается

также сигнальное совмещение, либо отсутствие его, но последовательное во времени использо-

вание каналов. На формализацию задачи это обстоятельство не сказывается. Поскольку k пара-

метров группы i являются общими в произведении

∏

, обозначим их произведение большой

буквой

, и назовем его параметром совмещения группы i.

∏













−

. (4.1.5)

Поскольку l параметров группы j также являются общими, их сумму обозначим буквой

назовем параметром совмещения группы j

X L

∑

≤

. (4.1.6)

Учитывая обозначения (4.1.5, 4.1.6), ограничения на параметры

, можно записать с

разделенными переменными, что позволяет воспользоваться методом решения, изложенным в

разделе 3.

F B B C X C X

p p opi pi

opj pj

p p

= + +

′

∑

−

′

∑













∑













= ==

min

1 2

1 11

1 2

[ ] [ ]

X Д L

i n n

n l

p j

p p p

p k

p1 пред

pj пред

0 X

−

∏

≤ ≤ ≤

∑

≤ −

≤ <<

∀ ∈ ∀ ∈











1 2

1 1

, , ,

(4.1.6)

X K

X L

∏

≤

∑

≤











для совмещенной части параметров.

Проделав первые шаги оптимизации (3.1.6—3.1.12) и перенумеровав слагаемые, получим

F B B Q K Q Д L Q K Q L

p p

n k

n l p k

= + + − −













+ −

∑

























−

1 2

min

, (4.1.7)

где

( )

Q n k

Д C

n k p

opi

n k

−

= −

′

∏

p пред

Q k C

k oi

′

∏

Q C

n l opj

n l

−

′

∑

Q C

l oj

′

∑

Предположим, что число оптимизируемых параметров

в каналах одинаково, т. е.

n n n n

p11 21 1

= = =

. Тогда

F B B K Q K Q Q Д L Q L

p p

n k

k n l p

p p

= + +

∑

+ − −

∑

−

























−

1 2

min

. (4.1.8)

Минимум по

легко находится из выражения (4.1.8)

n k

i opt

n k

n k k

−

∑













−

( )

. (4.1.9)

При отыскании

j opt

следует учесть то обстоятельство, что обычно на практике

L Д

поскольку совмещенный блок как эталон для измерений представляет собой задающий генера-

тор, или стандарт частоты и т. п.

Таким образом

n l

j opt

≅

∑













−

. (4.1.10)

Точнее

j opt

можно определить из кубического уравнения

( )

Д Д

n l

p p

n l

p p

2 2

−

∑

− =

пользуясь решением Кардано. Минимальные ассигнования на совмещенную систему опре-

деляются из (4.1.8) с учетом (4.1.9, 4.1.10)

( )

F B B

Q Q

Q Д

Q Q

p p

n l

n l p

n l

l l

p l

= + +

∑













−













−

∑ ∑













− +

∑

−

1 2

2 2

. (4.1.11)

Оптимальные технические параметры находятся в следующем порядке. Сначала определя-

ются оптимальные параметры совмещения

, затем параметры совмещенной части сис-

темы по формулам (3.1.10, 3.1.9, 3.1.7). Определив отношение

, по тем же формулам легко

определить остальные технические параметры группы i, а, зная разность

Д L

p j2

−

, можно опре-

делить остальное технические параметры группы j. По формулам (4.1.8, 4.1.9, 4.1.10) определя-

ются также оптимальные ассигнования на блоки системы.

Далее можно определить оптимум F для p каналов, вводя ограничение

Д Д Д

p p p1 2

+ ≤

. Оче-

редными шагами несложно отыскать оптимум F также для всех ранее не оптимизируемых пара-

метров, заложенных в коэффициенты

4.2. Оптимизация параметров совмещения РТС

Как видно их приведенных выражений, параметрический синтез совмещенных систем воз-

можен для произвольного числа независимых измеряемых параметров, каналов и ограничений.

Среднее геометрическое угловых коэффициентов линий регрессии стоимости на параметры со-

вмещенных блоков обозначим

′

ос

, а не совмещенных блоков —

′

о нр

′

∏

C C

ос oi

′

∏

−

C C

о н opi

n k

Тогда нетрудно из (4.1.8) заметить, что

[ ]

F n C C

oc opa p

′

+ −

′

∑













−

exp ln ( )ln

( )

α α ε

, (4.2.1)

где

′

opa

— среднеарифметическое значение

′

о нр

по всем p каналам,

α =

п ед о н о а

о а

С С

= −

′

−

′













р р

р1

При увеличении

, или числа параметров совмещенных блоков (k), ассигнования

, как и

следовало ожидать, уменьшаются, поскольку

и экспоненциальный множитель также