Алешин Г.В., Богданов Ю.А. Эффективность сложных радио-технических систем

Подождите немного. Документ загружается.

101

6. Оптимизация лазерной системы передачи информации

6.1. Особенности задачи оптимизации лазерных линий передачи информации

Рассмотрение задачи оптимизации лазерной линии передачи информации не является слу-

чайным. Лазерные системы ввиду своих неоспоримых достоинств - широкой полосы пропуска-

ния системы, большой концентрации энергии в телесном угле и других - при соответствующих

условиях применения: на заатмосферных объектах, высокогорных пунктах и т. д., могут в пер-

спективе стать достойным конкурентом совмещенным радиотехническим системам. Кроме того,

задача является более общей, чем рассмотренные ранее, поскольку система оптимизируется по

трем критериям качества: по стоимости при ограничениях на время поиска и на вероятность

безошибочной передачи информации. Тем более, что проблема поиска присуща также РТС, об-

ладающим антеннами высокой направленности. Разумеется, природа оптического диапазона

сказалась и на форме оптимального решения, т. к. вероятность ошибки передачи информации

имеет другую зависимость от сигнала и шума, обусловленную квантовой природой света. Одна-

ко, принципиально задача оптимизации радиотехнических систем выглядит так же при тех же

критериях.

Итак, взвесим достоинства и недостатки оптических систем и разберемся в существе про-

блемы. Можно отметить следующие достоинства оптических систем:

— большая полоса частот и соответственно большие возможности передачи большого объ-

ема информации с большой скоростью;

— возможность скрытной по углам передачи информации в чрезвычайно узком телесном

угле и большая помехоустойчивость;

— возможность уменьшения габаритов приемо-передающих устройств;

— высокая концентрация энергии в узком телесном угле;

— возможность увеличения дальности линий передачи информации;

— высокая стабильность колебаний;

— простота обработки пространственно-временных сигналов.

Эти достоинства оптических линий передачи информации делают их весьма эффективными

и перспективными для передачи информации на борт объекта и обмен информацией между сис-

темами объектов. Однако при всем этом имеют место серьезные проблемы и слабые места опти-

ческой связи, связанные, например, с прохождением сигнала через атмосферу, с поиском сигна-

ла по углам особенно для подвижных объектов, с реализацией больших полос пропускания мо-

дуляторов и др. элементов систем.

В настоящее время можно считать наиболее перспективным применение лазерных систем

для стыковки КА, космической связи, измерений параметров движения КА, обмен информацией

между системами объектов, прежде всего синхронными спутниками и др. Сравнительный анализ

сверхширокополосности оптических и СВЧ ретрансляционных линий [9, 10, 7] для передачи

информации между спутниками показал, что для оптических линий требуется меньшее на поря-

док значение потребляемой мощности передатчика, чем для наилучшей СВЧ-системы (частота

10 гГц). Следует иметь также ввиду, что и стоимость разработки оптических систем связи с по-

лосой, превышающей 400 МГц может быть меньше стоимости СВЧ систем, поскольку их эле-

менты, рассчитанные на названные значения полосы частот находятся почти в одинаковой ста-

дии развития. В случае же связи летательного аппарата с наземными пунктами или между под-

вижными объектами оптические линии передачи информации можно использовать в комплексе

с радиотехническими.

В настоящее время для построения различных оптических линий передачи информации

обычно используют лишь пути непрерывного усовершенствования их элементов и принципов их

работы. Такой путь несомненно правильный и необходимый, определяющий темпы и уровень

развития техники. Однако это не единственный путь усовершенствования систем и, в частности,

линий передачи информации. Возможен также путь усовершенствования систем за счет опти-

мального распределения усилий между элементами системы, называемый также параметриче-

ским синтезом.

Предположим, что при создании оптической линии передачи информации используются,

например, при заданных весах, габаритах и т. д. все предельно достижимые параметры (наи-

меньшая ошибка углового сопровождения, наибольшая мощность излучения, наибольшая поло-

са пропускания модулятора и приемника, наименьший уровень собственных и фоновых шумов и

т. д.). Такая линия передачи информации была бы исключительно дорога и практически непри-

емлема, т. к. каждый ее блок представлял бы собой последнее достижение науки и техники. По-

102

строение такой линии передачи информации очевидно нецелесообразно, поскольку качествен-

ные показатели и параметры такой линии будут лишь незначительно лучше применяемой при

существенном росте стоимости всей линии. А, ведь, если даже на систему выделены сколь угод-

но значительные ассигнования, все равно наилучшие качественные показатели будет иметь сис-

тема с оптимальными параметрами. Поэтому параметрический синтез систем актуален всегда, в

том числе, для мало серийных и дорогостоящих систем. Подобная задача оптимизации оптиче-

ской линии по критерию сигнал / шум при ограничении по стоимости решалась в работе [9, 10,

7]. При этом определяются лишь четыре оптимальных параметра системы: диаметр передающей

антенны, диаметр приемной антенны, мощность передатчика и поле зрения приемника. В труде

[10] минимизируется полная стоимость указанной части системы при сохранении заданного от-

ношения сигнал / шум как функции качества методом множителей Лагранжа, который не позво-

ляет получить, однако, решение в аналитическом виде, пригодном для целого класса случаев.

Задача решается на ЭВМ в численном виде. Однако, реальные оптические системы обычно яв-

ляются принципиально многопараметрическими системами, т. к. одна и та же система осущест-

вляет, по меньшей мере, поиск сигнала и взаимное слежение по направлению, а также прием и

передачу информации. Поэтому наряду с ограничениями, накладываемыми на отношение сигнал

/ шум (q) на выходе оконечного устройства, имеют место ограничения на время вхождения в

связь

и точность слежения. Наличие этих ограничений не учитывается в работе [10], но учи-

тывается в данном разделе при формализации задачи.

Решение задачи оптимизации лазерной системы передачи информации между подвижными

объектами при учете указанных ограничительных условий затрудняется в значительной мере из-

за сложности зависимостей, описывающих вероятности обнаружения оптического сигнала на

фоне шумов, что приводит к усложнению либо функций качества системы, либо ограничений.

В данном разделе формализована задача оптимизации системы лазерной связи между под-

вижными объектами в виде задачи вырожденного динамического программирования по крите-

рию минимума стоимости при ограничениях на время поиска связи и на соотношение сигнал /

шум в канале передачи информации.

6.2. Вхождение в связь приемо-передатчика лазерной системы

Оптимальное распределение средств, отпускаемых на построение системы лазерной связи, и

оптимальные параметры системы зависят от ее структуры, выбор которой является также зада-

чей оптимизации. В данном случае мы будем полагать эту структуру известной и типовой, опре-

деляемой имеющимся опытом проектирования таких систем и известными принципами их

функционирования.

При выборе окончательного варианта структурной схемы необходимо отметить, что харак-

терной особенностью лазерной системы передачи информации между подвижными объектами

является значительная величина угловых конусов, в которых происходит поиск объектов, что

связано, как правило, с большой начальной неопределенностью положения подвижных приемо-

передатчиков и с высокой точностью ориентации «антенн» лазерных приемо-передатчиков. В

ряде случаев величина этого конуса может превышать 10°. С другой стороны, обеспечение зна-

чительного превышения сигнала над шумом в канале приема и передачи информации, сообра-

жения скрытности и точности измерения углов требуют концентрации энергии в узких пучках с

расходимостью, составляющей несколько угловых секунд [10]. Расчеты, произведенные по дан-

ным работы [9], показывают, что время взаимного нацеливания лучей приемо-передатчиков при

таких условиях может достигать нескольких десятков минут. Расширение луча на период поиска

более чем в 100 раз является, с одной стороны, сложной технической задачей, а, с другой сторо-

ны, обеспечение приемлемой вероятности обнаружения сигнала при поиске требует значитель-

ной мощности передатчика. В настоящее время созданы мощные оптические квантовые генера-

торы, которые зачастую мало приспособлены для длительной передачи информации (требуют

для работы значительной энергии накачки и охлаждения). Однако они вполне могут быть ис-

пользованы на этапе вхождения в связь с целью уменьшения времени поиска связи

. В силу

сказанного, можно применить типовую процедуру поиска связи с использованием маяка.

При необходимости вхождения в связь подвижного объекта А с неподвижным объектом В

на объекте А включается маяк. Расходимость маяка устанавливается равной угловому конусу

неопределенности. Объект В осуществляет грубый поиск, например, с помощью фотоприемни-

ка, мозаичной структуры, расположенного в фокальной плоскости объектива телескопа. Этот

способ в настоящее время считается наиболее целесообразным [9]. Пусть приемник грубого об-

103

наружения (мозаичный приемник) имеет поле зрения в пределах угловой неопределенности объ-

екта А.

Вторым этапом является этап поиска сигнала маяка фотоприемником точного наведения,

расположенным в фокальной плоскости окуляра телескопа, с помощью устройства, сканирую-

щего диаграмму направленности приемника точного наведения. После перехода в режим слеже-

ния за маяком на объекте В включается лазерный передатчик с малой угловой расходимостью

луча. На следующих двух этапах объект А осуществляет ту же процедуру поиска луча передат-

чика, что и объект В при поиске маяка. После захвата приемником объекта А узконаправленного

излучения передатчика В, включается передатчик с малой угловой расходимостью луча на объ-

екте А. На последнем этапе объект В осуществляет поиск и захват сигнала передатчика А при-

емником точного наведения.

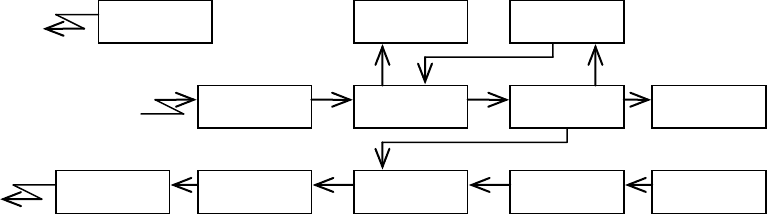
Соответствующая процедуре поиска структурная схема приемо-передатчика системы связи

на лазерах приведена на рис. 6.2.1. На рис.6.2.1 обозначены:

1) маяк с широким лучом ~10°;

2) приемник грубого поиска по углам;

3) блок сканирования диаграммы направленности приемника;

4) антенна;

5) вспомогательная антенна;

6) приемник канала автосопровождения по углам и приемник передаваемой информации;

7) оконечное устройство;

8) лазер;

9) модулятор;

10) вспомогательная оптика передатчика;

11) устройство оптического смещения луча;

12) антенна.

В целом приемопередатчик (без маяка) может быть аналогичным типовой системе лабора-

тории космической электроники Маршалловского научно-исследовательского центра космиче-

ских полетов [9, 10].

Время вхождения в связь двух объектов А и В (

) и отношение сигнал / шум q в канале

приема информации зависит от целого ряда параметров элементов структурной схемы и величи-

ны средств С, отпускаемых на создание системы.

При формализации задачи оптимизации системы необходимо использовать зависимость

С и q от основных параметров, таких как мощность лазера маяка

, мощность передатчиков

объектов А и В

1 2,

, диаметра объектива телескопа d, коэффициентов ослабления оптикой пе-

редатчиков и приемников грубого канала

i гр

и оптикой точных каналов

i т

, а также совме-

щенной оптикой

, полос приемника грубого

г р

и точного

обнаружения, произведения

числа отсчетов при обнаружении на средний относительный уровень сигнала, определенный с

учетом неточности работы системы слежения Д, квантовых входов приемников грубого

г р

точного

наведения. Далее будем обозначать

степенные монотонные функции этих пара-

метров. При наличии нескольких ограничений, накладываемых на качественные и тактические

характеристики оптической линии передачи информации самым естественным критерием при

11 10 9 8

Рис 6.2.1

104

оптимизации может быть минимальная стоимость С линии при

доп

= ≥

, обеспечивающая

выполнение требуемых качеств передачи информации и

t t

n n доп

при заданных тактических

условиях. Задача допускает двойственную постановку:

min t

при

q q

доп

≥

C C

доп

≤

Такая задача имеет более удобный для решения вид и, кроме того, представляет самостоя-

тельный интерес, т. к. время вхождения в связь в ряде случаев может являться основным пара-

метром системы, в противном случае все доводы о возможности скрытой по углам передачи

информации большого объема за ограниченное время перестают иметь смысл.

Таким образом, задача состоит в определении оптимального вектора, с компонентами

м i opt

i opt

, T

i гр opt

, T

i т opt

i opt

т i opt

гр i opt

гр i

т i

при котором достигается минимум времени поиска при заданных ассигнованиях.

( )

t f W W T T d П П

n м i т i г г т i

= , , , , , , , , , , ,

рi i i гр i гр i т i i р i i

η η ε η η

ε ε

при ограничениях

( )

q W T T d П П q

т i г допi i i т i i i

, , , , , ,

ε ≥

( )

C C W W T T d П П C C

м i т i г г т i i

доп

= =

∑

≤, , , , , , , , , , ,

рi i i гр i гр i т i i р i i

η η ε η η

ε ε

0 ≤ ≤X X

i i пред

Для решения этой задачи необходимо конкретизировать вид функции качества

и ограни-

чений в соответствии с выбранной структурной схемой и принципом действия.

6.3. Среднее время вхождения в связь

Среднее время вхождения в связь с использованием описанной выше процедуры поиска мо-

жет быть определено, например, использованием следующей методики. Описанный процесс

поиска является вероятностным процессом. Он может моделироваться конечной марковской

цепью с поглощением в предположении о малости вероятности черезэтапного перехода при по-

иске связи. Будем полагать малой вероятность ложной тревоги в процессе обнаружения сигна-

лов. В этом случае диаграмма состояния и вероятностей переходов можно изобразить в виде

рис. 6.3.1 Каждое состояние, изображенное на диаграмме, соответствует описанному выше эта-

пу поиска:

— включение маяка и направление его на объект В;

— осуществлен грубый поиск маяка на объект В, начинается поиск точной системой наве-

дения;

— осуществлен поиск точной системой наведения, включается лазер на объекте В, объект А

осуществляет грубый поиск;

— осуществляется поиск сигнала лазера В системой точного наведения объекта А;

— включается лазер на объекте А, осуществляется поиск системой наведения объекта В;

— поглощающее состояние — приемо-передатчики вошли в связь.

Стохастическая матрица вероятностей перехода Р будет в этом случае иметь вид

Рис. 6.3.1

105

a a a a a a

p p













1 2 3 4 5 6

11 12

22 23

33 34

44 45

0 0 0 0

0 0 0 0 0

0 0 0 0 0 1

. (6.3.1)

Среднее число шагов t, затрачиваемое при переходе процесса из не поглощающего состоя-

ния

в поглощающее состояние

может быть определено по формуле

t I Q C= −

−

( )

, (6.3.2)

где I — единичная матрица,

С — вектор-столбец, все компоненты которого равны единице,

а Q — матрица, получаемая из матрицы Р вычеркиванием всех строк и столбцов, соответст-

вующих поглощающему состоянию

. Тогда матрица

I Q−

будет иметь вид

( )

I Q

p p

− =

− −













1 0 0 0

0 1 0 0

0 0 1 0

0 0 0

0 0 0 0 1

11 12

33 34

44 45

. (6.3.3)

Тогда

( )( )

T I Q

p p

= − =

− − −

−













−

( )

11 22

22 33

33 44

44 55

1 1 1

0 0 0

1 1 1

0 0

1 1 1

0 0 0

1 1 1

0 0 0 0

(6.3.4)

и, наконец, матрица

( )( )

( )(

)

t TC I Q C

p p

= = − =

−

− −

−

− −

−

− −

−

− −

−













−

( )

11 22

22 33

33 44

44 55

1 1 1

. (6.3.5)

Сумма элементов вектор столбца t в данном случае определяется средним числом шагов и

есть продолжительность процесса до поглощения

при условии, если он начинается в

Учитывая, что

p p

12 11

1+ =

p p

23 22

1+ =

p p

34 33

1+ =

p p

44 45

1+ =

p p

45 55

1+ =

106

p p

55 56

1+ =

и полагая для общности, что длительность шага процесса на каждом этапе различна, среднее

время поиска или среднее время вхождения в связь может быть представлено в виде

p p p p p

= + + + + +

τ τ τ τ τ

, (6.3.6)

где

— время, затрачиваемое на первоначальное пере нацеливание в заданную точку про-

странства и различные переключения,

p p

12 1

— вероятность обнаружения маяка приемником грубого слежения,

p p p

н23 2

— вероятность обнаружения сигнала приемником точного наведения,

— вероятность того, что диаграмма приемника В направлена в требуемом направлении

(в пределах поля зрения мозаики),

p p

34 3

— вероятность обнаружения луча передатчика объекта В системой грубого поиска

объекта А,

p p p

н45 4

— вероятность обнаружения сигнала передатчика объекта В системой точного слежения

объекта А,

— вероятность того, что диаграмма приемника В направлена в требуемом направлении,

p p p

н56 5

— вероятность обнаружения сигнала передатчика объекта А системой точного слежения

объекта В,

— вероятность того, что диаграмма приемной антенны объекта В направлена в требуе-

мом направлении.

Если процедура поиска начинается с объекта В, то формула для t не изменится, однако веро-

ятности обнаружения и нацеливания будут иметь в общем случае другие значения.

Принято считать, что излучение лазера, работающего в одномодовом, стабилизированном

по мощности режиме обладает пуассоновским распределением сигнальных фотонов. Будем

предполагать, что вероятность обнаружения определяется лишь собственным, квантовым шу-

мом, аддитивным с сигналом. Это является типичным предположением при использовании оп-

тических систем с небольшим углом зрения, с узкополосными фильтрами и охлаждением при-

емников.

В этом случае вероятность обнаружения сигнала определяется как

S e

n S

n n

∑

−

∞

, (6.3.7)

где

— порог системы, величина которого может быть оценена по заданной вероятности

ложной тревоги,

— среднее число фотоэлектронов, эмитируемое фото катодом вследствие облучения по-

лезным сигналом либо маяком, либо передающим устройством объекта А или В.

Если пиковая мощность излучения оптического источника равна

, то энергия полезного

сигнала на входе приемника с учетом ослабления на трассе распространения может быть запи-

сана как

W e

i i

γ−

∏

2 2

, (6.3.8)

где

— полный коэффициент ослабления сигнала на трассе,

R — дальность между передающей и приемной системой (в дальнейшем дальность прини-

мается равной максимальной, т. е. такой, на которой еще возможно обнаружение сигнала маяка

с заданным качеством и обеспечение минимального необходимого отношения сигнал / шум в

канале приема информации),

d — диаметр приемной антенны,

— ширина диаграммы приемника грубого или точного слежения,

107

∏

— общий коэффициент передачи совмещенной оптики передатчика и приемника.

Среднее число фотоэлектронов на выходе фотоприемника запишется в виде

W e d T T

i i

i т(гр)

i i

∏ ∏

−

τ η

γ 2

2 2

Θ 

, (6.3.9)

где

i т(гр)

∏

— общий коэффициент передачи оптики приемника грубого или точного наце-

ливания,



— постоянная Планка,

— частота излучения лазера,

— квантовый выход фотоприемника.

Величина

нi

в формуле (6.3.6) определяется следующим образом

нi

≅













р i

, (6.3.10)

где

р i

= .

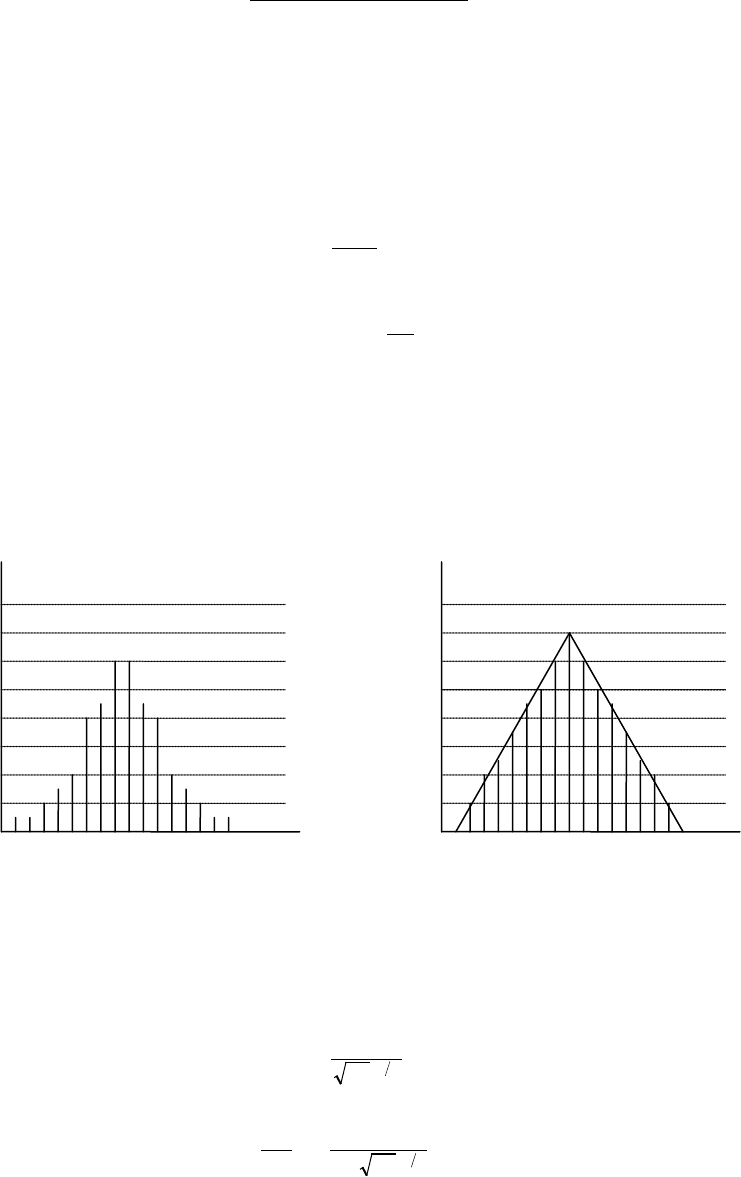
Вероятность обнаружения сигнала, представленного в форме (6.3.7), имеет достаточно

сложный вид, что делает ее неудобной для последующего решения задачи нахождения опти-

мальных характеристик системы. Вместе с тем, уже при

S = 10

распределение закона Пуассона

будет иметь вид рис. 6.3.2 и вероятность обнаружения сигнала с ошибкой ≤ 25 % может быть

аппроксимирована ломаной εВСД рис. 6.3.3. При числе сигнальных фотоэлектронов ≥ 100, что

характерно для режима передачи информации с большой скоростью, эта ошибка будет незначи-

тельной.

Если ограничиться указанной аппроксимацией, то вероятность обнаружения сигнала может

быть представлена как

= −1

3 2



. (6.3.11)

Подставляя (6.3.11) в (6.3.6), получим выражение для среднего времени поиска в виде

p S

н j

j i

н j

∑

= =

τ τ

3 2

. (6.3.12)

Для дальнейших расчетов предположим, что приемо-передатчик системы лазерной связи

идентичны. Кроме того, из естественных конструктивных соображений и из анализа принципа

работы системы следует

Рис. 6.3.2

P(n)

0.16

0.12

0.08

0.04

S=10

Рис. 6.3.3

S=10

P(n)

0.16

0.12

0.08

0.04

108

τ τ

1 3

τ τ τ

2 4 5

= =

p p

н н

1 2

p p

н н

3 1 2

. (6.3.13)

Тогда, подставляя уравнение (6.3.10) и (6.3.11) в (6.3.12) с учетом (6.3.13) и принятого пред-

положения об идентичности приемо-передатчиков лазерной системы выражение для

примет

вид

t K

m П

K K

d T

n П

m T

W W

г г

i гр г

т т

i т

= +













∏













∏













∏





































2 2

1 2

3 2

2 1 2

3 2

2 2 1 2

3 2 3 2 3 2

р р

Θ Θ

ε η η

, (6.3.14)

где

−

ν

K П

i i2

= τ

г т

гр(т)

р( )

6.4. Отношение сигнал/шум на выходе системы обработки информации

Далее необходимо конкретизировать ограничение на отношение сигнал / шум, обеспечивае-

мое системой в момент передачи информации. Предположим, что по каналу передается инфор-

мация. При условии ранее принятых ограничений на характер шумов системы, отношение сиг-

нал / шум на выходе системы прямого детектирования, содержащей приемник с внутренним

коэффициентом по току согласно [10], определится как

eFП

п м

, (6.4.1)

где µ — коэффициент модуляции света,

W S П

п мр

= ν

, (6.4.2)

п мр

— величина мощности сигнала на выходе фотоприемника,

e — заряд электрона,

F — коэффициент, учитывающий увеличение шума в процессе внутреннего усиления,

— полоса канала приема информации.

Подставляя (6.4.2) в (6.4.1) и используя соотношение (6.3.9) для среднего числа фотоэлек-

тронов при приеме излучения передатчика, получим

( )

e W T T Д

П R

ти

i i

ти m

∏ ∏













−

µ η η

2 2

тi

 Θ

. (6.4.3)

6.5. Формализации задачи оптимизации лазерной линии связи

Как отмечалось в предыдущих разделах 3, 4, существует высокая корреляция, либо даже

функциональная зависимость стоимости линии передачи информации от ее основных парамет-

ров.

Обладая ценными качествами, такими как аддитивность и измеримость («тождество эффек-

та»), стоимость вполне может служить самостоятельным критерием качества, описывающим

всю систему, несмотря на разнородность ее элементов.

Поскольку, вообще говоря, стоимость известных линий передачи информации того же клас-

са является случайной, для задачи следует применять в качестве ограничений по стоимости ли-

нии среднеквадратической регрессии стоимости на параметры.

Таким образом, стоимость линии связи С может быть записана в виде многомерной функ-

ции.

( )

C C X X X

1 2

, , ,

. (6.5.1)

109

Свойство аддитивности позволяет представить (6.4.4) почти для всех блоков (рис. 6.1) сле-

дующим образом

( )

C C X

i i

∑

. (6.5.2)

Функции

( )

C X

i i

представляют собой монотонные функции от прямо определенных техни-

ческих параметров, т. е. таких, при увеличении которых качество системы улучшается, а стои-

мость растет. Однако, даже в виде (6.5.2) использовать зависимость

( )

C X X

, ,

неудобно по

следующим причинам:

( )

C X

i i

— произвольные линейные зависимости различного вида,

( )

C X

i i

меняется от времени, от серии к серии, от изделия к изделию,

( )

C X

i i

— зачастую неизвестные функции ввиду возможного отсутствия статистики.

Действительно, хотя

( )

C X

i i

нам заранее, возможно, и неизвестны, задачу желательно ре-

шить в общем (аналитическом) виде, куда затем при наличии статистики можно было бы под-

ставлять готовые данные и получать готовые оптимальные решения. С целью устранения недос-

татков 1—3 и получения при произвольных и неизвестных

( )

C X

i i

решения в общем виде (в

квадратурах), линеаризуем

( )

C X X

, ,

в окрестности такого вектора параметров



, который

наиболее часто используется в подобных линиях передачи информации того же класса. Такой

выбор вектора параметров играет роль использования априорных сведений об оптимальном ре-

шении.

При этом

C B C X

i i

∑

′

∑

= =1

, (6.5.3)

где

B C C X

i i i i

= −

′

0 0

Кроме ограничений по стоимости на технические параметры наложены ограничения, свя-

занные с их технической выполнимостью. Например, мощность непрерывного излучения лазера

ограничена снизу 0, а сверху — предельной (максимальной) мощностью, которую уже можно

получить к моменту создания проекта.. Ограничения на параметры по условиям физической

реализуемости можно записать в виде

0 ≤ ≤X X

i i пред

. (6.5.4)

Таким образом, вводя формальные («фазовые») параметры

, которые являются монотон-

ными прямо определенными функциями от соответствующих технических параметров, а также,

учитывая соотношения (6.4.6), (6.4.14), (6.4.3), (6.5.4) можно представить задачу в формализо-

ванном виде:

{ }

C B C X

i i

∑

′

∑













= =

min

t K

K K

X X

= +













∏













∏













1 1

1 2

3 4

, (6.5.5)

1 1

X q

доп

∏

≤

0 ≤ ≤X X

i i пред

где

eF R

ти

−

ν

µ η

110

6.6. Решение задачи оптимизации лазерной линии связи

Задачу выпуклого программирования (6.5.5) оптимизации лазерной линии связи весьма

удобно решать методом динамического программирования в общем виде, используя при этом

решения, полученные в [23]. Используя принцип двойственности, задачу можно сформулиро-

вать также в виде

{ }

min

t K

K K

X X

= +













∏













∏

























1 1 1

1 2

3 4

, (6.6.1)

1 1

X q

доп

∏

≤

, (6.6.2)

B C X C

i i

i c

= =

∑

′

∑

≤

min

, (6.6.3)

0 ≤ ≤X X

i i пред

. (6.6.4)

Идея решения будет заключаться в следующем. Поскольку мы имеем дело с сепарабельным

программированием [22], будем искать решение для целевой функции (6.6.1) при ограничениях

по стоимости (6.6.3). При этом целесообразно искать

min t

последовательно по группам пара-

метров, а затем между группами, перераспределяя ассигнования. В результате этого решения

будут определены оптимальные параметры системы, которые удовлетворяют лишь двум услови-

ям (6.6.1), (6.6.3). Если какие-либо параметры не удовлетворяют условиям (6.6.2), (6.6.4), то они

принимаются равными предельным значениям и фиксируются. Задача решается снова для ос-

тальных параметров. Полученные оптимальные значения следует подставить в условие (6.6.2).

Если оптимальные параметры удовлетворяют условию качественной передачи информации

(6.6.2), то они являются оптимальным решением для трех условий задачи. В случае если пара-

метры, оптимальные по условиям (6.6.1, 6.6.3) не удовлетворяют условию (6.6.2), оптимальные

решения следует искать на гиперповерхности, (6.6.3), т. е. путем уменьшения степени свободы

целевой функции при подстановке (6.6.2) в (6.6.1), когда накладываются дополнительные связи

на параметры. При этом, безусловно, величина

min t

несколько возрастает и возможна также

полимо дальность (6.5.5).

Определим (6.6.1) при ограничениях (6.6.3).

1-й шаг:

min

∏

′

∏

, (6.6.5)

′

∑

≤

C X C

i i

э02 2

i opt

′

2-й шаг:

min

∏

′

∏

, (6.6.6)

′

∑

≤

C X C

i i

э03 3

i opt

′

3-й шаг:

( )

min

C С

А А

э э

23 2

−

























, (6.6.7)