Алешин Г.В., Богданов Ю.А. Эффективность сложных радио-технических систем
Подождите немного. Документ загружается.


УДК 621.396.6
ББК 32.841
А57
Рекомендована а печати ученым советом УкрГАЖД
(протокол №1 от 25.02.08г. г.Харьков)
Рецензенты: Ю.И.Лосев доктор технических наук профессор (ХУПС)
П.Ю.Костенко доктор технических наук профессор (ХУПС)
Алешин Г.В., Богданов Ю.А.
Эффективность сложных радиотехнических систем. - Киев 2008.-,
В книге изложены как общие принципы практической постановки и решения задач
оптимизации радиотехнических систем, так и методы их решения по условным критериям
качества, которые представляются как наиболее объективные. При этом рассматриваются
задачи оптимизации систем различных диапазонов волн на трех иерархических уровнях:
подсистем, систем и «больших систем», или комплексов. Применительно к
информационно-измерительным системам, изложенные в общем виде оптимальные
решения можно с некоторыми допущениями считать решением проблемы их
оптимального синтеза на множествах технических параметров, измерительных структур и
частично сигналов.
Студентам, аспирантам, инженерам и научным работникам в области
радиотехнических систем книга может служить пособием в постановке и решении
конкретных и общих научных и технических задач в создании сложных, но эффективных
систем.
Книга позволяет инженерам понять законы оптимальности технических решений для
повышения эффективности эксплуатируемых систем.
ББК 32841
Иллюстраций-64, таблиц-1, библиография-45 наименований.
)(
С
Г.В. Алешин, Ю.А.Богданов,
«Наукова думка», 2008
3
Эффективность сложных радиотехнических систем
Введение
Несмотря на широкое развитие математических методов и теорий оптимизации сложных объектов,
ситуаций, процессов и т. д., у специалистов, особенно радиотехнического направления, всегда остается
чувство неудовлетворенности, связанное либо с неадекватностью принятой модели реальным объектам и
пр., либо с неразрешимостью задач. Другими словами, излишняя абстрактность системных задач, для
которых имеется широкий парк математических постановок и их решений, с одной стороны, не позволяет
учесть все особенности сложных радиотехнических систем, с другой стороны, излишняя конкретизация
таких задач приводит к их практической неразрешимости, ввиду многомерности, многокритериальности и,
как специфики радиотехники, стохастичности. Даже если такие задачи разрешимы, то пользы от такого
частного (числового) решения практически никакой, поскольку маловероятно, что специалисту понадобятся
именно эти числовые значения технических требований. Для других технических требований неизвестно,
как поведет себя решение. А для любых технических требований необходимо всякий раз решать
конкретную числовую задачу, даже тип которой может существенно изменяться в зависимости от исходных
данных, самыми неопределенными из которых являются технико-экономические показатели.
Игнорирование и неучет технико-экономических зависимостей равносилен самообману для
разработчика систем, который все равно вынужден эвристически их учитывать. А учет технико-
экономических зависимостей с неизбежностью приводит к глобальным (всеохватывающим) для РТС
ограничениям, а, значит, к появлению глобальной оптимальности, связанной с оптимальным
распределением усилий (затратных показателей) системы в создании и качестве эффекта ее
функционирования.
В книге предложены пути разрешения этих трудностей.
В сочетании с новой измерительной идеологией, связанной с учетом широкого априорного диапазона,
оперативности и затратных показателей, с новыми подходами в оценке эффективности (качества) РТС, с
новыми методами постановок и решения задач оптимизации РТС, изложенными в работе, системные идеи
дают более полное представление об РТС и об их эффективности.
Разнообразие задач оптимизации систем на всех уровнях их иерархии расширяют возможности
применения результатов для решения конкретных задач.
Как и любые задачи управления качеством, такие задачи наиболее полезны для использования на этапе
эскизного проектирования вновь создаваемых РТС. Полезны они и для оценки эффективности
существующих систем при определении направлений их модернизации или совершенствования систем в
новых поколениях.
Сложные информационно-измерительные радиотехнические системы (ИИРТС) являются по
определению многофункциональными и многоканальными с однородными и неоднородными каналами. Их
качество практически всегда описывается вектором показателей, которые определяются назначением
системы и условиями их создания и функционирования. В работе представлены методы общего решения
проблемы синтеза Парето-оптимальных ИИРТС [1,2] с учетом вектора показателей качества на множествах
технических параметров.
Проблемы, препятствующие оптимальному синтезу ИИРТС
Получению оптимального решения таких задач оптимального синтеза препятствуют следующие
проблемы:
1) разнообразие и многофункциональность требуемых ИИРТС и обычная для них трудность выбора
единого адекватного критерия и полнота (представительность) критерия;
2)большая размерность вектора технических параметров – «проклятье многомерности»;
3)многообразие условий функционирования ИИРТС;
4)наличие случайных и даже нечетких (например, стоимость) параметров и факторов;
5)оптимальный синтез ИИРТС должен осуществляться на множествах технических параметров,
сигналов и структур;
6) отсутствует единый метод оптимизации ИИРТС, поскольку алгоритм решения существенно зависит
от метода, формы показателей и постановки задач синтеза.
7)отсутствуют решения многих задач системного анализа для широкого парка многофункциональных
систем, то есть, задач получения зависимостей показателей качества ИИРТС от ее технических параметров,
необходимых для оптимального синтеза систем;
8)необходимость выполнить условие Слейтера [4], убедиться в том, что множество допустимых
решений непусто, условия одномодальности, единственности решения, выпуклости, вогнутости, условие
сходимости решения и другие условия;
9)отсутствуют идеи и предложения для решения задач синтеза совмещенных систем, в том числе задачи
оптимального аппаратурного и сигнального совмещения;
10)требуется найти связь задач оптимизации с технологичностью систем и функциональных элементов;
11)требуется преодолеть двойственность решений многокритериальных задач;
4
12)поскольку одно полученное оптимальное решение дает мало информации о поведении оптимальной
системы, о критичности оптимума, о вариантах построения и так далее, требуется широкий диапазон
решений для построения «кривой обмена» [2], которая позволяет оценить качество систем данного класса.
Краткая характеристика решений проблем синтеза ИИРТС
По первой проблеме: разнообразие требуемых ИИС преодолевают индивидуальной постановкой и
решением задач синтеза конкретных ИИРТС, а в качестве единого критерия чаще выбирают взвешенный
или относительный критерий качества, реже – условный критерий качества. В работе [1] показано, что при
заданном векторе показателей качества наибольшей объективностью обладает условный критерий качества
(в виде математического программирования). Причем, ресурсные ограничения имеют в ИИРТС
равноправный характер. Все показатели качества должны быть представлены в виде экстенсивных
физических величин. Если последнее условие не выполняется, то рекомендуется ограничивать размерность
вектора технических параметров за счет набора статистики лишь для систем достаточно узкого класса,
например, для бортовых ИИРТС, для данного диапазона волн и так далее. Многофункциональность
приводит к усложнению проблемы отыскания собственных чисел в методе множителей Лагранжа.
Для синтеза многофункциональных ИИРТС и решения второй проблемы возможна унификация формы
представления показателей качества и решение задач блочным методом {1,45] или методом динамического
программирования.
Третья и четвертая проблемы вынуждают использовать известные и отыскивать новые закономерности
влияния условий функционирования ИИС и характера параметров и факторов на критерий качества ИИРТС.
В значительной степени это относится к различным понятиям стоимости, которую скорее можно отнести к
нечетким множествам, но без которой при системном подходе обойтись нельзя. С нечеткостью стоимости
предлагается бороться следующим образом:
1)Для известных систем того же назначения, но с различными значениями тактико-технических
требований, для требуемого состава функциональных элементов (ФЭ), отображаются на плоскости или в n-
мерном пространстве (маркетинговые) данные по технико-экономическим параметрам ФЭ. Эти
статистические данные собираются по возможности по всем комплектующим ФЭ.
2)Все технические параметры должны удовлетворять требованиям: чем их значения меньше, тем лучше
для ИИРТС. Если такое условие для какого-либо параметра не выполняется, то производят его монотонное
преобразование с тем, чтобы условие выполнялось. Например, можно взять обратно пропорциональную
величину.
3)Зная все зависимости показателей качества ИИРТС от параметров, уже можно представить задачу ее
оптимизации как задачу дискретного программирования. При этом ее можно упростить, если отобрать лишь
те параметры на плоскости «цена ФЭ - технический параметр», или в соответствующем пространстве,
которые ближе к осям координат. Отбраковываются ФЭ, имеющие спекулятивные цены.
4) Поскольку задачи дискретного программирования большой размерности не самые лучшие,
оставшиеся после отбраковки данные сглаживаются линиями среднеквадратической регрессии цен на
параметры малого порядка. Это дает следующие преимущества: упрощается задача, ускоряется алгоритм
решения, появляется возможность математического анализа устойчивости и критичности оптимального
решения, прогноза его динамики, определения перспективных направлений в развитии систем и их ФЭ, в
оценке технологичности ФЭ и т.д.
Пятая проблема, также как и первая, решается последовательно по частям. Известен банк отдельных
задач оптимального синтеза сигналов, в основном для двух показателей качества, алгоритмов, структур и
параметров - для двух-трех показателей качества. Однако для более полного состава вектора показателей
качества, который обычно представлен в тактико-технических требованиях к системе, требуется разработать
оптимальный синтез ИИРТС на трех множествах: параметров, сигналов и структур.
Шестая проблема может быть решена специальным методом [45], обобщающим метод Вульфа, и
предполагающим монотонные преобразования координат, или преобразования технических параметров в
фазовые, сведением задачи к сепарабельной, получением итеративных соотношений для поиска
оптимальных решений.
Седьмая проблема решается расширением парка известных зависимостей показателей качества ИИРТС
от технических параметров [2,12,45 и др.] и применением ограничительного условия близости модели
системы, или процесса, к идеальной [1].
Восьмая проблема обычно решается за счет эволюционного пути развития систем, который использует
преемственность поколений систем и опирается на известный «базовый» вариант системы, на имитационное
моделирование и так далее.
Девятая проблема может быть решена лишь в результате системного анализа уже полученных
оптимальных решений. Для этого целесообразно иметь также семейство оптимальных решений задач
оптимизации для получения «кривых обмена» [2].
Десятая проблема может быть решена применением специального метода обработки статистических
технико-экономических данных [45].
Одиннадцатая проблема может быть решена, если принять во внимание основные свойства реальных
систем.
5
Двенадцатая проблема решается после многократного решения задач синтеза систем при варьировании
условий постановки задач.
Сложные ИИРТС обычно являются совмещенными системами. Аппаратурно совмещенными называют
такие системы, которые одной и той же аппаратурой, или частью ее, обрабатывают общий сигнал,
позволяющий системе выполнять одновременно несколько различных функций или назначений системы.
Кроме аппаратурного используют также сигнальное совмещение. Сигнальным называется такое его
совмещением, которое позволяет в одном сигнале передавать и принимать различную информацию,
предназначенную для выполнения нескольких функций системы. Совмещенная аппаратурно и (или)
сигнально система может практически одновременно производить прием, обнаружение сигнала, измерение
одного или нескольких параметров сигнала, передачу станционной либо бортовой телекоммуникационной
многоканальной информации, передачу данных, в том числе телеметрических данных. Ввиду дороговизны
линий связи либо аппаратуры радиотехнического диапазона, особенно антенн, передатчиков, фидеров,
преселекторов, преобразователей и радиоусилителей, а также ввиду удобства одновременного
использования одного электрического или электромагнитного контакта с абонентом, системы
предпочтительнее совмещенные, поскольку они более эффективны. Аппаратурное совмещение особенно
удобно при достаточно широкой полосе линий связи и аппаратуры соответствующего диапазона волн.
Сигнальное совмещение, создание группового сигнала, и его обработка могут оказаться значительно
сложней ввиду возникновения проблемы борьбы с взаимными помехами, проблемы ЭМС. Для совмещения
и разделения сигналов с заданным качеством используются следующие параметры селекции: частота, время,
структура сигнала или составляющие его спектра, а иногда - параметры поляризации. Разделенные части
общего сигнала поступают в соответствующие каналы системы для обработки (рис. 1). Сечение, где
разделяется сигнал по каналам, обычно работает с более низкими частотами, используемыми в
совмещенном сигнале, даже в радиотехническом диапазоне. При этом разделение не обязательно должно
быть в одном сечении системы, хотя это весьма удобно.
Решение проблемы оптимального построения совмещенных систем состоит в том, чтобы учесть
аппаратурное и сигнальное совмещение при формализации задач, сформулировать задачи, учесть основные
показатели качества, решить задачи и получить рекомендации о выборе лучшей структуры систем, о
технических параметрах и о сигналах на соответствующих множествах. Для этого необходимо по
возможности использовать все показатели, входящие в тактико-технические требования к системе и все
ограничительные условия, в том числе ресурсные ограничения. При создании ИИРТС, особенно при
рыночной экономике, технические и ресурсные показатели фактически имеют равноправный характер, что и
следует учитывать в задачах их синтеза.
Математические теории оптимизации многокритериальных систем достаточно развиты [1,22 и др.], и
известны задачи оптимизации ряда ИИРТС [10,22 и др.], однако возможно и целесообразно, используя
специфику ИИРТС, создать по возможности унифицированный метод их оптимизации.
6
1. Основы принятия оптимальных решений при разработке радиотехнических систем
1.1. Принятие простых решений о лучшей системе
Вся человеческая жизнь практически во всех сферах деятельности связана с проблемой
выбора лучшего варианта (любой природы) среди имеющихся. Даже простой выбор лучшего из
двух вариантов, который является простейшей задачей оптимизации, может значительно
усложниться в зависимости от того, что понимать под термином «лучший», сколько показателей
качества описывают варианты, насколько точно (адекватно) они их определяют, как точно
оценивается результат сравнения и т. д.
Проблему выбора оптимального варианта или связанного с этим оптимального решения,
целесообразно рассматривать от простого к сложному согласно принципам Декарта. Напомним,
что таких принципов пять:
1) не торопиться в суждениях;
2) избавляться от предвзятых мнений;
3) делать по возможности более полные обзоры того, что сделано предшественниками;
4) каждый вопрос разлагать на более простые;
5) начинать решение от простого к сложному.
По существу, такие принципы являются гносеологической основой эффективности
достижения цели. Пятый принцип согласуется с известным еще со средних веков принципом
францисканца У. Оккама: «Не следует умножать число сущностей сверх необходимости».
Данный принцип носит еще название «бритвы Оккама». Смысл его в том, что при чрезмерном
усложнении модели результата, скорее всего, не будет — он будет «обрезан». О существовании
нижней и верхней границ сложности на каждом этапе рассмотрения говорит принцип Р.
Беллмана: «Исследователь подобен путнику, идущему по узкой тропинке между западней
переупрощения и болотом переусложнения».
Значит, даже сам подход к решению проблемы эффективности также представляет собой
задачу оптимального выбора, или оптимизации. Постепенное усложнение модели исследований
(пятый принцип Декарта) должно служить цели приближения ее к сущности, реальному объекту,
явлению, т. е. отвечать требованиям ее адекватности.
Итак, опишем понятие «лучший», пользуясь пока простейшим представлением об этом.
Будем считать вариант лучшим, если у него лучше какое-либо, по возможности, основное
качество при одинаковых прочих. Однако, «наука начинается с тех пор, как начинают измерять»
(Д. И. Менделеев). А для измерений необходимо, чтобы качество оценивалось количественно.
Количественную характеристику качества называют показателем качества. Известные способы
приведения величин к количественным значениям, метод экспертных оценок, метод реперных
точек и т. д., приложимы также для показателей качества.
Для определенности будем считать, что меньшему значению показателя качества
соответствует лучшее качество. Если фактически зависимость противоположная, то взяв,
например, обратную величину показателя качества в качестве другого показателя, можно
привести зависимость к требуемой. Очевидно, что такая зависимость должна быть монотонной,
чтобы исключить многозначность оценивания качества.
Если показатели качества двух вариантов (
D
1
и
D
2
) заданы или оцениваются точно, то
лучшим вариантом, системой и т. д., из выбираемых является тот, для которого этот показатель
меньше.
Заметим, что как и процессы оценивания показателей
D
1
и
D
2
, их сравнение является
также процессом измерений. Алгоритм дуального выбора прост: если
D D
1 2
<
, то оптимальное
решение по этому показателю есть первый вариант, и наоборот.
В случае оценки или задания показателя двух вариантов
D
1
и
D
2
с ограниченной
точностью алгоритм усложняется. Пусть
p D
1 1
( )
и
p D
2 2
( )
— соответственно плотности
распределения вероятности оценки значений показателя
D
1
и
D
2
. Пусть они симметричны.
Тогда алгоритм принятия решения можно представить в виде рис. 1.1.1. Т. е., если выполняется
следующее неравенство, то вариант 1 предпочтительней.
D D
01 1 1 02 2 2
+ ≤ −β σ β σ
(1.1.1),
где:
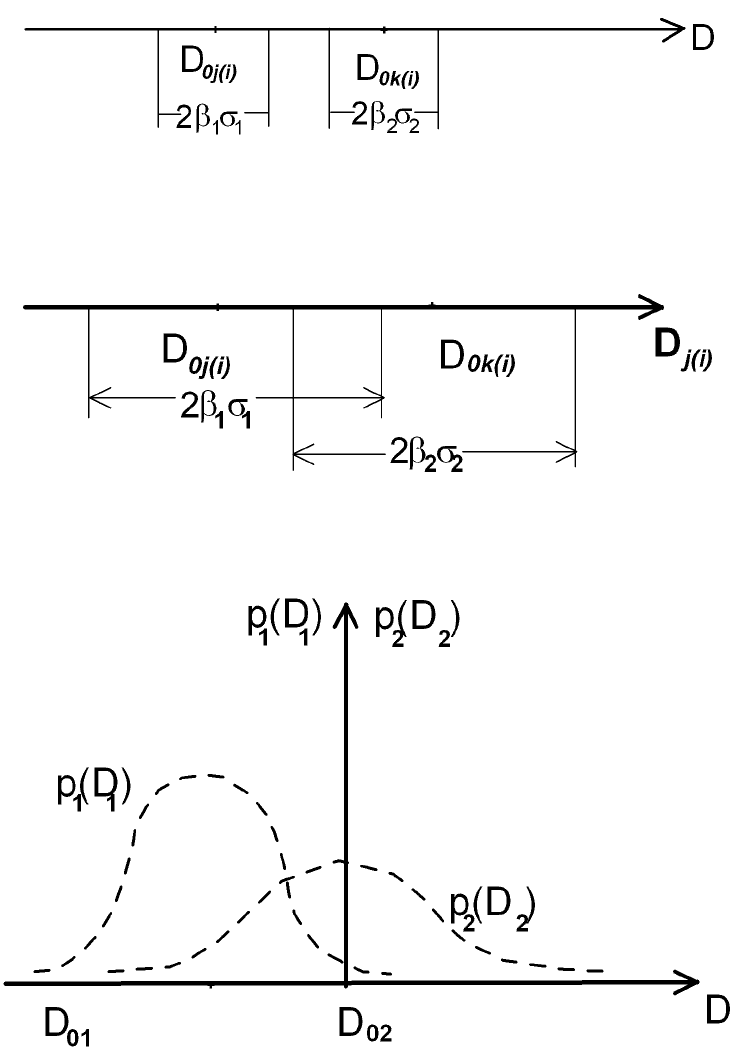
7
σ
1
и
σ
2
— соответственно среднеквадратические погрешности распределений
p D
1 1
( )
и
p D
2 2
( )
,
Рис. 1.1.1.
Рис. 1.1.2.
Рис. 1.1.3.
D
01
и
D
02
— математические ожидания значений
D
1
и
D
2
,
β
1
и
β
2
— относительные квантили указанных распределений, определяющие доверие к
решению.
Надежность, или степень доверия к такому решению соответствует доверительным
вероятностям
p
1 дов
и
p
2 дов
, где
p p D dD
i дов i i i
D
D
i i i
i i i
=
∫
−
+
( )
0
0
β σ
β σ
.
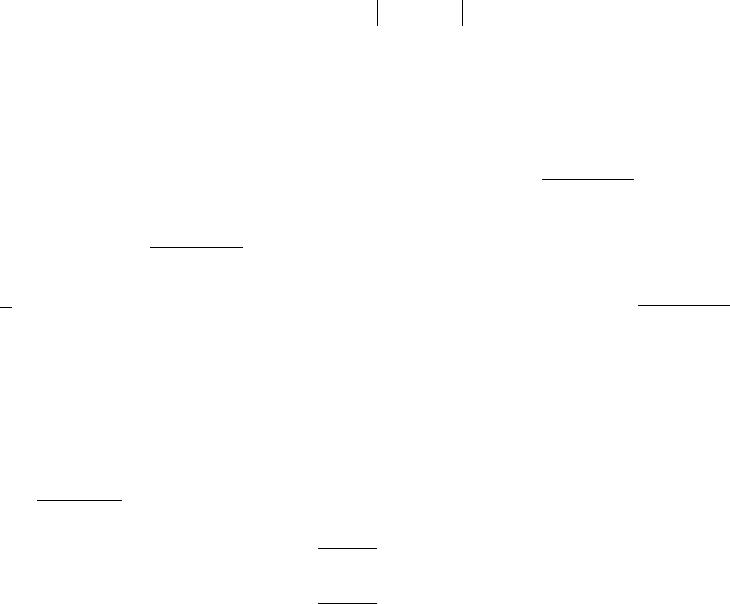
8
В случае, если доверительные интервалы
2
1 1
β σ
и
2
2 2
β σ
перекрываются (рис.1.1.2),
особенно при больших
β σ
i i
и при малой разности
D D
02 01
−
, то сравнивать варианты можно
только в среднем, или при малых доверительных интервалах, т. е. с меньшей надежностью
выводов и если известны распределения показателей качества (рис.1.1.3).
В этом случае вероятность F того, что
D D
1 2
≤
равна
F D D p D dD
D
( ) ( )
1 2 1 1 2
1
≤ =
∫
∞
.
С учетом априорного распределения
p D
1 1
( )
средняя вероятность
F D D
D
( )
1 2
1
≤
запишется
следующим образом
F D D p D p D dD
D
D
( ) ( ) ( )dD
1 2 1 1 2 2 2 1
1
1
≤ =
∫ ∫
−∞
∞ ∞
, (1.1.2)
где
F
D
1
— означает среднее по вероятности на множестве
D
1
. Если
F D D
D
( )
1 2
1
≤
существенно больше значения 0,5, то принимается решение
D
1
, в противном случае —
D
2
, т. е.
в расчете на редкость в среднем случае промахов. При равновероятных случаях
противоположных неравенств выбор безразличен.
При равных квантилях и дисперсиях распределений
p D
1 1
( )
и
p D
2 2
( )
неравенство
D D
01 02
<
обеспечивает решение с доверием к нему, которое можно оценить следующим
образом при
D D
02 01
2
−
≤ βσ
p p D dD
дов
D D
D D
=
∫
−
−
1 1 1
2
2
01 02
02 01
( )
.
Рассмотрим случай, когда каждый вариант, система или сущность, описывается множеством
показателей качества, которые оцениваются или задаются достаточно точно. В этом случае
говорят об n-мерном векторе показателей качества
D D D
n
T
= { , , }
1
. Методы, использующие
совокупность, или вектор показателей качества для поиска оптимальной системы, иногда
называют векторной оптимизацией. Строго говоря, эти методы должны содержать алгоритмы,
позволяющие получать оптимальное решение о показателях качества в виде вектора. Однако
известен постулат математического программирования о том, что некорректно ставить задачу об
оптимальности всей совокупности показателей качества. Следует требовать оптимальности для
одного показателя при заданных других. Отсюда следует, что векторная оптимизация
проблематична, что следует использовать методы «скаляризации» задач, т. е. методы
предполагающие использование показателей отдельно, и что поэтому термин «скаляризация» не
несет существенной смысловой нагрузки.
Сложные системы почти всегда описываются вектором показателей качества, поскольку
качество системы определяется показателем результата действия системы и затратным
показателем, который следует считать равноправным первому. В сложных случаях
используются совокупности таких показателей и других ограничений по условиям применения
систем.
Сравнение качества систем может осуществляться непосредственно сравнением векторов
качества
D
1
и
D
2
.
Пусть
D D
1 2
<
. Это означает, что каждая компонента вектора
D
1
не больше (лучше), чем
соответствующая компонента вектора
D
2
. Тогда ясно, что система 1 лучше, чем система 2.
Такой критерий, т. е. правило определения лучшей системы, называется критерием Парето [1,2].
Этот критерий называют безусловным критерием предпочтения. Он имеет тот недостаток, что
принятие решения о лучшей системе невозможно, если хотя бы одна компонента одного вектора
D
i1( )
больше соответствующей компоненты другого вектора
D
i2( )
, а какая-либо компонента
вектора
D
j)1(
меньше, чем соответствующая компонента вектора
D
j)2(
.
Иными словами, в этом случае системы несравнимы. Понятно, что системы несравнимы
также, если размерность векторов
D
1
и
D
2
неодинакова.

9
Если показатели качества системы, операции или другой сущности, неравноценны, то этот
случай называют лексикографическим критерием качества [1]. Ранжировку по важности
показателей качества, которые называют иногда критериями качества, производит лицо,
принимающее решение. В этом случае лексикографических критериев качества сравнение
систем, операций и т. д. возможно и в случае векторов
D
1
и
D
2
неодинаковой размерности,
если отсутствующая компонента вектора показателей качества имеет наименьшую, или малую,
значимость. Лексикографические критерии не являются предметом рассмотрения данной книги,
поскольку основные показатели качества технических систем как правило равноценны. А
неосновные рассматривать не будем.
Под условным критериям предпочтения (УКП) [2] понимается один из следующих методов:
1. Метод, основанный на введении результирующего показателя качества;
2. Минимаксный метод;
3. Перевод всех показателей качества за исключением одного в разряд ограничений;
4. Метод последовательных уступок [2];
5. Комбинированные методы.
Метод последовательных уступок относится к лексикографическим критериям качества.
Поэтому применительно к системам с равноценными показателями качества он рассматриваться
не будет.
Минимаксный метод может использоваться для построения систем с неизвестными
условиями функционирования. Основная проблема в постановке такой задачи — это получение
платежной матрицы. Да и решение такой задачи эффективно только в худшем случае, что
весьма расточительно. Поэтому этот метод также не будет рассматриваться.
Как будет видно из дальнейшего, перевод всех показателей кроме одного в разряд
ограничений является частным случаем метода, основанного на введении результирующего
показателя качества.
Отсюда следует, что нельзя считать удачной терминологию безусловного и условного
критериев предпочтения (БКП и УКП) в том понимании, как это сделано у Парето и в [2].
Если компоненты векторов
D
1
и
D
2
могут быть случайными величинами с известными
законами распределения
p D
i i1 1
( )
и
p D
i i2 2
( )
, то принятие решения о лучшей системе последует
после вычисления вероятности того, что
D D
i i1 2
≤
(для каждой компоненты), т. е.
F D D p D dD
i i i i i i
D
( ) ( )
1 2 2 2 2
1i
≤ =
∫
∞
и средней вероятности компонент
F
D D p D p D dD dD
i
i i
D
i i i i i i
D
( ) ( ) ( )
1 2 1 1 2 2 2 1
1i
1i
≤ =
∫∫
∞
−∞
∞
. (1.1.3)
Если все средние вероятности компонент существенно превышают значение
1 2
, то
D
1
в
среднем лучше, чем
D
2
, а если значительно меньше
1 2
, то лучше
D
2
. Если одна компонента
D
1
более вероятна, чем
D
2
, а другая наоборот, то решение принимать нельзя: нужна
дополнительная информация.
Распределения показателей качества
D
i1
и
D
i2
могут быть неизвестны. В значительной
степени их могут заменить гистограммы, статистические ряды и статистики, полученные в
результате сбора данных о существующих системах того же назначения и тех же типов (1 или 2).
Чаще всего эта статистика настолько бедна, что используются, так называемые, постулируемые
«логистические» распределения или просто математические ожидания
D
i
D
1
1i
и
D
i
D
i
2
2
, или
средние статистические. Это тоже информация, если другой нет, хотя она и не страдает
достоверностью. «Логистические» кривые определяют опытные специалисты — эксперты,
которых нельзя обвинить в отсутствии интуиции.
Для случая сравнения средних
1 1
1 2
11
m
D
k
D
ij ij
l
k
j
m
≤
∑∑
==
, где
j m∈[ , ]1
,
l k∈[ , ]1
.
Для известных частот
D
i1
и
D
i2
10
F D D
m
m
i i i
ij
j
l
ij
j
k
( )
1 2
2
1
2
1
≤ ≈
∑
∑
=
=
, где
m
ij2
— частота появления
D
i2
в j-м интервале
∆D
i2
, и
F D D
m m
m
i i i
D
il
l
q
ij
j
l
ij
j
k
( )
1 2
1
0
2
1
2
1
1i
≤ ≈
∑ ∑
∑
= =
=
,
где
m
il1
— частота появления
D
i1
в l-м интервале
∆ ∆D D
i i1 2
=
.
Однако даже при четко заданных
D
i1
и
D
i2
∀ ∈i n[ , ]1
, где n — размерность
D
1
и
D
2
, и
выполнении неравенства
D D
1 2
≤
нет уверенности в том, что система, обладающая
характеристиками
D
1
, хотя бы близка к оптимальной.
Такая уверенность может появиться, несмотря на то, что до сих пор это считается большой
проблемой, если использовать дополнительную информацию о показателях качества системы и
методы оптимизации систем, предлагаемые далее.
1.2. Иерархичность радиотехнических систем и принятие сложных решений об их
параметрах
Уверенность в том, что система достаточно близка к оптимальной появляется в результате
решения задач оптимизации системы. Однако этому предшествует этап постановки задач. В
конечном счете, как постановка такой задачи, так и ее решение является в значительной степени
своего рода искусством, причем, литература по радиотехнике не изобилует такими примерами.
Однако при некотором опыте можно заметить ряд устойчивых свойств таких задач, что является
основой для выявления соответствующих законов природы в оптимизации систем.
Уверенность в оптимальности системы, описываемой вектором
D
1
, появляется лишь тогда,
когда становятся известными зависимости
D X
i1( )
( )
, необходимые для решения задач
оптимизации. Под
X
понимается вектор технических параметров данной системы. Следует
заметить, что существует иерархия систем по классификации решаемых ими задач. На самом
нижнем уровне иерархии систем располагаются радиоэлектронные детали, затем следуют узлы,
каскады, далее — функциональные элементы системы, собственно системы, далее — комплексы
систем, группировки комплексов, возможно, сети, отрасли и т. п. Уровни определяются в
известной степени условно, хотя чаще всего они разделяются также конструктивно.
Под системой можно понимать один или несколько из указанных уровней, объединяемых
целью, или целями функционирования. Система характеризуется качеством достижения целей, а
в отношении структуры — уровнем детализации. Функциональные элементы системы являются
в свою очередь системами более низшего уровня и т. д. Качество достижения цели может
описываться вероятностью достижения цели, которая зависит от показателей качества
D X( )
.
Поскольку определение такой вероятности чаще всего невозможно, то описание качества
достижения цели функционирования систем ограничивается вектором показателей качества
D X( )
. Физическая сущность технических параметров
X
определяется уровнем детализации
системы. Опыт создания систем и решения задач оптимизации показал, что согласно принципам
Декарта нецелесообразно рассматривать сразу несколько уровней системы. Разделение систем
на уровни называется принципом декомпозиции, который позволяет упростить задачу
оптимизации систем. А если технические параметры системы какого-либо уровня совпадают с
показателями качества системы более низкого уровня, возможно использовать обратный
принцип интеграции, агрегирования. Во всяком случае более высокому иерархическому уровню
системы соответствует более общие, более абстрактные показатели качества. На высших
иерархических уровнях больше сказывается влияние человеческого фактора даже для
автоматизированных систем.
Глядя на иерархическую структуру систем, может сложиться впечатление, что
экономическая эффективность системных задач с ростом уровня системы возрастает. Однако
это не всегда так, поскольку число малых систем, подсистем значительно больше, чем систем
высокого уровня. Поэтому прикладная наука, обслуживающая системы низкого уровня могут
