Алешин Г.В., Богданов Ю.А. Эффективность сложных радио-технических систем
Подождите немного. Документ загружается.

31
2.3. Об оптимальном соотношении между шириной диаграммы направленности антенны и
дисперсией погрешности углового сопровождения
В предположении нормальности распределения погрешности сопровождения по каждому
углу и нормальности формы диаграммы направленности в главном лепестке получено
распределение и моменты уровня сигнала при угловых флуктуациях диаграммы направленности
в режиме сопровождения по углам. Зависимость средней мощности от отношения ширины
диаграммы направленности антенны к среднеквадратичной погрешности углового
сопровождения сказывается на величине максимальной дальности радиолинии. В данном
подразделе определяется оптимум по типу насыщения для указанного отношения.
Вопрос о влиянии флуктуаций антенны по углам на среднюю мощность сигнала и вопрос об
определении оптимального соотношения между шириной диаграммы направленности по
мощности и дисперсией флуктуаций по углам особенно остро стоит при создании систем с
протяженными радиолиниями, использующих сигналы большой длительности и применяющих
антенны с большим КНД.
Необходимость обеспечения заданного энергетического потенциала радиолинии требует
увеличения КНД применяемых антенн, а, следовательно, предъявляет более жесткие требования
к точности систем угловой стабилизации или сопровождения по углам.
Для простоты рассмотрим одностороннюю радиолинию, у которой антенна идеально
стабилизирована по одному и имеет конечную дисперсию погрешности углового сопровождения
D
x
по другому углу
Θ
x
, которой характеризуется система угловой стабилизации.
В режиме автосопровождения по углу
Θ
x
обычно
D
x x
< ∆Θ
, где
∆Θ
x
— квадрат ширины
ДН антенны по полю на уровне 0,607.
Для этого случая в окрестности максимума хорошей аппроксимацией диаграммы
направленности
G
x
( )Θ
по полю в плоскости
Θ
x
реальных остронаправленных антенн может
быть
G
x
x
x
( ) expΘ
Θ
∆Θ
= −
2
2
. (2.3.1)
В случае автосопровождения по углу ввиду многопричинности возмущений и большой
постоянной времени системы стабилизации по углу отклонения
Θ
x
t( )
максимум ДН от
направления на цель есть случайный центрированный стационарный в узком смысле и
коррелированный процесс в каждом сечении времени
p
D
D
x
x
x
x
( ) expΘ
Θ
= −
1
2
2
2
π
. (2.3.2)
Определим распределение уровня сигнала по полю
p G( )
p G p
G
x
x
( ) ( )= ×2 Θ
∂Θ
∂
. (2.3.3)
Поскольку
Θ ∆Θ
x x
G
= 2
1
ln
, (2.3.4)
то
p G
G
G
( )
ln
=
−
α
π
α 1
1
. (2.3.5)
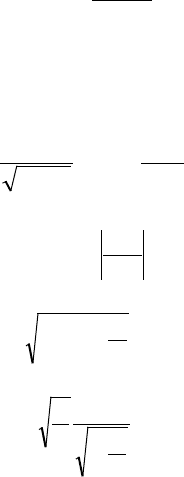
Семейство
p G( , )α
представлено на рис. 2.3.1.
32
Отсюда математическое ожидание
M[G] =
+
α
α 1
, (2.3.6)
а n - ый начальный момент
M
n
n
[G ]=
+
α
α
. (2.3.7)
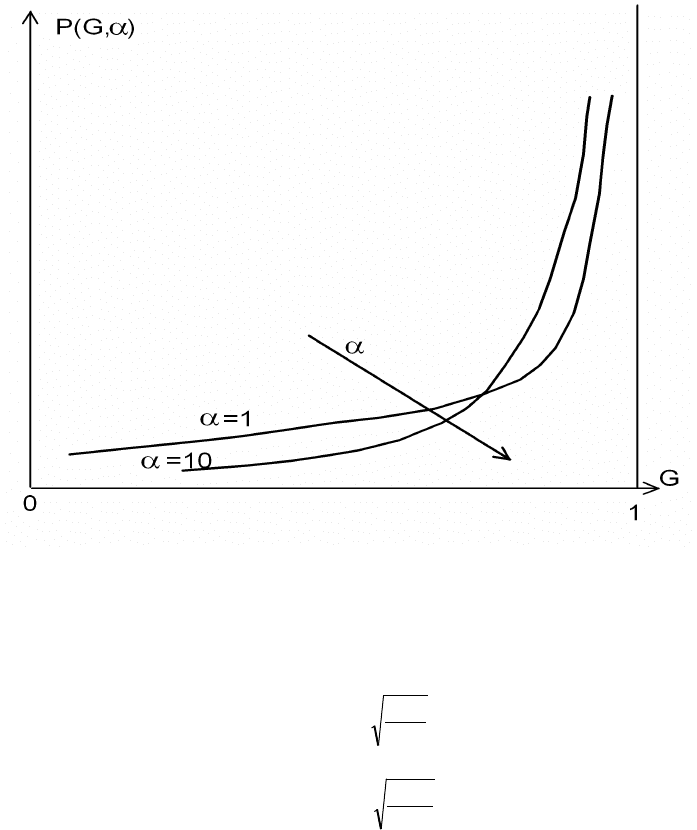
Зависимости
M[G]
и
M[G ]
2
представлены на рис. 2.3.2. Из выражений (2.3.6, 2.3.7), а
качественно также из рис. 2.3.2 видно, что учет дестабилизирующих факторов не излишний уже
при
α ≤ 8
, а при
α ≅ 1
он просто необходим, поскольку при
α = 8
средние энергетические
потери составляют 10 %, а при
α = 1
— 50 %. Очевидно, что с уменьшением
α
растет роль
мультипликативных помех, имеющих распределение (2.3.5).
На больших дальностях, когда и возможности оптимальной обработки сигнала исчерпаны, и
используется максимально достижимая мощность передатчика, требуется увеличение КНД
антенны (уменьшение
∆Θ
x
,
∆Θ
y
).
Тогда необходимо предъявлять более жесткие требования к системе пространственной
стабилизации ДН антенны. Точность отслеживания механической части системы и допуски на
флуктуацию ДН также определяются выражениями (2.3.6, 2.3.7).
При увеличении КНД усложняется и утяжеляется поворотная часть, растет время
корреляции флуктуаций за счет инерционности системы. Однако время корреляции флуктуаций
по углам определяет характер оптимальной обработки сигнала, но не средние энергетические
потери, определяемые за более продолжительный промежуток времени.
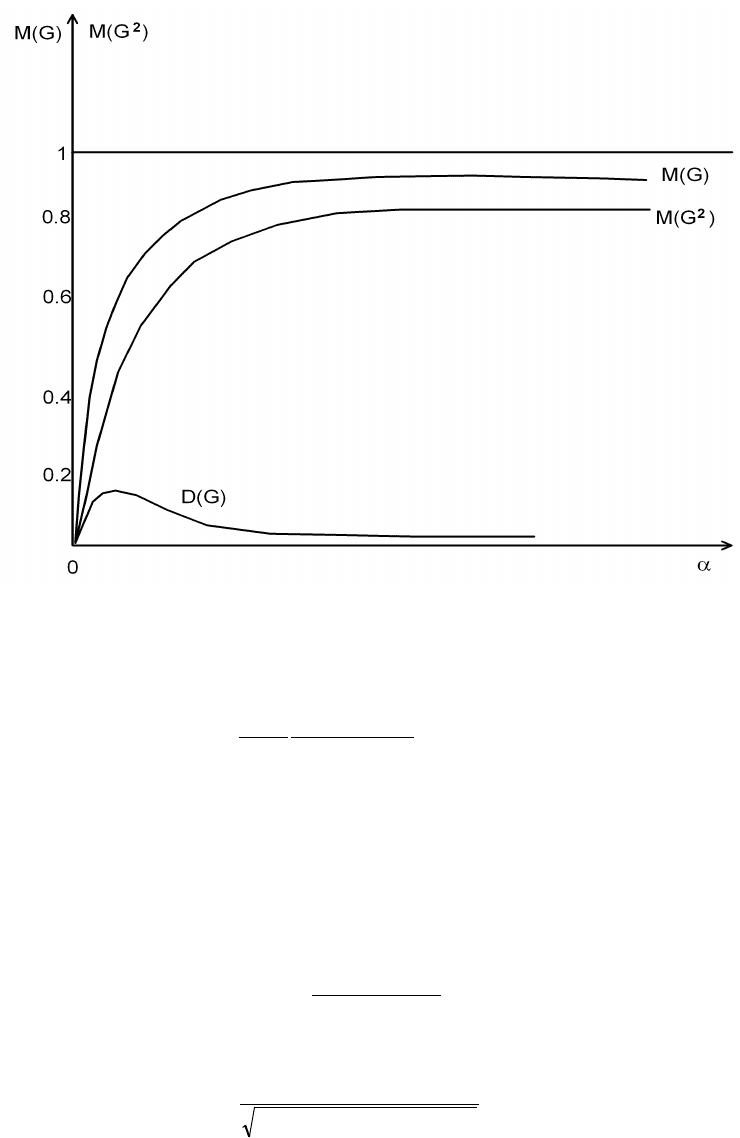
Максимальная дальность радиолинии
r
max
с учетом угловых флуктуаций при заданном
энергетическом потенциале и параметрах радиолинии может существенно зависеть от параметра
α
.
Рис 2.3.1
33
Для указанной модели односторонней радиолинии
[ ]
r
P
P
G G
M G
п д
с прм
п дmax
р
р
2
0 0
2
2
2
16
=
прд прм
λ
π
, (2.3.8)
где
P
п др
— мощность передатчика,
P
с прм
— реальная чувствительность приемника,
G
0 прд
— КНД передающей антенны,
G
0 прм
— КНД приемной антенны,
λ
— длина волны.
Поскольку КНД антенны (
G
0 прд
) можно представить в виде
G
K
x прд y прд
0
1
прд
=
∆Θ ∆Θ
(2.3.9)
для остронаправленных антенн, выражение (2.3.8) с учетом (2.3.9) можно записать
следующим образом (рис. 2.3.3)
r
K
D
x прд x прд x прд
max
( )
2
2
2
=
+∆Θ ∆Θ
, (2.3.10)
где
K
1
,
K
2
— постоянные,
∆Θ
x прд
,
∆Θ
y прд
— как и прежде, квадрат ширины диаграммы направленности передающей
антенны на уровне 0,607 в плоскостях неидеально и идеально стабилизированных углов
соответственно.
Рис 2.3.2
34
Из (2.3.10) следует, что зависимость
r
max
2
от
D
x прд
, т. е.
∂
∂
( )
( )
( ) ( )
max
r
K D D
x прд
x прд x прд x прд x прд x прд
2
2
3 2
2
∆Θ
∆Θ ∆Θ ∆Θ= − + +
−2
,
∂
∂
( )
( )
( )
max
r
D
K D
x прд
x прд x прд x прд x прд
2
2
3 2
2= − +
−
∆Θ ∆Θ ∆Θ
2
и
∂
∂∆Θ
( )
max
r
x прд
2
всегда >
∂
∂
( )
max
r
D
x прд
2
,
для любых
D
x прд
и
∆Θ
x прд
. Следовательно, имеет смысл для увеличения дальности
действия радиолинии преимущественно уменьшать ширину ДН антенны по сравнению со
среднеквадратической погрешностью стабилизации по углу. Это легко увидеть, если переписать
(2.3.10) в виде
r
K
x прд
max
2
2
1
2
=
+∆Θ
α
. (2.3.11)
Ясно, что целесообразность использования отношения
α
большего 8 уменьшается, т. к.
дальнейшее уменьшение
D
x
мало сказывается на увеличении
r
max
2
. При
α ≥ 8
потери
энергетического потенциала
1
2
− M[G ]
составляют согласно (2.3.7)
≤
11 %.
Все изложенное нетрудно распространить на реальные радиолинии, где угловые флуктуации
ДН антенн происходят независимо по двум углам на двух концах радиолинии. В этом случае
среднее значение
r
max
2
зависит от
M
i i
i
[G ( )]∆Θ
=
∏
1
4
для односторонней радиолинии и среднее
значение
r
max
4
зависит от
M
i i
i
[G ( )]∆Θ
=
∏
1
8
для радиолиний с ретранслированным активным
ответом.
Рис 2.3.3.

35
Если антенна используется, кроме того, для пеленгации цели амплитудным или
моноимпульсным методами, то
D
x
и
α
определяются из условия обеспечения необходимой
точности измерения угла.
Однако, и при этом возможен случай соизмеримости
D
x
и
∆Θ
x
, откуда вытекает
необходимость учитывать потери энергетического потенциала.
2.4. Оптимизация параметров дискриминаторных измерений
Под дискриминаторным, или функциональным, измерителем понимается любая
параметрозависимая цепь (или устройство), у которой выходной параметр индикации зависит от
значения измеряемого параметра. Параметром индикации чаще всего бывает напряжение,
цифровое значение параметра, отклонение или угол отклонения стрелки, луча осциллографа и т.
п. Практически все сложные методы оценивания параметров сигнала содержат как составную
часть дискриминаторные измерители. Методы оценивания параметров сигнала можно
классифицировать следующим образом:
1) дискриминаторные измерители, следящие и неследящие;
2) поисковые, или панорамные измерители;
3) многоканальные измерители;
4) многошкальные измерители с параллельными и последовательными шкалами;
5) многоэтапные измерители;
6) комбинированные измерители.
В поисковых и многоканальных измерителях процессы обнаружения сигнала и измерения
его параметра обычно совмещены. В других измерителях предполагается предварительное
обнаружение (возможно, различение) сигнала.
Под измеряемыми параметрами сигнала понимаются как параметры его селекции, или
различения его на фоне других сигналов и помех, так и другие его параметры. Параметрами
селекции могут быть: время t, фаза
ϕ( )t
, несущая частота
f t
0
( )
, или частоты модуляции
F t
i
( )
,
поляризация ж(t), уровень сигнала
U t
c
( )
, структура сигнала
u t
c
( )
или поля
E t
c
( )
,
характеристики диаграмм направленности антенн G и т. п.
Все измерители в радиотехнических системах обладают той особенностью, что они
предназначены для работы с сигналами сравнительно малых уровней и с соизмеримыми на
входе шумами. Поэтому вопросам фильтрации сигналов в шумах уделяется особое внимание.
Фильтрация относится к этапу измерительных преобразований, а роль измерительных устройств
— сравнение параметра сигнала с некоторыми эталонными параметрами, в качестве которых
чаще бывает либо настройка шкал либо вся дискриминаторная характеристика.
В данном разделе будут рассмотрена эффективность дискриминаторных измерителей.
Поскольку приведенная классификация измерителей по методам оценивания может
оказаться необычной, как и следующие разделы, посвященные сложным измерителям, заметим,
что старую теорию оценивания параметров сигналов следует признать некорректной. Поэтому
основные идеи, постулаты старой теории измерений и идеи новой измерительной идеологии
приведены в следующем подразделе.
2.4.1. Физический смысл метода максимального правдоподобия.
Радиоизмерения обобщают рассмотренные в метрологии методы измерений на случаи,
когда воздействуют на вход радиосистемы помехи, когда имеется широкий диапазон
измеряемых параметров и когда требуется большая оперативность обработки сигнала. Поэтому
наряду с термином «измерение» в радиотехнике используется термин «оценка». В настоящее
время существенной разницы между ними при этом не ощущается.
Рассмотрим физическую сущность метода максимума правдоподобия путем простейших
рассуждений.
Известен [4,6,17 и др.] функционал бесконечномерной плотности распределения
вероятности
p n t( ( ))
гауссового шума на отрезке времени от 0 до T
p n t K
N
n t dt
n
T
( ( )) exp ( )= −
∫
1
0
2
0
, (2.4.1)
где
K const
n
=
.

36
На вход радиоприемного устройства подается смесь
y t( )
сигнала
S t
n
( , )λ
с шумом
n t( )
y t S t n t
n
( ) ( ,
) ( )= +λ
, (2.4.2)
где
λ
n
— истинное неизвестное значение параметра
λ
.
Вместо флуктуационного шума
n t( )
в выражение (2.4.1) подставляется его значение из
выражения (2.4.2).
Тогда получим
p y t K
N
y t S t dt
n n
T
[ , ( )] exp [ ( ) ( , )]λ λ= − −
∫
1
0
2
0
. (2.4.3)
Ввиду справедливости выражения (2.4.2) функционал (2.4.3), как и (2.4.1) не зависит от
S t
n
( , )λ
.
Метод максимума функционала правдоподобия предполагает известными реализацию
y t( )
и форму сигнала
S t
n
( , )λ
. В качестве оценки измеряемого параметра
λ
n
принимается такое
значение
λ
n
, при котором функционал (2.4.3) достигает максимума. Согласно этому методу,
ввиду наличия лишь одной реализации
y t( )
, уравнение правдоподобия представляет собой
простое равенство
S t y t
n
( ,
) ( )λ =
, (2.4.4)
где
λ
n
— оценка параметра
λ
n
по одной реализации
y t( )
.
Физическую сущность метода максимума функционала правдоподобия покажем на простом
примере, когда
y S n
n1 1 1
= +
в одном сечении времени
t
1
указанных процессов. В этом случае
y y t
1 1
= ( )
— результат измерений, т. е. оценка сигнала
S S t
n n
1 1
= ( , )
λ
при истинном значении
параметра
λ
n
, а
n n t
1 1
= ( )
— гауссова флуктуационная помеха в момент
t
1
, которая и привела к
погрешности в оценке сигнала. Если бы значение
S
n1
и дисперсия помехи были известны, что
обычно имеет место, то можно было бы плотность распределения реализаций
y y t
1 1
= ( )
генеральной
совокупности представить в виде
p y S
n
( )
1 1
−
рис. 2.4.1. Здесь случайной величиной является сама
реализация
y y t
1 1
= ( )
. Но после приема сигнала реализация
y
1
стала известной. Тогда естественно
предположить, что поскольку все возможные реализации, и
y
1
в том числе, уклоняются по
гауссовому закону относительно истинного значения
S
n1
, то значит и наоборот, истинное значение
неизвестного для нас измеряемого параметра
λ
точно таким же образом, только неизвестно, в какую
сторону, уклоняется от реализации
y
1
. То есть, закон распределения измеряемого сигнала
S S t
n n
1 1
= ( , )
λ
с измеряемым параметром
λ
n
есть
p S y p y S
n n
( ) ( )
1 1 1 1
− = −
, поскольку распределение
симметрично (рис. 2.4.2). Рассуждения справедливы также для второй реализации
y
1
2( )
, для третьей
—
y
1
3( )
и т. д. По существу
p S y
n
( )
1 1
−
— это распределение истинного значения измеряемого
параметра
λ
n
при условии, что известна реализация
y
1
. Поскольку рассуждения справедливы для
любого наблюдения
y
i
, то результирующая плотность распределения вероятности определяется для
случая совмещения событий, т.е., для имеющихся реализаций
y y
n1
, ,
определяется произведением
условных распределений
p S y
n i
( )
1 1
−
, которое и есть результирующий функционал правдоподобия.
Рассуждения распространяются для всех сечений процессов во времени от 0 до T. Далее
отыскивается такое значение
λ
n
(или
S
n1
), которое доставляет максимум функционалу
правдоподобия (ФП).
.
37
Рис. 2.4.1
Рис 2.4.2
Рис. 2.4.3
38
Рис. 2.4.4.
Следовательно, если отыскивать максимум (2.4.3) при заданном значении
y t( )
, варьируя
λ
n
,
то это и есть максимум ФП.
Опуская известные идеи об измерительных преобразованиях, о фильтрации, о методах
формирования шкал и количественных характеристик, остановимся на этапе сравнения
измеряемых параметров, или их функционалов, с эталонными параметрами.
Сравнение оцениваемых параметров сигналов в радиотехнических системах с эталонным
(более точным) параметром, или шкалой, производится обычно в неследящих дискриминаторах
(различителях), или в функциональных измерителях, где эталонной считается их настройка. В
следящих измерителях принятие решения об измеряемом параметре производится обычно по
соответствующему параметру управляемого генератора, по положению фазового центра
антенны и т. д.
Дискриминатор преобразует сигнал с его измеряемым параметром в параметр индикации в
соответствии с дискриминаторной характеристикой. Чаще всего параметром индикации служит
напряжение, удобное для дальнейших применений, либо цифровое значение параметра.
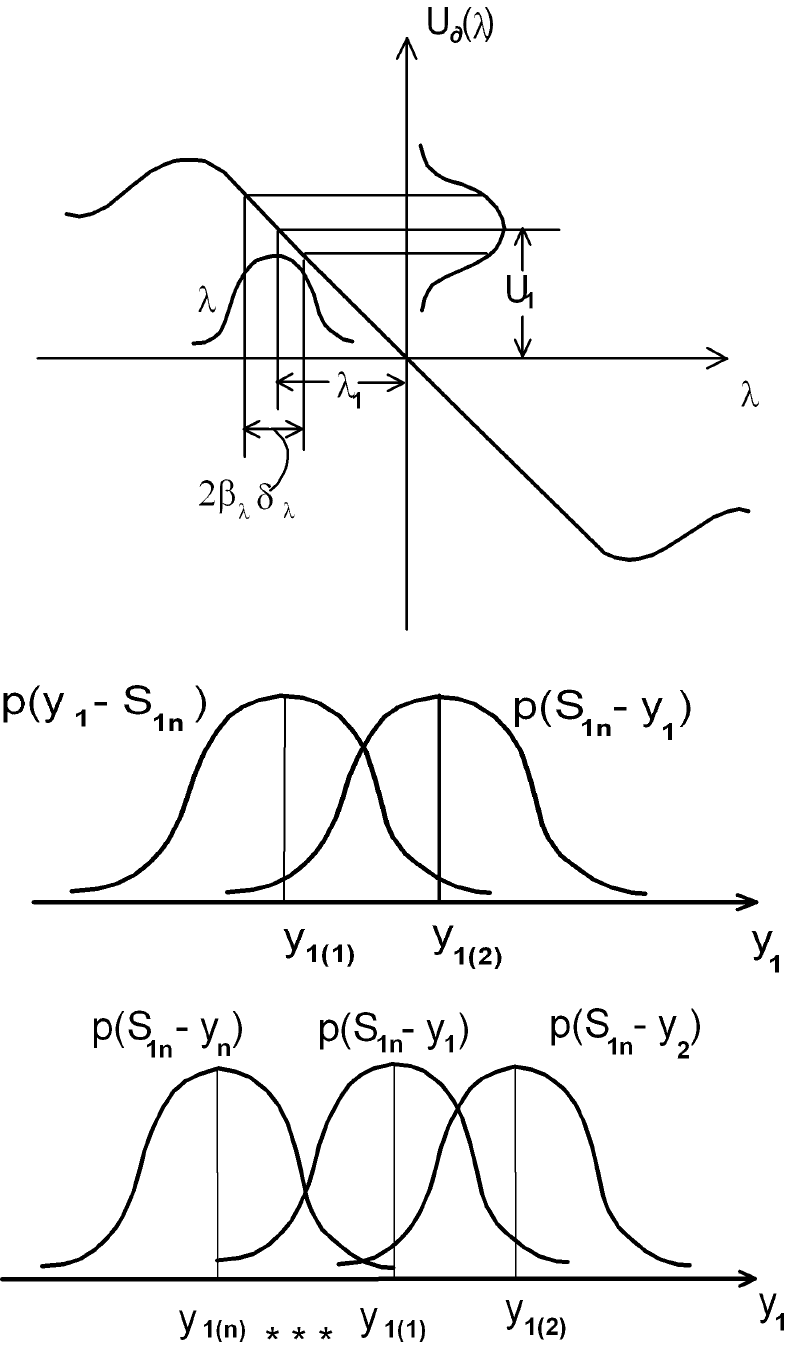
На рис. 2.4.3 представлена дискриминаторная характеристика
U( )λ
с практически
линейным участком.
Шумы и помехи, усиленные и преобразованные, попадают каким-либо образом на выход
дискриминатора и являются источником ошибок в оценке параметра. Если шумы
σ
ш
t( )
на
выходе дискриминатора стационарны и симметричное распределение
p U
U
( )
с математическим
ожиданием
M U( )
, то ему соответствует распределение
p
λ
λ( )
измеряемого параметра
λ
с
математическим ожиданием
M[ ]λ
p d p U dU
Uλ
λ λ( ) ( )=
(2.4.5)
и справедливо
M U U M[ ( )] ( [ ])λ λ=
. (2.4.6)
Тогда справедливо выражение и для дисперсии
σ λ λ λ λ
λш U
U M U p U dU U M U p d
2 2 2
= − = −
∫∫
−∞
∞
−∞
∞
( [ ]) ( ) { ( ) [ ( )]} ( )
. (2.4.7)
Разлагая функцию
U( )λ
в ряд Тейлора в окрестности
M[ ]λ
, подставляя его в выражение
(2.4.7) и принимая во внимание (2.4.6) и малость
′′
U
λ
и других членов ряда Тейлора, получим
σ λ λ λ λ λ
λ λш
U M M p d
2 2 2
=
′
−
∫
−∞
∞
{ ( [ ])} ( [ ]) ( )
.
Отсюда следует, что
σ
σ
λ
λ
2
2
2
=
′
ш
U( )
. (2.4.8)
39
Таким образом, дисперсия
σ
λ
2
оценки параметра
λ
пропорциональна дисперсии шумов на
выходе дискриминатора и обратно пропорциональна квадрату крутизны его характеристики. Это
не очень известный результат. В существующей теории радиоизмерений «потенциальная»
дисперсия оценки параметра обратно пропорциональна второй производной от сигнальной
функции, или от функции автокорреляции, по параметру
λ
. Это справедливо для метода,
использующего релеевское разрешение. А данный результат хорошо согласуется с опытом
эксплуатации систем, с принципами оптимальности зрительного анализатора (раздел 7) и т. д.
Форма сигнала для измерений частоты также отличается от теоретически оптимальной формы.
Например, доплеровский метод оценивания частоты использует гармонический сигнал, а не, так
называемый, оптимальный, т. е. две
δ
-функции, разнесенные по времени, и другое [6, 11, 17].
Из полученного результата следует также, что не обязательно формировать
автокорреляционную функцию для измерений параметра
λ
, особенно если параметр — несущая
частота
f
0
или угловые координаты.
Поэтому соотношение (2.4.8) используем как для формализации зависимости дисперсии
оценки измеряемого параметра
λ
от параметров дискриминатора, так и для изучения основных
свойств этого простейшего измерителя.
Основы нового подхода к измерениям излагаются и далее во втором разделе, однако именно
здесь содержится главная мысль об эффективности принятия решения об измеряемом параметре
в простейшем измерителе.
2.4.2. Системный анализ дискриминаторных измерителей
Основная цель системного анализа — получение, формализация в результате исследований,
зависимости по возможности всех показателей качества систем от технических параметров..
В данном подразделе будем интересоваться, прежде всего, зависимостью показателя
точности, или дисперсии, оценки параметра от параметров дискриминатора.
Существует большое множество параметрозависимых цепей, служащих дискриминаторами.
Однако, согласно соотношению (2.4.8) следует выбирать лишь такие, которые имеют
дискриминаторную характеристику с большой крутизной, что обеспечивает наибольшую
точность
σ
λ
−2
. Например, частотомеры интерференционного типа, где амплитуда суммарного
сигнала медленно изменяется с частотой, для высокоточных измерений частоты непригодны,
хотя и работают в большом диапазоне частот. Для высокоточных измерений частоты обычно
выбираются дискриминаторы, использующие явление резонанса, для углов — диаграмма
направленности (возможно с использованием интерференции, фазовых методов), для измерений
задержки — строб-импульсы, автокорреляционная функция сигнала или фазовые методы и т. д.
Фазовые методы оценивания параметров сигнала самые точные, поскольку крутизна гармоник
велика, особенно на больших частотах. Уровень сигнала также определяет крутизну
дискриминаторной характеристики и, следовательно, его точность. Незнание относительной
погрешности уровня сигнала или его нестабильности допустимы в худшем случае до значения
1 q
, где q — отношение сигнал / шум [21, 22]. Только в этом случае погрешность
дискриминатора за счет нестабильности уровня сигнала не будет превосходить погрешности за
счет действия флуктуационного шума.
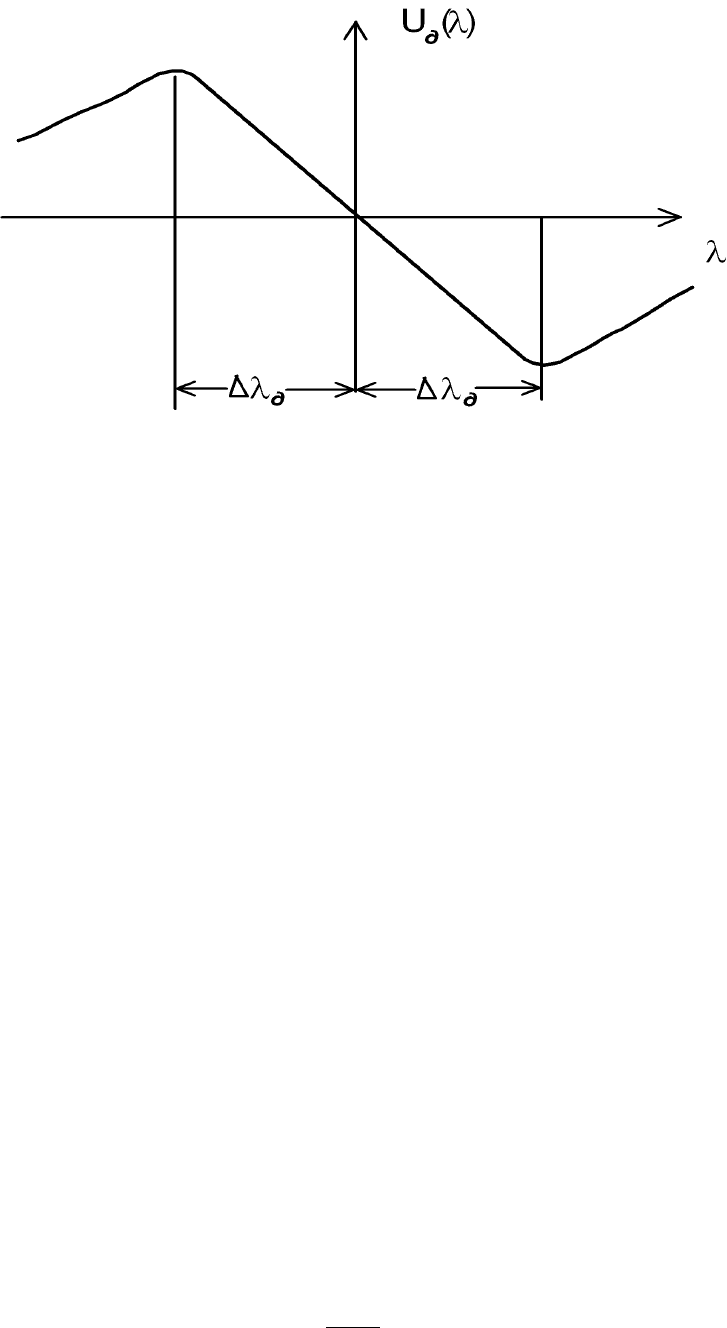
Если рассматривать двухканальный дискриминатор [21,23] с характеристикой
U
∂
λ( )
(рис.
2.4.4), то дисперсия оценки параметра
λ
определяется
σ
λ
λ
∂
2
2
2
=
∆
q
, (2.4.9)
где
2∆λ
∂
— апертура двухканального дискриминатора. Максимальное значение
U
∂
λ( )
определяется амплитудой сигнала. Под апертурой дискриминатора понимается диапазон
однозначного измерения параметра.
Если априорный диапазон есть
∆λ
D
, который равен
∆λ ∆λ
D
= 2
∂
, то формула (2.4.9)
принимает вид
σ
λ
2
2
2
=
∆λ
D
q
.
Двухканальный дискриминатор представляет собой устройство формирования двух
сдвинутых по настройке относительно друг друга каналов (частотных характеристик фильтров,
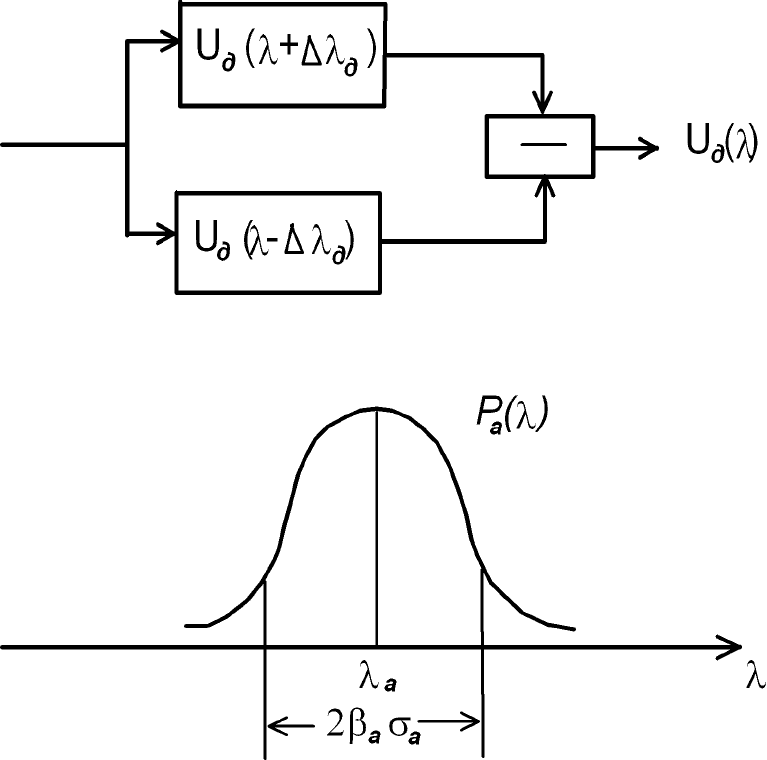
40
диаграмм направленности или автокорреляционных функций и т. п.) (рис. 2.4.5) с вычитающим
устройством. Он обладает лучшей линейностью характеристики, чем у одноканального. Ввиду
этого он используется чаще, чем одноканальный. Его точность
σ
λ
−2
вдвое выше, чем у
одноканального при том же априорном диапазоне
∆λ
D
и при том же отношении сигнал / шум q.
Это естественно, поскольку аппаратуры требуется вдвое больше (два канала + схема вычитания).
При этом предполагалось, что флуктуационные шумы каналов некогерентно суммируются в
вычитающем устройстве.
Определим связь точности измерений
σ
λ
−2
с априорной неопределенностью.
Рис. 2.4.5.
Рис. 2.4.6.
Предположим, что имеется симметричное априорное распределение
p
a
( )λ
(рис. 2.4.6) с
дисперсией
σ
λa
и математическим ожиданием
λ
a
. Тогда доверительный интервал равен
2β σ
a a
,
где измеряемый параметр находится с доверительной вероятностью (коэффициентом доверия):
p p d
a
a a a
a a a
∂
λ β σ
λ β σ
λ λ
λ
λ
=
∫
−
+
( )
, а
β
a
— относительный квантиль.
Бесконечный диапазон измеряемого параметра
λ
, равный
( ,−∞ ∞ )
, мы заменили
ограниченным диапазоном с достаточно высокой доверительной вероятностью того, что
параметр
λ
есть там.
Возможны три случая соотношения
2∆λ
∂
и
2β σ
λ λa a
.
