Алексеев В.В. Физическое и математическое моделирование экосистем

Подождите немного. Документ загружается.

также предположить, что скорость вымирания хищников в

отсут-

ствие жертв пропорциональна численности хищников. Когда обе

популяции

будут

находиться вместе, то в первом приближении

можно считать, что скорость поедания хищником жертв пропор-

циональна

числу их встреч, т. е. произведению числа жертв Ы

на

число хищников N

. Прирост численности хищников также про-

порционален

этой величине, но с меньшим коэффициентом. Таким

образом, получаем систему уравнений

где все коэффициенты положительные и постоянные.

Модель имеет равновесное решение

ж = —; N

= — • (4.2)

По

модели (4.1) доля хищных рыб

уловах

выражается формулой

(4.3)

VjV

(б!

Yr/Y2)

Рис.

4.1. Фазовый

«портрет»

классической

вольтерровской системы «хищник—жертва».

При

уменьшении смертности хищника е

(при отсутствии про-

мысла) доля хищников в

уловах

возрастает, что соответствует

результатам статистического анализа уловов рыб, выполненного

Д'Анкона [163].

Анализ устойчивости состояния равновесия по отношению к ма-

лым возмущениям показал, что особая точка (4.2) является «ней-

трально» устойчивой (типа «центр»), т. е. любые отклонения от

равновесия не

затухают,

но переводят систему в колебательный

режим с амплитудой, зависящей от величины возмущения. Траек-

тории системы на фазовой плоскости (Л^

, N

) имеют вид замкну-

тых кривых, расположенных на различных расстояниях от точки

равновесия (рис. 4.1).

Разделив первое уравнение (4.1) на второе, получим диффе-

ренциальное уравнение для кривой на фазовой плоскости (Л^

, N

(4-4)

Интегрируя это уравнение, получим

где С — постоянная интегрирования.

(4-5)

111

Несложно

показать, что движение точки по фазовой плоскости

будет

происходить только в одну сторону. Для этого удобно сде-

лать замену функций Ы

и N

, перенеся начало координат на

плоскости (N

, N

) в стационарную точку (4.2) и введя затем по-

лярные

координаты

^ ^0. (4.6)

Вместо системы (4.1)

будем

иметь

-£• cos

г)5

—-тр (sin ip) р = —е,р sin

-ф

— е,р

sin

о|>

cos г|>,

(4.7)

-^j-

Sin 1|) + "^ (

C0S

'Ф)

= е

гР

cos

'Ф

sin

COS

*•

Умножив первое уравнение на sinij), а второе — на cos гр и

сложив, получим

^ cos

o|>(l +psini|)) + e,sin

i|)(l

COS

^)-

(4-8)

После

аналогичных алгебраических преобразований получим урав-

нение

для р:

-^- = sin т|) (cos т|з) р (е

— е,) — р

sin

1|)

(e, cos

-ф

— е

sin

я|>).

(4.9)

Величина

d^/dt,

как видно из (4.9), всегда больше нуля. Таким

образом,

dtyfdt

не меняет знака, и вращение все время идет

одну сторону.

Интегрируя (4.9), находим период

= [ 24 (4 10)

1 е

cos

i|>(l+p sin i|>) + e,sin

i|>(l+p simp) '

V ;

Когда р мало, то уравнения (4.8) и (4.9) переходят в уравнения

эллипса.

Период обращения в этом

случае

равен

2л

2jt

/4 1П

Таким

образом, малые флюктуации изохронны.

Исходя из периодичности решений уравнений (4.1), можно по-

лучить некоторые следствия. Представим для этого (4.1) в виде

112

проинтегрируем по периоду:

to+T

dt,

(4-13)

Njf

=-г

Т + у

J N

dt.

Так

как подстановки от \gN

и \gN

в силу периодичности об-

ращаются в нуль, средние по периоду оказываются равными ста-

ционарным

состояниям:

( N

dt =

•*!•,

4- i

Л=

—.

(4.14)

J Yi T * Y2

•о

'о

Простейшие

уравнения модели «хищник—жертва» (4.1) обла-

дают

рядом существенных недостатков. Так, в них предполагается

неограниченность пищевых ресурсов для жертвы и неограничен-

ный

рост хищника, что противоречит экспериментальным данным.

Кроме

того, как видно из рис. 4.1, ни одна из фазовых кривых

не

выделена с точки зрения устойчивости. При наличии

даже

не-

больших возмущающих воздействий траектория системы

будет

все дальше

уходить

от положения равновесия, амплитуда колеба-

ний

расти, и система достаточно быстро разрушится.

Несмотря

на недостатки модели (4.1), представления о

прин-

ципиально

колебательном характере динамики системы «хищник—

жертва»

получили широкое распространение в экологии. Взаимо-

действиями «хищник—жертва» объясняли такие явления, как ко-

лебания

численности хищных и мирных животных в промысловых

зонах, колебания в популяциях рыб, насекомых и т. д. На самом

деле

колебания численности

могут

быть обусловлены и другими

причинами.

Так,

при рассмотрении организмов с выраженной возрастной

структурой большое значение имеют эффекты запаздывания, кото-

рые,

как

будет

показано ниже,

даже

в отдельной популяции

могут

вызвать незатухающие колебания. Кроме того, в природных по-

пуляциях нередко решающее значение имеют периодические изме-

нения

факторов внешней среды (температуры, влажности и т. д.).

Рассмотрим,

какие режимы динамики

могут

возникнуть в мо-

дели экосистемы со взаимодействием видов по типу «хищник—

жертва»

при

учете

среды обитания. Наиболее простой в матема-

тическом отношении является система без запаздывания, резуль-

таты моделирования которой можно, кроме того, сравнительно

легко проверить экспериментально, используя сообщества микро-

организмов.

Усложнение модели (4.1)

будем

проводить последо-

вательно с целью выяснения, к каким особенностям динамики

приводит

учет

того или иного фактора.

Важнейшим фактором, который должен учитываться практи-

чески

во

всех

моделях, является ограниченность ресурсов питания

Заказ

№ 57 ЦЗ

для популяций. Рассмотрим систему «хищник —

жертва»

в мо-

дели с замкнутым круговоротом лимитирующего элемента пита-

ния.

Популяция жертвы М

лимитирована в своем росте концент-

рацией элемента в среде, популяция хищника М

— биомассой

популяции жертвы М

- Если не учитывать эффектов, связанных

с насыщением хищника и жертвы, получим систему уравнений

[7, 11, 62]

(4.15)

где е

, е

— коэффициенты смертности жертвы и хищника соот-

ветственно; у, у — коэффициенты соответственно потребления и

усвоения жертвы хищником; р — коэффициент роста жертвы;

— общий запас лимитирующего элемента питания в системе.

Система уравнений

(4.15)

имеет несколько стационарных со-

стояний.

Исследование существования (положительности) стацио-

нарных значений переменных, а также условий устойчивости по

отношению к малым отклонениям от равновесия

дает

следующие

результаты.

Стационарное состояние с нулевыми биомассами жертвы и

хищника (М

= 0, М

= О, S = M

)

существует

при любых зна-

чениях M

> 0, но устойчиво только при M

< Мир, где Mi

/|3. Действительно, рассматривая линеаризованную систему

уравнений для малых отклонений |, переменных от положения

равновесия

^ = М

-М

£, = М

-М

имеем

(4.17)

Решение этой системы |,- = X

CikZ

%kt

зависит от знаков характе-

ристических чисел X, которые можно найти, приравнивая нулю

определитель

-е

рМ

)-^

О -е

- к

(4.18)

Отсюда Х\ = —е

, Ъ

= —е

+ рМ

. Поскольку Х

< 0 при М

< е

/р, в этой области значений параметра M

малые отклоне-

ния

|,- от положения равновесия экспоненциально

затухают

(осо-

114

бая точка типа «устойчивый

узел»).

При М

> е

/Р состояние

равновесия становится неустойчивым.

Рассмотрим также второе состояние равновесия — выживает

только жертва М

= М

— М,

р.

= 0,

(4.19)

= M,

получим, что условие положительности стационарного значения

биомассы жертвы выполняется при M

> Mi

. Анализ устойчи-

вости этой точки равновесия

дает

следующие выражения для ха-

рактеристических чисел к:

= —

р.

(4.20)

При

MIKP

< M

< М

2к

р, где М

2кР

= Мир + г

/у, все А. являются

отрицательными действительными числами и особая точка устой-

чива (устойчивый

«узел»).

При M

> М

2кр

особая точка стано-

вится неустойчивой с экспоненциальным разбеганием траекторий.

Третье состояние равновесия соответствует существованию пол-

ной

системы с хищником и жертвой:

(Mx-M

2Kp

)/(l+

/P),

(4.21)

1+P/Y

Это состояние

существует

при M

> М

2кр

и устойчиво

всюду

области существования. Действительно, в данной области ха-

рактеристическое уравнение имеет вид

Я,

-\-

рМ

Я,

+ Y (Р + у) М

= 0,

(4.22)

откуда

следует,

что все Re

< 0.

Суммируя результаты математического анализа, нетрудно ви-

деть, что ведущим параметром в «развитии» системы от нежизне-

способной

к максимально наполненной видами является общий

запас лимитирующего компонента питания М

. Отметим, что

модели «хищник —

жертва»

без

учета

фактора насыщения неза-

тухающих

колебаний не обнаруживается.

При

возрастании величины M

с какого-то момента, очевидно,

начнет сказываться эффект насыщения организмов по питанию.

учетом

фактора насыщения уравнения

(4.15)

принимают вид

[8,

10, 11]

с?М

.. „ М

Э М

x м

, - М

+ 8 =

8* 115

Здесь все коэффициенты считаются постоянными.

Показано,

что в общем

случае

для

(4.23)

возможны

следую-

щие

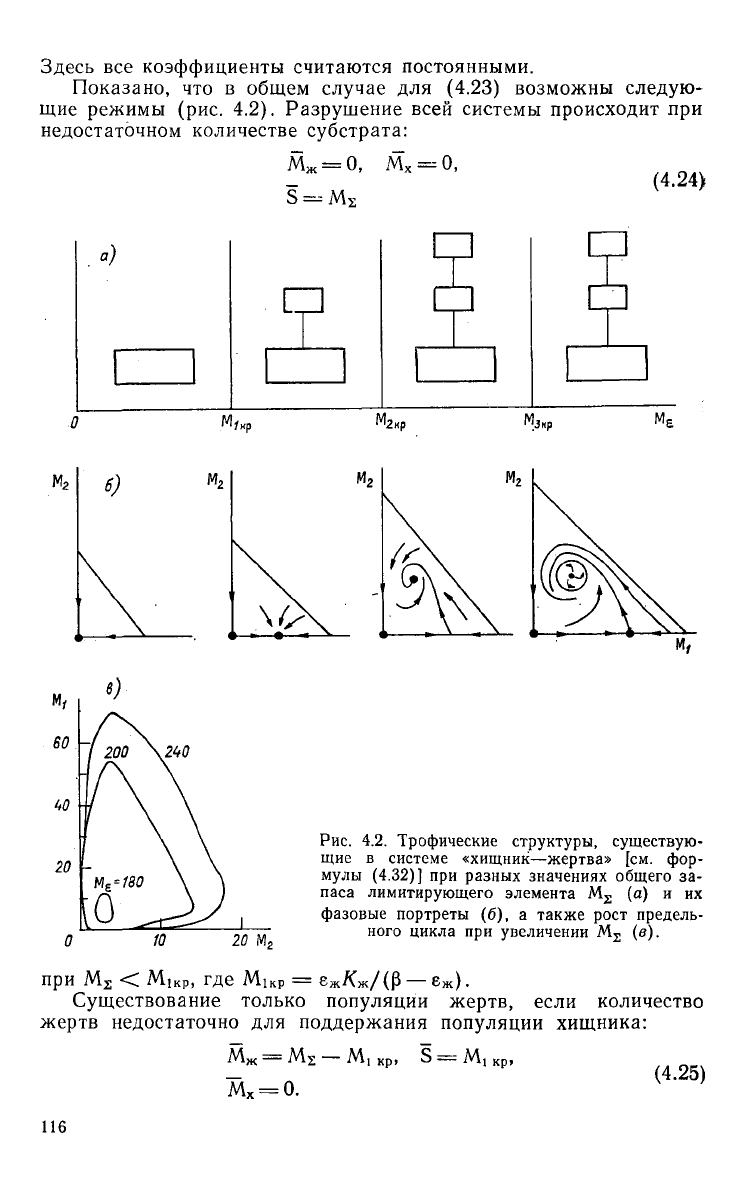
режимы (рис. 4.2). Разрушение всей системы происходит при

недостаточном количестве субстрата:

= 0, М

= 0,

(4.24)

М,

Рис.

4.2. Трофические структуры, существую-

щие

в системе «хищник—жертва» [см. фор-

мулы (4.32)] при разных значениях общего за-

паса

лимитирующего элемента М

(а) и их

фазовые

портреты (б), а также рост предель-

ного

цикла при увеличении М

(в).

при

MIKP,

где

MIKP

= е

/Сж/(Р —е

Существование только популяции жертв, если количество

жертв недостаточно для поддержания популяции хищника:

— М

Кр

S==M

= 0.

(4.25)

116

Этот стационар

существует

при М^ >> М

]кр

и устойчив (особая

точка

«узел»)

при М

< М

2кр

, где М

2кр

= М

1кр

+ ~

• Ана-

логичен стационарному решению

(4.19)

в системе без насыщения.

Существование полной системы «хищник —

жертва».

Стацио-

нарные

значения биомассы выражаются формулами

(4.26)

где

= (M

- М

) + (р - еж)

)/(р - еж) -

Стационарные

значения положительны и определяются единствен-

ным

образом при М

> М

2к

р- Анализ устойчивости по отношению

малым отклонениям

дает

следующее характеристическое урав-

нение

для определения X:

Уравнение

(4.27)

имеет отрицательные Re

Я,

при условии положи-

тельности коэффициента при первой степени X, т. е.

Поскольку

Мх, S изменяются пропорционально М

, очевидно, что

при

возрастании M

, начиная с некоторого

Мзкр,

неравенство

(4.28)

нарушается. На фазовой плоскости (М

, М

) при этом по-

является предельный цикл, возникают незатухающие колебания.

ростом M

предельный цикл растет и подходит в конце концов

достаточно близко к осям координат, что соответствует разруше-

нию

системы.

Экспериментальные работы по изучению систем «хищник—

жертва»

были предприняты Г. Ф.

Гаузе

сразу после появления

печати первых работ В. Вольтерра [48, 194]. Эксперименты

проводились на искусственных экосистемах с использованием изо-

лированных и смешанных

культур

микроорганизмов. Первые

опыты были выполнены с парамецией

Paramecium

caudatum

хищным простейшим

Didinium

nasutum.

В пробирки с 0,5 см

овсяной

среды без осадка, пригодной для развития парамеций,

117

вносили

пять особей P.

caudatum,

а через два дня — три хищника

Didinium.

После внесения хищника к парамециям число послед-

них начинало убывать, хищники интенсивно размножались, по-

едали

всех

парамеций, после чего погибали сами. Этот опыт был

повторен много раз, причем иногда в объемах в несколько литров,

где были сотни тысяч парамеций, хищник вносился в разные

моменты роста популяций, однако всегда получался тот же ре-

зультат.

Вариант опыта на минеральной солевой среде Остер-

гаута,

в которую вносились неразмножающиеся бактерии

Balillus

pyoceyaneus

в качестве пищи для парамеций (с ежедневной сме-

.400 -

tcym

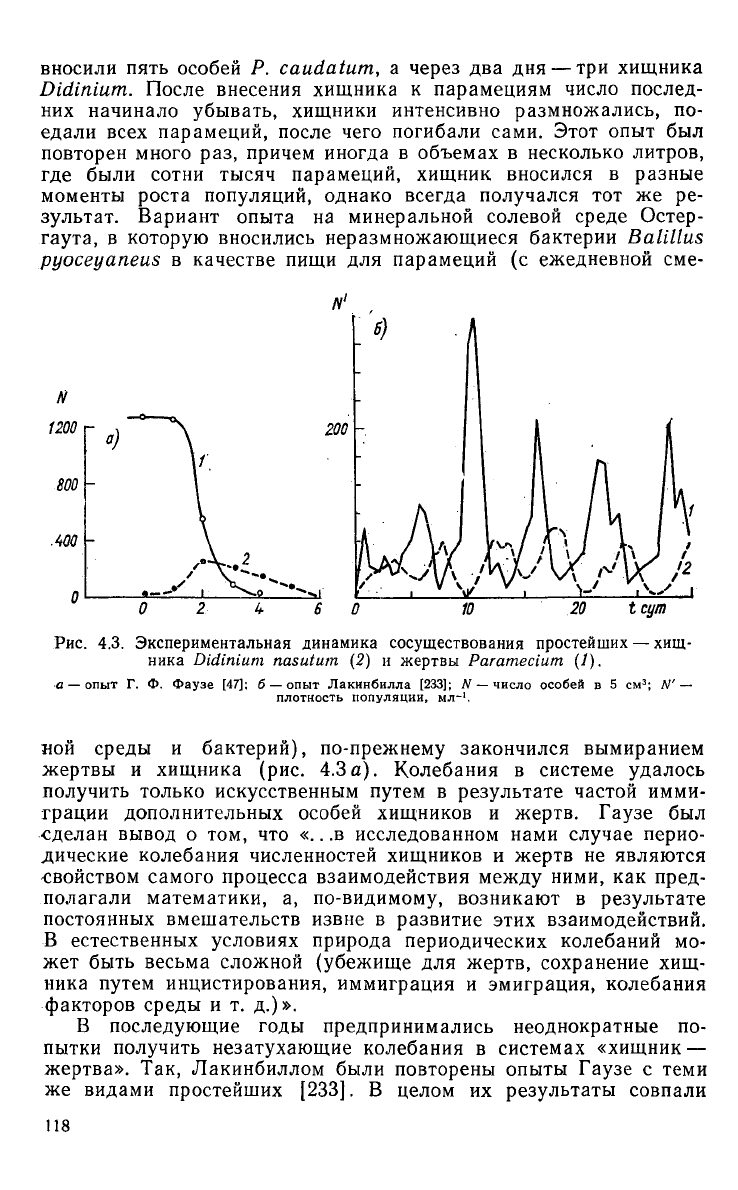
Рис.

4.3. Экспериментальная динамика сосуществования простейших — хищ-

ника

Didinium

nasutum

(2) и жертвы

Paramecium

(1).

•а

— опыт Г. Ф. Фаузе [47]; б — опыт Лакинбилла [233]; N — число особей в 5 см

; N'—

плотность популяции, мл-'.

ной

среды и бактерий), по-прежнему закончился вымиранием

жертвы и хищника (рис. 4.3 а). Колебания в системе удалось

получить только искусственным путем в

результате

частой имми-

грации дополнительных особей хищников и жертв.

Гаузе

был

сделан вывод о том, что «.. .в исследованном нами

случае

перио-

дические колебания численностей хищников и жертв не являются

свойством самого процесса взаимодействия

между

ними, как пред-

полагали математики, а, по-видимому, возникают в

результате

постоянных

вмешательств извне в развитие этих взаимодействий.

В естественных условиях природа периодических колебаний мо-

жет быть весьма сложной (убежище для жертв, сохранение хищ-

ника

путем инцистирования, иммиграция и эмиграция, колебания

факторов

среды и т. д.)».

В последующие годы предпринимались неоднократные по-

пытки

получить незатухающие колебания в системах «хищник —

жертва».

Так, Лакинбиллом были повторены опыты

Гаузе

с теми

же видами простейших [233]. В целом их результаты совпали

118

с выводами Гаузе. Совместное существование хищника и жертвы

удалось продлить путем добавления к среде метилцеллюлозы,

среда при этом становилась вязкой и оба реснитчатых начинали

плавать медленнее, что предохраняло

жертву

от полного выеда-

ния.

Тем не менее в системе происходили колебания численности

с возрастающей амплитудой, приводившие в конце концов к вы-

миранию

хищника. Длительного существования системы в колеба-

тельном режиме удалось добиться, снизив вдвое содержание

культуре

корма для жерт-

вы (см. рис. 4.3 6). Более

мг/мя

детальное рассмотрение про-

цесса показало, что возник-

новение

колебаний обуслов-

лено не собственно пищевым

взаимодействием, а

эффек-

том запаздывания в размно-

жении

хищника Didinium

относительно момента пот-

ребления пищи.

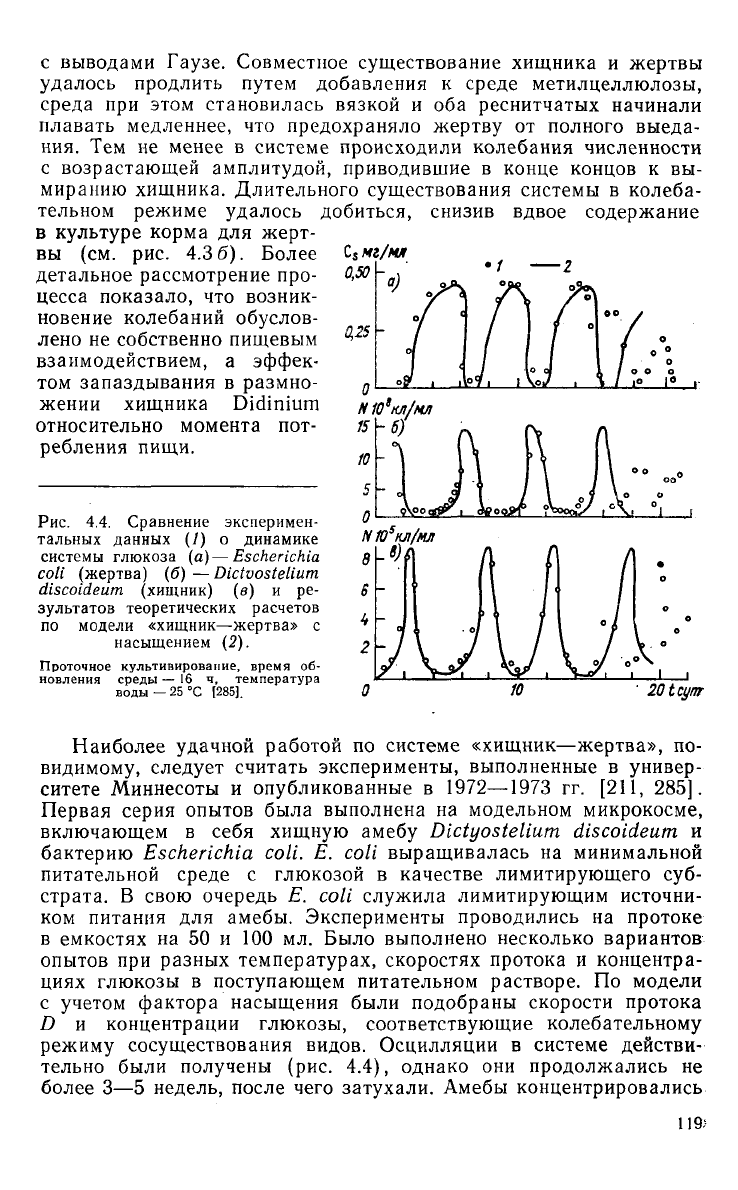
Рис.

4.4. Сравнение эксперимен-

тальных данных (1) о динамике

системы глюкоза

(а)—Escherichia

coli

(жертва) (б) —

Dictvostelium

discoideum

(хищник) (в) и ре-

зультатов

теоретических расчетов

по

модели «хищник—жертва» с

насыщением (2).

Проточное культивирование, время

об-

новления

среды

— 16 ч,

температура

воды-

25 "С

[285].

ZOtcynr

Наиболее удачной работой по системе «хищник—жертва», по-

видимому,

следует

считать эксперименты, выполненные в универ-

ситете Миннесоты и опубликованные в

1972—1973

гг. [211, 285].

Первая

серия опытов была выполнена на модельном микрокосме,

включающем в себя хищную амебу

Dictyostelium

discoideum

бактерию

Escherichia

coli.

coli

выращивалась на минимальной

питательной среде с глюкозой в качестве лимитирующего суб-

страта. В свою очередь Е.

coli

служила лимитирующим источни-

ком

питания для амебы. Эксперименты проводились на протоке

емкостях на 50 и 100 мл. Было выполнено несколько вариантов

опытов при разных температурах, скоростях протока и концентра-

циях

глюкозы в поступающем питательном растворе. По модели

учетом

фактора насыщения были подобраны скорости протока

D и концентрации глюкозы, соответствующие колебательному

режиму сосуществования видов. Осцилляции в системе действи-

тельно были получены (рис. 4.4), однако они продолжались не

более 3—5 недель, после чего затухали.

Амебы

концентрировались

119;

на

стенках

хемостата

вблизи

поверхности

воды

существовали

на

низком

уровне

численности,

а Е.

coli

возвращались

на

перво-

начальный

уровень

высокой

плотностью.

Попытки

реиницииро-

вать

рост

амеб

на

этой

стадии

не

имели

успеха.

Для

анализа

динамики

системы

была

использована

модель

-DC

(4.29)

N10

кл/мл

где С

, С

, Cs —концентрации амеб (хищники), бактерий (жерт-

вы) и глюкозы (лимитирующего субстрата) соответственно; D —

•скорость протока; С* — концентрация глюкозы на

входе

хемо-

стата; a

— коэффициент

потребления глюкозы ба-

ктериями;

аъ —

коэффи-

циент потребления бакте-

рий

ХИЩНИКОМ; Ц,

, ]ХЬ И

Кь, Ks — стандартные обо-

значения

максимальных

скоростей роста и кон-

стант полунасыщения со-

ответственно.

Экспериментальные

значения

коэффициентов

модели приведены в

табл. 4.2. Сравнение мо-

дели и экспериментальных

данных в первые недели

опыта дает хорошее коли-

чественное соответствие

(см.

рис. 4.4). Слабо вы-

раженная нерегулярность

экспериментальных ко-

лебаниях связана, по

Mi/MJ!

N10*

кл/мл

хххх"

16 t cym

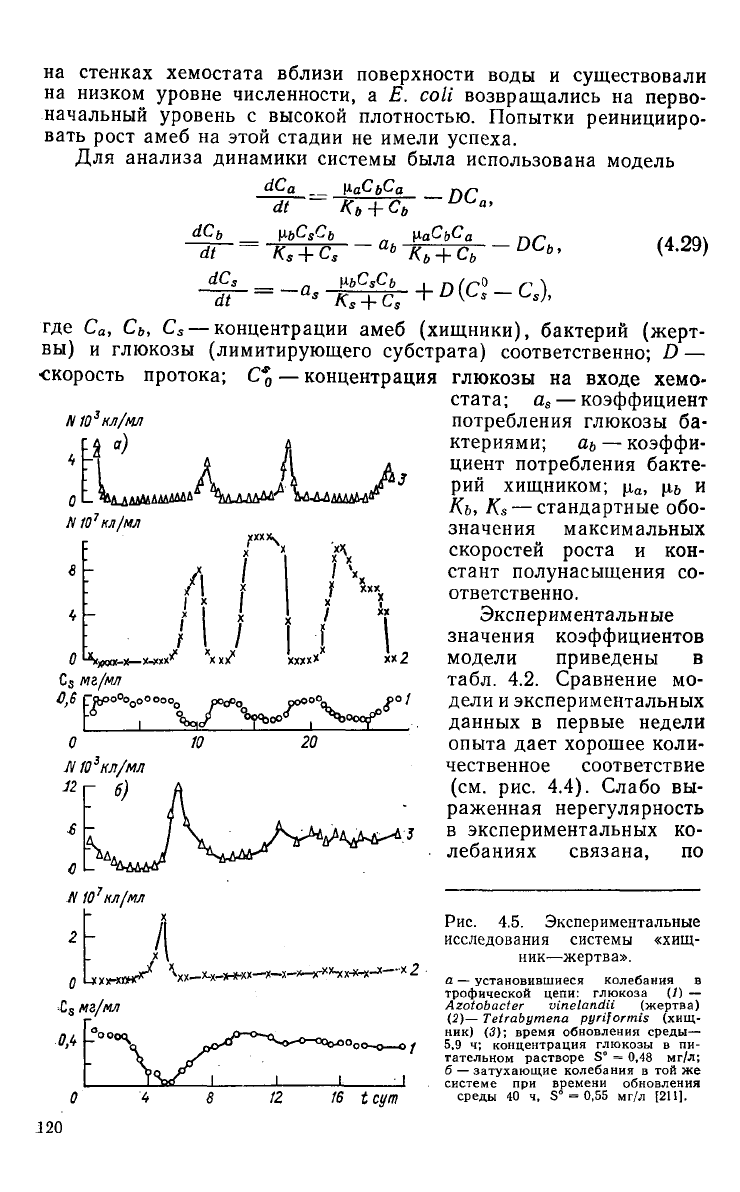
Рис.

4.5. Экспериментальные

исследования системы «хищ-

ник—жертва».

а —

установившиеся

колебания в

трофической цепи:

глюкоза

(Л —

Azotobacter

vinetandii

(жертва)

(2)—

Tetrabymena

pyriformis

(хищ-

ник) (3); время обновления

среды—

5.9 ч; концентрация

глюкозы

в пи-

тательном

растворе

S° = 0,48 мг/л;

б —

затухающие

колебания в той же

системе

при времени обновления

среды

40 ч, S° = 0,55 мг/л

[211].

J20